机载SAR多模式统一化成像处理技术研究

韦 维，朱岱寅，吴 迪

(南京航空航天大学电子信息工程学院雷达成像与微波光子技术教育部重点实验室，江苏南京 211106)

0 引言

合成孔径雷达(Synthetic Aperture Radar,SAR)技术克服了恶劣气象环境的影响，能够实现超视距与高分辨对地观测，从而广泛应用于军事侦察、灾情探测和地形测绘等领域[1-2]。其中，SAR成像技术始终是微波遥感领域的研究热点，且多模式统一化处理占据了高效率监视系统的关键环节。

近年来，美国Sandia国家实验室研发的Mini-SAR(Miniature Synthetic Aperture Radar)，德国FGAN公司的PAMIR等系统均具备多种感兴趣区域(Region of Interest,ROI)探测模式。其中，凝视聚束模式能够最大限度地提升方位向分辨率，而滑动聚束兼具高分辨率与宽测绘带的优势[3]。除此之外，对于SAR实时观测系统而言，多种探测模式下回波数据处理的效率同样重要。因此，需要探索超高分辨SAR多模式统一化处理方法，以便于促进微波遥感技术的高效工程化应用。

超高分辨SAR成像往往面临频谱混叠问题，脉冲重复频率(Pulse Repetition Frequency,PRF)仅会大于瞬时多普勒带宽，而远远小于整个合成孔径内的方位总带宽，过高的PRF容易引起距离模糊。针对上述难题，可分子孔径对混叠信号进行处理，然而分割重组增加了算法复杂性，且拼接误差易导致聚焦质量的恶化[4]。文献[5]利用基于方位向Deramp的两步法(Two Step Approach,TSA)，以恢复混叠频谱为基础，完成了对重建信号的精确聚焦。TSA避免了子孔径拼接及其误差[6-8]，运算效率高，但对斜视信号的处理存在缺陷[5]。此外，在解决频谱混叠问题的前提下，选择恰当的成像算法来进一步满足信号精聚焦的需求同样重要。鉴于此，距离徙动算法(Range Migration Algorithm,RMA)能够满足超高分辨率[9]与宽测绘带的需求。然而，针对大斜视数据处理，信号严重的距离方位耦合使其难以适用。文献[10-11]通过忽略高阶耦合项，实现了2-D近似解耦合和运算量的降低，但其误差限制了大斜视数据的高分辨成像处理。与此同时，线性距离走动校正(Linear Range Walk Correction,LRWC)也是一种有效的斜视信号处理方法[12-13]。文献[14]通过结合LRWC和Keystone变换技术，并利用方位空变的残余距离徙动校正(Range Cell Migration Correction,RCMC)和非线性变标方法，实现了残余高阶RCM校正和多普勒相位均衡。为了进一步改善RMA的自适应性与结合运动补偿的灵活性，文献[15]中扩展型距离徙动算法(Extended Range Migration Algorithm,ERMA)调整Stolt插值以分离方位调制项，能够获得完全校正RCM且方位向未压缩的信号，从而适用于距离空变运动补偿。

综上所述，针对超高分辨机载SAR多模式统一化成像处理技术，需要研究兼具大斜视信号频谱重建与灵活地结合运动补偿的方法，从而实现多模式数据处理的统一性和鲁棒性。据此，本文提出了一种基于扩展型两步法(Extended Two Step Approach,ETSA)与ERMA相结合的多模式统一化成像算法。具体而言，ETSA通过结合TSA与LRWC技术，并以重采样操作转化为无混叠正侧视信号，解决了传统TSA难以恢复斜视信号混叠频谱及其2-D严重耦合的难题。另一方面，精聚焦成像过程RMA难以结合运动补偿算法，ERMA通过修正Stolt插值保留信号的方位多普勒调制特性，从而保证了其与运动补偿相结合的能力。所提方法综合考虑了超高分辨多模式成像的关键技术，能够实现凝视和滑动聚束模式大斜视数据的统一化处理，并结合X波段实测数据处理结果验证了所提方法的有效性。

1 SAR多模式成像模型

本文成像模型针对大斜视凝视和滑动聚束模式。相较于凝视聚束模式，滑动聚束波束旋转中心为地面下方某处的虚拟点。图1所示为多模式成像数据采集模型，ROI#1和ROI#2分别为滑动和凝视聚束模式波束扫描区域，显然前者成像场景较大而后者在积累较多脉冲时方位向分辨率更高。SAR实时观测系统根据不同的对地观测需求切换不同工作模式，统一化的成像处理极具工程化实用价值。图1中，θs和va分别为斜视角与载机飞行速度，R0和Rrot分别为最短斜距及虚拟旋转点到雷达航迹的距离。

图1 滑动聚束和凝视聚束模式几何模型

经调制解调与距离向快速傅里叶变换(Fast Fourier Transform,FFT)，在ROI#1和#2中，点目标P的回波信号形式均可表示为

(1)

式中，C′为常数，fc为载频，c为光速，Kr为距离向调频率，tc为等效波束中心时刻，fr和ta分别为距离向频率和慢时间，Wr和wa分别为距离向频谱包络与方位向信号包络。以凝视聚束模式为例，此时雷达与点目标P之间的瞬时斜距为

(2)

2 统一化成像处理技术

统一化成像处理技术首先需解决超高分辨下的斜视信号频谱混叠以及严重耦合的问题，此外，为实现高效的工程化应用，需要扩展RMA以灵活地结合运动补偿算法。

2.1 频谱重建与信号耦合削弱

本文利用扩展型TSA重建非混叠的频谱。传统TSA核心是利用方位Deramp技术降低多普勒带宽：

exp(j2πKreftat′a)dta

(3)

式中，S(fr,ta)和S′(fr,t′a)分别为原始方位谱混叠信号及卷积后的信号。tr和t′a为快时间与重建信号的慢时间，Kref为参考距离处的方位向调频率。

传统TSA通过增大多普勒频率单元解决正侧视信号矩形频谱的混叠问题。然而，该算法忽视了斜视信号频谱倾斜引起的方位向带宽。为此，本文首先对信号进行LRWC处理，减小信号的两维耦合并且压缩多普勒带宽，然后结合传统TSA实现矩形频谱的重建。LRWC可从以下两方面解释：

1) 瞬时斜距R(ta)在tc处可展开为

(4)

(5)

此时如图2所示，LRWC将信号每一距离门处的多普勒频率中心都搬移到零频处，降低信号方位向带宽以减少重建信号的数据量，可提高工程化应用的计算效率。

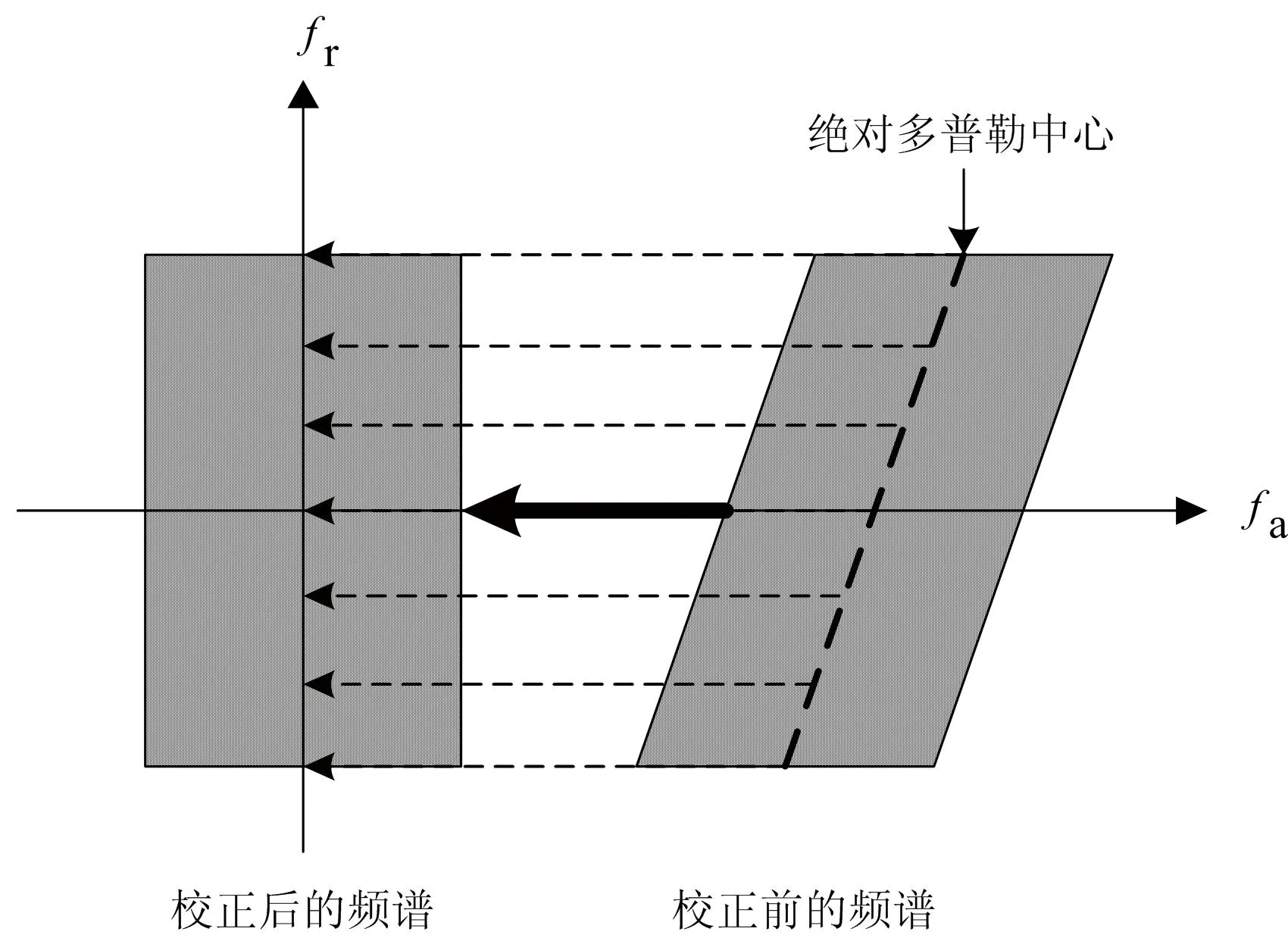
图2 线性距离走动校正效果

LRWC后信号的两维频谱为

(6)

式中，fa为多普勒频率，Wa为方位频谱包络。

然而，直接应用LRWC会导致信号的方位移不变特性失效。经过LRWC处理，目标距离向包络会发生方位空变的移位，使得最短斜距不同的点目标最终出现在同一距离门内且信号发生距离向缠绕。为此，依据文献[16]所提方法对LRWC后的波数域频谱进行方位重采样：

(7)

式中，f′a为重采样后的多普勒频率，经sinc插值后信号形式为

Sresample(fr,f′a)=Wr(fr)Wa(f′a)×

(8)

2.2 扩展的距离徙动算法

传统RMA通过一致压缩完成参考距离处信号的完全聚焦，利用Stolt插值实现距离方位解耦合，完成非参考距离处信号的聚焦。然而，Stolt插值处理后的信号难以结合距离空变运动补偿算法。为此，对Stolt插值进行修正。传统Stolt插值表示为

(9)

从上式中分离出多普勒调制项，可获得修正的Stolt插值：

(10)

经上式处理得到的信号相位为

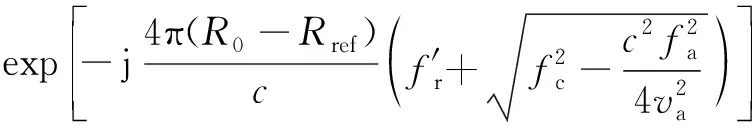
(11)

此时，可利用上述信号结合azimuth scaling等算法进行运动补偿。然后，利用式(12)在距离多普勒域对信号进行补偿，并将其变换至两维时域能够实现成像。此外，也可按式(13)在距离多普勒域成像。

(12)

(13)

式中，Ka为方位向调频率。

上述公式中凝视聚束下的R0均可等效为滑动聚束模式下的Rrot。综上所述，本文所提多模式统一化成像处理方案可以归结为图3所示流程图。处理流程主要包括5部分：

1) 线性距离走动校正，削弱了斜视信号的距离方位耦合。

2) 基于方位Deramp处理的频谱重建方法，解决了信号的频谱混叠问题。

3) 方位向重采样，解决了LRWC后的方位移不变特性失效问题。

4) ERMA实现了对信号的精确聚焦，并保留方位多普勒调制以结合运动补偿算法。

5) 方位Deramp处理，避开了时域缠绕问题在频域实现成像。

上述处理流程综合考虑了多模式数据统一化成像时的若干问题，所提算法能够自适应地处理凝视聚束和滑动聚束大斜视角数据。

3 仿真及实测数据处理

3.1 点目标仿真

为了验证本文所提算法的有效性与可靠性，仿真产生斜视角为45°的聚束模式回波。主要参数如表1所示，可知在此仿真参数下回波在方位频域是混叠的。点目标分布几何模型如图4所示。

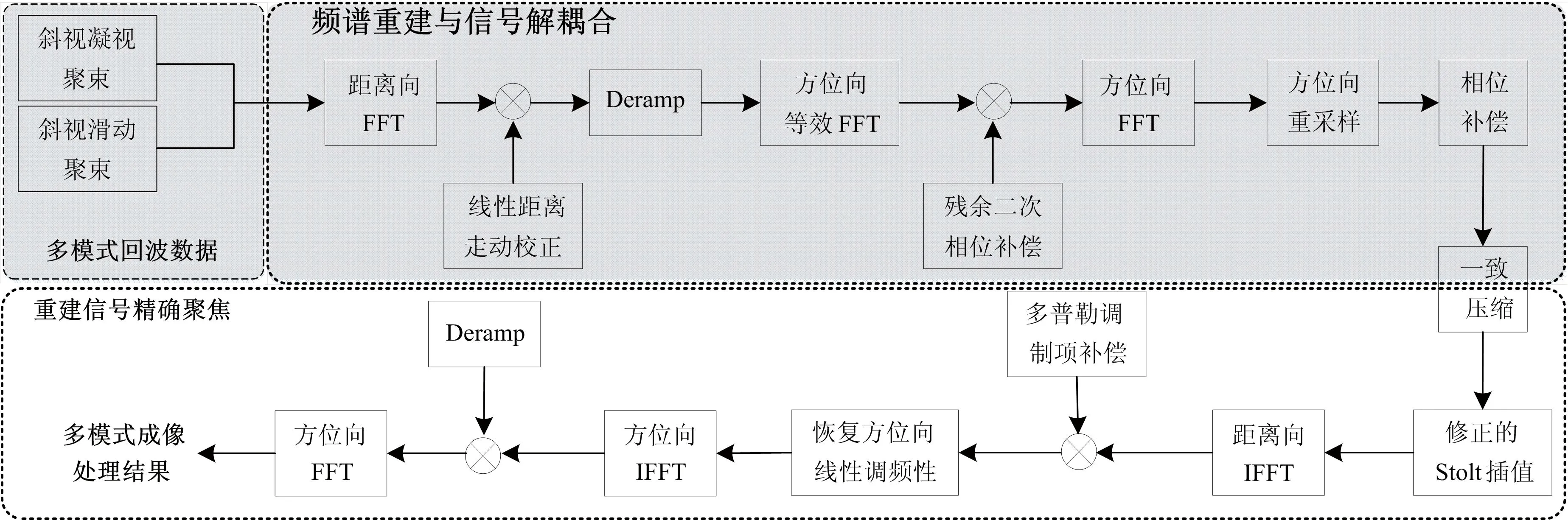
图3 超高分辨率多模式统一化成像处理算法流程

表1 多模式仿真参数

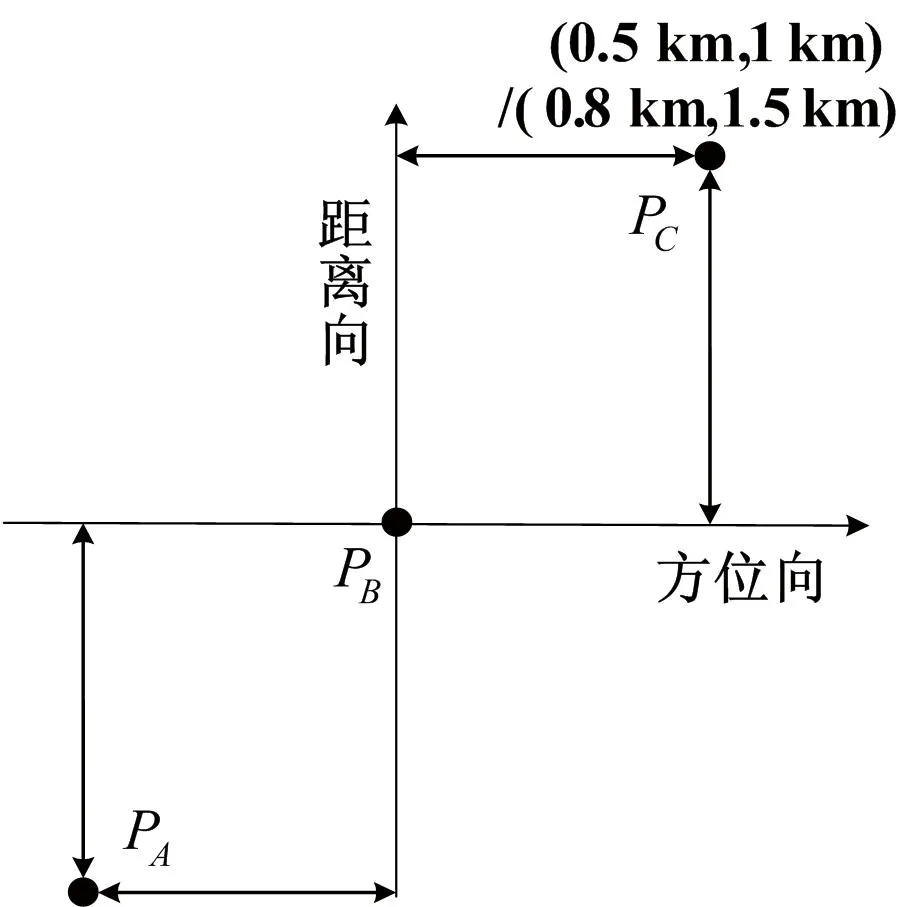
图4 点目标分布几何模型

图5～图7分别为凝视聚束模式下点目标A、B、C的回波经处理后的脉冲响应函数(Impulse Response Function,IRF)等高线和两维的剖面。图8为滑动聚束模式下相应的IRF等高线图。表2给出了点目标IRF峰值旁瓣比(Peak Sidelobe Ratio,PSLR)、积分旁瓣比(Integrated Sidelobe Ratio,ISLR)和冲激响应宽度(Impulse Response Width,IRW)。由剖面图及三种聚焦性能指标可知，多模式SAR信号最终被转化为理想的两维sinc函数。针对单个目标进行分析如边缘点A，距离向与方位向的PSLR都达到理想值-13 dB，在成像时，强散射目标A难以覆盖其相邻的弱目标。与此同时，两维的ISLR同样接近理论值，聚焦后暗回波区域在邻近的强散射区域干扰下，仍可被清晰观测。最后，两种模式下IRF的距离向和方位向的IRW与仿真设定的理论分辨率相符。

(a) 目标A (b) 目标B(c) 目标C图5 点目标IRF等高线图

(a) 目标A (b) 目标B(c) 目标C图6 点目标IRF距离向剖面

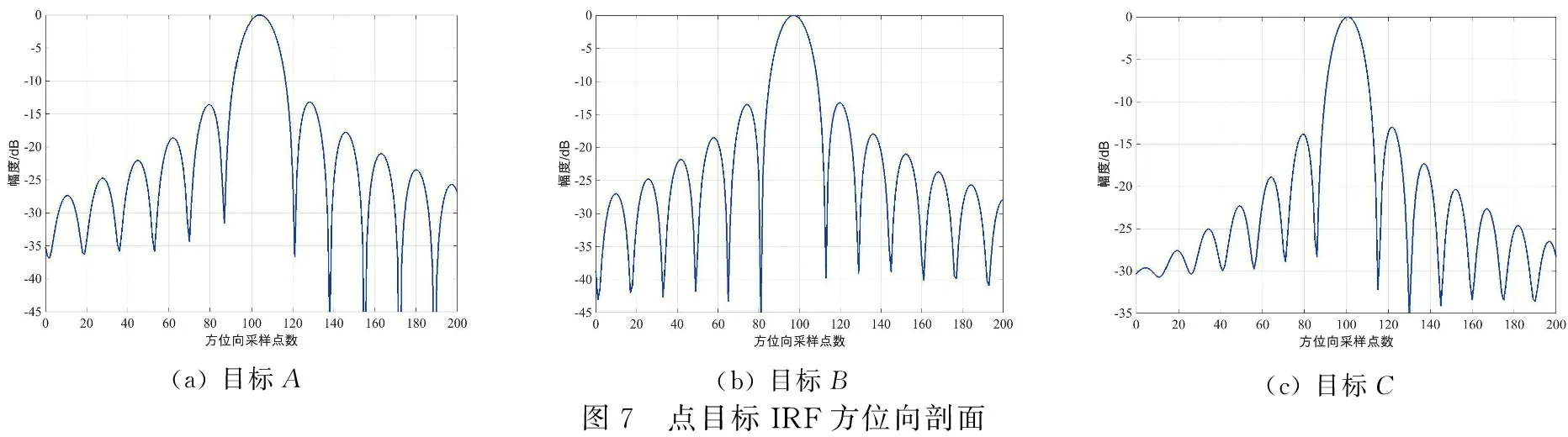
(a) 目标A (b) 目标B(c) 目标C图7 点目标IRF方位向剖面

(a) 目标A (b) 目标B(c) 目标C图8 点目标IRF等高线图

表2 点目标聚焦性能参数

除此之外，为了验证本文所提方法对斜视角度(0°～65°)的适应性，以凝视聚束模式为例，我们采用不同斜视角度进行重复性成像仿真实验。图9给出了点目标PA经处理后的PSLR和ISLR随斜视角度的变化曲线。图中表明在一定的斜视角度范围内，所提算法能够保证成像处理的有效性。综上所述，本文所提多模式统一化处理算法能够对斜视凝视和滑动聚束模式仿真回波进行频谱恢复与精确聚焦。

3.2 实测数据处理

本节利用所提算法对凝视和滑动聚束模式的实测数据进行处理，并与文献[17]所提方法及基于视线插值的极坐标格式算法(Polar Format Algorithm,PFA)进行对比。表3给出了实测数据主要参数。图10和图11 分别是X波段滑动与凝视聚束模式ROI的成像结果。图10(b)和图11(b)是局部场景对应的放大结果，图中地面建筑物轮廓分明，无明显的方位向散焦现象。

图9 斜视成像聚焦性能变化曲线

(a) 实测场景

(b) 对应的局部放大图图10 正侧视滑动聚束模式成像结果

(a) 实测场景

(b) 对应的局部放大图图11 本文方法对斜视凝视聚束模式成像结果

表3 实测数据主要参数

图12为文献[17]所提方法及视线插值PFA对斜视凝视聚束模式数据的处理结果，与图11对比可知，其成像质量较差，且几何失真现象较为严重。由实测数据成像结果可知，凝视与滑动聚束模式的数据经由本文所提算法处理，聚焦质量良好。因此，本文所提算法能够实现机载SAR多模式大斜视数据的统一化成像处理。

(a) 文献[17]所提方法

(b) 视线插值极坐标格式算法图12 两种对比方法对斜视凝视聚束模式成像结果

4 结束语

针对超高分辨斜视凝视与滑动聚束模式信号频谱混叠、距离方位耦合严重以及传统RMA难以结合距离空变运动补偿的问题，本文提出了一种基于ETSA和ERMA相结合的多模式统一化成像算法。(1) 基于方位Deramp的扩展型TSA方法重建混叠频谱，算法复杂度较低且不存在拼接误差。(2) LRWC实现斜视信号距离方位耦合的削弱，并且降低重建信号数据量以满足算法高效工程化需求。(3) 扩展型RMA能够结合azimuth scaling等算法进行运动补偿，实现多模式数据处理时的统一性和灵活性。(4) 点目标仿真及多模式斜视实测数据处理结果验证了所提算法的有效性。