一种基于异地处理的抵近探测雷达系统
2021-01-13马红星
马红星
(海装上海局驻合肥地区军事代表室,安徽合肥 230088)
0 引言
由于地球曲率的影响,为探测低空突防目标,需要同时实现雷达架高和雷达功率孔径的增加。现有的提升低空目标预警时间的主要手段有利用更大的载机平台,加装更大功率孔径积的雷达系统来提升远距离的预警能力。但大型的预警平台同样也面临滞空时间和战场生存的挑战[1-3]。此外,大型系统平台的复杂性以几何级数增加,并带来体积、重量、散热、维修、使用和保障等多方面的诸多问题。而且,通过增加雷达功率或孔径来提升雷达的探测威力往往也是事倍功半。根据雷达方程,为使雷达威力提升为原来的2倍,需要增加雷达功率孔径积至原来的16倍[4]。因而,探究一种可在有限功率孔径积下实现更远距离目标预警的新体制雷达,这对于预警体系的构建具有重要意义。
文章提出了一种增加转发站来实现定向远距离目标探测的新体制雷达。该雷达由发射站、转发站和接收站三部分组成。雷达工作时,发射站采用MIMO雷达[5-7]的工作方式,发射正交波形信号;转发站采用抵近目标的方式,进行目标回波信号的探测,以获取满足一定信噪比要求的信号,为避免与目标回波信号的相互干扰,转发站对接收到的信号进行错频回传;接收站接收回传信号,完成等效发射波束形成并进行信号处理,实现目标探测。该雷达的发射波束为正交波形,因而利用单通道接收的回波信号即可实现等效发射波束形成。转发站采用单个通道对目标回波进行接收时,仅需要对回波信号进行放大和错频回传,避免了接收过程中由于转发站接收天线指向和多通道信号回传过程中的相互干扰问题。这使得转发站功能简单,仅需要对接收到的信号进行错频回传,其在工作过程中可以不受探测信号的波形、带宽等参数的影响,损失或被截获后安全风险较小。同时,简单的功能结构也使得转发站具有常规雷达设备难以获取的小体积和低功耗等特点,为其灵活部署实现抵近探测创造了必要的基础条件。该雷达实现了在不改变发射站功率孔径积的前提下,通过将转发站抵近目标的方式,实现远距离目标的探测,为提升雷达远距离预警能力提供了一种可供参考的思路。
1 基本原理
该体制雷达由发射站、转发站和接收站三部分组成,原理示意图如图1所示。发射站发射正交探测波形信号;信号在空间中进行辐射,经目标散射后的回波信号被转发站接收,转发站对接收到的回波信号进行错频回传,接收站接收回传信号,进行等效发射波束形成并完成回传信号的处理,实现目标探测。
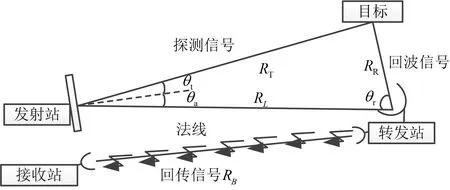
图1 雷达原理示意图
1.1 信号模型
考虑发射阵面是一个M个阵元组成的线阵,阵元间距为d,如图2所示。假定相邻阵元之间的频率间隔为Δf,第m个阵元发射信号的频率为fm,有
fm=f0+am·Δf
(1)
式中,am∈{0,1,2,…,M-1}为发射阵元的序号,f0为雷达工作频率。则第m个阵元的发射信号可以表示为
sm(t)=Re{xm(t)exp(j2πfmt)}
(2)
式中,xm(t)为第m个发射信号的复包络。第m个阵元的发射信号到达空间中某点的信号可以表示为
sm(t-τm)=Re{xm(t-τm)·
exp(j2πfm(t-τm))}
(3)
式中,τm为第m个发射阵元到该点的传播时延。
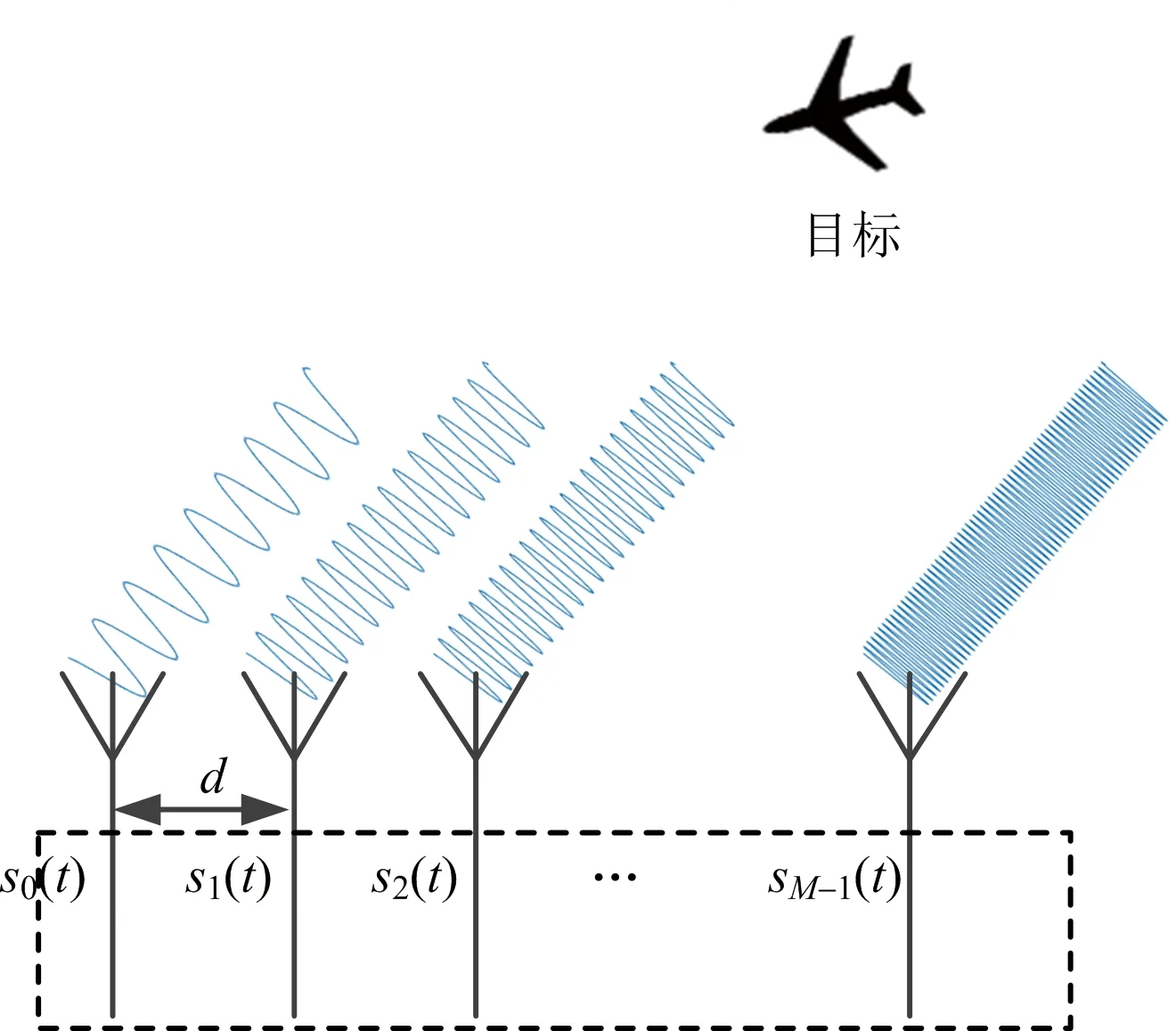
图2 发射站原理示意图
假定在p点有一个目标,其角度位置矢量为Θ,运动速度为v,则转发站接收阵元接收到的信号可表示为
rr(t,Θp,vp)=
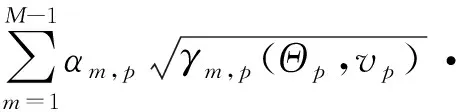
xm[γm,p(Θp,vp)(t-τm,p)]·
exp(j2π(f0+am·Δf)·
γm,p(Θp,vp)(t-τm,p))+n1(t)
(4)
式中,n1(t)为转发站接收到的环境噪声,τm,p为发射站第m个阵元经目标后到达转发站接收天线的时延,αm,p为发射站第m个发射阵元经目标p散射后到转发站接收阵元的衰减因子,γm,p(Θp,vp)为目标运动产生的拉伸因子,且
γm,p(Θp,vp)=1+fm,p(Θp,vp)/f0
(5)
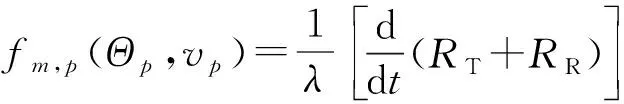
由于发射站发射的探测信号采用了正交波形信号,目标回波信号中包含了目标相对于发射站的相对方位信息,通过单个接收通道获取的目标回波信号即可实现等效发射波束形成。基于此,转发站基于单个接收通道获取目标回波信号,并将接收到的信号进行错频回传。错频传输的目的主要是为了防止探测信号和回传信号相互之间的干扰。转发站的工作原理如图3所示,转发站接收天线接收目标回波信号后经限幅低噪放,进行混频、滤波放大处理后经回传天线传输至接收站。
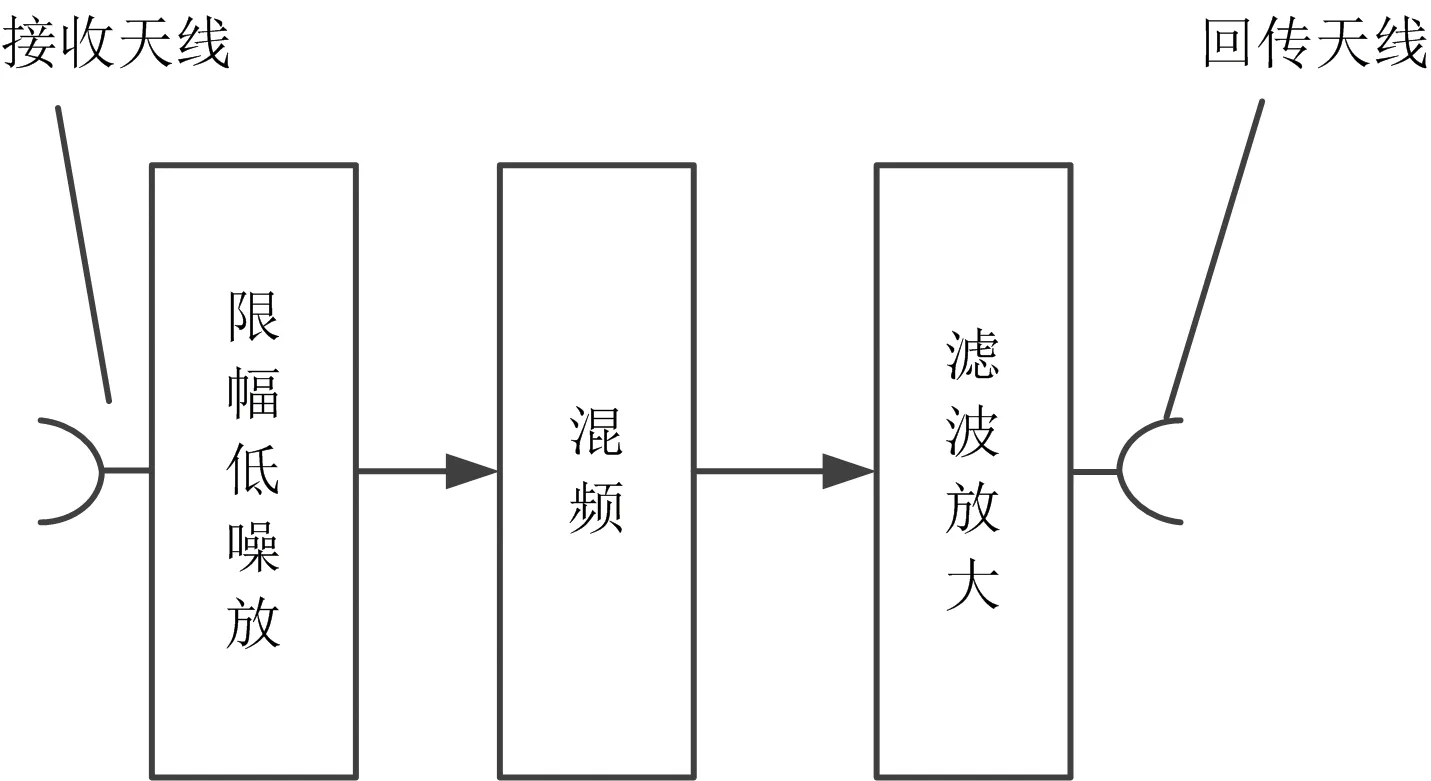
图3 雷达转发站工作原理图
不考虑雷达转发站内部对信号传输的影响,转发站对信号的影响仅为放大和频率调制。其输出端的表达式可以表示为
rr′(t,Θp,vp)=A·rr(t,Θp,vp)·
exp(j2π(f1-f0)t)
(6)
式中,A为信号增强倍数,fB为回传链路的工作频率。接收站接收到的信号为
r(t,Θp,vp)=
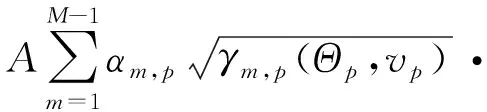
xm[γm,p(Θp,vp)(γB(ΘB,vB)(t-τB)-τm,p,d)]·
exp(j2π(f0+am·Δf)·
γm,p(Θp,vp)(γB(ΘB,vB)(t-τB)-τm,p,d))·
exp(j2π(f1-f0)γB(ΘB,vB)(t-τB))+
An1(t)+n2(t)
(7)
式中,τB为转发站到接收站的传播时延,γB(ΘB,vB)=1+fd/(fB-f0)为转发站和接收站相对运动产生的拉伸因子,fd为转发站和接收站相对移动产生的多普勒频移。
1.2 模糊函数
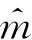
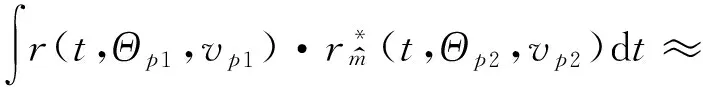
fmγm(γB1τB1+τm,p1,d))]·
(8)
其中,衰减因子为
相位函数为
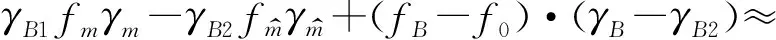
式中,Δfd1为目标相对于发射站和转发站的移动引起的多普勒频移,Δfd2为转发站与接收站的相对运动引起的多普勒频移。
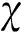
(9)
其中,exp[-j2π(fB-f0)(γB2τB2-γB1τB1)]为一个模为1的常数,导向矢量
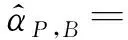
exp[j2π(fM-1+fd1)(τB+τM-1,p,d)]]T
(10)
协方差函数

exp(j2π(ΔamΔf+Δfd)t)dt
(11)
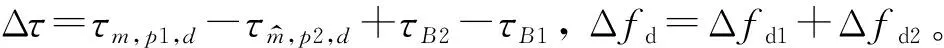
1.3 空间模型
从图1可知发射站、目标、转发站和接收站的空间关系。其中,发射站、转发站和接收站的位置可通过定位设备测定,相应地,可求得发射站与转发站之间的距离RL、转发站与接收站之间的距离RB、转发站与发射阵面法线的夹角θa。发射站、目标和转发站三者之间满足三角关系:
(12)
式中,RT为发射站到目标的距离,RR为转发站到目标的距离。此外,通过等效发射波束形成可以求解得到目标相对于发射站法线的夹角θt,信号处理可以计算得到信号从发射站经目标、转发站到接收站的总时延τall。
τall=(RT+RR+RB)/c+τp
(13)
式中,τp为信号在转发站内所经过的时间,即电磁波从转发站的接收天线到回传天线的传输时间,该值为固定值,可以通过时延测量方法测得并从总时延中减去。因而,根据三角关系,目标相对于发射站的距离为
(14)
式中,τw=τall-τp。
至此,求解得到了目标相对于发射站的角度θt和距离RT,实现目标的定位。
2 威力分析
雷达威力是雷达最为重要的指标之一,对该体制雷达的威力进行分析具有重要意义,其中雷达孔径和功率是设计过程中主要的变量。假定该雷达发射站的功率为P,发射增益为GT,目标的RCS为σ。雷达接收功率为
(15)
式中,Az为转发站接收阵面的有效孔径,AR为接收站接收阵面的有效孔径,Gzg为转发站的功率放大增益,Gzt为回传天线的增益。
不同于常规雷达,该体制雷达在转发站和接收站的接收过程中都会引入噪声,噪声功率密度可表示为
(16)
式中,Tsz为转发站接收端的噪声温度,Tsr为接收站接收端的噪声温度。对于宽度为τ的单个脉冲,当采用匹配滤波器时,接收站的接收机输出信噪比为
(17)
这里仅对比引入转发站后对于威力的影响,因此可忽略其他诸如积累脉冲、信号传输和处理等因素的影响。
常规雷达接收机的信噪比为
(18)
由于该体制雷达的变量较多,为了更为形象地对比该体制雷达与传统雷达的威力,基于真实应用场景对其进行了合理假设。
首先,雷达的孔径通常在几平方米到几十平方米之间,而转发站为了实现小型化其孔径通常要远小于发射站的孔径,不妨假定转发站的接收天线的孔径为原雷达的1/10,即Az=A/10。
其次,考虑到大型雷达的探测威力通常为数百乃至上千公里,而转发站抵近目标进行工作。假定RR=RT/20。
再次,雷达的噪声温度会随着接收机的不同而不同,但差异较小,因而假定Tsz=Tsr=Ts。
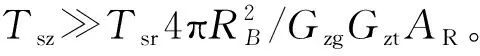
基于上述假设,求解可得RT=2.515R,即在该假设条件下,通过引入转发站可以将雷达的威力提升为原来的2.515倍。同时,通过更改转发站接收阵面的有效孔径或转发站与目标的距离,可以进一步优化雷达在特定方向上的探测威力。
3 仿真试验
为了进一步对该体制雷达系统的可行性进行探究,文章对其模糊函数开展了相应的数值仿真分析。假定雷达发射站的工作频率为3 GHz,发射阵面为16个阵元组成的线阵,阵元间距d=λ/2,回传链路工作频率为2 GHz。假定发射脉冲为脉冲宽度Te为10 μs的线性调频(LFM)信号波形[8-10],信号带宽B为0.4 MHz,不同阵元间信号的中心频点的频差Δf为0.4 MHz。
根据公式(12)可得,该体制雷达系统的模糊函数表达式不仅包含了探测链路的参数因子,同时也包含了回传链路的回传频率fB、时延τB和多普勒频移fd2等参数。即该雷达系统的模糊函数也受回传链路的影响。为了对雷达系统的模糊函数进行更为直观的分析,对参数变量进行了限制,假定转发站和接收站的位置相对固定。对雷达的模糊函数图进行绘制,如图4所示。
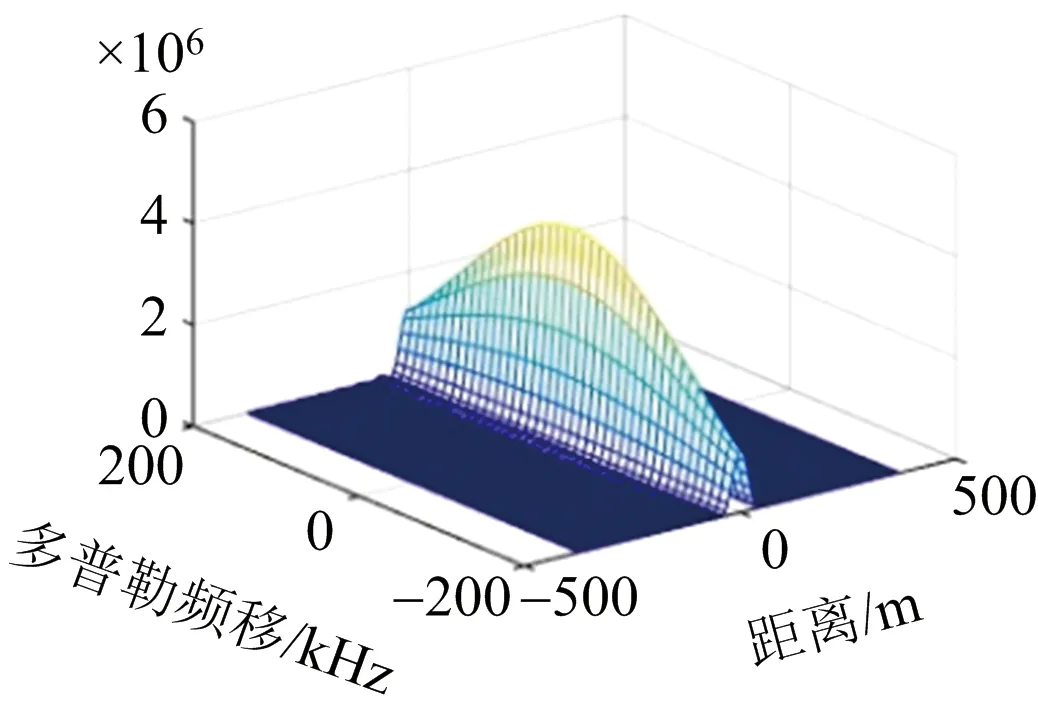
(a) 距离-多普勒模糊函数图
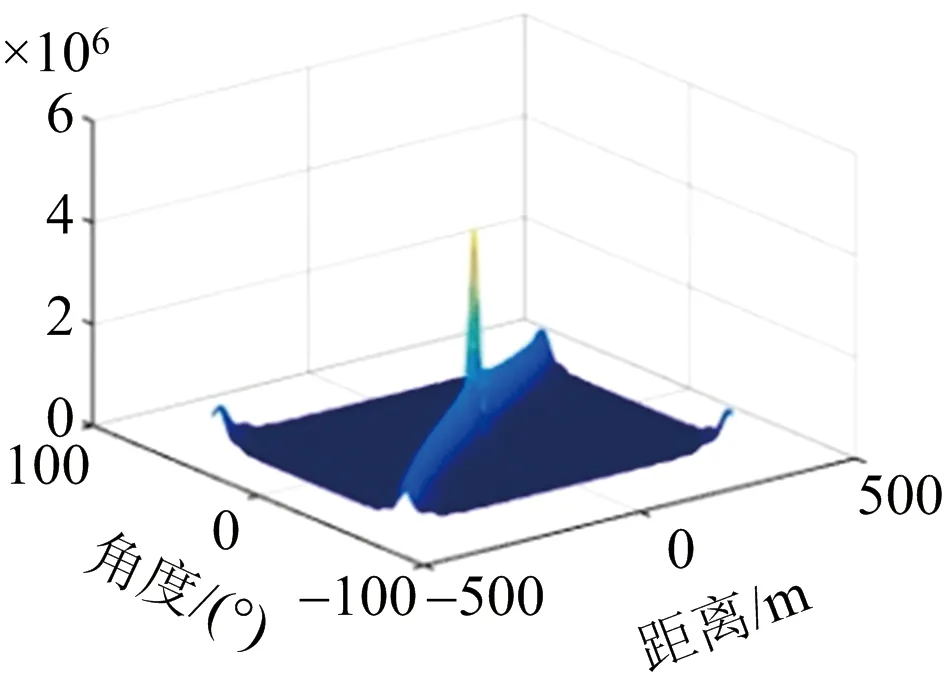
(b) 距离-角度模糊函数图
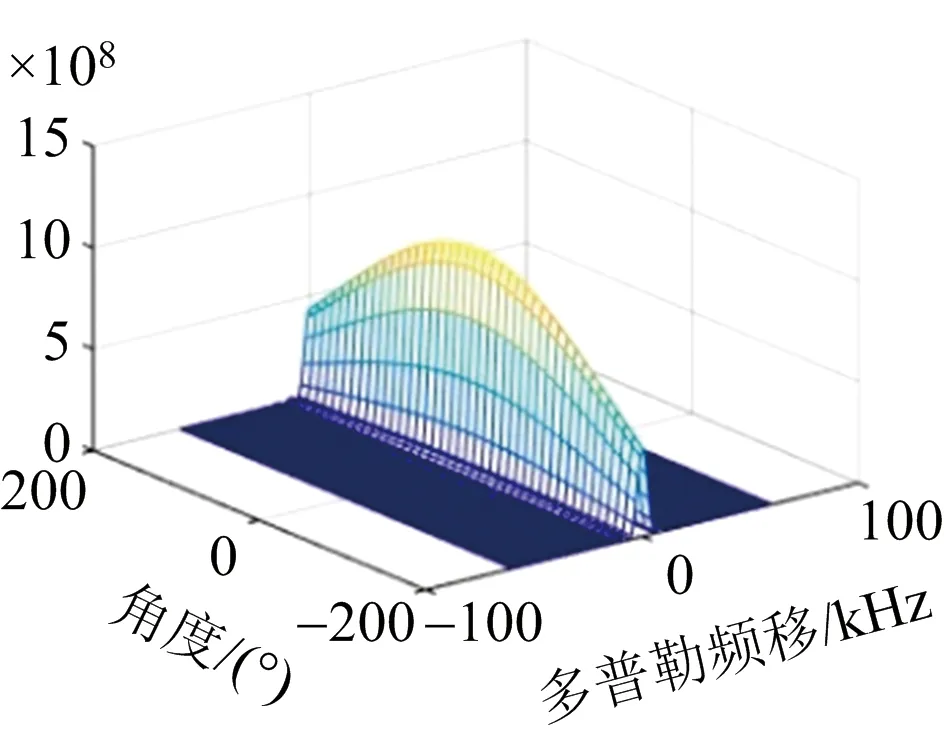
(c) 多普勒-角度模糊函数图图4 雷达系统的模糊函数图
图4(a)为距离-多普勒模糊函数图,该模糊图的形状为正椭圆形,距离速度之间的相互耦合较小,能够较好地实现对目标的分辨。图4(b)为距离-角度模糊函数图,该距离-角度模糊图呈现斜刀刃状,说明距离和角度两者之间存在较大的耦合度,其中一个的变化会影响到另一个的变化。图4(c)为角度-多普勒模糊函数图,其形状与距离-多普勒模糊函数图相似,也为正椭圆形,这说明目标角度和速度之间耦合性较小,具有较好的分辨率。
与典型的雷达系统不同,该体制雷达转发站接收回波信号后并不作计算处理,而是将接收到的回波信号进行错频回传,由接收站完成数据处理。在实际应用场景中,转发站通常根据需要会部署于无人机等移动平台上进行抵近探测。为考察回传链路对模糊函数的影响,文章对转发站和接收站之间存在相对移动时的场景开展了数值仿真。图5所示为转发站与接收站之间存在相对运动时的模糊函数图。实际场景中,转发站和接收站两者之间并不会存在如此之大的相对速度,这里只是为仿真两者之间的相对移动对于雷达系统模糊函数的影响。对比图5和图4中对应的模糊函数图可以看出,模糊函数图仅在多普勒维上发生了移动,其形状并没有发生明显变化。

(a) 距离-多普勒模糊函数图
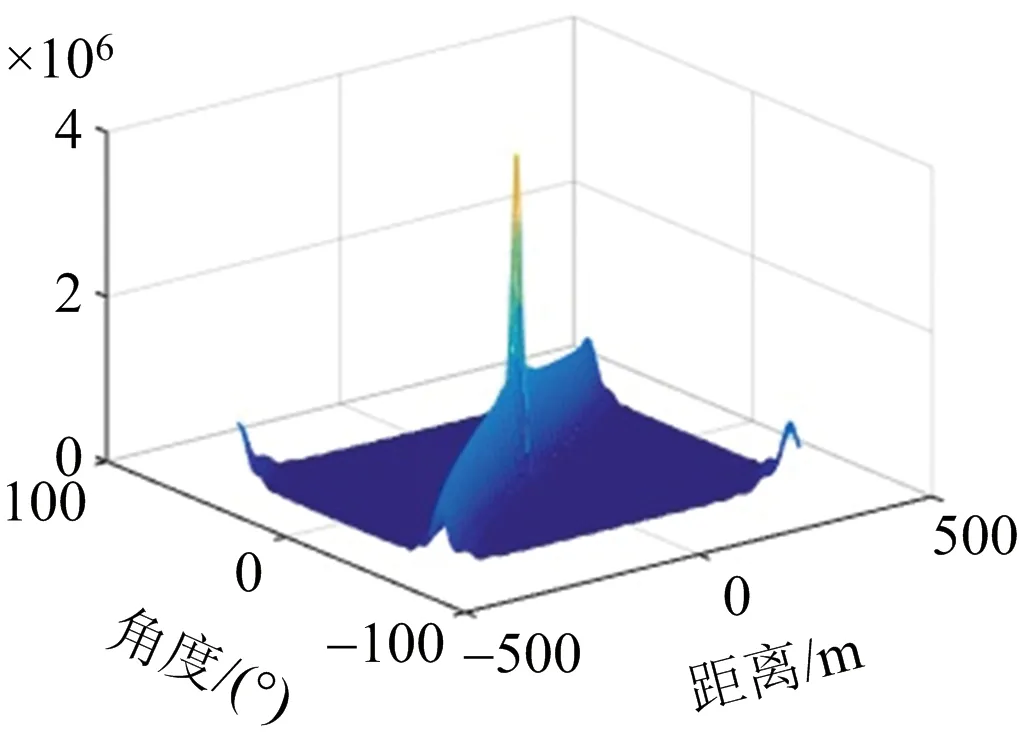
(b) 距离-角度模糊函数图
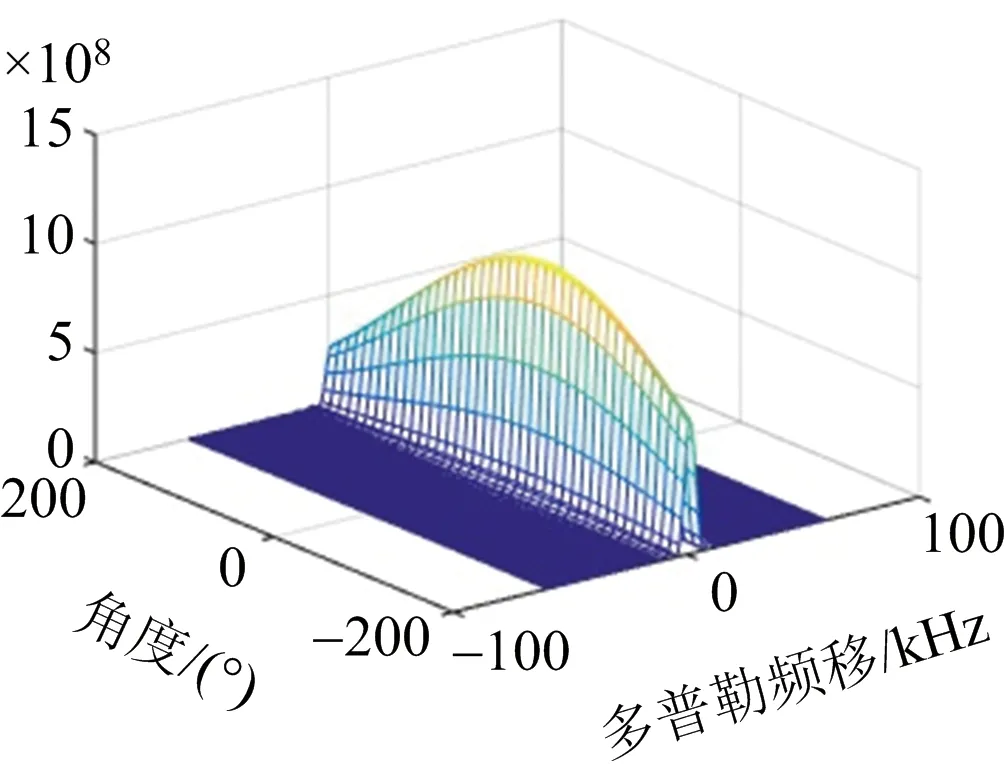
(c) 多普勒-角度模糊函数图图5 多普勒频移为10 kHz时雷达系统的模糊函数图
根据公式(14)可得,τB与τm,p,d的作用是相同的,在距离(时延)补偿后并不会对模糊函数造成影响,根据公式(15)可得,和的作用也是相同的,因此,当转发站与接收站两者之间存在相对移动产生的多普勒频移和目标相对于发射站(转发站)的相对移动产生的多普勒频移对模糊函数图的影响是相同的。
通过仿真得到的模糊图可知,该雷达系统能够实现对目标方位和距离的求解,证实了该雷达的可行性。
4 结束语
本文介绍了一种通过在探测链路中引入转发站,以实现远距离目标探测的新体制雷达。转发站采用了单个通道实现目标回波的接收并直接错频放大回传,功能简单,安全可靠。通过转发站抵近目标的方式,雷达系统获取更高的信噪比,实现在特定方向上的雷达威力的增强。通过转发站的合理部署,可以增强在特定海岛或海洋方向上的预警能力,对于提升基于本土构建的预警体系的预警能力具有一定的参考价值。
