T型尾翼飞机抖振试飞研究

2021-01-13高文涛张武林寇宝智

实验流体力学 2020年6期

高文涛,张武林,寇宝智

(中国飞行试验研究院飞机飞行试验技术研究所,西安 710089)

0 引言

抖振是边界层分离或湍流激起结构或部分结构的不规则振动。飞机发生抖振时，会产生一系列有害的后果，如飞机的操纵性和稳定性变差、飞行员驾驶疲劳进而降低其工作效率、结构易疲劳损伤进而影响飞行安全和使用寿命、机载设备的工作可靠性受到影响、旅客乘坐舒适性降低等。因此，美国[1]及中国[2]的运输类飞机适航标准均明确要求民用运输类飞机完成抖振试飞。

抖振按其成因大体可以分为两类:升力型抖振和非升力型抖振。升力型抖振一般指发生在机翼上的抖振,包括通常所说的大迎角抖振(大迎角飞行而引起的气流分离造成)和跨声速抖振(跨声速时由于激波-边界层干扰而引起的气流分离造成)。非升力型抖振一般指因飞行器外形突变产生的尾流激励而引起的翼面抖振,常见于飞机炸弹舱门或减速板打开、起落架放下、不合理的机身及座舱盖外形、雷达天线罩等引起的尾翼抖振[3]。

抖振研究主要有3种手段：风洞试验、数值模拟和飞行试验。飞机抖振为一种多学科综合性问题，主要涵盖了飞行品质、空气动力学、气动弹性、结构强度等多学科内容，仅依靠理论计算、数值模拟和风洞试验远不能满足研究的需要。飞行试验由于自身的特点，在抖振研究中发挥着举足轻重的作用[4]。

美国NASA 兰利研究中心[5]在国家跨声速实验室(NTF)对Boeing 767模型进行了风洞试验，研究了不同马赫数、不同迎角下飞机的抖振响应，建立了飞机的抖振边界。美国CFD研究中心的Sheta等[6]对F/A-18的垂尾抖振特点进行了数值计算，并与飞行试验数据进行了对比。洛克希德·马丁公司的Anderson等[7]通过对风洞试验和飞行试验的大迎角抖振数据进行分析，得出飞机在迎角大于26°时的抖振响应主要集中在垂尾的一阶弯曲模态。Sharma等[8]利用振动加速度传感器对P-3C飞机的大迎角抖振响应特点进行了飞行试验研究，得到了不同过载、空速、迎角组合情况的平尾上抖振响应的均方根分布情况。

国内对飞机的抖振研究多集中在数值计算和风洞试验方面，实际飞行中的抖振响应情况研究较少。李劲杰等[9-10]利用风洞试验与数值模拟等手段，对边条翼布局双垂尾抖振的发生机理及响应规律进行了研究。20世纪90年代国内曾进行过歼击机的抖振飞行试验研究[11]。2014年，李小路等[12]对某型歼击机的垂尾抖振飞行试验及抖振响应进行了研究。T型尾翼为高置平尾构形，在飞机以较大迎角飞行时，平尾处于机翼的分离尾流中，结构响应剧烈。但是国内对于T型尾翼飞机抖振响应的试飞研究较少，T型尾翼飞机的抖振响应规律及特点尚缺乏飞行试验研究。

为了研究T型尾翼飞机在飞行中的抖振响应特点及变化规律，为后续类似构形的飞机抖振试飞提供借鉴和经验，在飞机平尾及飞行员座椅地板处加装振动传感器，对抖振试飞方法、T型尾翼平尾及飞行员处抖振响应的特点及规律进行了研究。

1 试飞方法介绍

飞行试验中，抖振试飞主要有减速法、等坡度转弯法、收敛转弯法、平飞拉起法、俯冲拉起法、加速法等[13]。

在低速段主要采用减速法来获得飞机的抖振响应和抖振边界。由于低速段靠近飞机的左边界，飞机有进入失速区的风险，并且为了得到较好的抖振响应与飞机飞行状态的对应关系，一般要求每秒减速不超过1.852 km/h。

在中速段常用等坡度转弯、收敛转弯、平飞拉起、俯冲拉起等试飞方法。等坡度转弯和收敛转弯都是通过转弯的方式来增加过载。等坡度转弯可以获得过载和迎角参数与抖振响应的对应关系，但是较大坡度时飞机的状态难以保持。收敛转弯相当于连续进行等坡度转弯，可以节省试飞架次。但是相对于等坡度转弯，其马赫数和高度不好保持，迎角连续变化，因此很难建立抖振响应与迎角的对应关系，给数据处理带来较大困难。平飞拉起和俯冲拉起属于同一类动作，相对来说俯冲拉起较平飞拉起可以获得更大的过载。但是二者拉杆量均难以控制，并且飞机的姿态不好控制，保持过载和迎角的稳定比较困难，给数据处理增加了难度，并且也需要耗费较多的试飞架次。

在高速段通常用加速法。飞机以巡航构形在目标高度上配平飞机，然后进行1g加速飞行，直到发生抖振或达到设计俯冲速度改出。如果受发动机功率等限制使得飞机不能在平飞状态下发生抖振或达到设计俯冲速度，则应使飞机进入小角度的俯冲加速，直到出现抖振或达到设计俯冲速度改出。然而有的飞机在加速至右边界时未发生抖振，因此有时也在高速段使用收敛转弯法来获得高速段的抖振响应和抖振边界。但是，由于高速段靠近飞机的右边界，并且收敛转弯动作难以保持，会有较大的风险隐患，因此对试飞员的驾驶技术要求较高。

以上方法各有优缺点，需要根据实际情况选取不同的试飞方法。

2 试飞方法选取

飞机在某一高度、重量和速度组合下进行机动飞行时，飞机的受力满足以下等式[14]：

nW/δ=70 869.6CL·Ma2·S

(1)

其中：n为飞机过载，W为飞机重量(单位:N)，δ为压力比，CL为升力系数，Ma为马赫数，S为机翼参考面积(单位:m2)。

对于特定的飞机，机翼参考面积S是确定的，因此可以通过选择不同的nW/δ值得到CL与Ma的关系。

图1为等nW/δ曲线。图中C1、C2、C3曲线为等nW/δ曲线。沿着某一条等nW/δ曲线进行减速飞行时，如进行机翼水平失速(n=1，W、δ保持不变)、转弯失速(n>1，W、δ保持不变)等飞行动作，随着Ma减小，等nW/δ曲线与抖振边界相交，可以得到飞机在低速区的初始抖振点。同理，在高速区可以通过加速法得到飞机的初始抖振点。而在中速范围内可以通过增大nW/δ来得到飞机的初始抖振点。考虑到飞行试验的经济性，在给定高度、给定重量、给定Ma下可以通过增大过载n来得到中速范围的初始抖振点。结合上节介绍的不同试飞方法的优缺点，一般选用收敛转弯法(n增大，W、δ保持不变)来进行中速段的抖振试飞。波音公司的Boeing 767-200飞机即是选取收敛转弯法进行抖振试飞[15]。

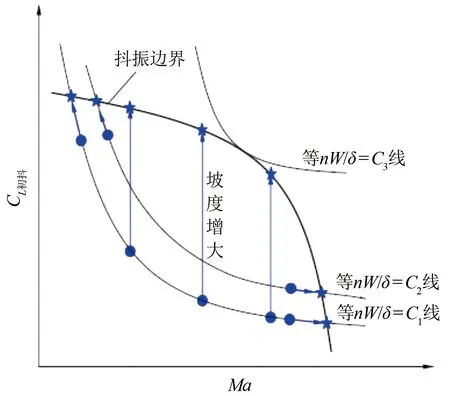
图1 CL初抖-Ma抖振边界与等nW/δ曲线Fig.1 CL buffet onset-Ma buffet boundary and lines of equal nW/δ

3 飞行试验

在飞机左、右平尾的中部和尖部的前后缘处加装了8个振动加速度传感器，测量平尾的法向振动加速度响应，如图2所示。在飞行员座椅地板处加装了振动加速度传感器，测量抖振发生时飞行员座椅处的垂向振动加速度响应。

图2 平尾上振动加速度传感器布置图Fig.2 Layout of vibration acceleration sensors on the horizontal tail

依据上节所述原则，规划出如下抖振试飞状态点(见图3)，在高高度、中高度、低高度3个高度剖面分别进行抖振试飞。从图1可知：在中低马赫数区，抖振边界比较平缓，故规划的试验点比较稀疏；在中高马赫数区，抖振边界变化率较大，故规划的试验点比较密集。

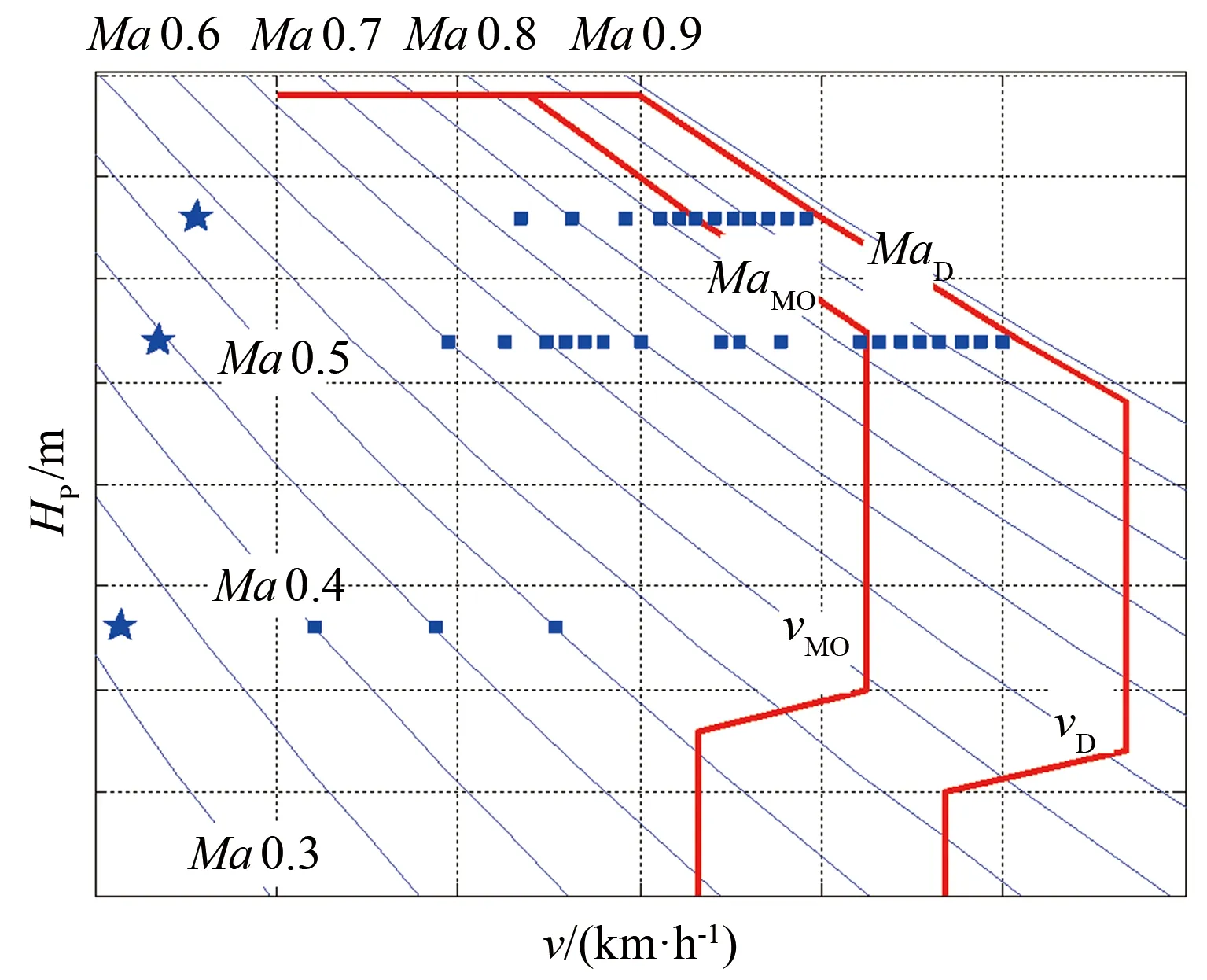
图3 某飞机抖振试飞状态点Fig.3 Buffet flight test points on an aircraft

图3中横轴为飞行速度v(单位:km/h)，纵轴为高度Hp(单位:m)，斜线为等马赫数曲线，vMO/MaMO为最大使用速度/最大使用马赫数，vD/MaD为设计俯冲速度/设计俯冲马赫数，正方形标志的状态点为收敛转弯试飞状态点，五角星标志的状态点为减速法试飞状态点。

图4给出了典型减速法的飞行曲线，图5给出了典型收敛转弯的飞行曲线。

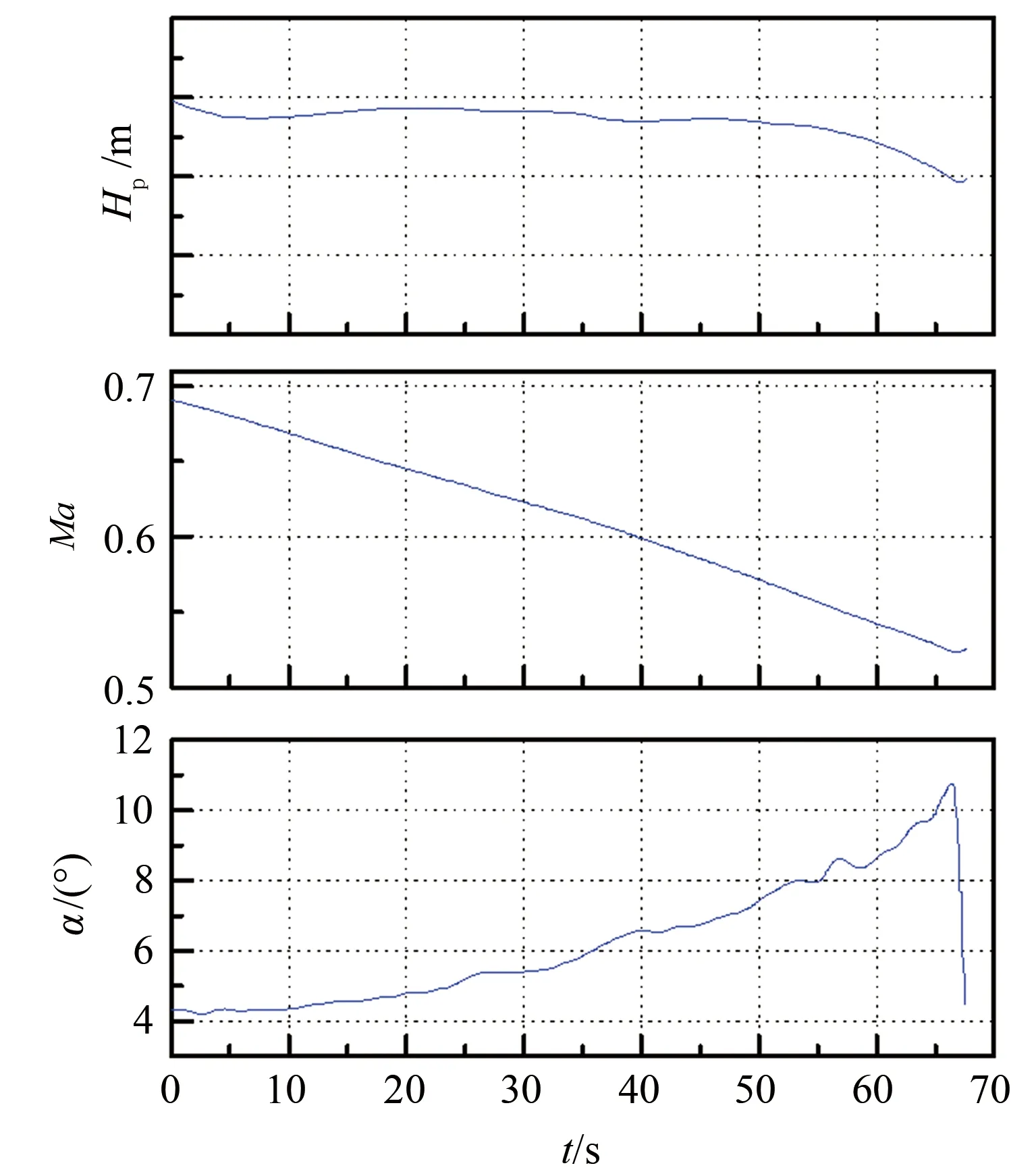
图4 典型减速法时间历程Fig.4 Typical time history curves of the velocity reduction method

由图4可知，减速法试飞过程中，高度近似不变(即可近似认为nW/δ不变)，随着Ma减小，在迎角α增大到11°左右时操纵飞机改出当前飞行状态，避免发生失速。由图5可知，收敛转弯过程中，高度近似不变，坡度φ逐渐增大即过载n逐渐增大(即可认为nW/δ逐渐增大)，在迎角增大到6°左右时操纵飞机改出当前飞行状态，避免发生失速。

图6和7分别给出了飞机在典型减速法和典型收敛转弯动作时的振动加速度a的响应曲线(g为重力加速度)。

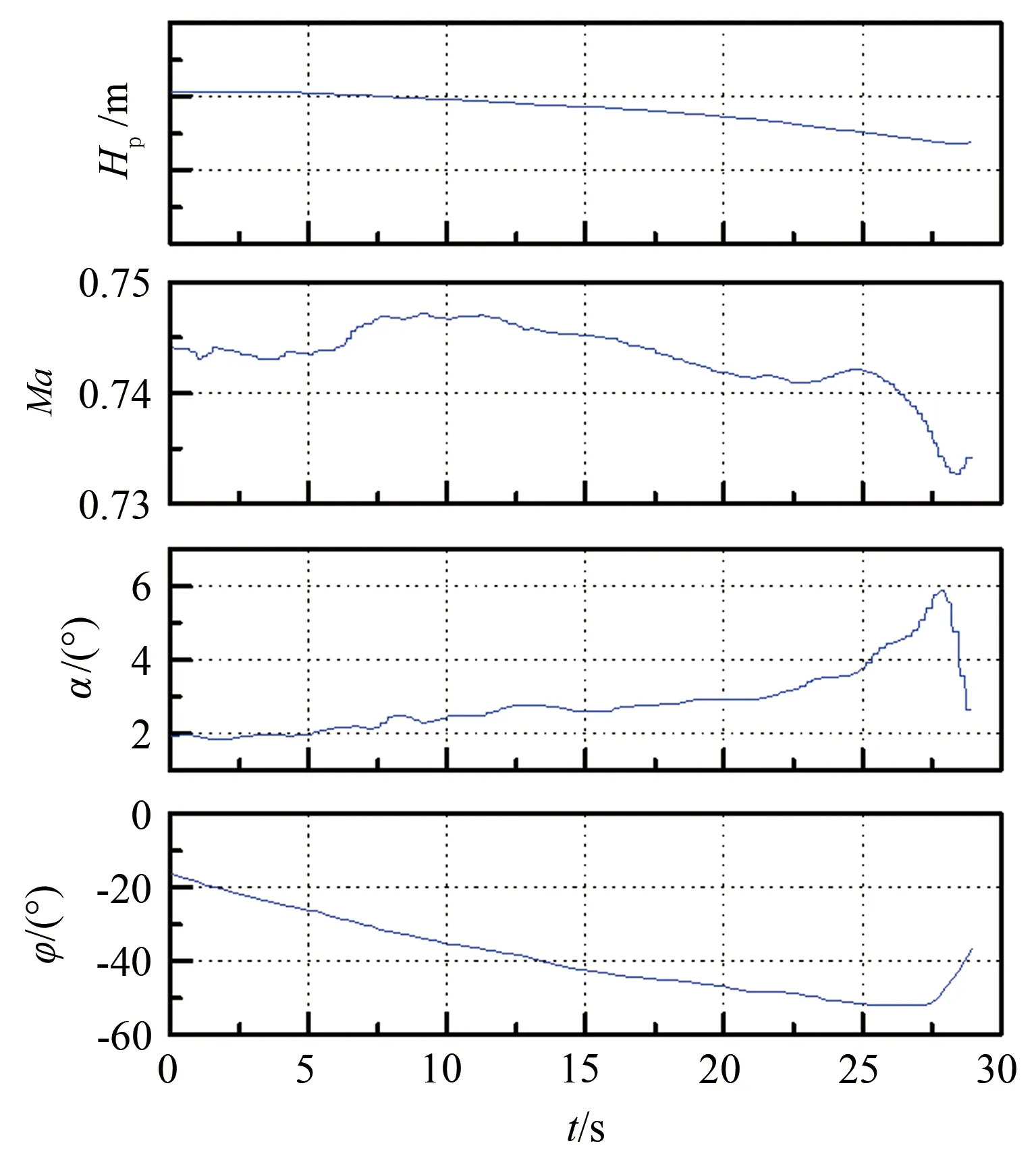
图5 典型收敛转弯时间历程Fig.5 Typical time history curves of the wind-up turn method

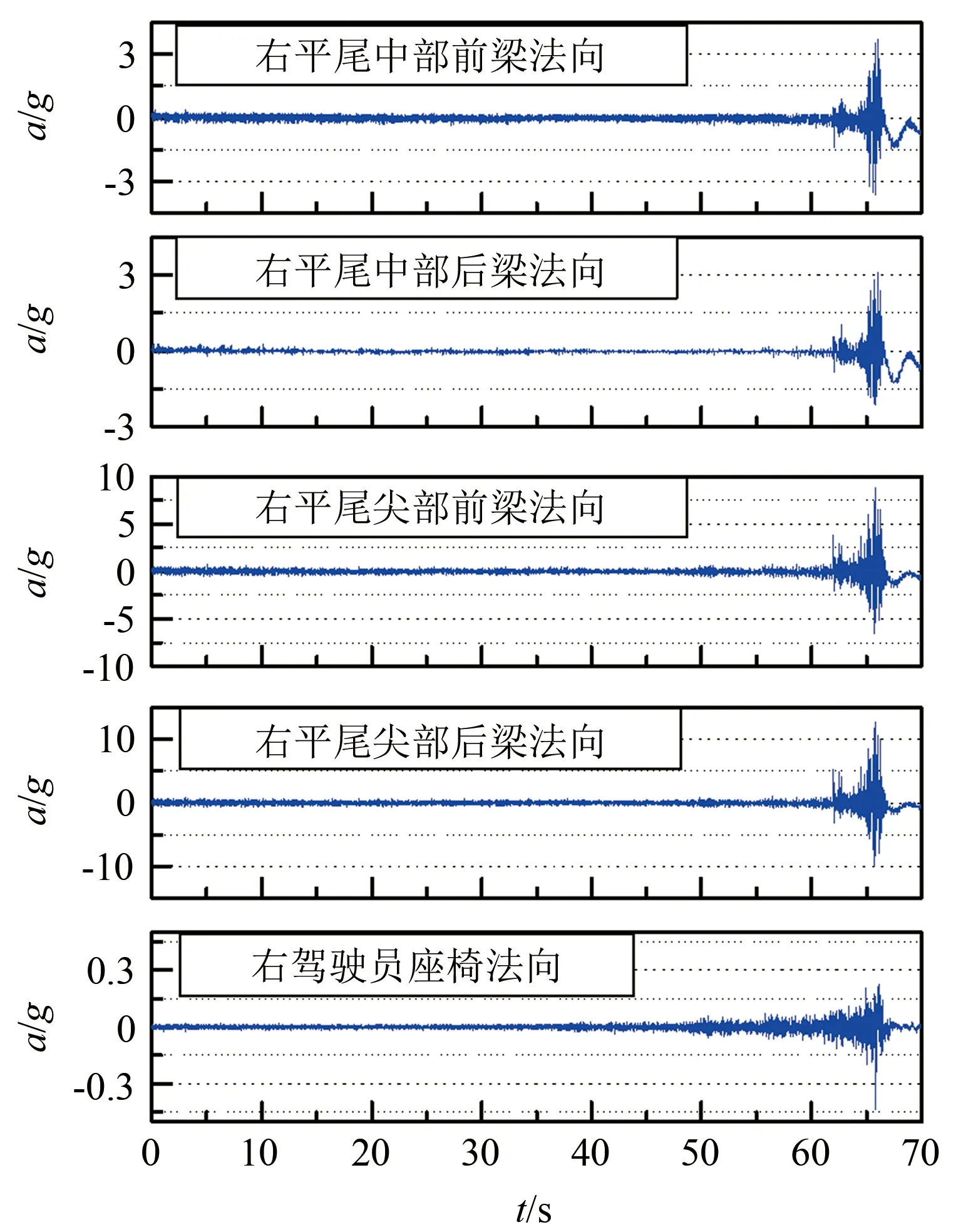
图6 典型减速法振动加速度时间历程Fig.6 Typical vibration acceleration time history curves of the velocity reduction method

可以看出：在迎角较小时，随着迎角增加，平尾各处及飞行员处的振动加速度响应无明显变化；在迎角增大到一定程度时，随着迎角增加，平尾各处及飞行员处的振动加速度响应明显增大。

以减速法飞行时平尾尖部后梁法向振动加速度响应为例，振动加速度响应时域最大值由0.9g左右增大到12.8g，增大了一个数量级。

图7 典型收敛转弯振动加速度时间历程Fig.7 Typical vibration acceleration time history curves of the wind-up turn method

4 飞行试验结果分析

4.1 平尾抖振响应时域分析

图8给出了在高高度剖面进行减速飞行时，平尾上各振动测点加速度的时域均方根随迎角的变化曲线。图9给出了在中高度剖面、以Ma0.74进行收敛转弯的过程中，平尾上各振动测点加速度的时域均方根随迎角的变化曲线。

可以看出：迎角较小时，抖振响应随迎角变化不明显；随着迎角的增大，平尾上各个测点的振动响应增大。平尾尖部的振动大于平尾中部的振动，平尾尖部后缘的振动大于平尾尖部前缘的振动。减速飞行过程中，左、右平尾相同部位的振动响应水平基本一致。在收敛转弯过程中，左、右平尾相同部位的振动响应水平不一致(左平尾尖部的振动大于右平尾尖部的振动)，可能是收敛转弯过程中带侧滑引起的。

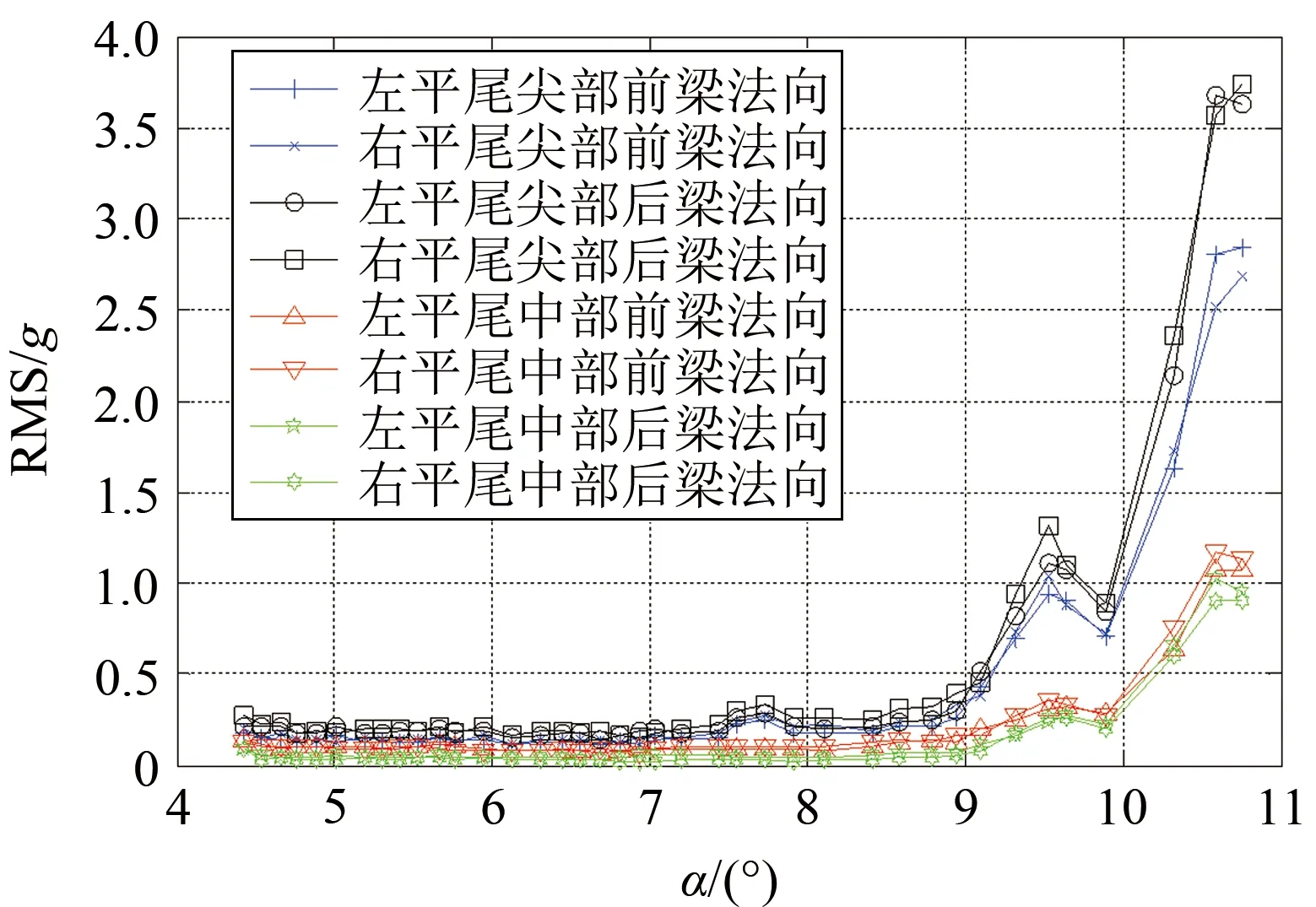
图8 高高度、减速法，平尾各振动测点时域均方根随迎角的变化曲线Fig.8 The vibration acceleration RMS curves with the angles of attack (High altitude,the velocity reduction method)

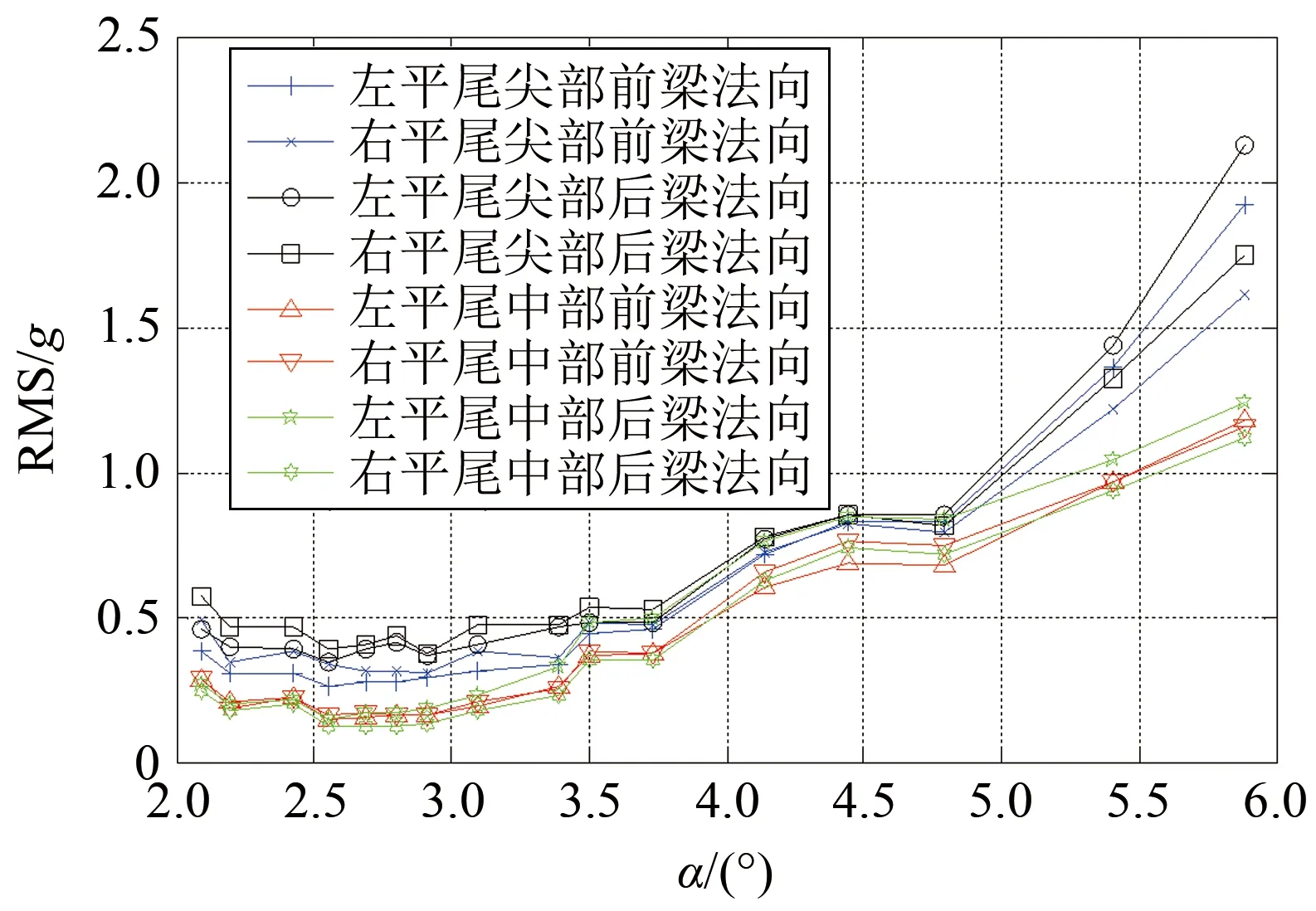
图9 中高度、Ma=0.74，收敛转弯，平尾各振动测点时域均方根随迎角的变化曲线Fig.9 The vibration acceleration RMS curves with the angles of attack (Mid-altitude,Ma=0.74,wind-up turn)

为了研究相同高度下抖振响应与迎角、马赫数的相互关系，对不同迎角水平、不同马赫数下的左平尾尖部后缘振动加速度均方根值进行分析，如图10所示。

图10分别给出了迎角为4.5°、5.5°、6.5°和7.5°时，左平尾尖部后缘振动加速度均方根值随马赫数的变化关系。可以看出：迎角一定时，抖振加速度响应的均方根值随马赫数的增大而增大；马赫数一定时，抖振加速度响应的均方根值随迎角的增大而增大。

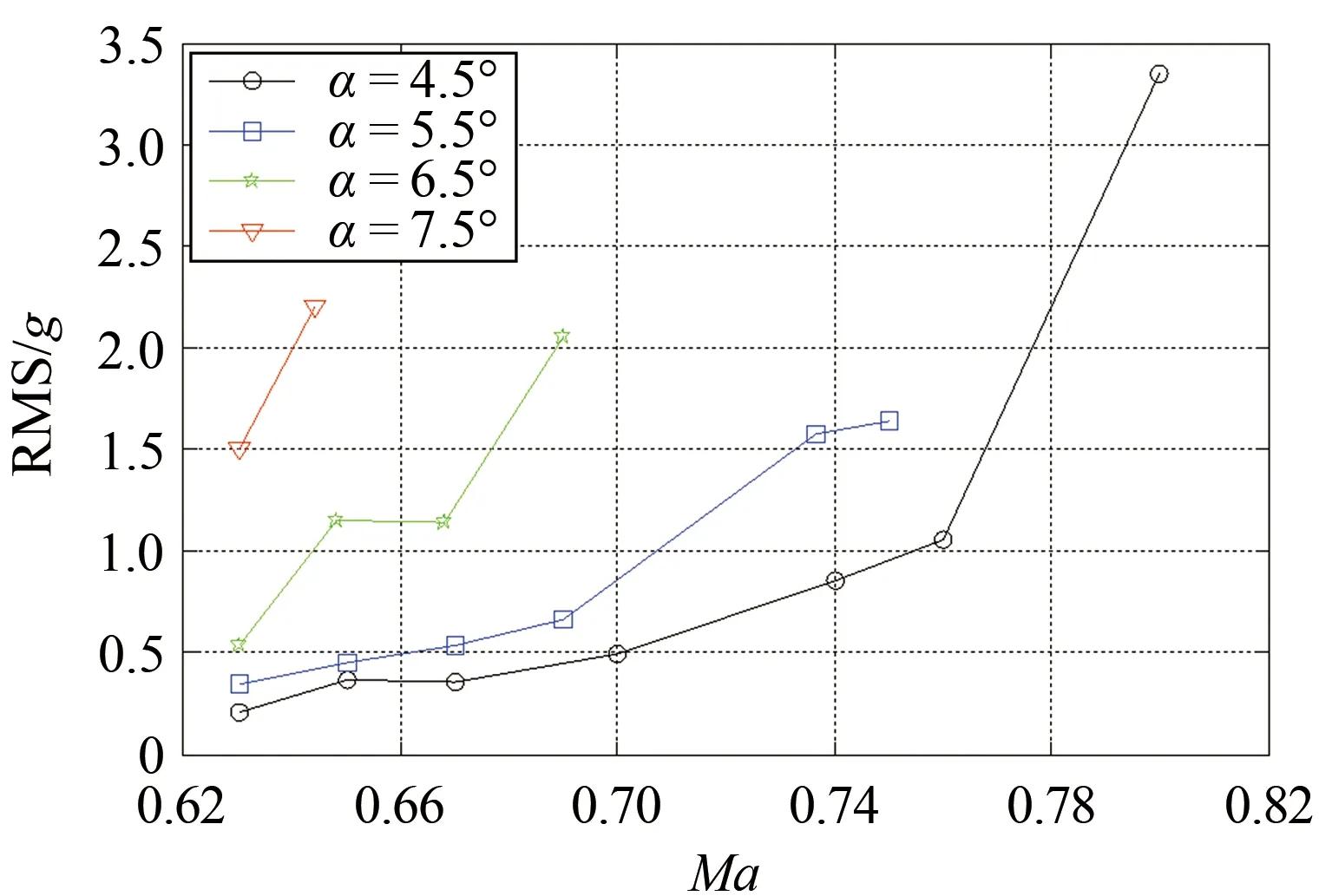
图10 中高度，左平尾尖部后缘振动加速度均方根值随马赫数变化曲线Fig.10 The vibration acceleration RMS curves with Ma of trailing edge of the left horizontal tail tip (Mid-altitude)

4.2 平尾抖振响应频域分析

为研究飞机抖振响应的频率分布，对减速法和收敛转弯过程中飞机平尾的抖振加速度响应做小波时频分析。图11和12分别为减速法和收敛转弯法时右平尾尖部后缘振动加速度小波时频图，颜色越亮表示振动量值越大。

可以看出：抖振发生时，各频点的振动量值均有所增加；抖振响应主要集中在5.5、9.4和21.0 Hz附近，对应的飞机模态分别为平尾对称一阶弯曲(5.26～6.02 Hz)、机翼对称二阶弯曲(9.26～10.59 Hz)、平尾反对称二阶弯曲(19.97～22.40 Hz)。

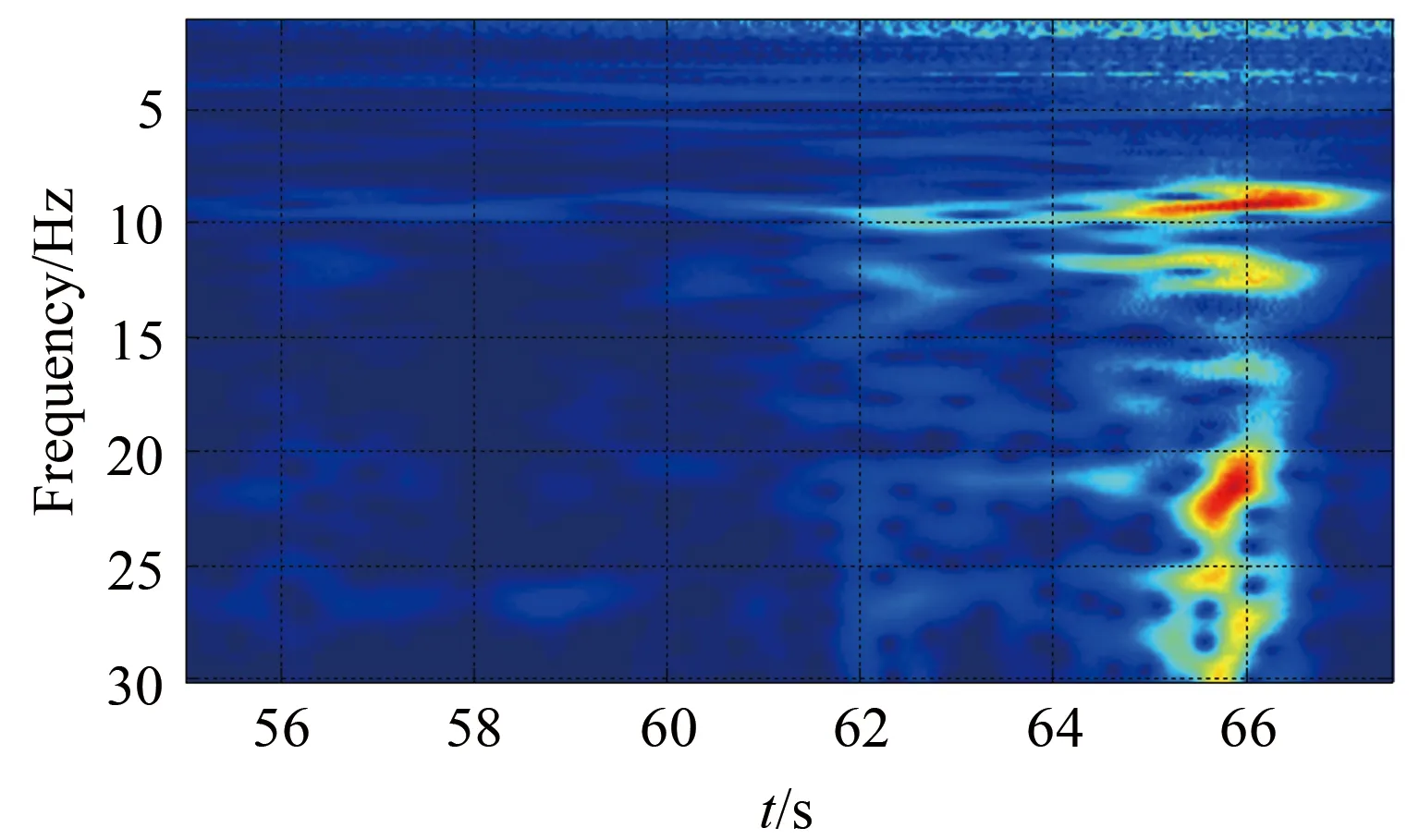
图11 高高度、减速法，右平尾尖部后缘振动加速度时频图Fig.11 Time-frequency figure of trailing edge of the right horizontal tail tip (High altitude,the velocity reduction method)

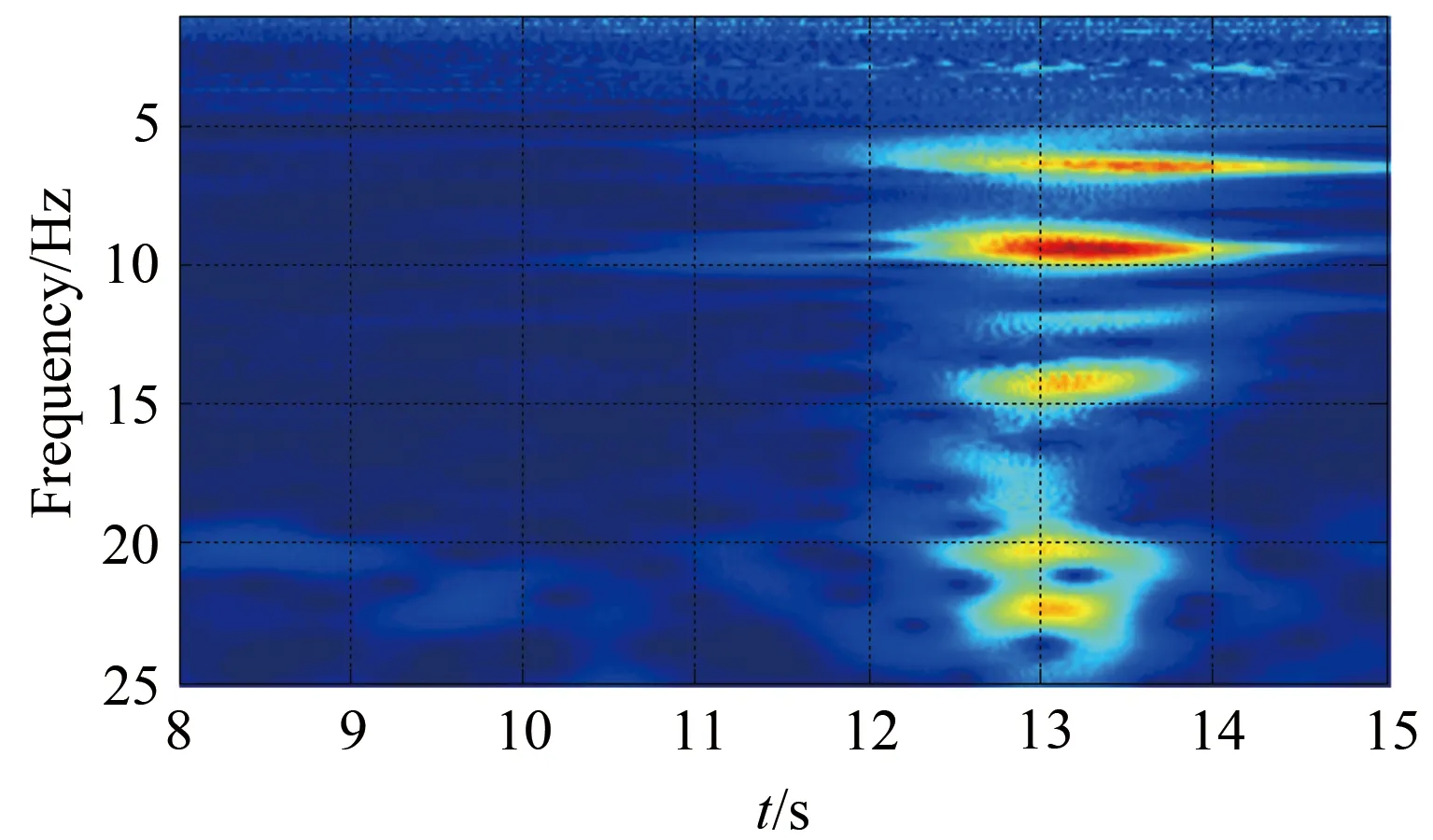
图12 中高度、Ma=0.63,收敛转弯，右平尾尖部后缘振动加速度时频图Fig.12 Time-frequency figure of trailing edge of the right horizontal tail tip (Mid-altitude,Ma=0.63,wind-up turn)

该型飞机的平尾没有9.4 Hz附近的模态，之所以出现9.4 Hz成分的振动响应，是因为机翼后缘的气流分离引起的交变载荷激起了机翼的对称二阶弯曲模态，导致分离流中叠加了较高能量的9.4 Hz附近的频率成分，从而激起了平尾的振动，属于强迫振动的范畴。在不同马赫数、迎角、过载的组合下，平尾抖振响应的主峰有所不同，但是峰值频率均为5.5、9.4和21.0 Hz左右。

在中高度以Ma0.63进行收敛转弯时,平尾抖振响应的主峰为9.4 Hz左右。图13给出了9.4 Hz的振动加速度值随时间的变化曲线。其中,横轴为时间(单位：s)，纵轴为9.4 Hz的振动加速度对g的无量纲值。

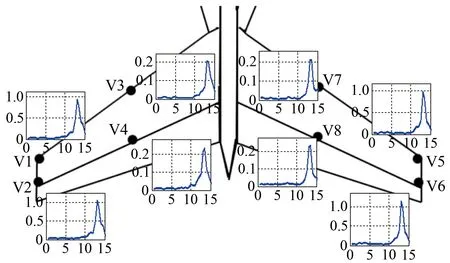
图13 中高度、Ma=0.63,收敛转弯，9.4 Hz振动加速度值时间历程曲线Fig.13 The vibration acceleration time history curves of 9.4 Hz (Mid-altitude,Ma=0.63,wind-up turn)

可以看出：抖振发生时，平尾上同一肋截面上后缘的9.4 Hz抖振响应大于前缘，尖部的9.4 Hz抖振响应大于中部，这与时域分析的结果是一致的。随着时间的推移，即随着迎角增大，平尾的抖振响应也逐渐增大。

4.3 飞行员处抖振响应分析

由国军标966-90[16]可知：在脚或臀部至头方向(z向)上，人体对中心频率为4～8 Hz的三分之一倍频程频率范围的振动最敏感，耐受度最低。而该型飞机飞行员位置处的抖振响应峰值频率正好在4～8 Hz范围内，因此抖振会对飞行员的工效性及舒适性有明显影响。图14为发生抖振时飞行员座椅处垂向振动响应的三分之一倍频程归纳谱。

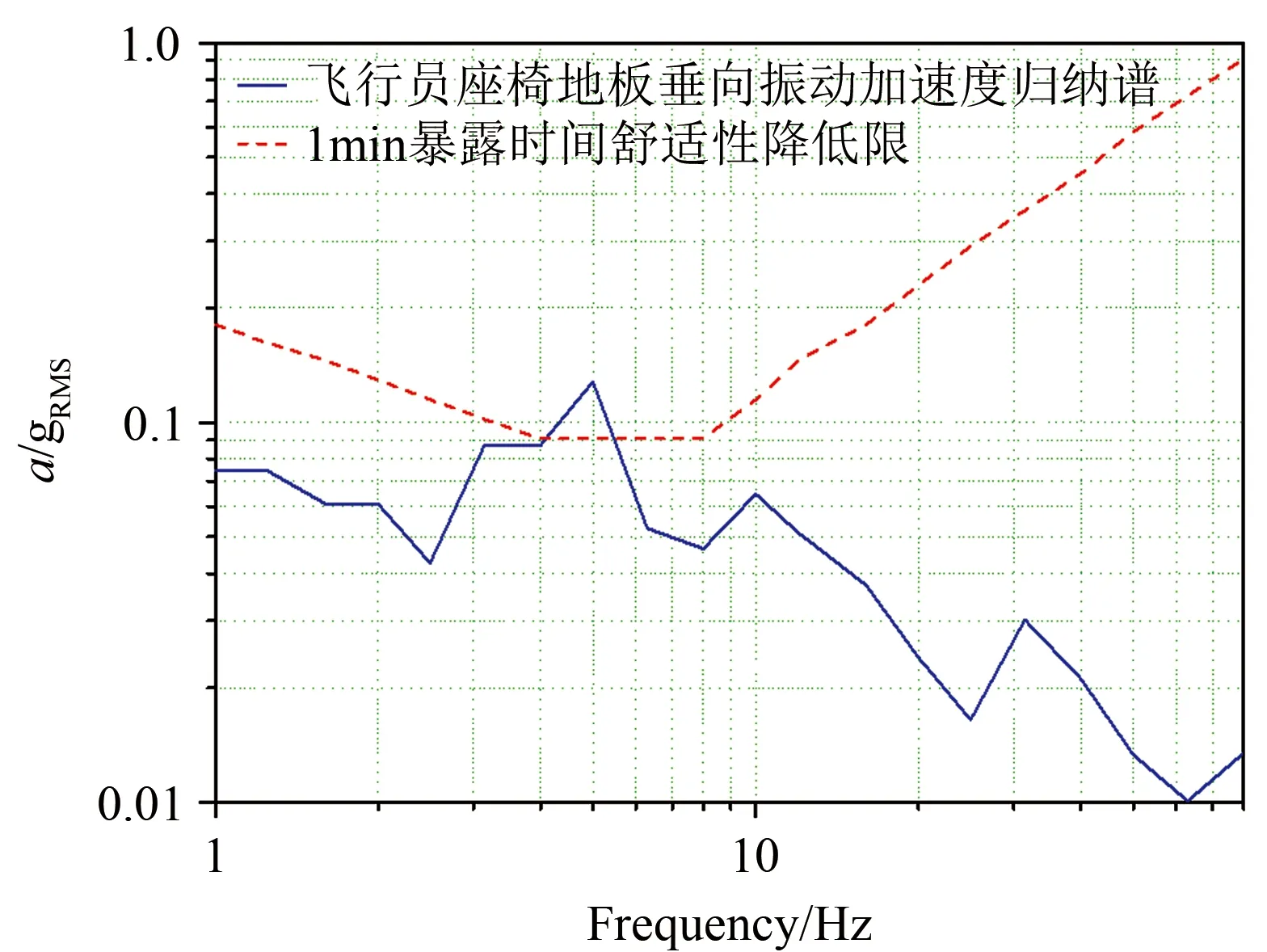
图14 飞行员座椅处垂向振动归纳谱Fig.14 Inductive spectrum of the vertical vibration at the pilot’s seat

图中,实线为飞行员座椅地板处垂向振动加速度归纳谱，虚线为国军标966-90规定的1 min暴露时间舒适性降低限。可以看出：飞行员座椅地板处垂向抖振响应频率主峰为5 Hz左右(对应平尾对称一阶弯曲模态)，中心频率为5 Hz的抖振响应归纳谱值为0.128g,相关国军标规定的1 min暴露时间5 Hz的舒适性降低限为0.091g,即在5 Hz中心频率处飞行员座椅地板的抖振响应超出了1 min舒适性降低限，也就是说抖振会影响人员的舒适性。

平尾抖振响应的频率成分主要为5.5、9.4和21.0 Hz左右，而飞行员座椅处垂向抖振响应的频率成分主要为5 Hz左右，即两处结构的抖振响应的频率组成不同。

目前,试飞中确定抖振边界的方法是结合飞行员主观判断与飞行员座椅地板处垂向振动加速度量值。AC25-7D咨询通告[17]和适航标准研究报告[18]推荐该量值为±0.05g，ERJ190-100飞机[19]使用的是±0.08g，该量值因机型不同而不同。抖振实质是飞机翼面结构的振动响应，通过飞行员座椅处的振动来判断是否发生抖振是一种间接方法。前文分析了飞行员座椅地板处的振动和飞机翼面结构的振动响应的频率组成不同，故飞行员座椅地板处的抖振响应不能全面反映飞机翼面结构的抖振响应。因此，应综合考虑飞机翼面结构和飞行员处的振动响应来确定抖振边界。