地铁车站屏蔽门风压特性试验研究
2021-01-13曾令伟易富民王汉封黎良桥
曾令伟,易富民,王汉封,*,黎良桥
(1.中南大学 土木工程学院,长沙 410075;2.成都轨道交通集团有限公司,成都 610041)
0 引 言
地铁站台的屏蔽门(Platform Screen Door,PSD)是地铁系统的重要组成部分之一。它将站台与列车运行区域分开,维持站内环境,确保乘客安全[1-4]。通常,屏蔽门设计需要考虑人员荷载、风压荷载、冲击荷载以及地震荷载等影响[5],这些荷载均是从静力或等效静力角度考虑屏蔽门所受的侧向荷载,即垂直于屏蔽门的荷载。随着地铁列车运营速度的提高及发车频次的增大,列车在隧道中行驶时产生的风压荷载不仅会影响屏蔽门结构安全,还可能影响其正常开闭,进而影响整个地铁线路的正常运营[6]。但在中国现行的《地铁设计规范》[7]中,尚未涉及屏蔽门开闭过程中所受的侧向荷载值。
已有大量文献对隧道内的空气动力学问题进行了研究[8-17]。当列车进入隧道时,由于空间突然受限,车头前方产生压缩波并在隧道中以声速传播[17-19]。当压缩波到达隧道出口时,会以微压波形式向外释放[20];同时,在出口形成的膨胀波反射回隧道内。值得注意的是,当列车经过隧道中的区间泄压井时,由于泄压井壁面限制了空气的横向流动,空气受到压缩而压力升高,也会在隧道中产生压缩波[21-23]。
为研究列车过站对屏蔽门风压响应的影响,Chun等[10]采用数值模拟方法研究了列车以不同速度过站时的屏蔽门风压,讨论了站内泄压井开闭状态对屏蔽门风压的影响。Kim[13]通过现场实测研究了列车以不同速度过站、站内会车等工况下的全封闭屏蔽门风压荷载,发现列车交会将显著增大屏蔽门风压,且各测点风压极大值均出现于车头经过该测点时,列车经过后风压迅速变为负值;值得注意的是,在列车距离站台尚有500 m左右时,屏蔽门风压即开始逐渐增大。Zhou等[14]通过1∶20的模型弹射试验研究了单车过站、会车对车身表面及屏蔽门风压的影响,结果表明,屏蔽门风压受压力波与列车风的共同影响,其极值沿行车方向逐渐减小。Luo等[15]采用数值模拟方法分析了高速列车过站时的屏蔽门瞬时压力特性,发现列车过站过程中屏蔽门所受的正压极值远大于负压极值。
列车过站时的屏蔽门风压极值与行车速度、阻塞度、车头形状、泄压井以及列车与屏蔽门的间隙等因素相关。相关研究表明:屏蔽门风压与车速大致呈二次方关系[10,24-26];屏蔽门风压极值随阻塞度增大而增大,两者近似为线性关系[23,25];车头形状会影响风压变化趋势,但对风压极值影响很小[24,27];站台两端设置泄压井可显著降低屏蔽门风压极值,最大降幅可达30%左右[22,25,28];列车与屏蔽门的间隙由130 mm增加至425 mm后,列车过站时的屏蔽门风压极值可降低约53%[26]。
列车过站时的屏蔽门风压极值对屏蔽门的强度设计提出了要求;但此时屏蔽门不需开闭。通常,只有当列车停靠站台时才需开闭屏蔽门,此时车速为零,无列车风效应。在列车停靠站台时,曾发生屏蔽门无法正常开闭的情况,对其原因目前尚无统一认识。本文采用弹射试验的方法,研究列车车速与泄压井对隧道内压力的影响规律,并以此为基础对比研究屏蔽门风压变化规律。采用轻质泡沫模型模拟站内停靠车辆,研究后方来车对屏蔽门风压的影响规律(本文称为“跟随工况”,Tracing case),分析高频次发车条件下屏蔽门无法正常开闭的原因。
1 试验模型及装置
1.1 试验装置
本文弹射试验在中南大学轨道交通安全教育部重点实验室的动模型弹射系统上进行。该系统总长164 m(加速部分57 m、试验部分50 m、制动部分57 m),最高弹射速度500 km/h[14,26]。弹射试验开始时,列车模型与弹射试验装置相连接,列车在弹射装置上获得一个初始速度并匀速驶向客站。详情请参考文献[14,26]。
1.2 试验模型与测点布置
全隧道模型、列车模型和站台模型如图1所示,模型缩尺比为1∶20。图1(a)为全隧道模型,作为隧道-站台模型(列车过站工况)的对比参照。隧道总长51.6 m,内径360 mm,截面积约0.1165 m2。图1(b)为8节编组的A+型标准地铁列车模型,总长9253 mm,宽150 mm,高207 mm。图1(c)为站台模型,长11.6 m,宽1.4 m,站台两端隧道部分截面尺寸为0.40 m×0.24 m。列车在隧道中的阻塞度为26.67%,在站内行驶时阻塞度为32.38%,这2种阻塞度与地铁列车实际运行时一致。

图1 动模型试验装置图Fig.1 Photograph of the moving model
图2为全隧道模型和隧道-站台模型的测压点布置示意图。其中,模型中段11.6 m(与站台模型等长)以亚克力透明材料制作,两端各20.0 m以非透明PVC材料制作。如图2(a)所示,全隧道模型共布置24个压力传感器(打孔安装于隧道内壁),依次为1~24号测点。两端非透明段分别布置9个压力传感器(测点1~9、16~24),间距均为2500 mm。透明段中部有一个正方形截面的区间泄压井,泄压井截面尺寸250 mm×250 mm,高90 cm,与隧道轴线垂直,最底端与隧道正上方内壁面平齐。泄压井处压力变化较大,对测点适当加密,其中心处布置1个测点(测点13)、前方(以图中右方列车行驶方向为前方)布置2个测点(14、15号测点)、后方布置3个测点(10、11和12号测点)。压力传感器量程为-3 kPa~+3 kPa,采样频率2 kHz,精度为0.5%;弹射试验系统精度也是0.5%。此外,在隧道入口和出口各布置一个光电门传感器,以监测列车位置,其与屏蔽门的相对位置如图2所示。
隧道-站台模型由入口隧道、站台、出口隧道组成,长度分别为20.0、11.6和20.0 m。出入口隧道部分各设一泄压井,尺寸分别为225 mm×343 mm和370 m×195 mm。进站端设有通风井(关闭状态),尺寸为275 mm×150 mm。图2(b)中的浅绿色矩形表示屏蔽门,其左右两端面为屏蔽门端门,在进站端门处布置1号测点,出站端门处布置5号测点,屏蔽门的侧门沿列车行驶方向依次布置2、3、4号测点(屏蔽门上的测点均布置于靠近列车一侧,高度均为100 mm,即屏蔽门高度中心位置处)。在跟随工况下,对进站端压力测点进行了加密,增加了6~13号测点,如图2(b)所示。
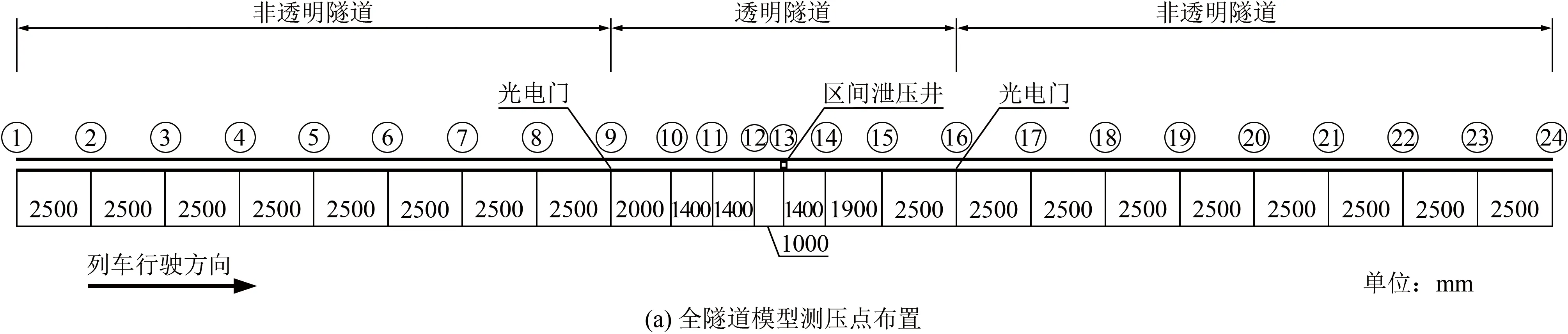
图2 测压点布置示意图Fig.2 Arrangement of pressure measurements
2 结果与讨论
本文讨论单列车经过全隧道模型或隧道-站台模型时的压力波、隧道壁面及屏蔽门上的瞬变压力;隧道-站台模型下列车跟随对屏蔽门上瞬变压力的影响;分析车速、泄压井开/闭对屏蔽门上瞬变压力的影响。为方便起见,t=0对应列车前端进入隧道的瞬间,T1、T2、T3分别对应列车车头进入站台、出站台、出隧道等典型位置的时刻,如图3(a)所示。为保证试验结果正确,所有工况均重复3次。
2.1 过隧道工况
使用全隧道模型开展过隧道工况试验。图3(a)为列车以120 km/h的速度过隧道时压缩波与膨胀波在隧道出入口相互转化的过程(隧道距离为0处,即为隧道入口位置)。图中,红线表示车头位置;蓝线表示车尾位置;黑实线表示压缩波;黑虚线表示膨胀波。图3(b)为隧道中间测点13的压力变化曲线。A点为车头进入隧道产生的压缩波传至测点的时刻,此时压力开始迅速升高。B点为该压缩波在隧道出口转化为膨胀波反射回来到达测点的时刻,此时压力开始降低。C点为车尾进入隧道所产生的膨胀波传至测点的时刻,压力进一步降低。这些微压波在隧道入口和出口反射,强度明显减弱。D时刻为车尾产生的膨胀波在隧道出口转化为压缩波反射回来经过测点的时刻,此时压力略有增加。D时刻至车头到达测点的E时刻,压力基本不变。E时刻后,车头经过测点,压力急剧减小,这与文献[10,26]给出的规律一致。F点为车尾经过测点的时刻,压力出现极小值。列车通过测点后,压力逐渐恢复为零。
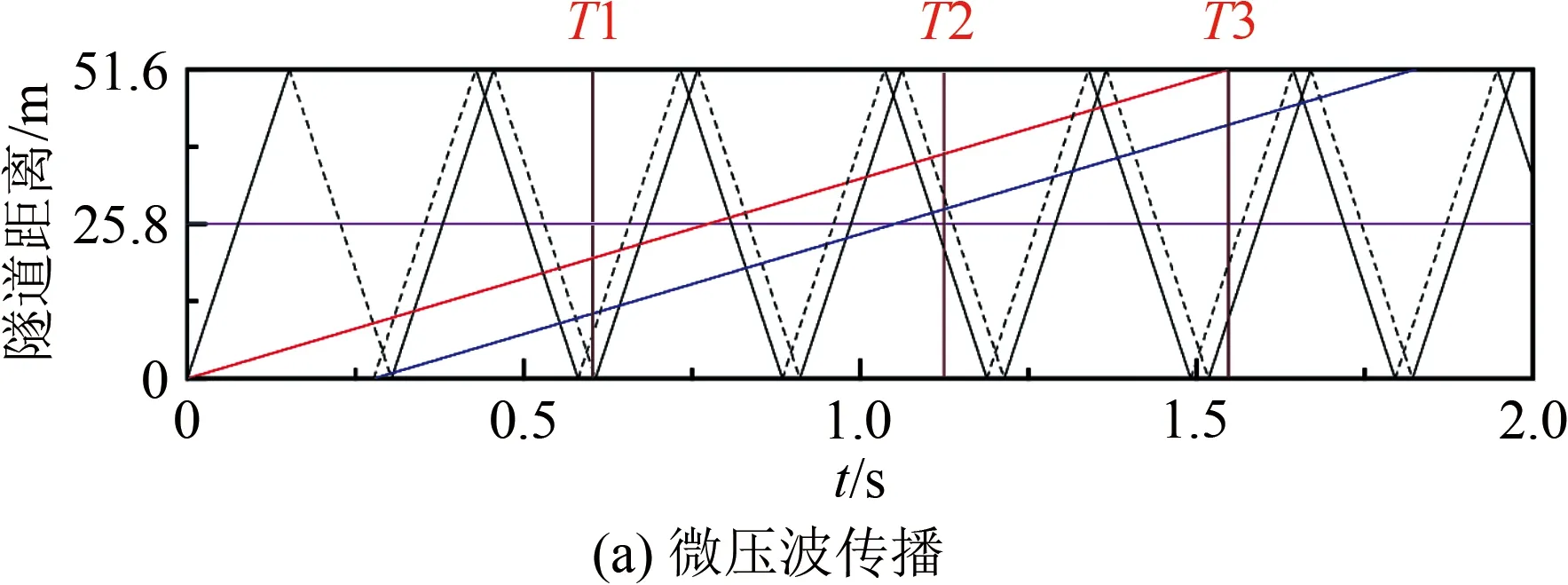
图3 列车以120 km/h速度过隧道Fig.3 Train passing through a tunnel at a speed of 120 km/h
图3(c)、(d)分别为隧道中部泄压井关闭和开启时、列车以120 km/h速度过全隧道模型的各测点压力变化曲线。当泄压井关闭时,各测点的风压变化规律与图3(b)一致。当泄压井开启时,各测点的压力极值显著降低;此外,车头过泄压井时,在隧道中产生一新的压缩波,其传播规律与列车进入隧道时所产生的压缩波一致,但压力极值略小于后者,如图3(d)所示。
为分析车速与泄压井对隧道风压极值的影响,图4给出了不同车速下各测点的压力极值。由图4(a)可知,当泄压井关闭时,随着车速增大,隧道压力极大值增大,且均发生在列车全车刚好完全进入隧道时(通过计算可知,压力极大值出现的时刻刚好对应列车完全进入隧道的时刻)。当车速为140 km/h时,正压力极值为1337 Pa。由图3(c)可知,当测点出现极值时,车头尚未到达该测点,该极值为隧道入口压缩波所致。当泄压井开启时,其附近压力极值明显减小。
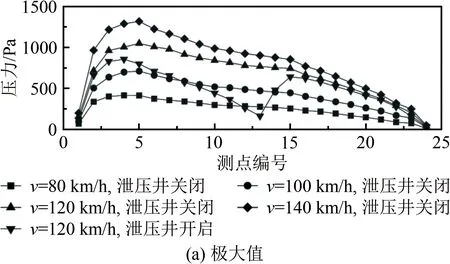
图4 全隧道模型隧道内各测点压力极值Fig.4 The extreme values of the pressure along the tunnel
2.2 过站台工况
使用隧道-站台模型开展过站台工况试验。图5(a)~(c)为站内泄压井开启状态下、列车以不同速度过站时屏蔽门各测点的压力变化。随着车速增大,屏蔽门风压极值呈明显增大趋势,与文献[10,24-26]规律一致。值得注意的是,车速为120 km/h时,屏蔽门各点压力在t=0时就会突增,在0.3 s左右达到极大值285 Pa,该压力极值为压缩波传播到达所致。1~5号测点极值递减,这是因为压缩波传播逐渐衰减[4,29]。从图5(c)可以看出,压缩波在屏蔽门上引起的风压会持续一段时间(压力维持在150~220 Pa左右),直至车头经过屏蔽门时出现另一压力极值(383 Pa,2号测点)。图5(c)中测点的第一个极值由压缩波决定,而第二个极值由压缩波和列车风共同决定。
当站内泄压井关闭时(车速120 km/h),如图5(d)所示,压缩波在进站端门上引起的压力显著增强,最大值为555 Pa,与泄压井开启时端门上的压力相比,增幅约44.9%;此时,屏蔽门侧门上的压力极值为516 Pa,增幅约34.7%。值得注意的是:当列车以120 km/h车速过站、站内泄压井开启时,屏蔽门上压力极小值为-292 Pa,屏蔽门上压力极值的变化幅值为675 Pa;而当泄压井关闭时,压力极值变化幅值增加到1050 Pa(压力极小值为-495 Pa),该工况对屏蔽门强度和疲劳更为不利。
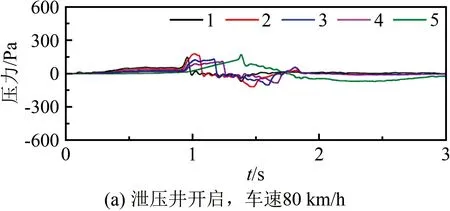
图5 屏蔽门压力Fig.5 Pressure on the PSD
2.3 跟随工况
使用隧道-站台模型开展跟随工况试验。随着发车频次增大,跟随工况在地铁运营中越来越常见,而屏蔽门开闭故障也多发生于此工况。本文跟随工况主要针对站内停靠一辆列车、屏蔽门无法正常开闭、而跟随车辆正向站内行驶的情况。以轻质泡沫板制作了与列车缩尺模型外形尺寸相同的简化列车模型,将该模型中点对准站内中心位置(即13号测点位置)固定,列车靠近站台的侧面与屏蔽门侧门的距离为45 mm,用于模拟站内停靠车辆的阻塞效应。跟随车辆仍以120 km/h的速度进入隧道,与泡沫列车模型相撞后继续向前驶离站台。利用光电传感器可确定跟随列车位置,仅提取跟随列车驶入隧道至碰撞前的部分进行分析。
图6为跟随工况下、站内泄压井开启时屏蔽门上各测点压力的变化曲线。该图截止时刻为跟随列车到达进站端门的时刻(即两车发生碰撞的时刻,非真实运营状况)。可以看出,在大约t=0.35 s时刻,进站端门压力极大值为365 Pa,侧门压力极大值为345 Pa,侧门不同位置的压力极值随着与进站端门距离的增大而减小。极大值之后,列车过区间泄压井时产生的压缩波传递至屏蔽门,屏蔽门端门风压降至300 Pa左右,侧门风压降至约270~160 Pa(沿站台方向逐渐降低),且该压力会持续约5 s(按1∶20折算的真实时间)。这一持续风压很可能是站内停靠车辆时屏蔽门无法正常开闭的主要原因。当两车极其接近时,屏蔽门风压会再次迅速增大,但这一情况在现实中不会发生。
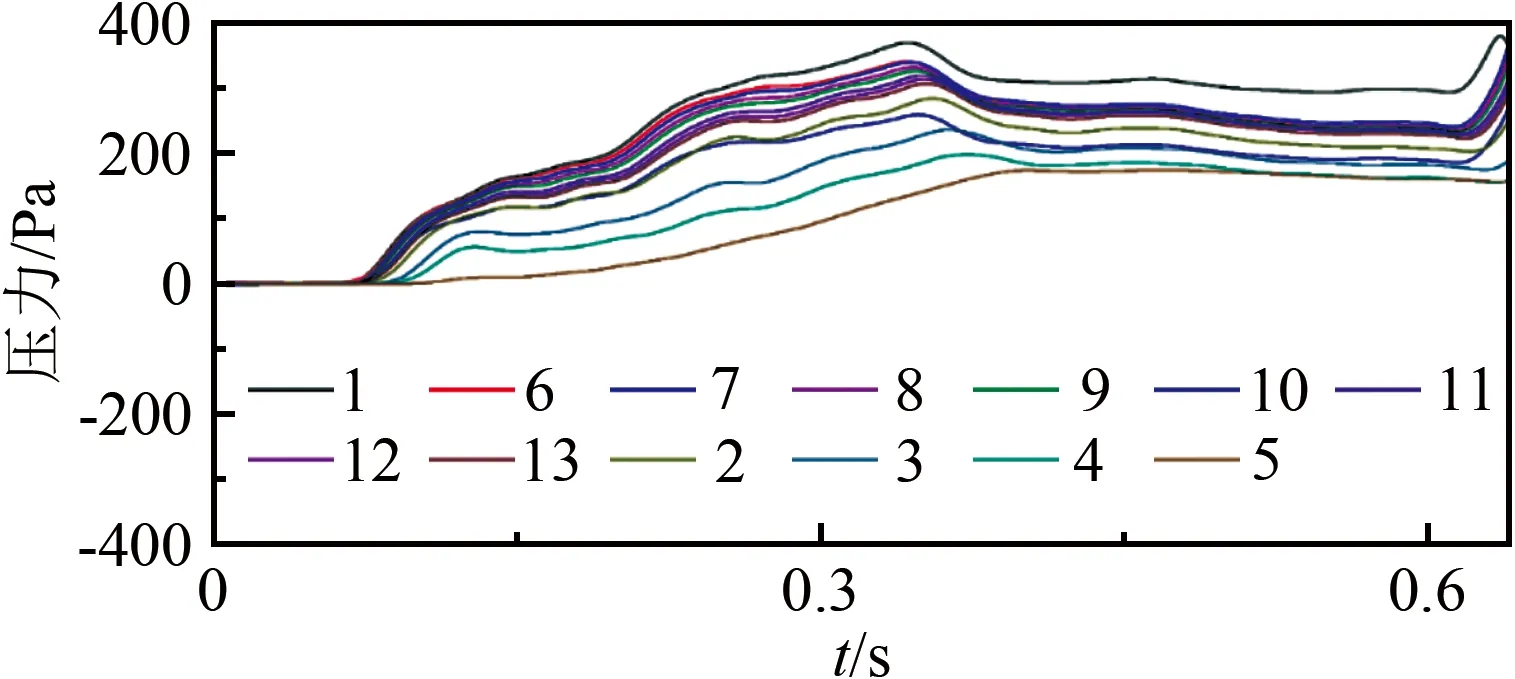
图6 跟随工况下的屏蔽门压力Fig.6 Pressures on the PSD for tracing case
图7横坐标表示屏蔽门上的压力测点与进站端门的距离,横轴最左端对应测点1位置(即进站端门位置),横轴最右端对应测点5位置(即出站端门位置);图中黑色方形表示跟随工况下的风压极值,黑色圆形表示列车过站工况下的风压极值。从图中可以看到,屏蔽门风压极值沿行车方向逐渐减小。对比跟随工况与过站台工况,可以看出两者的屏蔽门压力极值变化规律非常相似;在跟随工况下,站内有车停靠,阻塞度增大,屏蔽门风压极值有所增大。
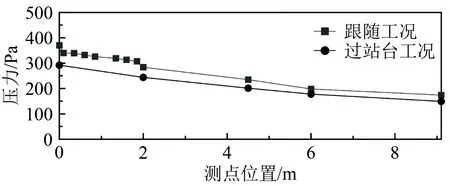
图7 跟随工况、过站台工况下屏蔽门风压极值沿站台变化规律Fig.7 The extreme pressure along the PSD for tracing and passing platform cases
3 结 论
通过动模型弹射试验研究了列车过隧道、过站台以及跟随工况下隧道内风压与屏蔽门风压的变化规律,对比了不同行车速度、泄压井开闭状态对风压极值的影响规律,得到以下结论:
(1) 列车过隧道工况下(全隧道模型),隧道内壁面风压随车速的增加而增大。区间泄压井开启时,其附近的风压极值显著降低。列车通过区间泄压井时也会产生一压缩波,其特性与列车进隧道时所产生的压缩波类似,但风压极值略小。
(2) 列车以120 km/h速度过站台时,屏蔽门风压会出现一个明显的由压缩波引起的峰值,且由于压缩波的影响,屏蔽门上的风压响应会在150~220 Pa维持一段时间,其在屏蔽门上引起的风压最大值约383 Pa。泄压井关闭时,屏蔽门风压最大值为555 Pa,增幅约44.9%。
(3) 列车过区间泄压井时产生的压缩波传递至屏蔽门后,压力极值将会保持在300 Pa左右并持续约5 s,这一侧向压力是导致屏蔽门无法正常开闭的主要原因;无论是列车过站还是列车跟随,压缩波引起的屏蔽门上的风压响应均沿行车方向逐渐减小。
