基于凸松弛优化算法的机器人手眼标定

张亚如，杜建宾,2

（1.廊坊师范学院，河北 廊坊 065000；2.天津大学，天津 300072）

0 引言

1962 年世界上第一台MArobotUNIMATE 诞生以来，随着科学技术的迅猛发展，机器人已经逐步进入我们的社会生活中，其中研制机器人成为国家或地区科技水平体现的重要方面［1-2］。机器人视觉处理的一项基本目标就是手眼标定，目的是估计变换矩阵，这个矩阵是指机器人末端执行器上搭载的相机坐标系到执行坐标系，而且是许多高级机器人的基本任务，因此手眼标定的研究非常重要。

自1989 年Tsai［3］和Shiu［4］首次提出手眼标定问题以来，国内外研究学者对此问题做了大量研究，根据标定矩阵的求解顺序可以将手眼标定问题的求解算法分为两大类。第一类是先解决旋转矩阵再找出平移向量：如1991 年，Chou［5］提出一种基于单位四元数的闭环线性解法；1994年，Park［6］结合欧氏运动群SO（3），提出一种改进的方程式求解算法；2008 年，Malti［7］针对医用内窥镜辅助治疗中的手眼标定问题，提出一种基于对偶四元数理论的手眼标定矩阵求解方法；2015年，王金桥［8］提出利用遗传算法解决关节臂视觉检测系统中的手眼标定问题。这类算法适用于旋转矩阵估计精度较高的情况。第二类是旋转矩阵和平移向量同时求解：如1999年，Daniilidis［9］提出基于对偶四元数和螺旋理论的手眼标定方程求解算法；Andreff［10］针对标定小范围移动的测量场景，提出一种基于矩阵直积的手眼标定方程闭环解法；2011 年，Zhao［11］提出一种基于∞-范数优化模型的手眼标定算法；李巍［12］结合RANSAC 算法对夹角预定数据进行预筛选，利用凸松弛全局优化算法来解决这个问题。这类算法基于四元数理论由于旋转矩阵和平移向量一起解耦计算，其中误差直接影响旋转矩阵的求解精度，因此适用于平移向量误差较小的情况。

以上算法通过不同的轴角变换、单位四元数等来寻找矩阵，标定矩阵是通过最小化代数误差找到的。但是由于敏感的代数误差（相对测量噪声），在误差较大的情况下容易收敛到局部最优解，影响转换矩阵的具体精度。

针对上述问题，本文提出针对对偶四元数模型的手眼标定凸松弛优化算法，该算法将旋转矩阵和平移向量分开求解，并利用以目的为导向的误差评价方法，提高手眼标定关系的标定精度和可靠性。

1 机器人手眼标定模型

参照Tsai［3］的手眼标定数学模型，设P1，P2代表变换矩阵（靶标世界坐标系到两个不同姿态的摄像机坐标系），Q1，Q2代表为两次不同的变换矩阵（机械手末端执行器坐标系到机械手基坐标系），X代表摄像机坐标系到机械手末端执行器坐标系，则手眼关系可以表示为式（1）：

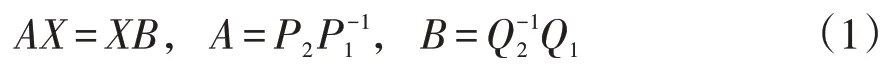
其中，A、B、X都为4×4的矩阵，将上式展开可以解耦表示成只含有旋转矩阵R和平移矩阵T的方程形式为：

将对偶四元数aˉ,bˉ,qˉ展开为实部和对偶部四元数的形式，应用四元数乘法可以将（2）、（3）中的旋转平移部分用对偶四元数的实部和对偶部分别表示为：

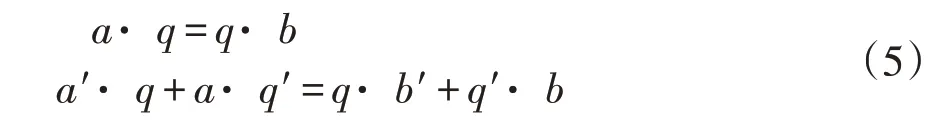
1.1 手眼变换矩阵中旋转矩阵R的求解

先考虑旋转方程a·q=q·b 中的实部q 求解，其中a，b，q分别表示旋转矩阵RA,RB,RX所对应的单位四元数，将（5）式代入上述旋转方程并利用四元数乘法合并整理可得:

其中，I3表示为3×3单位矩阵，K（a，b）表示由单位四元数对（a，b）所确定的4×4的矩阵。假设n（n≥2）次位姿变换测量得到K（ai，bi），构建4n×4 矩阵L=［K（a1，b1），K（a2，b2），…，K（an，bn）］，则旋转矩阵R 对应的四元数q 可以由矩阵L 奇异值分解求得。

1.2 手眼变换矩阵中平移矩阵T的求解

再考虑平移方程a′·q+a·q′=q·b′+q′·b中的对偶部q′求解，利用四元数的乘法性质以及式（6）的表示形式，关于对偶四元数的对偶部q′的标定方程可以化简表示为：

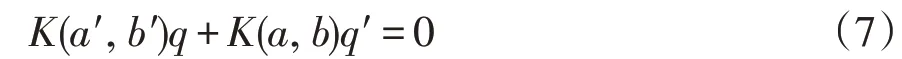
将（7）转化为线性方程组：

对偶四元数的正交性，将方程组（8）变换成带有约束条件的最小二乘问题：

其中，||.||2表示矩阵的2 范数，利用Levenberg-Marquardt 非线性优化算法对上式求解即可得到对偶部q′，再利用对偶四元数中对偶部与实部的转换关系式（8）即可得到手眼变换矩阵X 中的平移向量tx，从而得到表示手眼关系的变换矩阵X。

2 凸松弛多项式优化方法

利用文献［7］中的非线性优化算法式（9）中最小二乘问题能较快地收敛到最优解，这个问题自带约束性。但准确性取决于对偶部q′初值的选择，且存在收敛到局部最优解，不能保证每次全局最优解都能收敛找到。启发式的全局优化算法例如蒙特卡罗采样法、神经网络等基本通用，但具体案例中需要规划众多参数和算法设计以提高执行效率，而基于LMI 松弛技术的优化专门针对特性的凸松弛多项式优化问题，不需要初值估计，从理论上讲，LMI 方法是其中最可靠的选择，可以最大限度地保证计算寻优到全局最优值［14］。因此本文将手眼变换矩阵中的优化问题转化为凸松弛多项式优化问题从而去求最优解。

首先，利用奇异值分解式对偶四元数的实部q进行运算，然后，以单位对偶四元数的正交性为约束限制，建立关于式（9）的多元多项式优化问题：

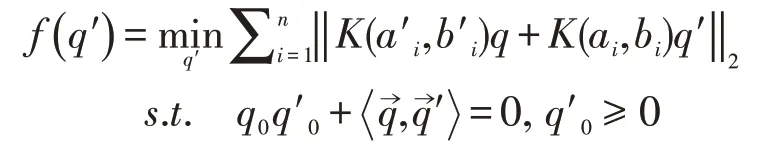
至此求解多项式函数优化问题的等效问题，就是半正定规划，那么采用Lasserre 非凸函数LMI 求解，经计算得知，由70个单项式组成的2元4次目标函数f 为多项式函数，增加约束条件q′0≥0 是为了避免求解过程中出现2 个全局最优解的情况，增加约束条件q′Tq0=0 是为了保证对偶四元数求解结果的正交性，确保半正定规划限制内的点求解的数值稳定性。

利用Henrion 发布的GloptiPoly3 软件包进行算法计算［15］，Henrion等人率先把LMI加入到计算机视觉中解决多视图几何下的三维重建问题的办法之中［16］。国内，肖永亮［17］及柯丰恺［18］将其引入解决相机的内外参数标定问题。本文也采用此方法解决基于对偶四元数模型下的手眼标定矩阵优化问题，LMI难点在于优化的目标函数转化为半正定规划问题求解的具体操作。

3 实验结果与分析

为了验证所提出算法的可行性与优化精度，搭建模拟实验平台，利用Matlab Camera Calibration Toolbox 工具箱标定相机得到不同位姿下的相机外参数Pi（i=1，…，N），并将其交叉混合计算整合获得新的M=N（N+1）/2组手眼标定数据集{Pi+1（Pi）-1，（Qi+1）-1Qi}，最后，分别使用本文提出的凸松弛优化估计（Convex Relaxation Optimization，CRO）、文献［7］中的非线性优化分步估计（Nonlinear Optimization Separated，NOS）和文献［9］中的非线性优化同步估计（Nonlinear Optimization Homochromous，NOH）手眼标定算法对机器人的手眼关系进行标定，结果分别记为XCRO，XNOS，XNOH。由于实际标定的真值无法得知，因此为了评价和比较3 种估计算法的精度，采用以目的为向导的评价模式，即根据标定手眼关系矩阵X和变换矩阵（运动模型为原型）Bi逆求解相机运动变换矩阵估计值Âi，并将其值与经过相机标定得到的相机运动变换矩阵Ai的值进行比较分析。

实验中，每次移动机械手筛选出M=16 组标定数据{Aj，Bj}（j=1，…，16），分别使用上述3 种不同的算法（CRO，NOS，NOH）通过前8组标定数据计算手眼变换矩阵X，在同一标定数据集下，3 种算法得到的手眼变换矩阵分别为：

10组完全独立的手眼标定实测实验中3种不同的算法（CRO，NOS，NOH）的手眼标定旋转和平移误差比较见图1所示。

图1 实测实验旋转和平移绝对误差比较

图1中，每一种算法采用10个点代表10次手眼标定实验的旋转和平移绝对误差结果，距离原点的位置远近和误差大小对应，可以看出，从旋转和平移的可靠性稳定性精确度看，NOH算法的精度和稳定最差；CRO和NOS算法手眼标定计算中将旋转矩阵和平移向量分开求解，位置误差较大的情况下，仍靠近原点，具有高精度和分布集中性。10组重复测试中（如图1），CRO 算法的旋转矩阵绝对误差最大值为0.035mrad，比NOS小0.002mard，平移矩阵绝对误差最大值为1.315mm，比NOS的小0.019mm，从误差数值可以看出CRO算法略优于NOS。

4 结论

鉴于机器人运动学正解及Camel外参数标定必然出现数据的偏向差别，因此局部最优解存在手眼标定优化问题中。本文在对偶四元数概念之上采用一种基于凸松弛优化技术的手眼标定算法。该算法优点是初值不需预估，可以最大限度确保获得最优解，从而规避寻优过早陷入局部解。实测结果表明，提出的凸松弛优化算法（CRO）较传统的非线性优化手眼标定算法（NOS）具有较高的精度和稳定性，在高精度的机器人视觉系统中具有一定的应用价值。