基于压缩感知理论的分块压缩感知算法
2021-01-12吴亚娟
黄 超,吴亚娟
(西华师范大学,四川 南充 637009)
0 引言
在信息处理领域,传统的信息采集方式一直遵循着奈奎斯特采样定理,即采样率必须大于被采样信号频率两倍才能完整重建信号。但是在一些特殊环境下,无法做到全采样时,奈奎斯特采样定理反而成了阻碍采样行为的壁垒。文献[1]提出是否可以用低于奈奎斯特采样定理规定的两倍采样率采样信号并重建信号。文献[2]正式提出压缩感知理论并指出压缩感知突破的关键在于采样方式。当我们说“采样频率”的时候,是做等间距采样,数字信号领域通常都是做等间距采样,也服从奈奎斯特采样定律。压缩感知则不同,压缩感知采用的是不等间距采样,因此随机的亚采样给予了恢复信号的可能性。随机采样使得信号频谱不是整齐的平移,而是一小段一小段地随机迁移,频率泄露均匀地分布在整个频域,所以泄露值都比较小,从而有了恢复的可能。
基于压缩感知理论,诞生了许多不同的压缩感知算法,但大致可以归结为压缩感知体系的三个部分:非稀疏信号的稀疏表达Ψx、稀疏后信号的观测y=ΦΨx、观测值的重构。由于待观测信号事先是未知的,所以稀疏基的选取和观测矩阵的选取就直接决定了重构算法是否能够完整重构信号。重构时传入的信号分别是观测值y,稀疏基Ψ,观测矩阵Φ。而观测矩阵和稀疏基一般结合使用称为信息算子或者传感矩阵ACS=ΦΨ。
目前大多数的压缩感知算法针对观测矩阵和重构算法的研究都是对一维信号进行的压缩观测和重构[3-5],不适用于处理大规模二维数据。针对这个问题,文献[6]提出了一种改进的压缩感知算法以用于处理二维信号,在解决二维数据无法直接运用压缩感知处理的问题上有明显效果。本文提出一种分块存储按列恢复的算法,并加入传感矩阵的不相干性判断,相比于不分块的压缩感知和文献[6]提出的简单分块压缩感知,本文算法平均运行时间更短、图像恢复精度更高、观测矩阵占用空间更小。
1 压缩感知及重构算法
1.1 稀疏性
压缩感知也可以叫做感知压缩,即直接感知压缩后的信号。基本理论支撑来自TAO[7]及Candes[8]从数学上证明的RIP 原则:即如果信号是稀疏的,那么它可以由远低于采样定理要求的采样点重建恢复。
考虑到自然界中的一些非稀疏信号,需要作稀疏变换,使信号近似满足稀疏性。若一个信号x 为非自稀疏信号,只要信号x 在某一个变换域满足近似稀疏性,就可以在这个变换域中把x 看做稀疏信号,即可压缩信号。我们称这种变换域为稀疏域,重建将在稀疏域进行。这样,压缩感知就可应用于自稀疏信号与非自稀疏信号。
设x 是信号,Ψ 是稀疏基,θ 是x 在Ψ 中的稀疏。x 的稀疏表示为:

Ψθ 称为x 的稀疏表示,当x 是本身稀疏时,稀疏基Ψ 就可以是单位阵,即X 本身自稀疏。当X是非稀疏信号时,稀疏基可以是离散傅里叶变换阵、离散余弦变换阵DCT、离散小波变换阵DWT 等常用频域转换矩阵,也可以是基于冗余字典的扩展稀疏阵[9-10],还可以是其他针对特定信号的确定性矩阵。
1.2 观测矩阵及RIP性质
合适的观测矩阵是重构质量的前提保障,选择合理有效的观测矩阵可以保证重构质量以及高概率重构信号。观测矩阵一般分为三种类型,高斯/伯努利型随机测量矩阵,傅里叶/小波测量矩阵及衍生矩阵,其他测量矩阵如局部哈达玛矩阵、Toeplitz 循环矩阵等确定性矩阵。
设y 是观测值,观测阵为Φ,稀疏基为Ψ ,信号为X。则x 的观测值为:

公式(1)对应亚采样过程,它将高维型号x 投影到低维空间。y 是一维的测量值,也是亚采样后的结果。
因此,压缩感知问题就是在已知测量值y 和测量矩阵Φ 的基础上,求解欠定方程组y=Φx 得到原信号x。一般的自然信号x 本身并不是稀疏的,需要在某种稀疏基上进行稀疏表示。令x=Ψs,Ψ 为稀疏基矩阵,s 为稀疏系数。
于是最终方程就变成:y=ΦΨθ ,已知y、Φ、Ψ,求解θ。
当采集未知信号x 时,不可能事先对信号进行预稀疏化处理,所以稀疏基Ψ 一般在重建过程与观测阵Φ 同时使用,令ACS=ΦΨ ,则ACS称为信息算子或传感矩阵。
Tao 等人证明[7],观测矩阵需满足RIP 性质,即约束等距性。RIP性质如下:
对于任意和常数有:
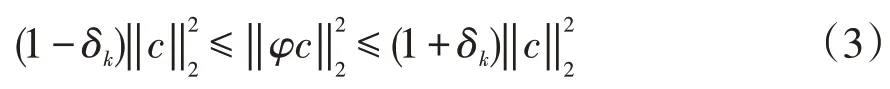
然而,对于处理图像的观测矩阵来说,要去判断其完整的RIP 性质满足与否,是比较困难的,随后,Baraniuk 证明,RIP 等价条件是观测矩阵和稀疏基不相关。
相关性定义:
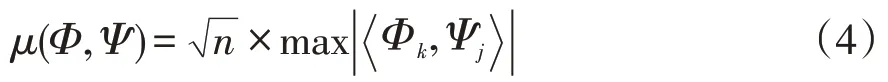
μ 越小,Φ 和Ψ 越不相关,等价于RIP 性质越满足,则重构信号效果越好。
1.3 重构算法
在获得线性观测值之后,将观测值y 和传感矩阵ACS传入重构算法中,以求得x 在Ψ 中的稀疏系数θ,则可以通过x-Ψθ 重构信号。目前重构算法多种多样,大致可以分为三类:基于数学上求解l1范数[11]的凸优化类算法,比如BP 算法、内点法[12],此类算法优点是重构精确度高,但是算法比较复杂难以硬件实现;基于MP 贪婪算法求解的衍生算法[6],此类算法精确度不如凸优化类算法,但是优点是便于实现和求解概率较高;其他组算法,比如傅里叶采样、链式追踪等。
本文算法均采用OMP算法作为重构算法,采样率为0.5进行实验对比,保证重构算法为不变量,并使用不同尺寸的lena 图像进行观测和重构以研究算法在不同尺寸图像观测和重构时的性能。
算法步骤:
Step1 初始化x 为N=256 长度的信号,稀疏度K=30,x 的K 个位置随机赋值1,其余位置为0,x 为一维离散稀疏信号
Step2 初始化观测阵phi,初始化稀疏阵psi,初始化恢复向量x_r
Step3 观测,y=phi*x
Step4 重构,此处用OMP 算法重构信号,求得θ,x_r=psi*θ
Step5 绘图,计算残差
测试不同大图像对比结果如表1所示。
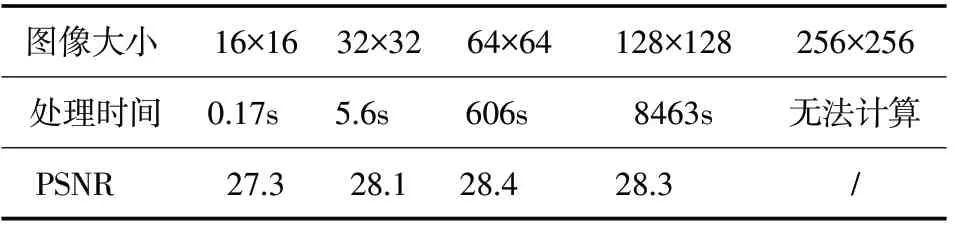
表1 随机矩阵采样率0.5,i7-10700k,32G,matlabR2017平台
2 压缩感知实现
2.1 一维信号
由图1 可以看出,在K=30 时,当采样率大于或者等于0.5以后,信号就能完整恢复。
由图2可以看出,在采样率P=0.5时,稀疏度K在大于或者等于30以后,开始出现信号恢复出错的情况。
以上每个点数据都是测算10次后取的平均值,几乎不存在偶然性,可以看出,对于一般一维稀疏信号,压缩感知还是比较有效的,采样率可以远低于2倍采样并且精确重构信号。
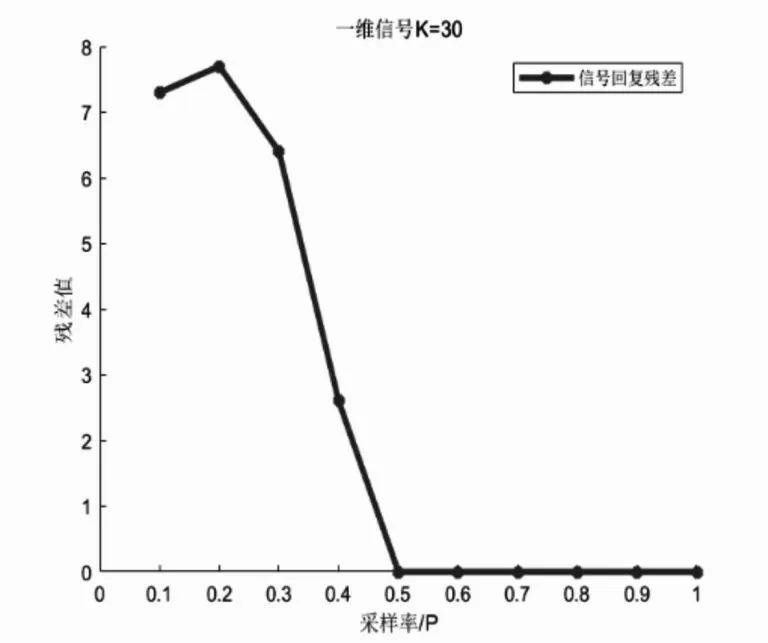
图1 一维信号

图2 不同采样率下残差
2.2 二维信号
如果用处理一维信号的压缩感知来进行二维信号的处理时,会由于信号长度过大而导致观测矩阵过大、恢复重构时间过长甚至不可处理一系列问题。处理二维信号的通常方法是将二维图像矩阵变形成一维向量再进行观测处理,这样会导致数组爆炸,从而只能处理很小的图像,或者对计算端的计算能力需求太大而不具实际意义。
不分块的压缩感知在处理不同大小图像时的表现如下:用一般处理一维的方法处理二维图像,处理时间近乎指数级增长,而且由于单次求解元素太多,导致精度难以得到保证,显然不利于实际使用和实现。
2.3 分块压缩感知
分块压缩感知的提出是为了解决当图像数据较大时,观测矩阵占用内存太大和重建过程时间太长而提出的。运用分块处理降低数据规模,把原始图像分成若干大小相同的小块,对每个小块进行采样和压缩传感,最后重构每个小块至整个图像,完成压缩传感重构。这种方法的优势就是对每个小块进行独立测量,可以有效控制每次测量处理的数据规模,使用较小的观测矩阵和传感矩阵,保证算法运行时间不会随图像增大呈指数级增长,将算法运行时间控制在可接受范围。
简单分块算法步骤:
Step1 输入图像X,将X 按bn*bn大小进行分块,bn=8
Step2 对分块循环执行观测操作,观测矩阵维数为bn*bn
Step3 对分块循环执行
重构算法,将恢复的块依次拼接到待恢复矩阵X_r
Step4 重构X_r,计算PSNR
测试不同大小图像后对比结果如表2所示。
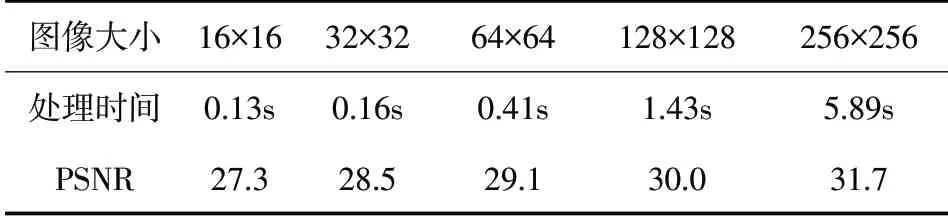
表2 随机矩阵采样率0.5,i7-10700k,32G,matlabR2017平台
由表2 可以看出,分块压缩感知对算法速度的提升很大,并且可以处理超过256×256大小的图像,算法运行时间也在可接受范围内,但是重构质量并未得到提升。分块压缩感知最大的作用就是将二维图像信息变得可处理,从数据来看,常规分辨率图像都在可处理范围,不会出现处理时间随图像增大而近乎指数级增长的情况。
3 算法
3.1 BSP-CS算法
对于上文提到的分块压缩感知,本文提出一种分块存储按列恢复的BSP-CS算法。与上文算法相比,分块存储可以模拟更真实的压缩感知流程,按列恢复可以在二维观测矩阵匹配图像时使用更小的观测矩阵,从而节约观测和重构时间。
BSP-CS算法步骤:
Step1 输入图像X,
Step2 将X按bn*bn大小进行分块,记录每个分块的位置信息bi
Step3 将分的块依次通过观测矩阵测量,将测量值存入yi
Step4 将测量值传到重构端,依次读取传入的观测值yi进行重构
Step5 将重构的图像块通过bi定位到图像位置,更新恢复图像X_r
Step6 重构X_r,计算PSNR
测试不同大小图像后对比结果如表3所示。
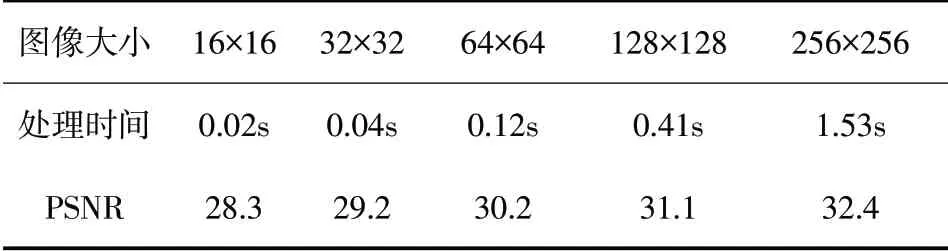
表3 随机矩阵采样率0.5,i7-10700k,32G,matlabR2017平台
由表3可以看出,本文算法运行时间极短,并且重构精度并未减少。相比于不分块的方法,本文算法平均运行时间只有前者的1%,并且不会随图像增大而运算时间陡增。相比于简单分块的压缩感知,本文算法平均运行时间只有前者的20%左右,提升明显。
3.2 BSPI-CS算法
对于BSP-CS只提高了运算速度并未提升重构质量问题,结合压缩感知原理,提出在观测矩阵和稀疏阵的选择时增加RIP 计算步骤,加入对传感矩阵的不相干性判断的BSPI-CS 算法以提高重构质量。由公式(3)可知,如果直接对观测阵进行RIP判断,通常比较困难。于是算法BSPI-CS 选择第二种等效RIP 性质判断方式,对观测阵和稀疏阵进行不相关性判断。由于观测阵和稀疏阵都是预先设计好的,所以很容易判断不相关性。
BSPI-CS步骤:
Step1 输入图像X,
Step2 将X按bn*bn大小进行分块,记录每个分块的位置信息bi
Step3 根据公式(4)对设计的观测阵和传感阵进行不相关性判断,直至得到满足条件的传感矩阵为止
Step3 将分的块依次通过观测矩阵测量,将测量值存入yi
Step4 将测量值传到重构端,依次读取传入的观测值yi进行重构
Step5 将重构的图像块通过bi定位到图像位置,更新恢复图像X_r
Step6 重构X_r,计算PSNR
测试不同大小图像后对比结果如表4所示。
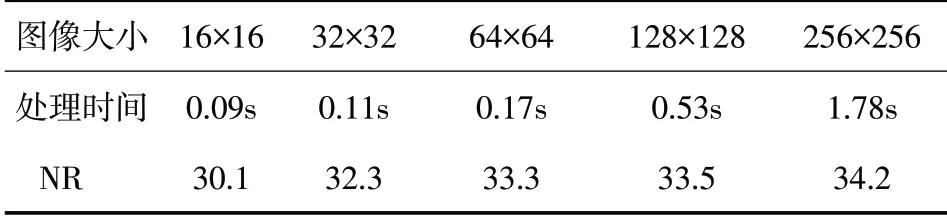
表4 随机矩阵采样率0.5,i7-10700k,32G,matlabR2017平台
由表4 可以看出,因为加入了传感阵不相干性判断步骤,所以平均运行时间有所增加,在算法执行中对观测阵和稀疏阵的选取决策时产生了额外时间,该时间不随图像大小而改变,只是围绕一个固定值上下浮动。根据算法原理可以推测算法运行额外增加的时间是随观测矩阵的大小变化而变化的,当观测矩阵不变时,额外增加的算法运行时间相差甚微。根据PSNR 值可以看出,由于加入了不相干性判断,算法重构图像的精度有了明显提升,一般认为PSNR>30,则重构质量较好。
3.3 实验数据对比
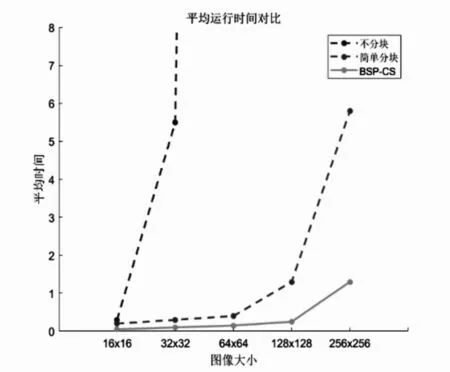
图3 平均运行时间对比
图3是固定采样率为0.5,重构算法为OMP重构算法时,本文提到的各种算法的平均运算时间随图像增大的变化对比。可以看出,分块算法BSP-CS在减少运行时间上效果与简单分块算法相比优势明显。
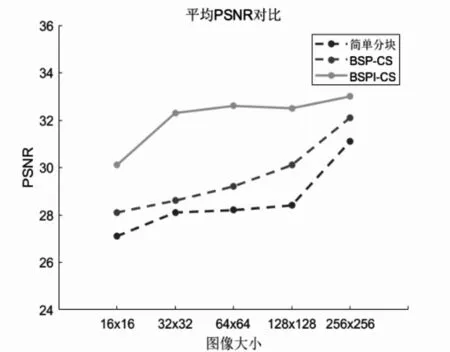
图4 平均PSNR对比
图4是固定采样率为0.5,OMP重构算法时的平均PSNR 对比,可以看出BSPI-CS 算法在牺牲少量算法运行时长的情况下,稳定地提升了图像重构的精度。
4 结语
在研究了压缩感知算法后,本文提出了两种算法,改进了观测和重构运行时间,基于等效RIP性质的不相干性公式在重构算法开始前加入了传感矩阵的不相干性判断,提升了图像重构精度。BSP-CS算法对缩短算法平均运行时间有明显改进,BSPICS 算法则是牺牲一部分算法时间来提高图像重构精度,两种方法都对压缩感知算法改进有一定的作用。
