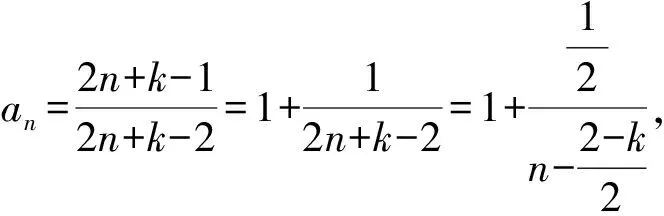例谈单元教学设计下的变式教学探索
2021-01-12李健
李 健
(江苏省外国语学校 215104)
面对不再有考试大纲的“新”高考,深入解读新课标、优化整合知识点成为了每个教育工作者所要研究的新课题.在达成“聚焦学科素养、优化课程结构、把握数学本质”的同时,如何合理高效地规划教学模块,“单元教学设计”成为了一个学界认可的重要着眼点.
高中数学单元教学的目的在于实现整体大于局部之和的教学效果,强调的是数学内容、学生的学习和发展的整体性[1].这就需要在设计单元教学时,突出数学内容的主线,并对具有共同特征和较强关联性的数学内容进行动态地整合和重组.从教学系统论的角度来看,这本身就是一种结构“变式”,其目的也与变式教学所主张的“在动态教学中把握数学本质”相得益彰.下面笔者结合教学实践,围绕“函数单调性”这一核心概念,例谈在“单元教学设计”背景下如何有效开展变式教学.
1 重组单元结构,构建变式模块
“函数单调性”是贯通高中数学课程的一条“大动脉”,根据《普通高中数学课程标准(2017年版)》(下文简称《课标》),必修课程中的“函数的概念与性质”、“指数函数和对数函数” 、“三角函数”以及选择性必修课程中的“一元函数导数及其应用”均对“函数单调性”的掌握提出了明确的要求.结合“数列”的函数背景以及“不等关系”的应用需要,笔者对分布这些章节中与单调性相关的知识碎片进行了统筹重组.
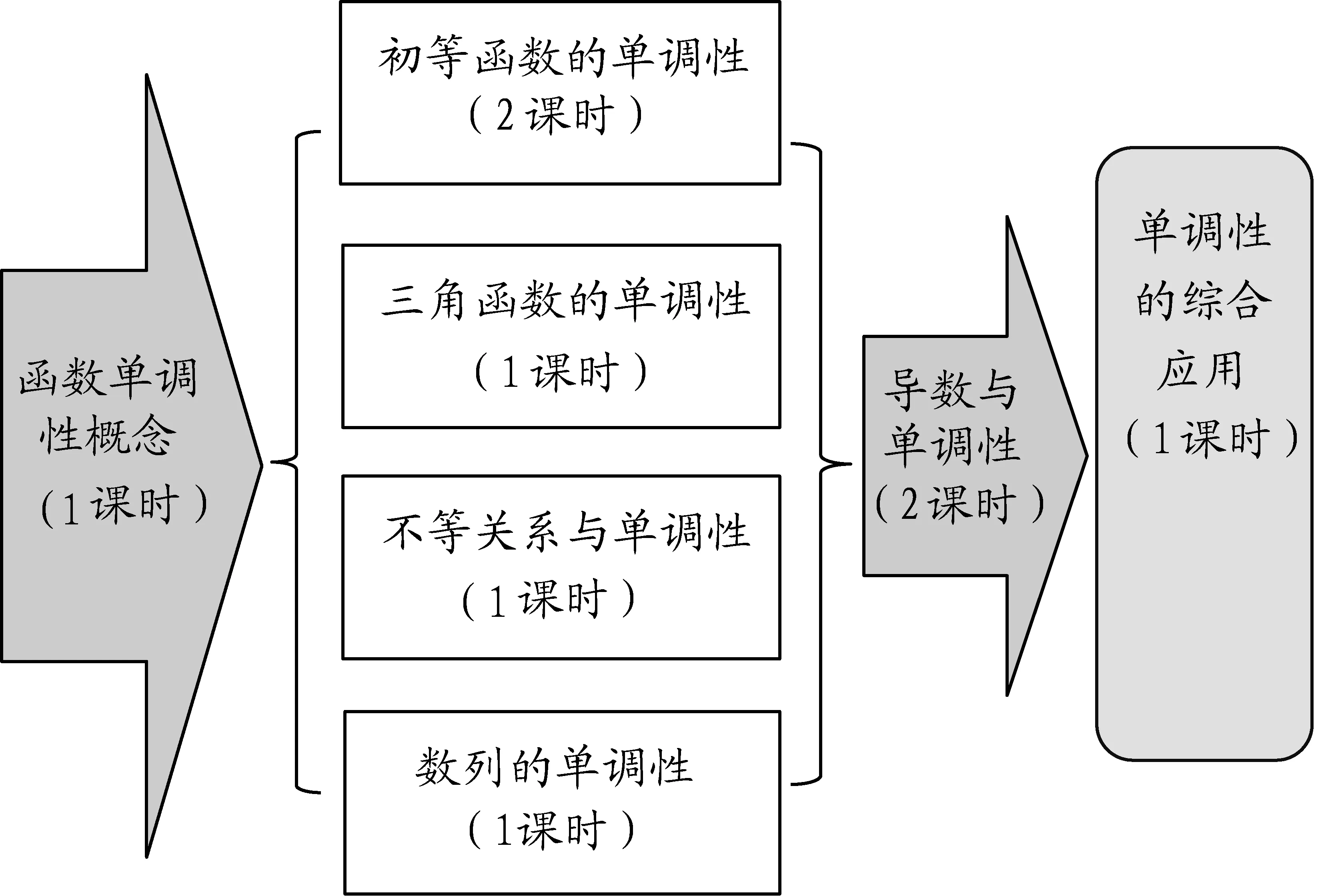
本着基于新课标、定位“新”高考的初衷,针对教学实际,笔者以为高三复习课是最适合现阶段研究的实践落脚点.综合高三学生的知识储备与认知能力,笔者设计了与上述单元结构相匹配的变式教学模块,结构上采用了顾泠沅先生所提出的“过程性变式”,即“数学活动的有层次推进”[2]:首先回顾并熟练掌握函数单调性相关概念,其次以初等函数、三角函数、不等式、数列为载体对其加深理解,进而从导数的视角剖析函数单调性并进行简单应用,最后在综合应用中彰显价值、突出本质.同时,在教学活动逐步推进的过程中,根据每个层次和课时内容特点,有针对性地渗透变式教学.

2 聚焦单元重点,设置变式问题
显然,我们必须根据四个层次对“单调性”的具体教学要求,突出单元的重点内容.例如《课标》在“函数概念与性质”单元要求学生“会用符号语言表达函数的单调性,理解它们的作用和实际意义”.因此,引导学生学会使用“符号语言”理解掌握函数单调性的定义及其内涵是单元的重点内容之一,笔者尝试在“层次一”中设置变式问题,实现这一教学目标.
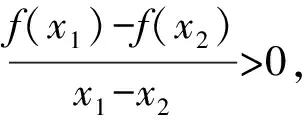
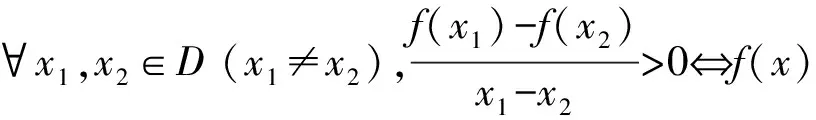
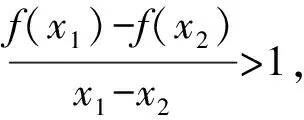
生甲:可得出f(x)在D上是增函数;
师:甲同学的结论是正确的,但只能说明其充分性,你能否找出其充要条件呢?
师:乙同学的思路缜密,他紧扣函数单调性的定义,发现、构造了新的函数,并用符号语言完整展示了探究其单调性的过程,请大家课后据此探究下“减函数”的相关结论.
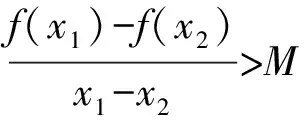
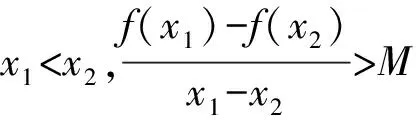
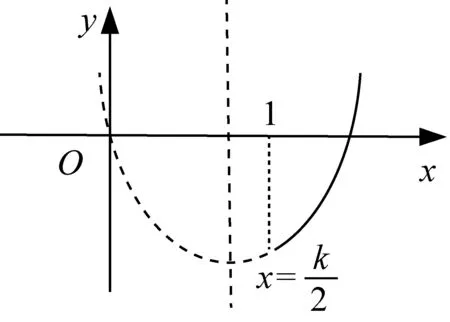
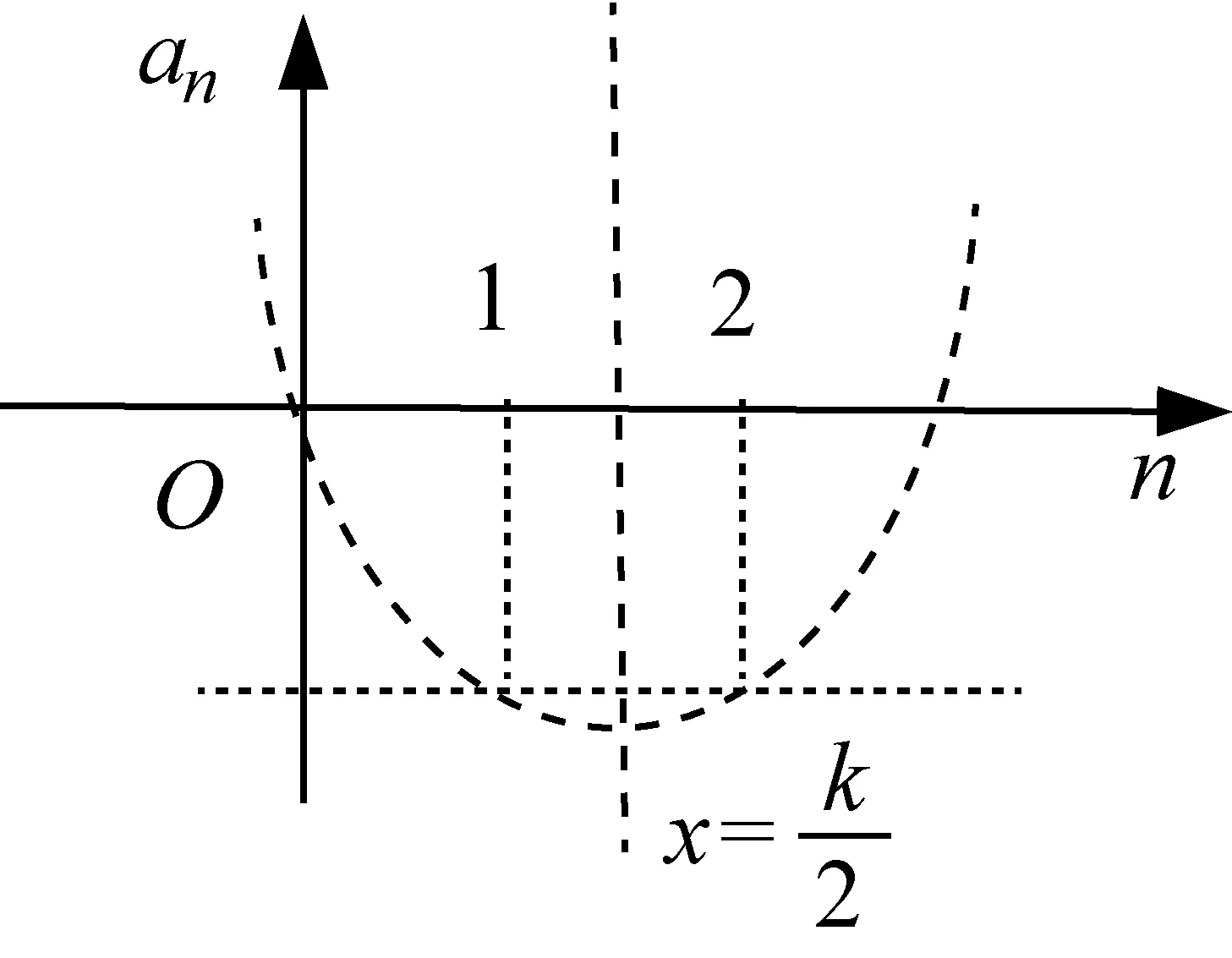
⟺f(x1)-f(x2) ⟺f(x1)-Mx1 ⟺F(x)=f(x)-Mx在R上单调递增, 由题意:F(x)=f(x)-cx=x3+(1-c)x+c在R上单调递增,则F′(x)=3x2+1-c≥0恒成立⟹c≤(3x2+1)min⟹c≤1. 案例反思(1)原题中的“差商”结构本身就是函数单调性定义的一种“变式”,这有助于学生在加深对概念理解的同时提升符号语言的认知表达能力;(2)变题1对学生符号语言的解读能力提出了更高要求,通过辨析差商“>1”与“>0”的逻辑关系与异同之处,让学生在认知冲突中回归定义本源,在探究过程中学会用符号语言完成单调性证明中“作差定号”的过程;(3)通过解决变题2实现了对变题1的学以致用,动态达成了知行合一的目的. 单元教学的核心思想是系统思维[3],单元设计需要我们将原有知识进行重组整合,从整体的高度系统地优化教学过程,例如《课标》在“数列”这一单元中要求“感受数列与函数的共性与差异,体会数学的整体性”,我们可以有效利用“层次二”中“数列”这一载体,将其与函数单调性的相关知识有机整合,通过变式教学达成两者交融理解的“双赢”效果. 案例2师:我们都知道,数列是一种“特殊的函数”,那么是否可以借助于与其通项公式相对应的函数来研究其单调性呢?下面我们通过两组变式问题来辨析和感悟. 变式题组1: (2)已知数列{an}为递增数列,且其通项an=n2-kn,求实数k的取值范围 由(1)中结论,可得(2)中k≤2. 生乙:根据数列单调性的定义,{an}为递增数列⟺an 师:两位同学得出了不同结论,那么谁的答案正确呢? 师:从中我们可以感悟到三点:一、要时刻关注数列“离散”这一特性,二、数列所对应函数在区间D上单调与该数列在区间D内有相同单调性并非充要关系,三、利用单调性的定义是解决这类问题最可靠的方法.接下来请继续思考: 变式题组2: 师:从题组2中,我们不难感悟到:合理利用数列的函数背景可以提高解题效率,与此同时还需考虑其“离散”特性,即转化为研究相邻项的关系来解决问题. 案例反思变式题组1旨在通过研究离散函数的“一阶差分”(简称“阶差”)Δan与连续函数单调性的关系,让学生在“变”的过程中感受思维的碰撞,找出二者差异之处,题组2则是有目的地引导学生从函数的单调性切入,自然感知两者间的共性;且鉴于题组1的实践经历,学生在面对变式题组2时,就会较为谨慎地将对应函数的单调性转化为阶差Δan的正负来研究,自然感悟连续函数与离散函数的异同之处,这都体现了数学的类比思维与应用思维.此外,笔者还从提升学生形象思维的角度探析了上述问题,本文将在随后篇幅中阐述. 《课标》要求“能利用导数研究函数的单调性”,事实上,“感受导数在解决单调性问题时的工具作用”与“深化认知单调性的相关概念”可以双线并行,笔者有针对性地在“层次三”中设计了如下变式. 案例3已知函数f(x)=lnx-ax2-2x(a≠0)在[1,3]上单调递减,求a的取值范围. 师:通过导数这一“犀利”的工具,我们可以很方便的将“在区间D上单调”的问题转化为 “导函数f′(x)≥0(或f′(x)≤0)在区间D上恒成立”问题,从而再转化为更利于解题的最值问题来处理,其中“参变分离”是我们解决这类问题的重要手段. 变题:若f(x)=lnx-ax2-2x(a≠0)在[1,3]上存在单调递减区间,求a的取值范围. 师:“在区间D上存在单调区间”本质上是“能成立”问题,即“当x∈D时,导函数f′(x)>0(或f′(x)<0)能够成立(有解)”,同样可以化归为最值问题来处理. 案例反思该变式实际是利用“一题多变”来铺设教学思路,通过整合单调性和导数的相关知识,引导学生将问题转化为 “恒成立”、“能成立”问题,动态辨析了其中“充分和必要”的逻辑关系,最终再化归为函数的最值的问题来处理,在渗透“转化和化归”的思想的同时,有效提升了学生的逻辑思维能力. 《课标》中,“函数概念与性质”、 “指数函数和对数函数”这两个单元都提出了“借助图像”来研究单调性的要求;“三角函数”单元要求“用几何直观和代数运算的方法研究三角函数的单调性等性质” ;“导数”单元则明确了“借助几何直观了解函数的单调性与导数的关系”的要求[4].针对其共同要求,可以在“层次四”中利用变式,从几何角度重新审视上文中的部分案例. 以案例1原题为例,根据高三学生的认知程度,可以引导学生从“形”的角度思考. 生:斜率,具体来讲就是“函数f(x)图像上两点所连割线的斜率”; 师:请结合“割线斜率”的概念,从“形”的角度理解并描述该问题你所得到的结论; 生:函数在区间D上任意两点所成割线的斜率为正⟺函数在D上单调递增; 师:实际上,我们从“数”的角度出发,可以进一步理解为“区间D上任意两点的平均变化率的正负决定了其在区间D上单调性”.大家可以将问题中的“任意性”和“瞬时变化率”的概念相结合,从导数几何意义的角度深入理解其和单调性间的关系. 同样在案例2变式题组1(2)中,我们如果选择延续生甲的思路,通过剖析对比f(x)=x2-kx,x∈[1,+)和an=n2-kn,(n∈N*)的图像,就会发现甲同学是因忽略了数列离散的特点而忽视了a1 图1 图2 图3 直观想象的培养应该贯穿在整个高中数学教学的全过程[5],针对理解“单调性”概念对几何直观的依赖程度,在组织单元教学时更需要把握这一点.上述使用的“一题多解”、“一题多变”及“多题一解”等变式手段,本质上都是服务于“数形结合”这一思想方法,是提高学生发散思维与形象思维的有效途径. 核心素养统领下的数学教育注重数学的整体性、思想的一致性、逻辑的连贯性和思维的系统性[6],单元教学设计的初衷正在于此.今后,怎样融入变式元素以更好地体现“数学的方式”,如何规划变式设计更有利于把握“数学的本质”,还需要我们在教学实践中不断求索.3 整合单元知识,升华变式思维
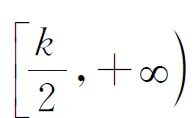


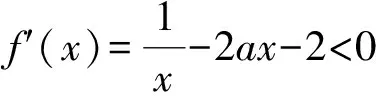
4 贯穿单元体系,把握变式本质