成语与寓言中的概率思维

欧阳顺湘

(哈尔滨工业大学(深圳) 518055)

英国经济学家、政治社会学家白哲特(Walter Bagehot，1826-1877)曾说“生活是概率的大学校”. 法国数学家拉普拉斯在其《分析概率论》有句常被引用的名言：“生活中最重要的问题，绝大部分其实只是概率问题.”Leo Breiman在其概率论著作[1]的序言写道：“概率论有两手，右手是严格地使用测度论的基础工作，左手是‘概率地思考’，将问题变成赌博，投骰子，粒子运动问题.”另一方面，不少成语、寓言是生活智慧的结晶. 所以，很自然地，一些成语和寓言蕴含着概率思维. 我们可以通过成语与寓言来直观地了解一些概率思想，也可以用概率思维来更好地理解一些成语与故事. 我们下面就按概率论中讨论的一些内容分类介绍相关成语.

1 随机现象与随机事件

“天有不测风云”反映了人们对随机现象无处不在的认识.“守株待兔”故事中的农夫错在将随机现象将当成确定性现象，或说错在高估了兔子撞树桩这个随机事件发生的概率.“水中捞月”则是将不可能事件当作了可能事件. 还有些成语说明随机事件发生可能性大小，如“稳操胜券”“十拿九稳”“百发百中”等.

“万事皆有因”“有果必有因”则反映了人们对包括随机现象在内的各种现象产生的原因的探究. 如一些人曾认为人的命运由生辰八字决定，认为一些结果是“命中注定”. 在婚配等问题上要研究是否“八字不合”. 实际上，人的生辰充满随机性，所有八字组合也只有有限种可能结果，远远不能决定丰富多彩的人生.

很多人认为随机现象源于无知：古希腊哲学家德谟克利特认为“一切都遵照必然而产生”，牛顿、拉普拉斯等提倡决定论，爱因斯坦也认为“上帝不掷骰子”. 现在，一般认为量子力学中出现的随机现象是真正的随机.

随机现象的出现并不是坏事. 例如，许多人设定密码时常利用手机号、生日、或门牌号等. 密码破译者可能会利用这个偏好来猜测密码. 如果是随机生成的密码，就很难猜测了.又如，在剪刀-石头-布游戏中，有的高手能计算出对方出招的模式，预测出对方的下一手.为与高手对抗，可以考虑随机策略，即随机出剪刀、石头或布，这样可以达到纳什均衡. 类似地，生物学中基因突变与重组的随机性使得生物呈现出多样性，从而保证了各种子代的产生以适应自然选择. 这三者的策略可谓“随机应变”——如果允许我们将它“曲解”为用“随机”的办法来对抗. “狡兔三窟”，也同样是利用了随机性来提高安全性，其做法异曲同工.

2 小概率事件

设某随机事件A发生的概率为p>0，则它不发生的概率为1-p，在n次独立重复试验中，A不发生的概率为(1-p)n. 当n趋于无穷时，A发生的概率1-(1-p)n趋于1.

由此可知，一个随机事件单次发生的概率虽然可能很小，但在充分多次独立重复试验中，它至少发生一次的概率将很大. 这就导致所谓的墨菲定律：一件事情发生的概率无论有多小，只要有可能发生，就几乎一定会发生. 它可以解释很多现象：为什么自然界中会出现一些巧夺天工的奇迹？为什么参加高考如此重要的事情，总有新闻报道说有学生临到考场才发现忘带准考证.

不少成语体现了小概率事件的作用([2]对部分此类成语做了一些讨论). 如有的成语总结人多力量大：“三人行，必有我师焉”“三个臭皮匠，顶个诸葛亮”“一根筷子容易折，一把筷子难折断”；有的成语劝人坚持不懈：“水滴石穿”“锲而不舍，金石可镂”“只要功夫深，铁杵磨成针”. 有的成语对人发出警戒，劝人谨慎：“常在河边走，哪有不湿鞋”“不怕一万，就怕万一”“勿以善小而不为，勿以恶小而为之”“千里之堤，溃于蚁穴”.

法国数学家波莱尔在1909年出版的一本谈概率的书籍中介绍了“打字的猴子”，设想猴子随机敲击键盘. 于是就有了所谓的无限猴子定理：设有无限只猴子，且允许使用无限的时间，则一定会有一只猴子打出所要求的书籍或文章. 如打出大英图书馆的全部著作，或莎士比亚的著作等等. 但这里需要允许使用任意长的时间. 农夫“守株待兔”并非不可能事件，只要等待足够长时间，也可以期望再次不劳而获. 但农夫不事劳作，仅仅期待这个小概率事件多次发生以供生活所需，需要极大的耐心和时间成本，得不偿失.

3 大数定律

大数定律说一事件在多次独立重复试验中发生的频率稳定于该事件发生的概率. 例如，投掷一枚均匀的硬币多次，其中正面朝上的次数大约为一半. 这与成语“万变不离其宗”有类似处.

在生活中，人们常会咨询多位朋友或专家的意见再做决策，其目的就是通过听取各种意见，综合考虑，尽力消除随机因素的影响. 这就是“集思广益”有作用的原理. 其思想与大数定律一样.

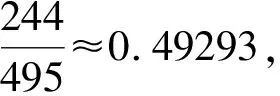
伊索寓言“龟兔赛跑”讲兔子因为在比赛中睡大觉而输的故事. 常见解读是兔子不够稳重不值得学习，乌龟勤恳堪称模范. 罗森塔尔认为这是对随机性的漠视[3]. 他建议用概率视角准确理解这个故事. 按照大数定律，赛跑的关键不在于谁更可靠、谁更稳重，而在于谁的平均速度更快. 长远来看，谁平均跑得快，谁在比赛中就一定能赢.

4 Poisson聚集

生活中不乏见到“屋漏偏遭连夜雨”这样接二连三倒霉的事情，也可能遇到“双喜临门”这样好运不断的好事. 如某地突然连续出现多起刑事案件，又如近期与一个平常难得一见的朋友多次偶遇. 这样的巧合为什么并不乏见？随机地发生的事情，为什么会“碰巧”聚集在一起？“无巧不成书”的背后其实也有概率解释. 数学上，人们称之为Poisson聚集(Poisson Clumping). 下面的例子可以说明这种现象.

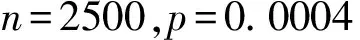
我们可以用参数λ=np=1为Poisson分布近似这个二项分布，即对任意k=0,1,2,…,n，

由此可得在一个小正方形区域中有不少于5个落点的概率约为0.004. 因此，平均而言，每250个小正方形区域中就有1个小区域中的落点数不少于5. 在上述随机落点中，平均有10个小区域中的落点数不少于5. 所以，在一些小区域中有点的聚集并不是意外.

在第二次世界大战中，伦敦受到德军飞弹的打击，一些地区似乎更常被打击. 英国统计学家R.D. Clark用类似于上述例子中的方法，推断出德军的袭击是随机的.

5 贝叶斯定理

贝叶斯学派认为概率是人们对某件事情发生可能性大小的主观判断，随着所知信息的改变而改变，即所有的概率都是条件概率. 信息可以消除不确定性.

《韩非子》中的寓言故事“智子疑邻”以及《列子》中的寓言故事“疑邻盗斧”说的是人们的主观判断受到一些因素的影响. 对这两个故事的常见解释是“应该实事求是,尊重客观事实,不要主观臆断”. 事实上，虽然无根据的“臆断”要尽量避免，但主观判断无处不在. 概率的频率解释要求试验可多次重复，但有很多事件是难以重复的，如某地发生地震，其发生的概率就没法用频率解释，只能用主观判断.

贝叶斯提出的贝叶斯定理可以帮助人们推理.下面是贝叶斯定理的简单版本.

设事件A或Ac导致事件B发生，且A,Ac发生的概率P(A),P(Ac)已知，不为零，在A或Ac发生的条件下B发生的概率P(B|A),P(B|Ac)也已知. 如果事件B发生了，概率不为零，我们可以用贝叶斯公式确定A发生的概率

其中B发生的概率可以全概率公式计算如下

P(B)=P(B∩A)+P(B∩Ac)

=P(B|A)P(A)+P(B|Ac)P(Ac).

我们称P(A)为A的先验概率，在B发生后，A发生的概率更新为P(A|B)，称之为A的后验概率. 如果还有别的信息，我们可以将P(A|B)当作A发生的先验概率，重复上述过程再次更新我们对A发生的概率的认识.

《战国策》中记载有寓言故事“三人成虎”：

庞葱与太子质于邯郸，谓魏王曰：“今一人言市有虎，王信之乎？”王曰：“否.”“二人言市有虎，王信之乎？”王曰：“寡人疑之矣.”“三人言市有虎，王信之乎？”王曰：“寡人信之矣.”庞葱曰：“夫市之无虎明矣，然而三人言而成虎.今邯郸去大梁也远于市，而议臣者过于三人，愿王察之.”王曰：“寡人自为知.”于是辞行，而谗言先至.后太子罢质，果不得见.

这个故事生动地刻画了魏王不断修正自己对“市有虎”这件事发生的概率的大小的过程. 我们用贝叶斯定理量化说明这个过程如下:

用T表示“市有虎”这件事. 一般而言，闹市难得有虎，可假设有虎的先验概率较小，为0.03，即

P(T)=0.03,P(Tc)=0.97.

用R1,R2,R3分别表示第一、二、三人向魏王报告市有虎. 设三人的行为独立且相同，在市有虎的条件下，报告有虎的概率为0.7，没虎却有意生谣或看错了(如把玩具虎当作真虎)的概率为0.1，即对i=1,2,3,有

P(Ri|T)=0.7,P(Ri|Tc)=0.1.

由贝叶斯公式，一人言市有虎的条件下，魏王相信市有虎的概率被修正为：

这个概率比先验概率稍微有所增加；但不足以使魏王相信，所以魏王说“否”. 现在第二人言市有虎，我们把有虎的后验概率P(T|R1)≈0.178当作T的先验概率，重复前面的计算，可得后验概率

这个概率也不大不小，所以魏王“疑之”. 再次重复，可得在第三人言市有虎的条件下，魏王认为市有虎的后验概率为

P(T|R3)≈0.914.

至此，魏王“信之矣”.

《战国策》中记载“曾参杀人”与“三人成虎”类似. 伊索寓言“狼来了”，也是一个不断修订概率的过程. 但“狼来了”与“三人成虎”“曾参杀人”有所区别(1)《贝叶斯版的“三人成虎”》(王志祥，宋 涛，数学文化，8(4):111-112, 2017；或同作者所著《数学杂谈》，天津大学出版社，2017)一文用贝叶斯公式讨论了三人成虎. 我们认为该文的逻辑适合于分析“狼来了”，不适合于分析“三人成虎”. 请读者留意.. 一是三人依次欺骗同一人(魏王、曾母)；一是同一人(放羊娃)三次欺骗同一批农夫.

从“三人成虎”等故事可见“众口铄金”的危害, 需要警惕谣言. 奉行“事不过三”准则的人也要警惕，明辨是非. 在现代信息交流便利的情况下，网络谣言盛行，其原因可以用贝叶斯推理解释，但我们也可以用贝叶斯推理来帮助我们甄别谣言. 其应用原理与上述三人成虎的概率推理类似. 垃圾邮件过滤，语音识别，拼写检测，搜索引擎和输入法智能纠误等都与此类似.

6 结语

我们从概率视角解释了“水滴石穿”“集思广益”“无巧不成书”等成语以及“狡兔三窟”“龟兔赛跑”“疑邻盗斧”“三人成虎”等寓言故事. 这样做，一方面可以使人们对一些成语与寓言故事有新的认识，了解到其中所蕴含的概率智慧. 另一方面，通过人们熟知的成语和寓言故事来阐述概率思维可以激发学习者的学习兴趣，加深学习者对概率的理解.