Gorenstein dimensions for weak Hopf-Galois extensions

(School of Mathematics, Southeast University, Nanjing 211189, China)(School of Science, Jinling Institute of Technology, Nanjing 211169, China)

Abstract：The representation of weak Hopf algebras is studied by investigating the Gorenstein dimensions of weak Hopf algebras and weak Hopf-Galois extensions. Let H be a weak Hopf algebra with a bijective antipode, A a weak right H-comodule algebra and B the H-coinvariant subalgebra of A. First, some properties of Gorenstein projective H-modules in the representation category are studied, and the fact that Gorenstein global dimension of H is the same as the Gorenstein projective dimension of its left unital subalgebra is demonstrated. Secondly, by applying the integral theory of weak Hopf algebras, on the one hand, a sufficient and necessary condition that a projective A-module is a projective B-module is given; on the other hand, the separability of the functor A⊗B- and that of the restriction of scalar function B(-) are described, respectively. Finally, as a mean result, the Gorenstein global dimension of a weak Hopf-Galois extension is investigated under the condition that H is both semisimple and cosemisimple.

Key words：weak Hopf algebra; integral; weak Hopf-Galois extension; Gorenstein dimension

The study of Gorenstein projective modules can be traced back to Ref.[1], where theG-dimension of a finitely generated module over a two-sided Noetherian ring was introduced. Furthermore, the definition of Gorenstein projective modules was given in Ref.[2]. We knew already that a module ofG-dimension zero is actually a Gorenstein projective module. Gorenstein projective modules play an important role in many areas. For example, they are widely used in the representation theory of Artin algebras, the theory of stable and singularity categories, and the cohomology theory of commutative rings, and so on.

Weak bialgebras and weak Hopf algebras introduced in Ref.[3] generalized the ordinary bialgebras and Hopf algebras by weakening the comultiplication of unit and the multiplication of counit. Comultiplication is allowed to be non-unital, but it is still coassociative. In exchange for coassociativity, the multiplicativity of the counit is replaced by a weaker condition, implying that the unit representation is not necessarily one-dimensional and irreducible. Weak Hopf algebras can provide us with a good framework for studying the symmetries of certain quantum field theories. Groupoid algebras, face algebras and generalized Kac algebras are examples of weak Hopf algebras.

The main purpose of this paper is to study the representation of weak Hopf algebras by investigating the Gorenstein dimensions of weak Hopf algebras and weak Hopf-Galois extensions. LetHbe a weak Hopf algebra with a bijective antipode,Aa weak rightH-comodule algebra andBtheH-coinvariant subalgebra ofA. After recalling some basic definitions and giving a summary of the fundamental properties concerned with weak Hopf algebras, we study some properties of Gorenstein projectiveH-modules in representation category, and find that the Gorenstein global dimension ofHis the same as the Gorenstein projective dimension of its left unital subalgebra. By applying the integral theory of weak Hopf algebras, on the one hand, we give a sufficient and necessary condition that a projectiveA-module is a projectiveB-module; on the other hand, we describe the separability of the functorA⊗B- and that of the restriction of scalar functionB(-). Consequently, we investigate the Gorenstein global dimension of a weak Hopf-Galois extension.

1 Preliminaries

Throughout this article,kdenotes a fixed field, and we will always work overk. The tensor product ⊗:=⊗kand Hom-functor are always assumed to be overk. We also use Sweedler’s notations for the terminologies on coalgebras and comodules. For a coalgebraC, we write the comultiplicationΔ(c)=∑c1⊗c2for anyc∈C. For a rightC-comoduleM, we denote its coaction byρ(m)=∑m(0)⊗m(1)for anym∈M. For any unexplained definitions and notations, one may refer to Ref.[4] or Ref.[5].

Definition1[3]A weak Hopf algebraHis an algebra (H,μ,η) and a coalgebra (H,Δ,ε) such that

Δ(xy)=Δ(x)Δ(y)

(1)

ε(xyz)=∑ε(xy1)ε(y2z)=∑ε(xy2)ε(y1z) (2)

Δ2(1H)=(Δ(1H)⊗1H)(1H⊗Δ(1H))=

(1H⊗Δ(1H))(Δ(1H)⊗1H)

(3)

and there exists a linear mapS:H→H, called an antipode, satisfying

(4)

LetHbe a weak Hopf algebra. The imagesHt=εt(h) andHs=εs(h) of the projectionsεt,εs:H→Hdefined by

εt(h)=∑ε(11h)12,εs(h)=∑11ε(h12)

are both separable subalgebras ofHand commute with each other[3].HtandHsare called left and right unital subalgebras, respectively.

Definition2[3]A left integral inHis an element l∈Hsatisfyinghl=εt(h)lfor allh∈H. Furthermore, ifεt(l)=1H, then it is said to be normalized. A normalized right integral is defined similarly. A left or right integral inHis called non-degenerate if it defines a non-degenerate functional onH*, the dual space ofH.

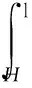
∑S(hl1)⊗l2=∑l1⊗hl2

(5)

∑h1λ(gh2)=∑λ(g2h)S(g1)

(6)

∑λ(S-1(l)h)=ε(h)

(7)

LetHbe a weak Hopf algebra with an antipodeS. According to Refs.[8-9], we have

(8)

(9)

(10)

(11)

Definition3[10]LetHbe a weak Hopf algebra, andAa rightH-comodule, which is also an associative algebra. We callAa weak rightH-comodule algebra if

ρ(ab)=ρ(a)ρ(b)

(12)

∑a1(0)⊗1(1)=∑a(0)⊗εt(a(1))

(13)

for alla,b∈A.

LetHbe a weak Hopf algebra, andAa weak rightH-comodule algebra. Then, according to Ref.[8], we obtain that

∑a1(0)⊗εs(1(1))

(14)

Define theH-coinvariant subalgebra ofAas

Then, we know from Ref.[11] that

Definition4[12]LetAbe a weak rightH-comodule algebra andBtheH-coinvariant subalgebra ofA. The extensionA/Bis said to be weak Hopf-Galois, if the canonical map

β:A⊗BA→A⊗sH,β(a⊗Bb)=∑ab(0)⊗sb(1)

2 Gorenstein Global Dimensions for Weak Hopf Algebras

For a ringR, we denote the class of projective leftR-modules by P, and for an objectMinRM, the category of leftR-modules, we denote the projective and injective dimension ofMbyp.dimRMandi.dimRM, respectively.

Definition5[13]A leftR-moduleMis Gorenstein projective if there exists anRHom(-,P)-exact sequence

…→P1→P0→P0→P1→…

such thatM=Ker(P0→P1), where everyPiandPiare projective.

Dually, Gorenstein injective leftR-modules can be defined.

Definition6For a leftR-moduleM, the Gorenstein projective dimension G.p.dimRMis at mostnif there is an exact sequence

0→Gn→Gn-1→…→G1→G0→M→0

where everyGiis Gorenstein projective.

Dually, the Gorenstein injective dimension G.i.dimRMcan be defined.

For any ringR, Ref.[14] shows us that

sup{G.p.dimRM|M∈RM}=sup{G.i.dimRM|M∈RM}

The common value is called the left Gorenstein global dimension ofRand denoted as G.gl.dim(R).

We know that G.gl.dim(R)=0 if and only if the ringRis quasi-Frobenius[15]. In addition,Ris left Gorenstein hereditary if every submodule of a projective leftR-module is Gorenstein projective[16], i.e., G.gl.dim(R)≤1.

In what follows, we always assume thatHis a weak Hopf algebra with a bijective antipodeS. Then, the leftH-module categoryHM, called the representation category, is an abelian monoidal category[17-18]such that

•Htis the unit object with a leftH-action viah·x=εt(hx) for allh∈Handx∈Ht;

• ForM,N∈HM, the tensor product isM⊗tN:=M⊗HtN, where the rightHt-module structure onMis defined bym·x=S-1(x)·mfor allm∈Mandx∈Ht;

• The leftH-module structure onM⊗tNis defined by the following diagnosing actionh·(m⊗tn)=h1·m⊗th2·n, for allh∈H,m∈M,n∈N;

• ForM,N∈HM, a homomorphism betweenMandNis leftH-linear.

Proposition1IfPis a Gorenstein projective leftH-module, then so isP⊗tXfor any leftH-moduleX.

ProofIfPis a Gorenstein projective leftH-module, then there is anHHom(-,P)-exact sequence

P:…→P1→P0→P0→P1→…

such thatM=Ker(P0→P1), where everyPiandPiare projective. AsHtis separable, we can obtain an exact sequence

P⊗tX:…→P⊗tX→P0⊗tX→P0⊗tX→P1⊗tX→…

such thatM⊗tX=Ker(P0⊗tX→P1⊗tX). Meanwhile, everyPi⊗tXandPi⊗tXare projective leftH-modules[19]. For any projective leftH-moduleQ,

HHom(P⊗tX,Q)≅HtHom(X,HHom(P,Q))

Hence,HHom(P⊗tX,Q) is exact, as desired.

Theorem1LetHbe a weak Hopf algebra with a bijective antipodeS. Then, G.gl.dim(H)=G.p.dimHHt.

ProofObviously, G.gl.dim(H)≥G.p.dimHHt. Hence, we shall prove the reverse inequality. Assume that G.p.dimHHt=n<+∞. Then, there is an exact sequence

0→Gn→Gn-1→…→G1→G0→Ht→0

where everyGiis Gorenstein projective. For any leftH-moduleX, we obtain an exact sequence

0→Gn⊗tX→Gn-1⊗tX→…→G1⊗tX→

G0⊗tX→Ht⊗tX→0

AsHt⊗tX≅X, and everyGi⊗tXis Gorenstein projective by Proposition 1, we obtain G.gl.dim(H)≤n. This shows that G.gl.dim(H)≤G.p.dimHHt.

3 Gorenstein Global Dimensions for Weak Hopf-Galois Extensions

β-1(1A⊗sh)=∑ili(h)⊗Bri(h)∈A⊗BA

such that

∑∑ili(h)ri(h)(0)⊗sri(h)(1)=1A⊗sh(15)

by definition. Such elements enjoy the following properties.

Lemma1[20]For alla∈Aandh∈H, we have

∑ili(h)ri(h)=∑ε(h1(1))1(0)

∑∑ili(h)⊗Bri(h)(0)⊗sri(h)(1)=

∑∑ili(h1)⊗Bri(h1)⊗sh2

∑∑ili(h)(0)⊗Bri(h)⊗sli(h)(1)=

∑∑ili(h2)⊗Bri(h2)⊗sS(h1)

Consider the two functors:

A⊗B-:BM→AM,NA⊗BN

B(-):AM→BM,MBM

whereB(-) is the restriction of the scalars functor.

Lemma2(A⊗B-,B(-)) and (B(-),A⊗B-) are double adjunctions.

ProofNote that the element ∑λ(a(1))a(0)∈B[21]fora∈A. Then, for allN∈BM, we have a well-defined mapφ:A⊗BN→BHom(A,N) given by

φ(a⊗Bn)(b)=∑λ(b(1)a(1))b(1)a(0)·n

a,b∈A,n∈N

Then, it is easy to check thatφis a morphism of leftA-modules, whereBHom(A,N)∈AMvia (a·f)(b)=f(ba) for alla,b∈Aandf∈BHom(A,N). Meanwhile, we claim thatφis a bijection with the inverse given by

φ:BHom(A,N)→A⊗BN

φ(f)=∑li(S-1(l ))⊗Bf(ri(S-1(l )))

Indeed, on the one hand, for alla,b∈Aandn∈N, by Lemma 1, we have

φφ(a⊗Bn)=

∑∑ili(S-1(l ))⊗Bλ(ri(S-1a(1))ri(S-1a(0)·n=

∑∑ili(S-1(l ))ri(S-1a(0)λ(ri(S-1a(1))⊗Bn=

∑∑ili(S-1(l2))ri(S-1(12))a(0)λ(S-1(l1)a(1))⊗Bn=

∑1(0)a(0)λ(S-1(l )1(1)a(1))⊗Bn

On the other hand, for allb∈Aandf∈BHom(A,N), by Lemma 1, we have

φφ(f)(b)=

∑∑iλ(b(1)li(S-1(l ))(1))b(0)li(S-1(l ))(0)·

f(ri(S-1(l )))n=

∑∑iλ(b(1)l2)f(b(0)li(S-1(l1))ri(S-1(l1)))=

∑λ(l2)ε(S-1(l1)b(1)1(1))f(b(0)1(0))=

∑λ(l2)ε(S-1(l1)b(1))f(b(0))n=f(b)

Hence, the adjoint isomorphism theorem, (A⊗B-,B(-)) and (B(-),A⊗B-) are double adjunctions[12].

By Lemma 2, we have the following assertion.

Corollary1IfP∈BMis projective, thenA⊗BP∈AMis projective.

Lemma3IfHis semisimple andP∈AM, thenPis projective as a leftA-module if and only ifPis projective as a leftB-module.

∑iali(J)⊗Bri(J)=∑ili(J)⊗Bri(J)a

(16)

In fact, by Lemma 1, we have

∑∑iali(J)ri(J)(0)⊗sri(J)(1)=

∑∑iali(J1)ri(J1)⊗s2J2=

as needed.

for allp∈P.

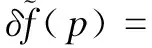
∑ili(J)ri(J)·ξ(p)=∑ε(J1(1))1(0)·ξ(p)=

∑ε(εs(J)1(1))1(0)·ξ(p)=∑ε(1(1))1(0)·ξ(p)=

1A·ξ(p)=ξ(p)

Conversely, suppose thatPis projective as a leftA-module. It follows from Lemma 2 that (A⊗B-,B(-)) is an adjoint pair. SinceAis projective as a rightB-module[22], we obtain that the functorA⊗B- is exact. Hence,B(-) preserves projective objects. Therefore,Pis projective asB-module.

Lemma41) IfHis semisimple, thenB(-) is separable.

2) IfH*is semisimple, thenA⊗B- is separable.

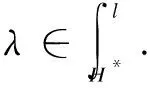
Corollary21) IfHis semisimple, thenMis a left A-module direct summand ofA⊗BMfor allM∈AM.

2) IfH*is semisimple, thenNis a leftB-module direct summand ofA⊗BNfor allN∈BM.

Proof1) AsHis semisimple, we know from Lemma 4 thatB(-) is separable. Hence, the counit:of the adjunction (A⊗B-,B(-)) is a cosplit epimorphism[11], that is, there is a natural transformationfor allM∈AM. Thus,Mis a leftA-module direct summand ofA⊗BM.

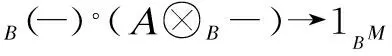
Lemma5IfN∈BMis Gorenstein projective, thenA⊗BN∈AMis Gorenstein projective.

ProofSuppose thatNis a Gorenstein projective leftB-module. Then, there is aBHom(-,P)-exact sequence

P:…→P1→P0→P0→P1→…

such thatN=Ker(P0→P1), where everyPiandPiare projective. SinceAis projective as a rightB-module, we obtain thatA⊗BPis exact andA⊗BN=Ker(A⊗BP0→A⊗BP1). We also obtain thatA⊗BPiis projective for everyibecause of the assertion thatB(-) is exact andA⊗B- is a left adjoint[12].

Let us suppose finally thatQ∈AMis Gorenstein projective. Then,

AHom(A⊗BP,Q)≅BHom(P,Q)

However,BQis projective sinceB(-) is a left adjoint ofA⊗B- which is exact. Thus,BHom(P,Q) is exact sinceNis Gorenstein projective, and so,AHom(A⊗BP,Q) is also exact, which implies thatA⊗BNis Gorenstein projective.

Theorem2IfHis a semisimple and cosemisimple weak Hopf algebra, then G.gl.dim(A)=G.gl.dimB.

ProofAssume that G.gl.dimB=n<+∞. For anyM∈AM, as a leftB-module, there is a Gorenstein projective resolution:

0→Gn→Gn-1→…→G1→G0→M→0

where everyGiis Gorenstein projective. Since the functorA⊗B- is exact, it induces a leftA-module exact sequence

0→A⊗BGn→A⊗BGn-1→…→

A⊗BG1→A⊗BG0→A⊗BM→0

From Lemma 5, we know that everyA⊗BGiis Gorenstein projective, and thus, G.gl.dimA(A⊗BM)≤n. SinceMis a direct summand ofA⊗BMas leftA-modules by Corollary 2, G.gl.dimAM≤n[26]. Hence, G.gl.dim(A)≤n.

Suppose that G.gl.dim(A)=q≤n=G.gl.dimB. Then, G.gl.dimB(A⊗BN)≤qfor anyN∈BM. Therefore,BExti(A⊗BN,U)=0 for alli>qand all projective leftB-moduleU[26]. SinceNis a leftB-module direct summand ofA⊗BNand the functorBExt(-,U) preserves finite direct sums,BExt(N,U)=0 for alli>qand all projective leftB-moduleU, and, hence, G.gl.dimBN≤q. This implies that G.gl.dim(A)≤G.gl.dimB. Therefore, in view of the above discussion, we have G.gl.dim(A)=G.gl.dimB.

Corollary3LetHbe a semisimple and cosemisimple weak Hopf algebra. Then,Ais quasi-Frobenius (rep. left Gorenstein hereditary) if and only if so isB.

In particular, ifR#His a weak smash product of a weak leftH-module algebraR(see Ref.[24] for the definitions), thenR#His quasi-Frobenius (rep. left Gorenstein hereditary) if and only if so isR.