核心素养背景下高中数学教师的价值追求

成 梁

（上海市华东模范中学 上海 200040）

从上世纪60年代以来，数学教学目标经历了如下演变：“三大能力”，“素质教育”，“三维目标”，“四基”，“核心素养”。

数学核心素养包含数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析等六个方面。提倡“核心素养”，要求我们为发展学生的核心素养而教：以发展学生核心素养为目标指向，以数学知识为载体，以数学概念的内在逻辑为线索，精心选择学习素材，构建学习情境，设计符合学生认知规律的、自然而目标明确的系列数学活动，引导学生通过多样化的学习方式，掌握数学双基，形成思维能力，并在运用数学知识解决问题的过程中培养创新精神和实践能力，从而实现核心素养的发展目标。

数学教育的终极目标是：使学生会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。数学学科教学活动是数学学科核心素养培养的主要途径，也是数学教师价值追求的重要手段。那么，数学教学到底教什么呢？根据数学核心素养的要求，可以很自然地得出：数学教学应该教理解、教思维、教思想方法。

1 教理解

教师在教学时通常出现下列错误倾向：快速教学相关概念、原理等新知内容后就进行大量机械重复训练或题型归类训练。但是，如果不是真正理解，碰到没见过的题，学生往往就会束手无策。

案例1：二项式定理的学习过程中，快速教学相关概念、原理，课本上一些基础的练习可能还能处理。但若问展开式一共有多少项？含有项的系数是多少？实际教学中对二项式定理理解不够深刻就有无从下手的感觉。在教学中，老师应该引导启发学生理解二项式定理本质，理解二项式定理是排列和组合的运用，二项式定理中项数为什么是项，每一项的系数有何规律，二项式定理又是如何推出的，而不是仅仅背几个结论。教学需要揭示数学本质：变“单薄”为“厚重”。

只有理解公式定理的来龙去脉，理解公式定理的本质，才能避免“题海战”。

2 教思维

2.1 概念教学渗透思维

在概念教学中，教师往往先展示一个似与概念相关的情景（有时此环节省略），再照本宣科地抛出概念，或学生看教科书中概念的表述，然后教师提出该概念的注意事项，最后是理解概念的相关练习，比如通过关键字、词设计的填空题，正例反例判断题，简单的应用等。

这种被老师牵引的仅围绕概念“是什么”展开的教学，学生的思维参与及情感投入都是低水平的，很难和概念形成亲密关系，对概念的理解是肤浅的就会在所难免。因此老师要设计体现概念本质的一些问题，以帮助学生理解概念的内涵与外延。

案例3：函数奇偶性的概念。

要理解奇函数的概念，最重要的要理解概念中任意这两个字，设计这样几个例题是必须的：

2.2 变式训练拓展思维

变式练习可以训练他们的类比、归纳、联想等一些命题变化的基本技能，甚至可以在变化的过程中发现一些有趣的数学问题，既提高了学生学习数学的兴趣，也使他们认清一些数学问题的来龙去脉，从而提高问题解决的参与感，为数学教师提供源源不断的数学问题研究素材。

例如在函数单调性的概念教学中，函数的单调性是学生进入高中后较早接触的一个完全形式化的抽象定义，对于仍然处于具体形象思维阶段的高一学生来说，有较大的学习困难。教师在教学问题的设计上要重视变式训练。

以上命题正确的选项是：

A．①③ B．②③ C．②④ D．②

在变式训练中，要让学生成为变式训练的主体：

（1）要让学生进行“要我变”的训练。

（2）在学生“要我变”的基础上，让学生主动地产生“我要变”的欲望。例如在一张试卷的最后可以采取开放式加试题：请你针对本卷中的任何一个问题进行变式，使之成为一个有趣的或者比较有意义的数学问题，并给出你的解答或发现、建议等。

（3）对学生进行一些数学问题变化技能的训练（“如何变”）。例如可以利用四种数学命题之间的变化进行变题训练；可以利用类比、归纳、实验、猜想等数学思想方法创设一种让学生产生数学问题变化欲望的情境。

2.3 一题多解活跃思维

对于一些经典问题，教师要注意引导学生一题多解，激发学生兴趣，这样学生就会思维活跃，思路开阔，

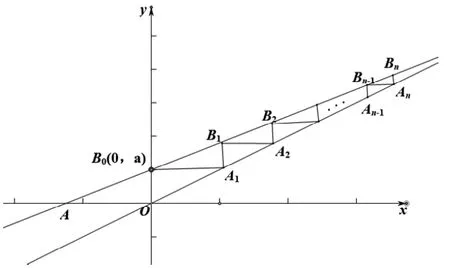
这个问题可以采用待定系数法、累加法、还可以根据递推关系得到再求和即可。在对等比数列求和。这些方法在解决求数列通项公式的时候都很常用，具有很好的启发作用。

3 教思想方法

高中常见的数学思想方法有：数形结合（抽象与直观）、函数与方程（动与静、等与不等）、分类讨论、化归思想（转化与归结）。高中数学中解题的本质是化生为熟、化难为易、化繁为简、化杂为单、化抽象为直观、化一般为特殊、化不等为等、化动态为静态、化乱为谐。在解题中常用的工具性知识有坐标系、向量、基本量等。解题中常用的方法主要有消元、换元等。转化思想是数学学习过程中常用的思想方法，是数学问题解决的基本思路和途径之一。传颂千古的司马光砸缸、曹冲称象等故事，都成功地运用了转化的策略。

将空间问题转化为平面解决，将长方体表面展开，在平面内解决，两点之间线段最短。

数学核心素养是学生在学习过程中，形成的适应个人终身发展和社会发展需要的数学思维品质与关键能力以及相关的情感、态度与价值观。要求教师在数学教学活动中，更多地关注学生的思维过程，抓住数学的本质，创设合适的教学情境、提出合适的问题，启发学生独立思考或与他人进行有价值的讨论，让学生在掌握知识技能的同时，感悟数学的思想，积累数学思维的经验，形成和发展数学核心素养。这一切也恰恰形成了高中数学教师的价值追求。