四旋翼飞行器软件设计*
2021-01-12马亨杰王硕之
马亨杰,王硕之
(1.闽江学院计算机与控制工程学院,福建 福州 350108;2.厦门理工学院电气工程与自动化学院,福建 厦门 361012)
1 引言
1907年,在Charles Richet教授的帮助下,Breguet兄弟进行了第一次旋翼机的设计尝试,并设计出“Gyroplane No.I”(旋翼机一号)。“旋翼机一号”的机身由钢管搭接构成,中心配备一个供驾驶员使用的座椅和部分动力装置,四个钢索支撑的钢管臂从中间向四个方向延伸,每个支撑臂末端都有一对同轴相叠的四叶片转子。两个转子组顺时针旋转,两个逆时针旋转。同时,为了克服扭矩效应,相同旋转方向的转子组间隔安装在支撑臂末端[1]。
从近年的发展趋势来看,四旋翼飞行器渐渐由体积庞大的钢架结构转向轻便、迷你结构,越来越多的工程作业会考虑加入四旋翼飞行器进行辅助勘测。同时,为满足工程所需要的作业能力,通过对通讯技术、开发环境、可操作性等诸多方面的研究探索,技术人员提高了四旋翼飞行器的稳定性、灵敏度等性能[2]。
为了进一步提高飞行器的稳定性、灵敏度,本文采用了卡尔曼滤波和PID算法。卡尔曼滤波的测量结果随时间变化,包含统计噪声和其他不定杂波,并产生未知变量的估计值,而PID算法是一种较为常用的自动控制算法。本文中,控制模块的前期姿态融合算法采用卡尔曼滤波,后期算法则采用PID算法来做最终的姿态控制[3]。并在最后对该算法进行了实验与测试。
2 四旋翼飞行器软件设计
2.1 卡尔曼滤波
卡尔曼滤波是一种算法滤波,它的测量结果随时间变化,包含统计噪声和其他不定杂波,并产生未知变量的估计值[4]。这些估计值基于通过估计每个时间范围内变量的联合概率分布,单独进行单一测量。卡尔曼滤波器可以写成单个方程,但它通常按照概念不同,分为2个不同的阶段:“预测”和“更新”。预测阶段使用来自之前时间单元的状态来估计当前时间单元的状态,在更新阶段,当前的先验预测与当前的观测信息相结合以改进状态估计,这个改进的估计被称为后验状态估计。
本文选用卡尔曼滤波算法(图1),是因为在实际情况下我们无法直接获得飞行器的准确姿态,而利用卡尔曼算法可以算出四轴当前的准确姿态,从而达到提升飞行器飞行的平稳程度及灵敏程度,更便于地面控制者的操作,达到灵敏、稳定的效果。 涉及卡尔曼滤波算法,先要讨论基准点的确立。陀螺仪得到±250范围的数据来表示转动角速度。需要额外注意的是,±250的数据需要将原始数据减去基准点数据之后得到的。
上文提及的基准点指的是传感器处于零负荷时候的输出数据。例如反应的Rol、Pit、Yaw三个方向的转动角速度,如果陀螺仪没有转动,则输出为0。但是在实际情况下,考虑环境干扰等因素,通常会有初始值。因此需要进行标零,即在四旋翼飞行器起飞前水平放置进行标零,确立水平面。初始化完成之后,将得到的姿态传感器数据输入到相应的姿态解算算法中,以便于计算四轴的准确姿态。
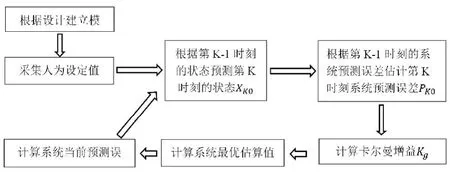
图1 卡尔曼滤波算法流程图
下面以横滚方向姿态变量Reading_IntegralGyroRoll为例,分析在这种算法中数据的产生和处理过程。 第1步:存储采集数据与放大加速度计采集的数据。将采集到的数据进行正反向设置和减去中立点操作,并重新用新的变量名为上述数据进行存储。这样做的优点在于新的数据仍旧可以被存储在原本的变量名中,且对新的变量名进行处理之后可以方便清除已经使用过的数据,从而达到存储空间的相对优化利用。
第2步:将陀螺仪和加速度计的数据都进行积分处理。并且与后面的长期融合计算得出的误差修正量进行校正补偿。进行了初步积分计算处理之后,设定一个变量balance_number为对初步积分计算的结果的采样次数,并且进行多次采样。当采样次数超过2^8(256)次之后,进行长期融合处理,即:将所得数据设定修正为长期数据。
第3步:对于陀螺仪数据的积分结果再次进行积分。
第4步:短期数据融合。用加速度传感器采集的瞬时数值乘以系数,来修正陀螺仪采集数据的积分。接着输入PID调节器中,控制电机依据合适的功率转动。
第5步:长期数据融合。当短期融合次数达到了所定义的次数,接着执行长期融合。设定一个长期融合后得到的变量AttitudeCorrectionRoll。长期融合的处理结果,是计算统计出AttitudeCorrectionRoll并且在采样的同时对陀螺仪采集的数据进行实时修正。值得注意的是,长期融合对于不同的机械结构(如不同大小的机架)使用类似算法的适用性有很显著的提高,且对积分稳定不漂移有不小的贡献。长期融合的基本思路是将陀螺仪采集的数据的积分结果再次积分,后执行衰减,再与加速度计采集的数据进行比较。从而得出较为准确的漂移误差,并最终修正到采样瞬时值中,执行对积分数值的累加修正。
第6步:基准点修正。上述文章提及了基准点的重要作用,及重要价值。在实际环境中,不可避免会产生由温度、噪声等引起的误差,导致基准点漂移。所以对于基准点执行实时修正补偿对于提高整个系统稳定性是非常有帮助的。基准点的修正补偿原理是,在到达了BALANCE_NUMBER的采样次数后,执行短期融合与长期融合的修正补偿之后,对比原始与执行修正之后的基准点参数信号,如果差距过大,则判断是基准点的漂移导致。根据其偏差的正负判断执行基准点修正的方位。
第7步:Yaw/Rud轴数据处理。Yaw参数代表水平旋转。对于姿态校准调节来说,Rol与Pit作用相对Yaw较强,所以优先考虑Rol与Pit的调节执行,即:优先考虑Rol与Pit的卡尔曼滤波算法执行。完成之后,本设计对于Yaw的瞬时值与积分值进行计算。
至此,基于卡尔曼滤波的姿态数据处理基本完成。得到了较为准确客观且具有代表性的实际姿态数据。如下:横滚姿态数据:Reading_IntegralGyroRoll;俯仰姿态数据:Reading_IntegralGyroNick。需要注意的是,上述两个处理之后的数据并非真实的旋转角度,而是随着最终旋转角度的增加而增加,且具有较好的跟随性与随动性。
2.2 PID算法及机体坐标系建立与分析
⑴ PID控制算法设计
PID算法是一种较为常用的自动控制算法,控制模块的前期姿态融合算法会采用卡尔曼滤波,后期算法则会采用PID算法来做最终的姿态控制[5]。
PID算法在四旋翼飞行器上的本质就是把采集到的数据和参考数据相减(图2),然后把此差值应用到系统的输入值,系统输入值就会让系统数据达到或保持在设定的参考值范围内。PID控制器具有结构简单、稳定性好、计算方便等优点。
离散系统中的位置式的PID表达式为:

公式中,KP、Ki、Kd分别为比例、积分、微分系数。error是“设定值减去当前值”。
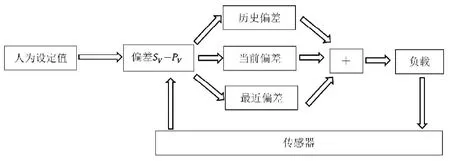
图2 PID算法流程图
在采集的数据计算中,seted为目标姿态,由遥控段设定,即:人为控制。从物理角度看,seted在最终PID表达式中对姿态控制起到正反馈作用。当seted数值变化的时候,经过PID调节器的计算,四旋翼飞行器的姿态会跟随seted的方向而变化。实际姿态数据在经过PID计算处理之后,对平衡的保持充当负反馈的作用。PID的算法过程简单来说就是不断地去调整设定的数值(人为操控的输入值)与实际姿态的通过前文卡尔曼滤波后的数值之间的关系。通过KP、Ki、Kd分别为比例、积分、微分三个角度来修正这一误差。且形式与二阶运算的解结构类似,因此使用PID算法控制二阶系统(电机控制系统为二阶系统)符合控制方程,可以较好的执行所需的控制任务。
本设计中陀螺仪、加速度传感器、磁力计都是有本身特有的参考系的,换言之,都是有方向的。当这3个与姿态采集相关的传感器均焊接到PCB板上后,以它们为基准建立坐标系。姿态数据从3个传感器采集的信息读取。焊接完毕之后,根据标志点位置推到各个传感器X、Y、Z轴的位置,并根据读取数据决定是否要对数据进行取反。
第1步:从力学角度分析得出最终控制电机的方式表达式。将四旋翼飞行器的姿态量抽象为Ail(横滚)、Ele(俯仰)、Rud(偏航)、Thr(油门)四个量,每个量包含seted和real作差以及PID算法。
第2步:根据表达式推出人为控制的方向设置。在将人为控制信号输入到PID调节器并执行PID算法前,需要将其方向调整,以至符合上文中的力学表达式。
第3步:根据力学表达式推出四旋翼飞行器运动的陀螺仪坐标系。考虑到陀螺仪是基础的姿态采集传感器,所以本设计将重点放在陀螺仪坐标的推导。根据手册标志点,将陀螺仪的坐标系与四旋翼飞行器坐标系关联,再根据力学表达式,推算陀螺仪采集信号是否需要取反。
第4步:加速度传感器的方向的正负设置。三轴加速度传感器有自身的坐标系,在构建机体坐标的过程中,判断依据主要有两种方式,分别是基于四元数法的姿态判断、基于卡尔曼滤波的姿态判断。前文提到,本设计主要采用卡尔曼滤波算法,所以下面主要讨论基于卡尔曼滤波算法的处理方式。根据陀螺仪与加速度传感器方向,确定补偿数据组。考虑到陀螺仪的动态特性较好,加速度传感器的静态特性较好,所以采用加速度传感器来补偿陀螺仪的漂移[6]。将加速度传感器采集的三个轴数据表示为Acc_Rol、Acc_Pit、Acc_Yaw,从而能更好地与陀螺仪采集的Rol、Pit、Yaw所对应。当陀螺仪沿着一个方向转动时候,加速度传感器的某一个轴的数据信息如果产生相应的变化,则这两个数据成为一个“补偿数据组”互相补偿,最终起到修正校准陀螺仪姿态数据偏差的作用。完成之后开始PID表达式的参数构建。
前文介绍了电机控制表达式,陀螺仪转动的角速度代表瞬时变化,加速度传感器采集的数据积分后得出的数据直接选作积分项。具体PID调节器构造过程如下:
第1步:计算errorn项(比例项)。errorn代表当前时刻人为给定的姿态与实际姿态的误差,用遥控器数据减去陀螺仪姿态数据来表示。采用人为给定数据减去陀螺仪姿态采集数据。需要注意的是,人为给定坐标系与姿态传感器方向需要考虑同向或者反向的问题,从而决定程序中是加号还是减号。
第2步:计算error1+error2+…+errorn(积分项)。积分项代表陀螺仪采集的旋转角速度在四旋翼飞行器长期作用的结果,可以表示四旋翼飞行器当前姿态角度。采用经过卡尔曼滤波处理的横滚姿态数据:Reading_IntegralGyroRoll;俯仰姿态数据:Reading_IntegralGyroNick这两组数据。这样处理的好处是相较于直接采用第一步中的errorn进行积分来说,漂移较小[7]。
第3步:计算errorn-errorn-1(微分项)。每次对errorn执行算术处理之后将处理结果存储为新的变量名dataOld。在下一个处理的周期中,用新的采样数据减去dataOld得到errorn-errorn-1项。
第4步:加入KP、Ki、Kd等系数。将式中的三个参数与前三步步求得的各项分别对应相乘,所得值设定为OutPutdata表达式,并最终引用于电机控制表达式。
第5步:互补滤波。本次计算处理完成后,增加互补滤波。即,对每次运算处理的结果都与前一次结果进行加权平均。
⑵ PID算法各参数的整定
为了使得PID调节器获得较好的调节效果,除了姿态数据积分处理要准确外,还需着重关注KP、Ki、Kd三个参数的整定校准。本设计将参数的整定分为2步,第1步为估算,第2步为配凑。估算过程是根据之前各个数据的范围执行理论估算,配凑过程需要不断的进行测试并根据结果进行最理想的配凑。需要注意的是KP、Ki、Kd系数的作用也需要先有定性的了解。
比例系数KP:KP系数一直对执行调节起作用,KP过小会导致系统执行调节不够明显、不够有力,过大则会导致系统出现振荡。本设计的具体调节为先设置较大的KP,然后逐渐减小并观察,当出现振荡时将当时的KP乘以0.717(经验数据),此时得到的数值再进行执行并观察有无振荡,如此循环直至系统不再出现明显振荡。
积分系数Ki:Ki主要与PID算法后期的平滑处理与收敛有关联,主要影响的是响应曲线中实际值接近定值后的部分的平滑程度,平滑程度越高系统的精细度越好。具体作用在本设计的直观结果,为在四旋翼飞行器较为稳定的状态下如果出现小范围偏移,则调大Ki;如果出现振荡且较振荡较大,则调小Ki。
微分系数Kd:增加系统的快速反应能力,增加收敛时刻的振幅。在具体调节中,有振荡则调小,反馈弱则增大。
3 实验与测试
本章主要根据设计的需要对系统环节的可靠及可行性进行实验与测试。由于本设计将PID控制比例设置为可通过Android上位机进行调节所以本设计直接进行实物调试。
3.1 Android上位机通讯实验
首先,打开四旋翼飞行器总开关,确保蓝牙通讯模块红灯闪烁,表示处于开放状态打开Android上位机的应用程序并进行连接蓝牙,本设计的蓝牙标识为BT04-A。蓝牙匹配连接成功后,四旋翼飞行器搭载的蓝牙模块红灯显示常亮,Android应用显示“蓝牙已连接到BT04-A”字样。
3.2 Android上位机控制电机测试
在Android上位机应用程序上打开电调控制测试开关,并观察四旋翼飞行器各电机运行情况(需要在测试前拆除机翼)。
3.3 Android上位机校准陀螺仪磁力计
打开Android上位机界面,开启校准模式。放平四旋翼飞行器,点击校准加速度计。观察显示的传感器数据(图3)。
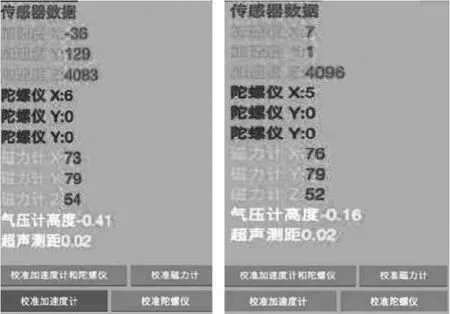
图3 校准测试前(左)、后(右)
3.4 飞行姿态自平衡测试
本设计对于姿态反馈的测试主要先测试低油门下单电机对于姿态的调节,后加大油门至30%油门观察对轴的自我稳定情况,后进行实际测试。具体步骤如下:
首先将对轴进行非刚性固定,本设计采取用无弹性的绳子绑住一对轴的机架部分,将剩余一对的电机取一端放置最低点,另一端为最高点。加大油门至5%,渐渐放平。观察低处电机在放平之前有无转动(图4)。
接着,加大油门至30%,轻微触碰自由对轴的一端,让其偏离水平,然后观察四旋翼飞行器能否回到平稳状态。本设计期望在四旋翼飞行器在油门5%的前提下,与水平夹角50°左右能有明显的响应,实验后确定PID增益为设定区间的40%左右。

图4 对姿态反馈控制的测试

图5 Android上位机控制飞行器起飞
3.5 与Android上位机的姿态同步
在空旷地带进行与Android上位机的姿态同步测试,改变搭载Android系统的移动端角度,观察四旋翼飞行器能否跟随移动端控制(图5)。
4 结论
随着工程作业目的越来越复杂,作业环境越来越特殊,四旋翼飞行器在各个领域有了更广泛的应用,同时工程研究项目对四旋翼飞行器可靠性灵敏度、以及便携程度都有了更高的要求。四旋翼飞行器的进一步简便化、轻量化的研究对于工程实践有着很高的战略意义。
本文综述了四旋翼飞行器的发展概况和发展趋势,并将卡尔曼滤波和PID算法相结合,设计出了四旋翼飞行器软件,实现了现代飞行器所需要的便捷化、高灵敏度、高精度等特点,并在最后进行了该设计的可靠及可行性进行的实验与测试,得出了该方案高效可行的结论。
