基于逐步回归分析法的炉渣-水泥-全尾砂 胶结充填体强度影响分析

张盛友，孙 伟，李金鑫

(1.昆明理工大学国土资源工程学院，昆明 650093；2.云南省中-德蓝色矿山与特殊地下空间开发利用重点实验室，昆明 650093)

0 引 言

随着金属矿浅部资源的日益枯竭，深部开采成为我国矿业发展面临的重要问题，充填采矿法作为深部开采最安全有效的方法之一[1]，在矿山中的应用比例逐渐升高。胶结充填占采矿成本的三分之一以上，其中胶结充填材料是充填成本的主要支出[2]，因此，研究低成本、高强度的充填材料已成为充填采矿法的主要研究方向之一。祝丽萍等[3]通过XRD、SEM分析对赤泥、全尾砂、水泥复合下的水化产物、微观结构进行了研究，结果表明，多重复合材料的力学性能比水泥全尾砂更加优越。樊忠华等[4]基于矿山分级尾砂存在的实际问题，开展全尾砂膏体配比试验，得出灰砂比相同时，分级尾砂与全尾砂试块强度相当的结论。贺桂成等[5]、郭利杰等[6]对不同配比的全尾砂废石水泥胶结充填体进行了实验，均表明在合理配比范围加入废石能有效提高充填体的强度。兰文涛等[7]利用半水磷石膏替代胶凝材料，为矿山创造了较好的经济效益。张睿冲等[8]基于试验结果，建立了充填配比与其响应量的高斯过程回归模型，用遗传算法对高斯过程回归模型进行多目标参数优化，得出了最优充填配比。杨啸等[9]对棒磨砂、戈壁砂、尾砂混合骨料进行正交实验，并在实验数据的基础上建立了神经网络预测模型，并分别采用极差分析和回归分析,揭示了充填体强度与混合充填骨料特征值之间的关系。高炉矿渣作为炼铁过程中的副产物[10]，具有一定的潜在活性，在矿山充填研究中具有非常广阔的前景。吴爱祥[11]、姜关照[12]等对铜炉渣进行了不同程度的激活，结果表明，铜炉渣胶凝材料满足井下充填的强度要求。董越等[13]利用钢渣替代最优配比中的矿渣测试试样的抗压强度、吸水性能和膨胀收缩性能，结果表明，钢渣取代量越高，试件抗压强度越低，吸水量逐渐升高，收缩率逐渐减小。国内外对低能耗、高强度的充填材料已经有大量报道，但大多数均集中在某单一元素对充填体强度的影响，忽略多元素耦合下的交互作用。本文通过设计不同配比实验，分析了炉渣-水泥-全尾砂耦合下的单一元素或两种及以上元素之间的交互作用对单轴抗压强度的影响。

1 实 验

1.1 原材料

实验选用四川省凉山州某铜矿全尾砂及磨细炉渣作为粗骨料，矿用P·O 32.5复合硅酸盐水泥为胶凝材料。全尾砂粒级组成曲线见图1(a)，密度为2.79 t/m3，化学成分如表1所示；炉渣粒级曲线见图1(b)，密度为3.68 t/m3，化学成分如表1所示。

表1 原料化学成分(质量分数)Table 1 Chemical composition of raw materials (mass fraction) /%

图1 粒级组成曲线Fig.1 Particle size composition curves

由图1(a)可知，全尾砂粒径在-74 μm的累计百分含量为70%，不均匀系数为9.53，曲率系数为1.26，全尾砂粒级分布范围大，尾砂级配较好，连续性较高。

由图1(b)可知，炉渣粒径在-74 μm的累计百分含量为59%，不均匀系数为23.15，曲率系数为1.85，炉渣粒级分布范围较大，级配良好，连续性较高。

炉渣化学组成是影响其活性的主要因素之一，目前仍习惯于用各氧化物质量含量之比来衡量炉渣活性的品质[14]。根据表1所示炉渣化学成分质量分数，炉渣碱性系数M0、质量系数K、活性系数Ma分别按照式(1)～(3)计算：

(1)

(2)

(3)

根据式(1)可得炉渣碱性系数M0=0.203<1，故该炉渣为酸性炉渣；由式(2)、(3)可得质量系数K<0.46，活性系数Ma为0.202，根据GB/T 203—1994《用于水泥中粒化高炉矿渣》中的规定，K不应小于1.2，K值越大，炉渣质量越好，因此本实验选用的炉渣质量较差，活性较低。

1.2 仪器及方案

实验采用YAW-300B微机控制恒应力压力试验机，此设备具有精度高，操作便捷，自动调平等优点，适用于抗压强度较小的水泥试块。实验方案采用0%炉渣(全尾砂)、10%炉渣、20%炉渣、30%炉渣质量添加量的试件在不同质量浓度、灰砂比共计24个配比下的7 d、14 d、28 d的单轴抗压强度对比分析，实验配比及强度见表2。

1.3 实验方法

实验采用尺寸为70.7 mm×70.7 mm×70.7 mm三联标准模具，实验前将模具刷一层油，拧紧模具旋钮，按配比表对水泥、尾砂、炉渣和水进行称量，搅拌均匀后灌入模具抹平，待24 h拆模标记后装入保鲜袋常温放置养护，每天早晚各喷一次水，到达规定养护时间后用压力试验机进行单轴抗压强度实验，记录实验数据。

2 结果与讨论

试块在不同炉渣掺量、质量浓度(各种固体的质量与总质量的百分比)、灰砂比下的7 d、14 d、28 d单轴抗压强度见图2和表2。

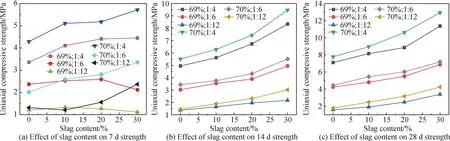
图2 炉渣掺量-单轴抗压强度曲线Fig.2 Slag content-uniaxial compressive strength curves

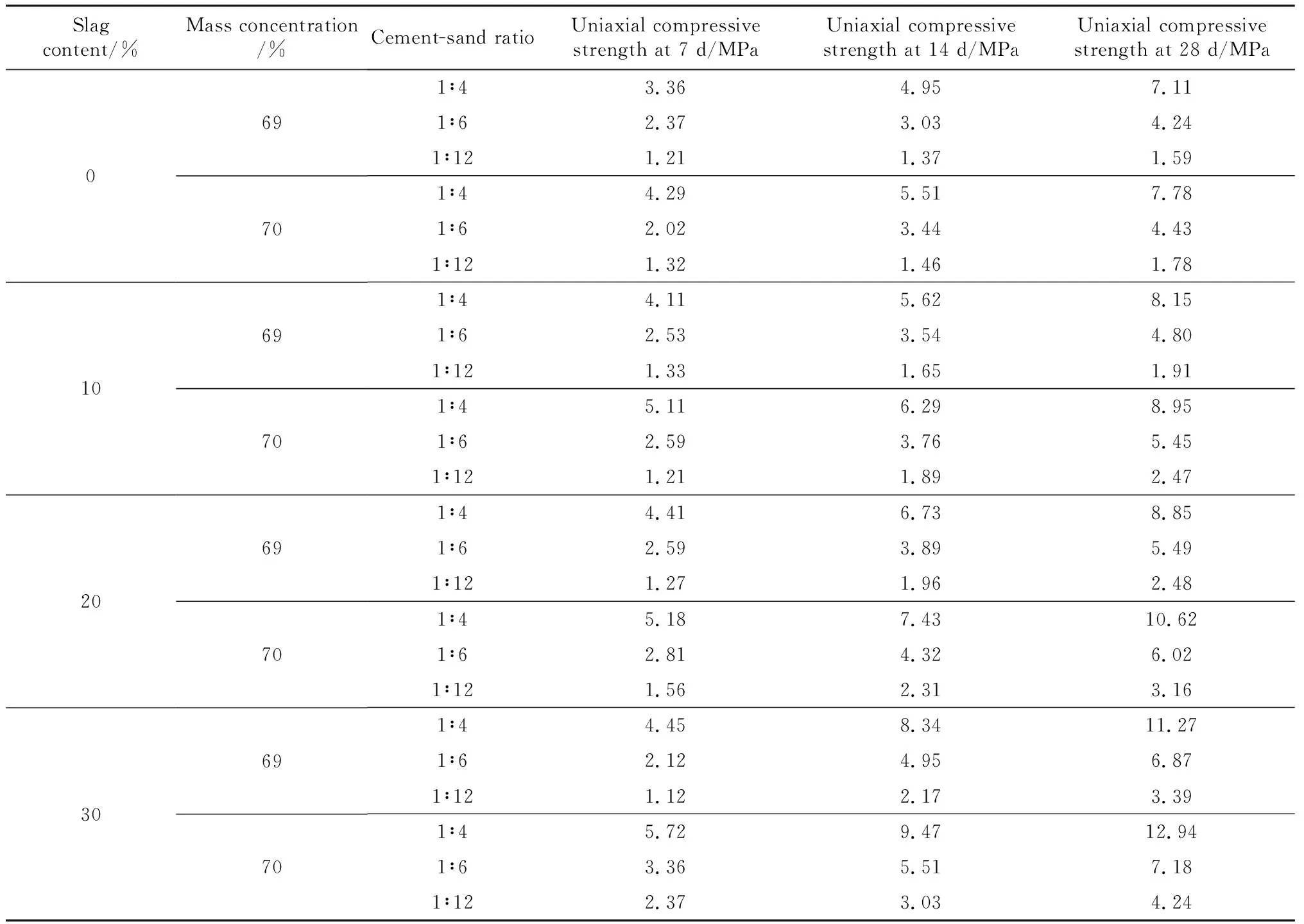
表2 不同配比的单轴抗压强度Table 2 Uniaxial compressive strength of different proportions

从图2(a)可知，质量浓度、灰砂比不变时，与未掺炉渣相比掺入10%炉渣可提升试块7 d单轴抗压强度，灰砂比越大，提升比率越大；掺入20%炉渣比10%炉渣提升强度较小，对于低质量浓度、低灰砂比甚至呈降低的走势；掺入30%炉渣较20%掺入量强度增长呈两极分化，质量浓度70%的1∶6和1∶12灰砂比的试块强度增长较快，但质量浓度69%的1 ∶6和1 ∶12的试块强度下降，灰砂比为1∶4的两组数据增长缓慢。分析其物理原因可能为炉渣比重大，颗粒较粗，比表面积小，掺入10%炉渣时，可与尾砂形成良好的颗粒级配，固体体积减小，单位体积固体分配的水泥增多，故灰砂比越大的试件强度增长越大，灰砂比达到1∶12强度几乎无影响；掺入20%炉渣时，固体体积继续减小，体积浓度减小，所以质量浓度70%的试块强度增长较小，而质量浓度69%的试块强度则几乎没变；掺入30%炉渣时，试件体积浓度较小，质量浓度69%的试件在浇模时出现少量固液分离现象，质量浓度70%的试件加入炉渣后，体积浓度适中，强度增长较大，因此加入30%的炉渣导致试块强度呈现两极分化。

图2(b)、(c)规律相似，单轴抗压强度曲线分为三部分，每部分皆由两条灰砂比相同、不同质量浓度的曲线相邻组成：1∶4的两条曲线的节点斜率相差很小，表明掺入同量炉渣增加的强度大致相仿；1∶6的两条曲线在炉渣掺量10%相邻最近，炉渣掺量20%、30%与未掺炉渣的节点斜率相差较小；1∶12的两条曲线随着炉渣掺量增加差距逐渐变大，70%、1∶12的试块强度增加较为明显。分析原因可能为灰砂比较大，水泥含量高，加入炉渣，填料浆体体积浓度变小，单位体积分配的水泥含量增加，质量浓度对试块强度增量影响较小；灰砂比较小时，水泥含量少，水化反应所需自由水较少，质量浓度对强度增长影响较大。

表3中增长率的计算公式如式(4)所示：

(4)

式中：η为增长率；σn为炉渣添加量为n%的单轴抗压强度，MPa；σ0为炉渣添加量为0%的单轴抗压强度, MPa(同一公式中的σn、σ0均在质量浓度、灰砂比相同，炉渣掺量不同时得出的单轴抗压强度)。

图3(a)中,质量浓度70%，灰砂比1 ∶6、1 ∶12的两组试块单轴抗压强度增长率随炉渣掺量增加急剧增大；质量浓度69%，灰砂比1 ∶6、1 ∶12的两组试块强度增长率则随炉渣掺量增加逐渐减小，且当炉渣掺量为30%时，增长率均为负值；灰砂比1 ∶4的两组试块强度增长率随炉渣掺量增加缓慢增长。

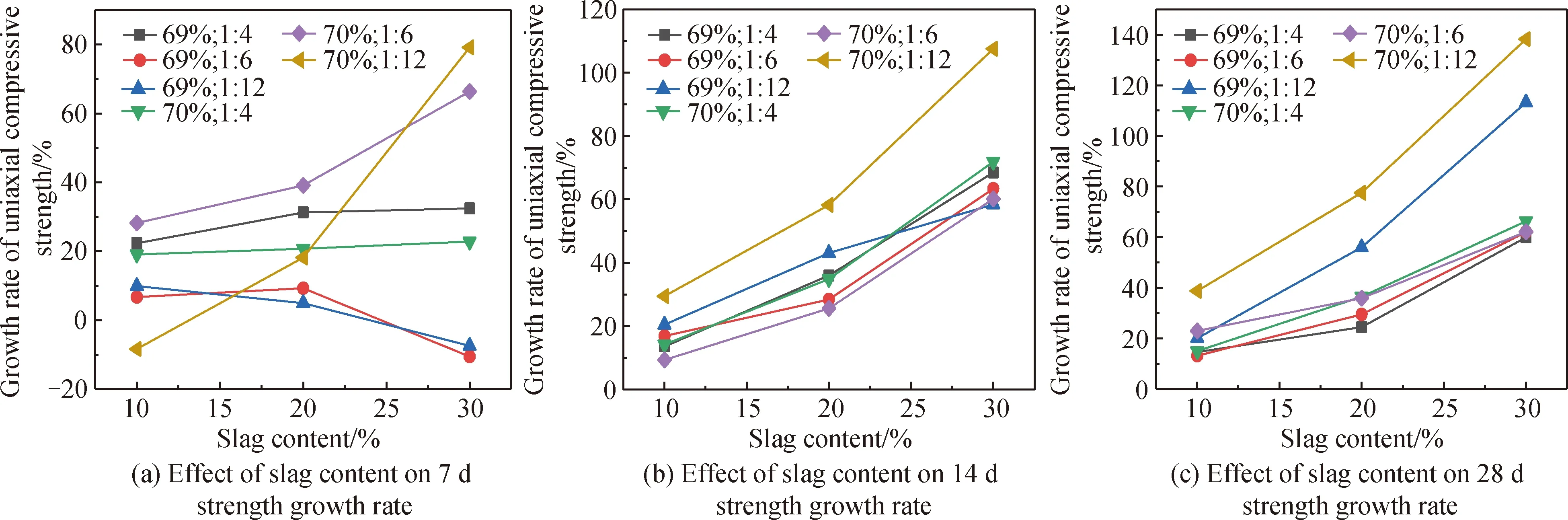
图3 炉渣掺量-单轴抗压强度增长率曲线Fig.3 Growth rate curves of slag content-uniaxial compressive strength

图3(b)中，试块单轴抗压强度增长率均随炉渣掺量增加变大，其中质量浓度70%、灰砂比1 ∶12的试块强度增长率变化尤为明显，炉渣掺量30%时增长率为107.53%，相较于全尾砂的试块强度提升一倍。

图3(c)中，灰砂比1 ∶12的两组数据增长率较大，掺入30%炉渣，强度增长率分别为107.53%和138.2%，其余数据增长率较为集中，掺入10%、20%、30%炉渣，增长率分别集中在20%、30%、60%左右。

3 逐步回归分析

在实验结果与数据分析中，得出了炉渣掺量、质量浓度、灰砂比与单轴抗压强度的简单增长关系，为更加准确分析出三个变量与单轴抗压强度的关系，使用逐步回归分析法模拟出三个变量共同作用下与单轴抗压强度的关系式。

3.1 回归步骤

逐步回归基本思想是将炉渣掺量、质量浓度、灰砂比分别设定为变量X1、X2、X3，单轴抗压强度则设定Y，Y由X1、X2、X3共同决定，先将原始解释变量X1、X2、X3及交互作用下的变量X1X2、X1X3、X2X3、X1X2X3作简单回归，得出X1X2、X1X3、X1X2X3的P值均大于0.05，对Y不显著，应舍去。得出其余变量对模型结果的贡献大小，以最大贡献变量的回归方程为基础，将其余解释变量依次引入回归模型，每引入一个解释变量都要对其进行F检验，然后对已选入的解释变量进行T检验，当新加入的解释变量导致原先引入的解释变量不再变得显著时，则去掉新加入的解释变量，使模型中每个解释变量始终处于显著状态，以此为循环，直到加入所有的解释变量且模型中没有不显著的变量为止，以保证回归方程的最优性。

3.2 回归结果及分析

本次回归采用SPSS 22.0软件对原始数据因子变量进行相关性分析，结果如表4所示。

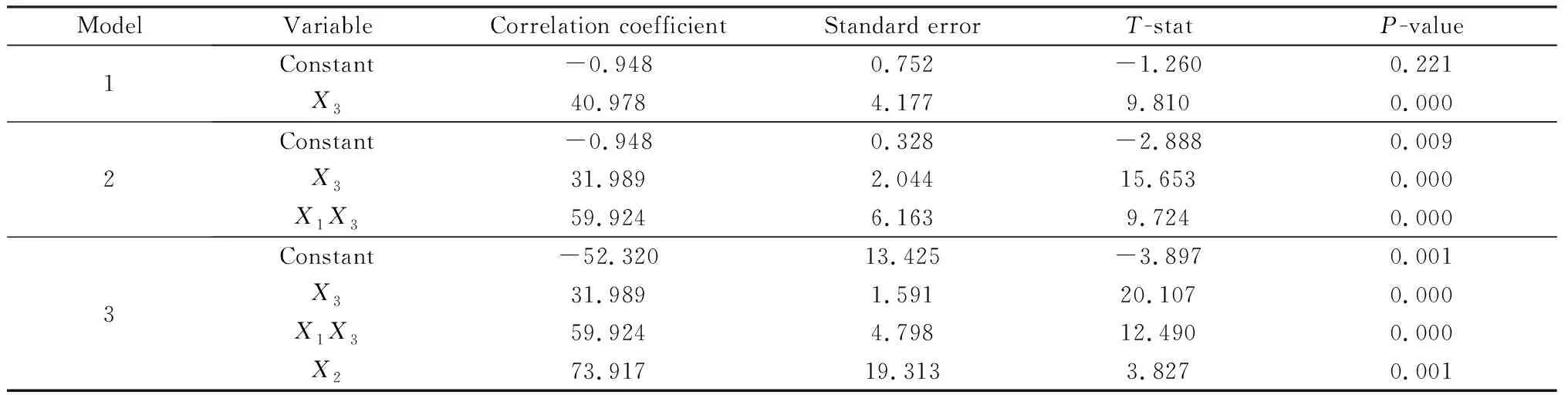
表4 线性回归分析结果

从表4可知，模型分三次建立，由逐步分析前的简单回归显示X3对Y的影响最大，因此在模型1中以X3为基础进行回归，回归结果中显示X3的P值远小于0.05，表明X3对Y非常显著，但由于只带入了X3一个解释变量，无法使数据回归结果接近实验值，故常量表现为不显著，模型1的回归方程为Y=40.978X3-0.948;在模型1中引入X1发现P值大于0.05，表明X1对Y不显著，应舍去。通过实验数据可知炉渣对强度有显著影响，两者相悖，考虑是否为炉渣和水泥耦合情况下导致对强度有较大影响，故在模型1中引入X1X3，结果显示在炉渣和水泥耦合作用下对强度影响非常显著，整体模拟效果远好于模型1，模型2的回归方程为Y=31.989X3+59.924X1X3-0.948；在模型2的基础上引入X2，P值均趋近于0，表明各解释变量对Y非常显著，输出调整后的拟合度为97.76%，说明此模型拟合得非常好，回归方程整体显著，故输出最终的回归方程为Y=73.917X2+31.989X3+59.924X1X3-52.320。

3.3 回归方程检验

为检验3.2节中回归方程的回归精度，带入X1、X2、X3的具体数值，得出28 d单轴抗压强度回归值，将实验值与回归值引入Origin中，得出两组数据的对比曲线，如图4所示。

从图4可知，相同配合比条件下，28 d实验强度曲线分布在回归曲线两侧，距离回归曲线非常接近，验证了回归方程的可靠性；回归曲线随着炉渣掺量增加平稳缓慢上升，由于实验条件、人为因素等误差影响导致曲线有少许离散点。基于回归方程可靠的基础上，以炉渣掺量、质量浓度、灰砂比为变量因素，单轴抗压强度为响应量，设计响应分析因素水平如表5所示。

图4 回归精度检验曲线Fig.4 Regression accuracy test curves

将表5中的数值及回归公式计算出的单轴抗压强度代入Design-expert中的BOX-Behnken，选择2FI模型分析，得方差分析如表6所示。

表5 响应面分析因素水平表Table 5 Response surface analysis factor level Table

表6 响应面2FI模型方差分析表

从表6可知回归选用的模型为2因素交互模型，回归模型P-value<0.000 1，表明此模型整体非常显著；单因素A、B、C分别代表炉渣掺量、质量浓度、灰砂比，且P值均小于0.000 1，表明单因素对响应量的影响均非常显著；两两交互因素中唯有AC交互显著；失拟项大于0.05，不显著，因此回归模型符合要求。由输入值回归的最终方程表达式为Y=0.015X1+73.9X2+31.988X3+59.92X1X3+4.144×10-12X1X2+9.348×10-14X2X3-52.29(其中X1为炉渣掺量；X2为质量浓度；X3为灰砂比)，从式中可知，炉渣掺量与质量浓度、质量浓度与灰砂比交互的数值可以忽略不计，对整体结果无影响，调整后的R2为0.999 8，回归效果极其显著；回归模型选择的最优配比为炉渣掺量15%、质量浓度69%、灰砂比1∶12；两两因素交互下对响应量-单轴抗压强度的影响如图5所示。

图5 两因素交互下对单轴抗压强度的影响Fig.5 Influence of interaction of two factors on uniaxial compressive strength

图5中，固定参数均取变量的中间值，两因素交互作用下，灰砂比和炉渣掺量交互对单轴抗压强度的变化跨度最大，最大值为11.913，最小值为2.077；质量浓度与炉渣掺量交互对单轴抗压强度影响最小，最大值为8.505，最小值为4.025。

对比逐步回归分析法与响应曲面法，回归的最终方程表达式基本一致，响应面法可以通过2D、3D图，更为直观地表现出两因素交互下对单轴抗压强度的影响。

4 结 论

(1)7 d单轴抗压强度在炉渣掺量30%时呈现两极分化，质量浓度70%，灰砂比1∶6、1∶12的两组试块强度增长较大，而质量浓度69%，灰砂比1∶6、1∶12的两组试块强度呈降低趋势；14 d、28 d的炉渣掺量-单轴抗压强度曲线变化规律一致，灰砂比越大，炉渣掺量越多，强度增长越大。

(2)炉渣掺量较大时，单轴抗压强度对质量浓度有一定要求，炉渣掺量越多，不同质量浓度的试件单轴抗压强度差距越大，例如炉渣掺量30%、质量浓度70%、灰砂比1∶6、1∶12的试件强度增长率较大，而炉渣掺量30%、质量浓度69%、灰砂比1∶6、1∶12的试件增长率为负值；28 d强度最高增长率为138.2%、最低增长率为13.2%。

(3)逐步回归分析显示单一元素对单轴抗压强度的影响权重依次是质量浓度、灰砂比，炉渣掺量影响不显著；两种及以上影响因素交互作用下仅炉渣掺量与灰砂比交互对强度影响显著；响应曲面法与逐步回归分析法所得结论基本一致，验证了回归方程的可靠性；回归的最终方程为Y=73.917X2+31.989X3+59.924X1X3-52.320，回归拟合度97.76%，可用于该矿山充填现场。