聚类集成中的外部有效性指标评估研究
2021-01-11于祥
于 祥
(南京财经大学 信息工程学院,江苏 南京 210023)
数据聚类或无监督学习是一个重要而困难的问题,许多应用领域使用聚类技术来组织和发现数据结构,如数据挖掘、信息检索、图像分割和机器学习等。现实世界中,聚类可能会出现不同的形状和大小,数据中的噪声也可能掩盖数据中存在的真实结构。
虽然存在大量的聚类算法,但是很难找到一个能够处理所有簇形状的单一聚类算法。受分类集成研究的启发,人们开始关注聚类集成方法的研究。聚类集成在各个环境中都很有用,它将几个聚类组合在一起可以提高结果的质量和稳健性,实现知识重用,也可以组合来自分布式计算的各个结果。
聚类集成本质上是一个组合优化问题,许多文献提出了用于求解共识聚类的方法,如共联矩阵法[1-3]、超图法[4]、互信息法[5-6]、投票法[7-9]、混合模型法[10]、基于Kmeans法[11]等。Lu等[12]利用基于配对计数的聚类外部有效性指标来组合多个基础分片求解共识聚类,该方法使用了3种共识函数用于聚类集成。
外部聚类有效性指标通常被解释为“真实”聚类与候选聚类之间的相似性(或非相似性)度量。“真实”聚类提供了与候选聚类比较的基准,候选聚类与“真实”聚类越相似,则该聚类越接近数据中的标记结构。
本文设计一个模拟退火优化框架来评估用于引导聚类集成的11种聚类外部指标,为基于外部有效性指标的聚类集成算法选择合适的共识函数提供指导。
1 聚类外部有效性指标
本文利用11种广泛使用的外部指标,这些指标可以划分为配对计数指标和信息论指标,它们的共同点是可以通过列联矩阵进行计算。
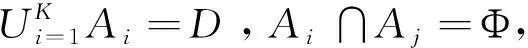
构件分布详见平面图,构件截面大小详见表1。

表1 列联矩阵Table 1 Contingency matrix
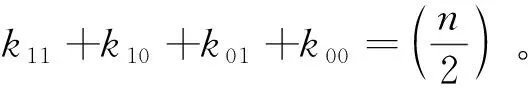
表2列举了11种外部有效性的指标,前面9种是从相关研究[13,15]中挑选的配对计数指标,这些基于配对计数的聚类外部指标是由上述4种配对类型计算而来的。值得注意的是,一些被选择的指标等价于其他指标,如Rand Index(MR)等价于4种指标,即Mirkin metric(MM)、HubertΓII(MΓ′)、Gower & Legendre(MGL)和Rogers & Tanimoto(MRT);Jaccard coefficient(MJ)等价于2种指标,即Dice(MD)和 Sokal & Sneath II(MSS2)。所以本文的研究包含了文献中的17种聚类外部指标。


表2 外部有效性指标Table 2 External validity measures

2 外部指标聚类集成算法框架
利用聚类的外部指标将聚类集成定义为组合优化问题。对于具有n个对象的数据集D,任何一个分片都能表示为一个簇标记向量π=(Lπ(x1),Lπ(x2),…,Lπ(xn))T,其中Lπ将每个对象映射到集合{1,2,…,K}中的某个簇标记。
给定一组r个分片的集合П={π1,π2,…,πr},其中πq是一个簇标记向量,1≤q≤r,可以将聚类集成的目标函数设置为单个分片π和分片集合П之间的度量,即
(2)
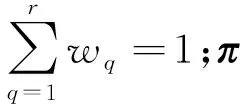
聚类集成的目标是最大化目标函数M(π,П)。为了从多个分片П中找到共识聚类,可以通过单个对象的簇标记改变来最大化目标函数M(π,П),即对于聚类A,从数据集D={x1,x2,…,xn}中随机选择一个对象xt,然后将它的标记Lπ(xt)=i更改为另一个标记k,将它从一个簇Ai移动到另一个簇Ak。
令n和n′分别表示对象xt移动前后列联矩阵中的值。对于单个对象的簇标记改变,如果i≠k会导致以下更新:
(3)

(4)
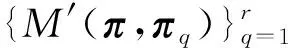
为了避免局部最优,本文进一步考虑模拟退火算法来决定是否选择单个对象簇标记的改变Lπ(xt):i→k。在温度T下,选择单个对象簇标记改变的概率计算如下:
(5)
式中:△M=M′(π,П)-M(π,П)。

下面给出基于模拟退火的聚类集成算法框架,其伪代码如表3所示。
表3伪代码中,外层循环的停止条件为:两个连续的循环中没有一个对象的簇标记更改。
3 几种算法的性能比较
3.1 实验设置
现用基于模拟退火算法的聚类集成算法框架评估11种聚类外部指标引导聚类集成的性能,并与其他聚类方法对比,验证算法的有效性。实验设置如下:
(1)实验环境:在windows 8操作系统、Intel Core i7-4790 CPU(主频3.6 GHz,8核)、16 GB内存的计算机上,在IntelliJ IDEA2017环境下,采用Scala语言编程。
(2)数据集:在UCI和TREC数据库中选取10个数据集,其中ecoli数据集中只包含2个样本的2个类簇被作为噪声去除。这些数据集的信息如表4所示,其中变异系数[16]刻画了类簇的离散度,变异系数越大表示类簇越失衡。

表3 基于模拟退火的聚类集成Table 3 Cluster Ensemble Algorithm via Simulated Annealing
(3)评价指标:利用标准化互信息(NMI)来验证算法的性能。
标准化互信息的指标MNMI计算如下:
(6)
式中:n为样本总数;ni.、n.j分别是属于簇i、簇j的样本个数;nij是既属于簇i又属于簇j的样本个数;MNMI值的范围是[0,1],其值越大表示算法结果与标准结果越相似。
3.2 实验过程及结果
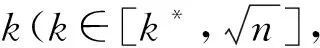

表4 数据集信息Table 4 Details of the data sets
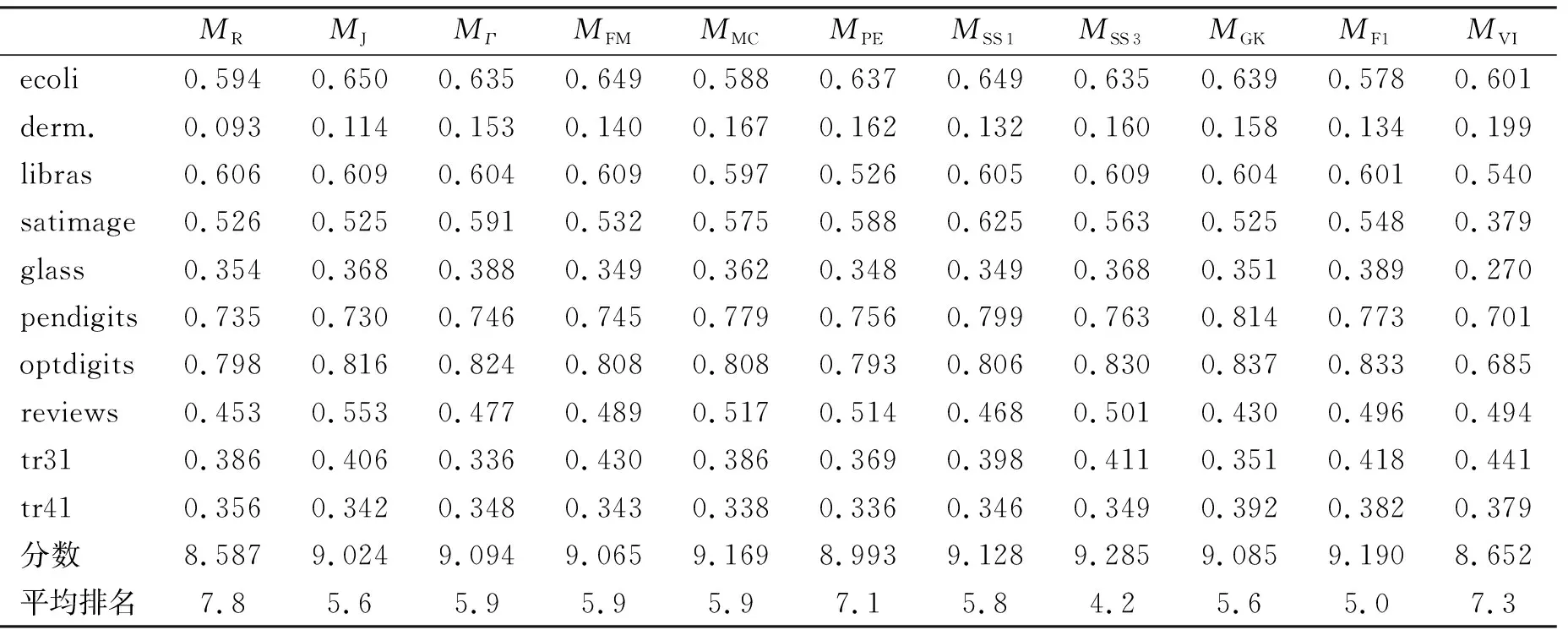
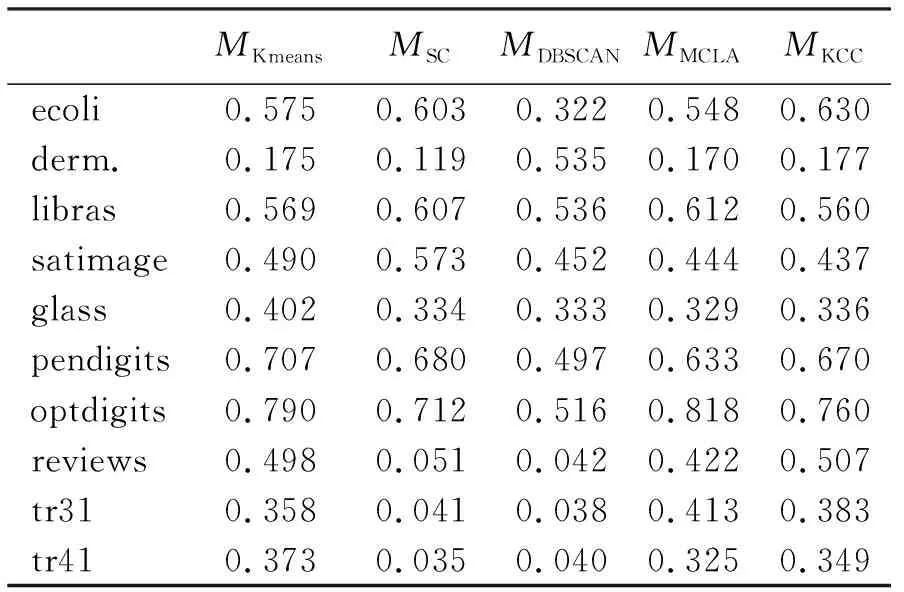
为了有效实现基于模拟退火的聚类集成算法,必须选择簇标记改变的概率阈值P0(0 下面通过上述两种方式综合评估外部指标应用在聚类集成算法中的性能。利用基于模拟退火算法的聚类集成算法对表2中11个指标进行聚类集成的性能试验时,为了客观对比不同指标的聚类性能,将每种算法独立运行20次,评价指标取平均值,试验结果如表5所示。运用基于Kmeans的聚类集成算法[11](MKCC),基于图的聚类集成算法[4](MMCLA),以及经典的Kmeans(MKmeans)、谱聚类SC(MSC)和密度聚类DBSCAN(MDBSCAN)算法对10个数据集进行性能指标试验时,得到结果如表6所示。 表5 聚类验证结果(MNMI)Table 5 Cluster validation results (MNMI) 表6 对比方法的聚类验证结果(MNMI)Table 6 Cluster validation results for comparison methods(MNMI) 根据表5、表6,得到10个数据集上分别表现出最优性能的算法,如表7所示。 从表5可以看到:11个指标中有7个指标至少在一个数据集上表现出最佳性能,其中MJ和MGK在3个数据集上性能最好,MVI在2个数据集上性能最好,MFM、MSS1、MSS3和MF1在一个数据集上性能最好;从分数上看,MSS3的分数最高,其次是MF1、MMC和MSS1,而MR的分数最低,同时MVI和MPE分数也较低。显然尽管MVI在2个数据集上性能最好,但是总体分数表现较差;而MMC没有在任何数据集上表现出最佳性能,但是综合分数却较好;MJ和MGK虽然在3个数据集上性能最好,但是综合分数却稍逊于MMC和MSS1。 表7 数据集上性能最优的算法Table 7 Algorithm with the best performance on the data set 从排序角度也可以看出与分数排名大致的结果,即性能最好的指标是MSS3,平均排名为4.2;其次是MF1、MJ和MGK,分别排名为5.0,5.6和5.6。平均排名靠后的指标主要有MR、MVI和MPE,其中MR平均排名最后一位,其次是MVI。 综上所述,在基于模拟退火的聚类集成框架中,MSS3、MF1、MMC、MSS1、MJ和MGK等指标性能表现较好,其中MSS3获得最高的分数和最好的平均排名;而MR、MVI和MPE指标在算法中的性能表现相对较差。 从表6、表7可以看出:在10个数据集上,基于模拟退火的聚类集成算法在7个数据集上表现最好,而DBSCAN、MCLA、 Kmearns算法则在其余3个数据集上表现最好。 针对聚类外部有效性指标可以将聚类集成问题定义为一个组合优化问题,设计了一种基于模拟退火优化的聚类集成算法框架,并以11种广泛使用的聚类外部有效性指标为目标函数引导聚类集成;在UCI和TREC数据库中选取10个数据集进行几种算法的外部指标聚类性能评估实验,结果表明:MSS3指标从整体性能表现上最适合用于引导聚类集成,可以作为算法默认的共识函数,而MR、MVI和MPE指标的聚类性能整体而言相对其他指标表现较差;基于模拟退火优化算法的聚类集成算法在7个数据集上优于其他聚类方法,而DBSCAN、MCLA、Kmearns算法则在其余3个数据集上表现最好,即基于模拟退火优化算法的聚类集成算法是有效的。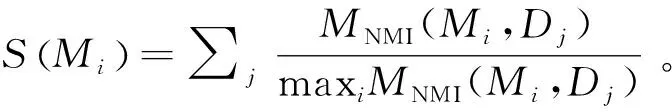
3.3 聚类外部指标的性能评估

4 结论
