基于模糊PID控制器的旋流泵调速控制

高礼科，倪福生，蒋 爽

（1.河海大学 机电工程学院，常州213022；2.河海大学 疏浚技术教育部工程研究中心，常州213022）

旋流泵的无阻塞性和耐磨性使其广泛用于复杂介质的输送[1]。由于结构问题，泵体内会产生回流和旋涡，使泵效率降低[2]，也使管道中泥浆流速不稳定，影响输送效率。管道流速控制问题成为了清淤作业中亟待解决的问题。

国内多位学者对流速控制进行了研究。其中，文献[3]针对泥浆管道输送系统流速控制，提出了一种无模型自适应前馈控制，控制效果良好；文献[4]针对管道输送流速对象，提出了一种单神经元网络自适应预估控制。以上方法虽能有效控制其控制对象，然而有的控制效果不很理想，部分模型也较简单，无法应用于复杂场合中。

旋流泵调速系统作为非线性、参数时变、有较大时滞的被控对象，要对其进行稳定控制，就要选择性能较高的自适应控制器。故在此采用模型精度要求低、响应快、稳态精度好的模糊PID 来控制调速系统[5-6]，并与传统PID 进行对比，以期改善管道输送的稳定性和安全性。此外，还设计了一种基于C#的监控界面来对实验平台进行开、闭环控制及参数的调整、监测等。

1 疏浚旋流泵调速实验台的建模分析

旋流泵的结构如图1 所示。

图1 旋流泵结构解剖图Fig.1 Structure anatomy of cyclone pump

在此，以河海大学疏浚实验室中的旋流泵输送实验平台为对象，进行调速控制系统的设计。该实验平台主要由变频器、电动机、流量计、压力传感器、差压传感器和旋流泵、管道、加砂收砂等装置组成，如图2 所示。通过该实验台可以进行管道输送自主调速试验、泥泵特性试验、管道磨损试验等。

图2 调速实验平台Fig.2 Speed regulating experiment platform

对整个疏浚旋流泵调速系统进行建模，即除控制器外所有的执行和测量变送装置，主要包括变频器、电动机、旋流泵和流体输送管道。电动机带动旋流泵工作时，流体从进口被吸入经过旋流泵从出口流出，因此旋流泵出口处的流体流速是被控变量。通过调节变频器频率可以控制流体流速，因此频率是控制量，也就是输入量。

电动机作为执行装置，将频率信号转化为转速，通过控制转速来控制被控对象；被控对象是旋流泵及管道输送装置，即通过控制旋流泵的转速来控制管道中流体的流速（即输出量）；反馈装置是流速传感器，将实时流速信号传送给比较器与给定流速进行比较，形成闭环控制系统。

疏浚旋流泵调速控制系统的结构如图3 所示。

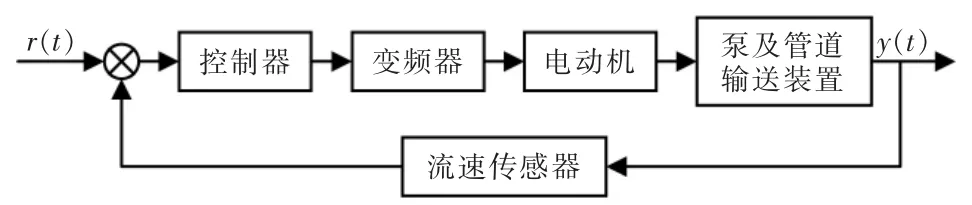
图3 控制系统结构框架框图Fig.3 Structure frame block diagram of control system

在此，试验数据通过以变频器输入的阶跃频率响应试验得到，通过试验数据即可完成对被控对象的数学建模，通过最小二乘法[7]及赤池信息量准则（AIC 准则）对实验台系统进行系统辨识。

利用最小二乘参数辨识建立的数学模型不包含时滞部分，具体可供选择的数学模型有一阶模型、二阶模型和三阶模型。即

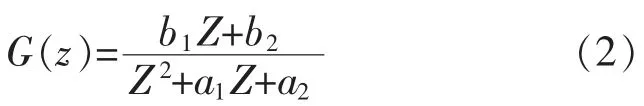
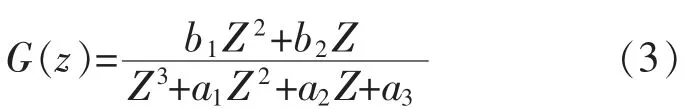
运用最小二乘法分别得到这3 个模型的参数估计，即

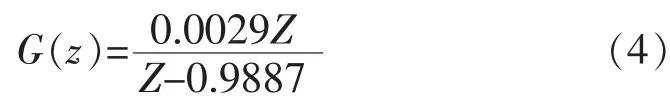
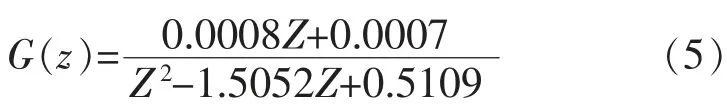
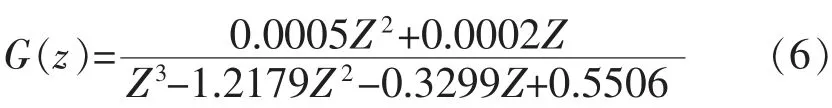
利用AIC 准则，在样本量n＝1750 的情况下，得到：

一阶模型的均方差为J＝0．2462，AIC＝-2449；

二阶模型的均方差为J＝0．1415，AIC＝-3414；

三阶模型的均方差为J＝0．2002，AIC＝-2805。

因此，模型阶次为AIC 最小的二阶模型。通过最小二乘参数辨识经过3200 次递推，在采样时间t＝0．1 s 的情况下，除时滞部分外的数学模型辨识结果为

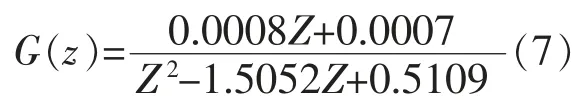
对不同输入的试验数据进行分析，发现时滞部分在不同情况下略有不同，但总体时滞时间在3～5 s范围内变化。可以取中间值4 s 作为时滞时间，如图4 所示，故最终数学模型为

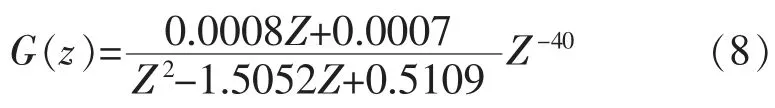
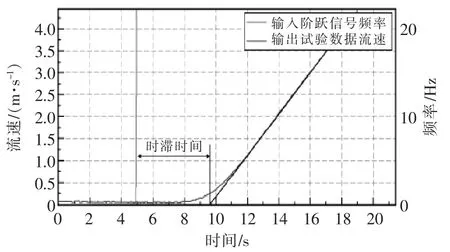
图4 时滞时间Fig.4 Time delay

通过使用F 检验法对该模型进行评价，得到的结果符合要求。

2 PID 参数整定及仿真

2.1 传统PID 参数整定

Z-N 临界比例度法由Ziegler 和Nichols 学者提出。该方法只需确定临界比例增益Ku和临界振荡周期Tu，即可根据公式完成PID 参数整定。采用Z-N 临界比例度法，通过表1 提供的整定公式进行整定并修正。修正后，得Kp＝8，Ki＝1，Kd＝8，此时具有较好的控制性能，但是超调量较大，PID 响应曲线如图5 所示。

2.2 模糊PID 控制器

输入是给定值与反馈信号的偏差e，以及偏差的变化率ec；输出是Δkp，Δki，Δkd。将这3 个输出变量分别与PID 调节器的初始参数值相加，从而实现参数自整定。模糊PID 控制器结构如图6 所示[8-9]。

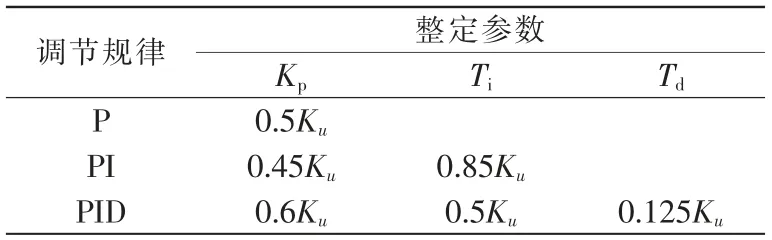
表1 Z-N 临界比例度法整定公式Tab.1 Setting formula of Z-N critical proportion method

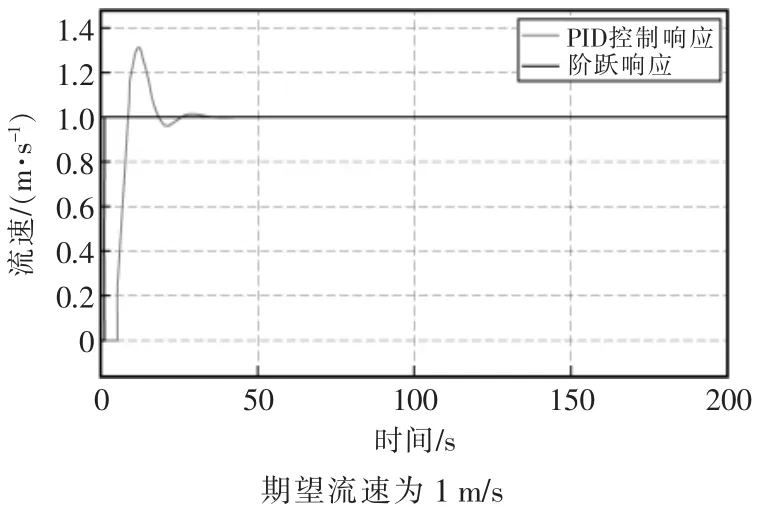
图5 PID 响应曲线Fig.5 PID response curve

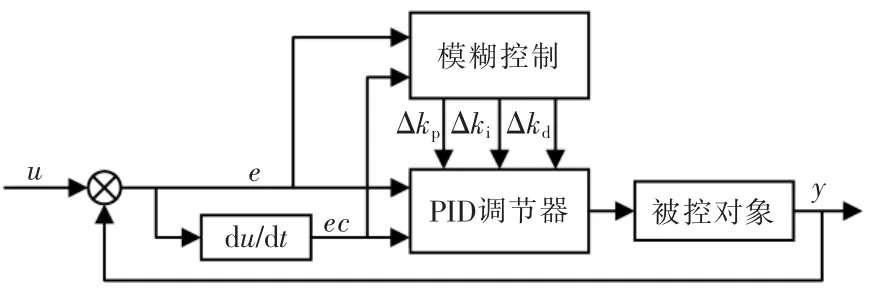
图6 模糊PID 控制器结构Fig.6 Structure of fuzzy PID controller

控制器根据式（9）来更新KP，KI，KD的值，即

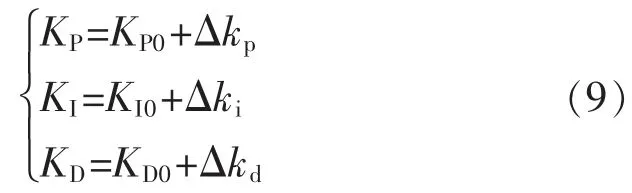
式中：KP0，KI0，KD0分别为PID 控制器的比例KP，积分KI和微分KD系数；KP，KI，KD分别为PID 调节器最终输出的比例、积分、微分参数。

2．2．1 模糊变量论域的确定

对于变量e，因给定流速最大为7．65 m/s，所以偏差范围最大为［-7．65，7．65］。实际过程中偏差很少达到最大值，因此论域可设为［-6，6］。将论域划分为7 个子集，隶属度函数均为三角形函数。ec的论域为［-1，1］，Δkp的论域为［-1．5，1．5］，Δki的论域为［-0．1，0．1］，Δkd的论域为［-1．5，1．5］。

2．2．2 确定模糊控制规则

模糊控制规则是模糊控制器的关键。基于专家总结的经验，以及大量前人总结的Δkp，Δki，Δkd与e，ec的关系，部分变量的控制规则见表2。

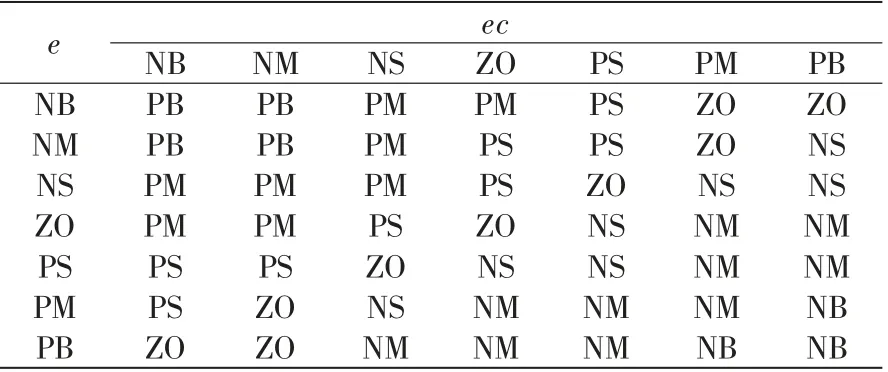
表2 变量Δkp 的控制规则表Tab.2 Variable Δkp control rules table

2.3 基于MatLab 的控制仿真对比

在此使用MatLab 中的Simulink 功能，对PID控制和模糊PID 控制进行仿真，2 个PID 控制器建模如图7 所示。

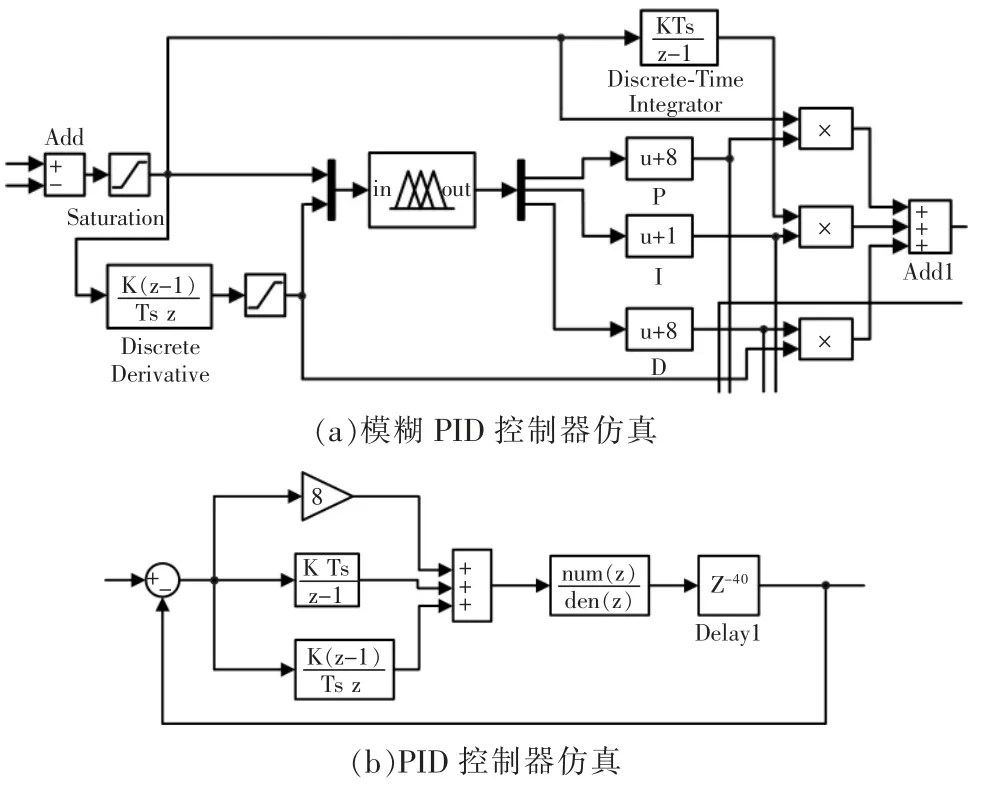
图7 MatLab 对比仿真模型Fig.7 MatLab comparative simulation model

仿真时间为500 s，因为被控对象是离散的数学模型，所以其中各控件的采样周期都是0．1 s。输入信号使用阶跃信号的叠加，信号从小到大依次为1，3，5，7 m/s。为了显示模糊PID 算法的控制过程，仿真结果需要显示2 种系统的响应过程，还要显示PID 中3 个参数的调节过程。最终结果分别如图8和图9 所示。

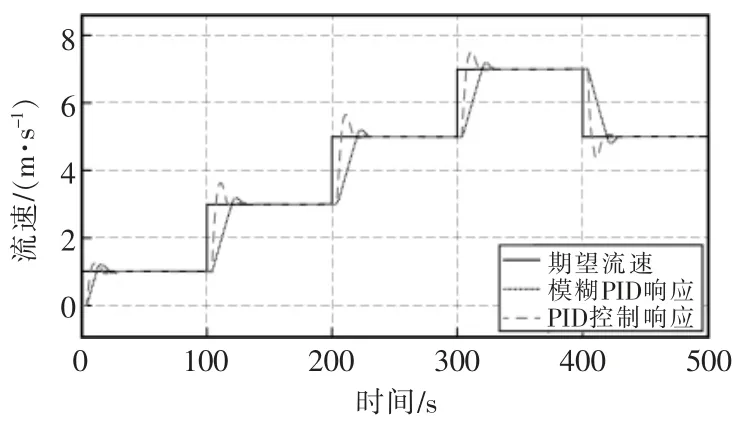
图8 模糊PID 控制与PID 控制的响应曲线Fig.8 Response curves of fuzzy PID control and PID control

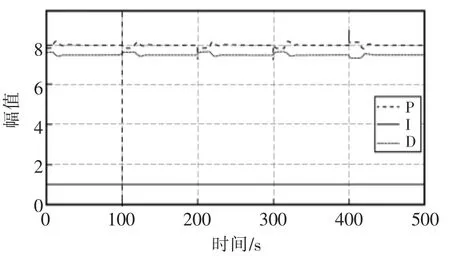
图9 PID 参数调节过程Fig.9 PID parameters adjustment process

从稳态误差、 超调量和调节时间三方面，对2种不同控制进行效果对比。对比结果显示，模糊PID控制具有更小的超调量，这主要是因为模糊PID 控制可以根据当前情况进行PID 的调节。以100 s 时变化的阶跃信号为例，此时给定信号突然增大，模糊PID 控制器通过降低比例增益增加系统稳定性，同时也会降低响应速度。通过对PID 参数进行整定，模糊PID 控制使得系统输出更加稳定，超调量更小；PID 控制则无法改变参数，不能根据外界条件的变化做出相应反应，因而控制效果并不理想。控制效果对比见表3。

表3 模糊PID 与PID 控制效果的对比Tab.3 Comparison of fuzzy PID and PID control effect

3 C#监控系统设计

运行调速系统时，为了直观的体现控制算法的作用，需要一款监控界面来展现实际流速和期望流速的差距，故在此利用C#对监控系统进行编程。C#是一种安全、较稳定、简单易操作同时不失效率性和鲁棒性的面向对象编程语言。它综合了VB 简单的可视化操作和C++的高效率运行性，使程序编程更加简单明了[10]。

下位机选用西门子S7-1500PLC，上位机通过路由器实现与下位机PLC 的信号通讯，通信协议采用OPC 协议，采用SIMATIC NET 对PC 站进行组态，相对于下位机自带的组态软件，C# 编写的界面更加简洁、清晰、美观，程序可移植性高，功能更加多样化。该监控界面能实时监测调速系统的相关信息，并将调速系统产生的数据可视化，功能界面如图10 所示。

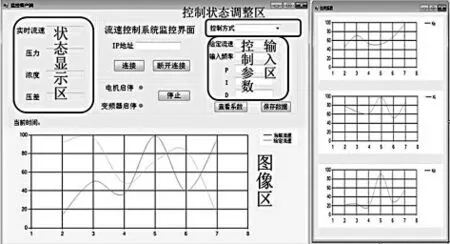
图10 功能界面Fig.10 Functional interface

该监控系统具有实时显示、实时控制和与下位机PLC 的通信等三方面功能。在系统运行过程中，监控系统实时显示流体流速、流体浓度、管道压力和差压的数值，其中流速是最重要的显示量。

为更直观的感受控制的性能，还需绘制流速的实时曲线图。监控系统有手动和自动2 种控制方式，手动模式可直接输入频率来调整，此外，根据不同情况，也可自行调整PID 参数。同时，为了体现模糊PID 控制的调节过程，PID 三个参数的变化过程也会用曲线直观展现出来，如图10 所示。

为了防止现场的突发情况，需要设置急停按钮控制电机的启动和停止，还需要明确变频器和电机的运行情况，可以用指示灯的亮灭来体现。

综上所述，模糊控制器通过对PID 参数的自适应调整成功地对流速进行了控制，使得系统输出的流速更加稳定，提高了管道输送系统的性能。将模糊PID 控制的仿真结果与传统PID 控制结果进行对比，结果显示模糊PID 控制的超调量远小于PID控制，调节时间两者相差不大，且两者均没有稳态误差，证实了模糊PID 控制算法的有效性。

旋流泵调速系统工作时，基于C# 的监控平台能实时地对系统的流速进行设置，对系统的相关参数能够进行实时监控，并将系统的期望流速和实际流速以曲线形式表现出来，更加直观地表现控制算法的有效性。

4 结语

通过系统进行频率阶跃响应得到的数据对系统进行建模，采用自适应能力强、响应速度快模糊PID 控制算法对系统的流速进行控制。通过试验仿真验证了所提方法能使泥浆流速保持稳定，保证管道输送效率。后续将在清水仿真的基础上，采用砂水混合物进行模型试验，再对仿真效果和监控系统进行试验验证，尝试采用神经网络、模型预测控制等其他先进的控制算法对系统进行寻优控制。