桩锚支护结构在路堑边坡开挖过程中的力学行为特性

万小龙， 李 聪，， 蔡亚峰， 李 宇， 林宇亮

(1.中国建筑第五工程局有限公司， 湖南 长沙 410117； 2.中南大学 土木工程学院， 湖南 长沙 410083)

0 引言

随着我国城市化地不断推进，城市用地紧张，用地矛盾突出的情况时有发生。城市区域内边坡或基坑开挖经常遇到施工空间小、周边环境复杂、重要建筑物多、无放坡空间等情况。桩锚支护结构因其突出的优势而被广泛应用于各类边坡和基坑工程中，近年来更是成为城市复杂条件下边坡支护工程的首选支护形式。

关于桩锚支护结构的力学原理和工作性能，已有很多学者做过相关研究。肖武权等[1]进行了深基坑桩锚支护结构内力和变形的现场试验，得到了排桩内力和变形的分布规律。蔡袁强等[2]运用岩土工程二维有限元软件PLAXIS 进行了深基坑开挖全过程的模拟，得出了桩体变形和弯矩的分布规律，以及支撑轴力的分布规律。周勇等[3]深入考虑桩锚支护结构和土体之间的协同作用，改进了桩体内力计算的方法，并通过数值模拟验证了该方法的正确性。王明龙等[4]采用数值建模的方式，着重讨论了深基坑桩锚支护中桩内力变化规律。伊晓东等[5]运用有限元软件ABAQUS进行了土岩二元地区深基坑桩锚支护结构变形分析，得出了土岩二元基坑支护中桩体的变形规律。

从以往学者们所做的研究来看，大多都只对基坑工程中的桩锚支护进行研究，而对边坡工程中的桩锚支护则涉及较少。本文基于长沙市龙塘小学-某大学间支路路堑边坡支护工程实例，采用FLAC3D软件进行数值模拟分析，对路堑边坡开挖过程中桩体变形和受力的变化规律进行研究。

1 工程概况

龙塘小学 — 某大学间支护建设工程的起点为万家丽北路，终点为湘龙路，设计路线全长1.3km。项目路基处理以挖方为主，K0+205～K0+525、K0+682～K0+965左侧路堑边坡地质组成主要为粉质粘土和强风化板岩，遇水易受冲刷和软化，地质情况一般。部分边坡切深达14m，且坡顶有重要的建筑物距道路红线较近，受该大学侧用地限制，无较大放坡空间。边坡为永久性支护，设计使用年限为50 a。边坡安全等级为一级，重要性系数取值γ0=1.1。

根据该工程地质详细勘察报告，场地地层分布自上而下依次为： ①粉质黏土，层厚1.50～10.00m；②中风化砾岩，最大揭露厚度为20.5m；③ 强风化板岩，最大揭露厚度为22.3m；④ 中风化泥质板岩，最大揭露厚度为9.7m。此外，本线路段所有钻孔均未见地下水。

2 边坡支护设计方案

选取地质条件较差、边坡支护高度较大、综合安全系数较小的K0+490～K0+525段进行分析。该路段边坡施工影响深度范围内土质分为2层，上层为硬塑粉质黏土层，层厚为4.12m；下层为强风化泥质板岩。考虑到边坡开挖深度较大，该段边坡工程采用桩锚支护结构形式，一共设置5排预应力锚杆，桩间距为2.0m，采用圆形桩，桩长24.5m，直径1.0m，冠梁的截面尺寸均为1.0m×0.8m。边坡支护剖面见图1。

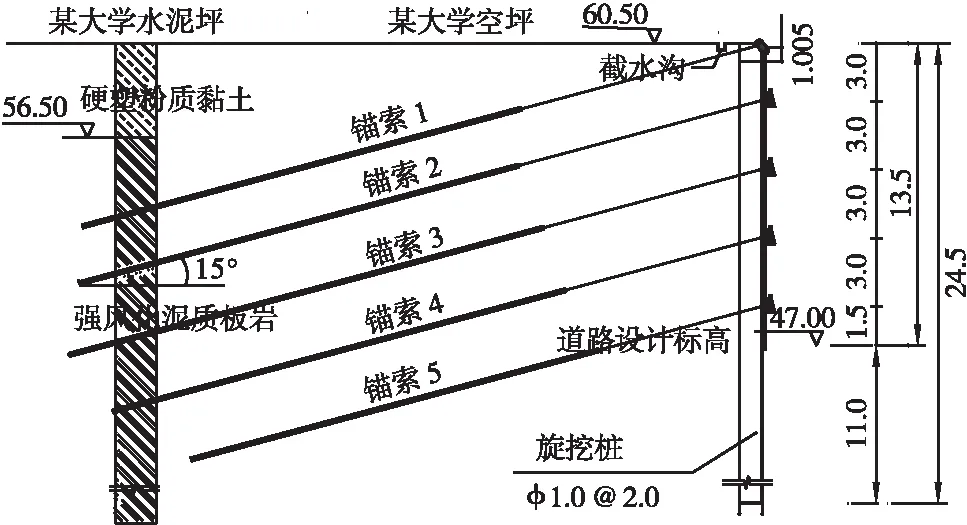
图1 K0+490～K0+525段桩锚支护剖面图(单位： m)

3 FLAC3D数值模型

3.1 模型的基本假定

1) 假定该支护结构变形满足平面问题的基本条件。

2) 假定该锚索为完全弹性体，锚索采用锚索单元。

3) 假定土体为弹塑性材料，模拟其塑性特性时屈服条件符合库伦摩尔屈服准则。

3.2 模型概况

根据工程经验以及FLAC3D数值软件的计算结果，边坡开挖影响宽度约为开挖宽度的3～4倍，影响深度约为开挖宽度的2～4倍，考虑到本边坡工程开挖深度为13.5m，故所建模型的尺寸定为85m×12m×48.5m(长×宽×高)。模型中土体采用实体单元，支护桩采用Pile结构单元，腰梁采用Beam结构单元，锚索采用Cable结构单元(一共采用5排锚杆，上3排锚杆预应力为200kN，下2排锚杆预应力为500kN)，喷射混凝土采用Liner结构单元。模型各部分位置和尺寸均按照图1建立，FLAC3D全局模型如图2所示，支护体系如图3所示。

a) 开挖前

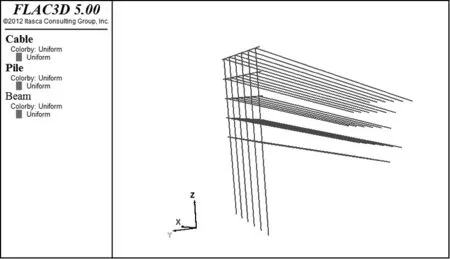
图3 模型支护系统

3.3 材料参数的选取

根据实际工程地质勘察资料和设计资料，以及查阅相关规范，确定了本模型所有材料的物理力学参数，如表1、表2所示。

表1 岩土体的特征参数情况土层名称土层厚度/m泊松比ν体积模量K/MPa剪切模量G/MPa硬塑粉质黏土40.3012.55.77强风化泥质板岩—0.2832.722.5凝聚力c/kPa内摩擦角φ/(°)抗拉强度τ/MPa重度γ/(kN·m-3)28200.018.045280.423.5

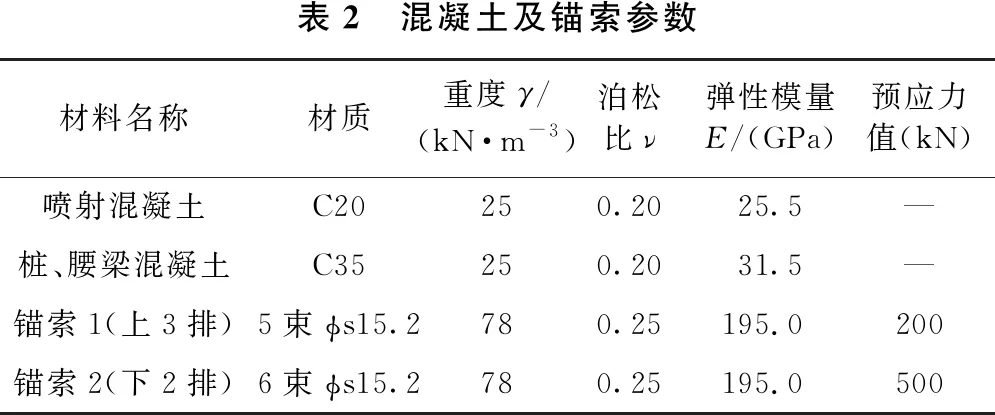
表2 混凝土及锚索参数材料名称材质重度γ/(kN·m-3)泊松比ν弹性模量E/(GPa)预应力值(kN)喷射混凝土C20250.2025.5—桩、腰梁混凝土C35250.2031.5—锚索1(上3排)5束ϕs15.2780.25195.0200锚索2(下2排)6束ϕs15.2780.25195.0500

3.4 计算工况

本模型的具体计算工况如表3所示。

表3 模拟计算工况工况边坡开挖累计深度/m支护设置11.0在0 m处设置冠梁和第1排锚杆23.5在3 m处设置第2排腰梁和第2排锚杆36.5在6 m处设置第3排腰梁和第3排锚杆49.5在9 m处设置第4排腰梁和第4排锚杆512.5在12 m处设置第5排腰梁和第5排锚杆613.5边坡开挖结束

4 排桩变形和受力模拟结果及分析

路堑式边坡的开挖是一个动态过程，边坡垂直开挖是对土体进行卸载的过程。桩锚支护结构的内侧卸去原有土压力，受到另一侧土体施加的主动土压力。坑底支护结构内侧受全部或部分被动土压力，导致边坡土体和支护结构产生相应的变形和位移[6]。

桩锚支护体系中排桩是最主要的挡土防护结构，也是桩锚支护体系设计最主要的考虑因素。因此，加强对桩锚支护结构中排桩的变形和受力研究，能更清楚地认识桩体在边坡开挖过成中的变形和受力机理，进而可为桩锚支护结构的设计和施工提供理论依据。为了更好地实现桩锚支护结构在边坡支护工程中的应用，以及更好地保证桩锚支护体系的经济型和安全性，本文从桩锚支护结构中排桩设计的控制性因素出发，主要对桩体侧向变形、桩体弯矩和桩体剪力进行分析。

本文所建模型共有6根桩，此处提取1根中间桩的数据进行分析，这样能更好的消除边界条件对计算结果的影响，使分析结果更加接近实际情况。

4.1 桩体侧向位移分析

桩体在不同工况下的侧向位移情况如图4所示，开挖完成后桩体的侧向位移云图如图5所示。图中位移值为负时代表桩体发生了朝向土体一侧的位移，位移值为正则说明桩体发生了朝向临空面一侧的位移。

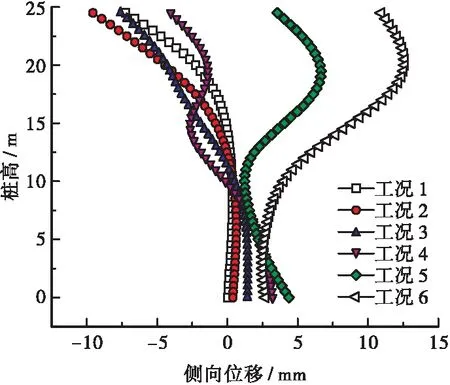
图4 不同工况下桩体侧向位移

图5 开挖完成后桩体侧向位移云图(单位： m)

由图4可知： ①工况1～4桩体发生的皆是向土体侧位移，说明桩锚结构中锚杆预应力对桩体侧向位移起到了很好的控制作用，由于所施加的预应力较大，桩体在锚杆预应力作用下不但平衡了墙后主动土压力，还产生了向土体侧位移。 ② 如工况5下位移图所示，随着开挖深度进一步加大，开挖段的桩体侧向位移由向土体一侧转向临空面。其位移最大值为6.6mm，最大值位置在距桩顶5m处，桩体侧向位移较大的部位是开挖段桩体中部，桩顶位移为3.6mm，比桩体最大位移小3mm。而开挖面以下的桩体同样向临空面一侧位移，此段桩体最大位移值在桩底端，为4.4mm。 ③ 工况6相对于工况5向下开挖了1m深度，虽然开挖深度并不大，但桩体侧向位移增加非常明显。工况6边坡开挖深度达到13.5m，此时桩体最大位移值为12.7mm，其位置在距桩顶4.5m处，位移分布形式与工况5类似，桩顶位移11mm，较工况5增大了7.4mm，增长明显。桩底位移较工况5有所减小，开挖面以下桩体位移基本接近。

由图5可知，每根桩的位移趋势基本一致，可见受边界条件影响较小。

4.2 桩体弯矩分析

桩体在不同工况下的弯矩分布如图6所示，开挖完成后桩体弯矩云图如图7所示。

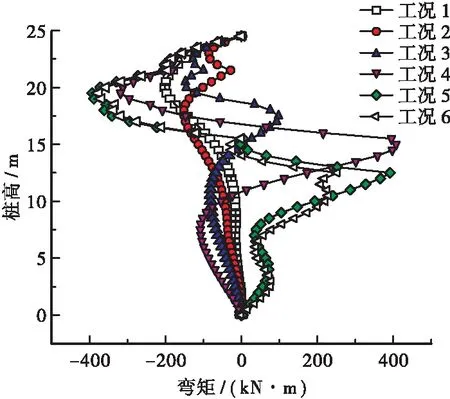
图6 不同工况下桩体弯矩分布

图7 开挖完成后桩体弯矩云图(单位： N·m)

由图6可知： ① 工况1和工况2由于开挖深度较小，弯矩比较小，且弯矩变化不大。这2个阶段弯矩值基本为负值，最大负弯矩为-201kN·m，出现在工况1阶段，而工况2由于土体开挖卸载和锚杆的一系列相互作用反而弯矩有所减小。② 随着开挖进行，桩体弯矩出现明显增加，且桩体弯矩最大值随开挖进行不断向桩体下端移动，工况3最大正弯矩为97.6kN·m，发生在距桩顶7m处，最大负弯矩为-147.5kN·m，发生在距桩顶4m处。 ③ 工况4最大正弯矩为407.1kN·m，也是整个开挖过程中桩体出现的最大正弯矩值，发生在距桩顶9.5m处，最大负弯矩为-318.4kN·m，发生在距桩顶5m处；工况4较工况3的桩体弯矩有显著增加，此段土体开挖对桩体弯矩有明显影响。 ④ 工况5相对工况4来说，最大正弯矩继续向桩体底端移动，但最大正弯矩值较工况4有所减小，而最大负弯矩值为-393.1kN·m，也是整个开挖过程中桩体出现的最大负弯矩。 ⑤ 工况6较工况5向下开挖了1m深度，但其弯矩分布曲线较工况5变化很小，仅由于开挖卸载的作用，桩体在桩高为10～12.5 m处弯矩较工况5有所减小，而其他部位变化不明显。 ⑥工况1～3的桩体在桩高为0～14m的桩段内弯矩较小，且变化较小，从工况4开始，此段桩体的弯矩有明显增加；从工况5开始，此段桩体由受负弯矩变为受正弯矩。⑦ 锚杆作用点处的桩体弯矩往往出现突变，说明预应力锚杆对桩体弯矩有很好地控制效果。

由图7可知，每根桩的弯矩云图基本一致，可见受边界条件影响较小。

4.3 桩体剪力分析

桩体在不同工况下的剪力分布如图8所示，边坡开挖完成后桩体剪力云图如图9所示。

a)

图9 开挖完成后桩体剪力云图(单位： N)

由图8可知: ① 预应力锚杆对桩体剪力影响很大，设置锚杆的位置即桩体剪力的极值点。锚杆通过施加预应力给桩体作用了一个集中力，所以该点的桩体剪力会出现突变趋势，与实际相符。 ② 随着开挖进行和锚杆的施加，下一工况都比上一工况多一个极值点。而工况6虽然没有增加锚杆，但是开挖面的土体也具有支点效果，所以工况6较工况5，在临近开挖面处多一个极值点，这与图6中弯矩的变化趋势一致。 ③ 从工况1～4，桩体剪力迅速增大，每步工况下桩体剪力绝对值的最大值都发生在新增锚杆的位置。且整个施工过程中的剪力最大值出现在工况4中，这与弯矩最大值出现在工况4一致，该剪力最大值为360kN，位置在距桩顶9m处，位于第4排锚杆上方0.5m处。 ④ 工况5较工况4剪力最大值有所减小，工况5剪力最大值258kN，与工况4的剪力最大值处于同一位置。工况6较工况5除了在开挖面附近新增一个极值点外，其他部位的剪力较工况5略微有所减小。⑤ 桩高10m以下的这段桩体，工况1～3剪力非常小，这主要是工况1～3开挖深度较小，此段桩体几乎还没发生什么变形，这与图4中桩体侧向位移的结果相符。随开挖进行，从工况4到工况6，此段桩体剪力有明显增加。但此段桩体埋在土中，变形较小，所以其剪力值较上部桩体小得多，最大值不超过100kN。

同样由图9可知，每根桩的剪力云图基本一致，再一次证明了数值计算结构受边界条件影响小。

5 结论

综上所述，可得出以下几点结论：

1) 预应力锚杆对排桩的侧移有明显的约束作用。当锚杆预应力较大、边坡开挖深度较小时，排桩的侧向位移很小，甚至会由于锚杆的作用而发生朝向土体一侧的位移。但随着边坡开挖深度增加，排桩朝向临空面的侧移将明显增大。在本工程实例中，桩体最大侧移为12.7mm，此时的开挖深度为13.5m。

2) 预应力锚杆以集中力的形式作用于桩体上，不仅对桩体变形有很好的控制作用，对桩体弯矩和剪力也有很好的控制作用，避免了类似悬臂桩出现剪力和弯矩很大的情况，桩锚支护结构的安全性更好。在本工程实例中出现的剪力最大值为360 kN，弯矩最大值为401.7 kN，2者均发生在工况4。

3) 研究结论与文献[1]～[10]中所得结论相比，虽然因工程实际条件不同而在数据上有差别，但整体变化规律和趋势基本一致，说明本文建模方法正确、所得数据正确、结论可靠。