一种基于离散余弦变换的嵌入式图像编码算法

陈鑫，游敏娟，崔艺君，张勇，王世刚

1.山东第一医科大学（山东省医学科学院）放射学院，山东泰安271016；2.山东医药技师学院，山东泰安271016

前言

图像数据文件通常包含着大量的冗余信息，这为数据压缩提供了可能。随着小波变换、分形几何等数学理论的深入发展，相继出现小波变换编码［1-4］以及与分形编码［5-7］结合的新颖高效的现代编码方法［8-9］。小波变换图像编码算法中，小波基的选择密切关系到压缩算法的性能。如果小波基函数与图像原信号越相似，则能用越少的求和项来逼近原信号，压缩性能就越好。因此，在小波压缩算法中，小波基直接影响着压缩效果，选择一个合适的小波基就显得尤为重要。

本文提出一种基于离散余弦变换的图像嵌入式编码算法，它不像小波压缩算法那样面临选择最优小波基的的困扰，任何图像离散余弦变换仅需要同样的变换核。本文设计的基于离散余弦的图像嵌入式编码算法，能够根据目标码率或失真度大小要求随时结束编码，并能解码近似恢复原图像。结果证明，该算法是一种十分高效的图像编码算法。

1 原理

1.1 嵌入式编码理论

嵌入式编码（embedded coding）就是编码器将待编码的比特流按重要性的不同进行排序，根据目标码率或失真度大小要求随时结束编码；同样，对于给定码流解码器也能随时结束解码，并可以得到相应码流阶段处的目标码率的恢复图像。

嵌入式编码中首先传输的是最重要的信息，其次是次要的信息。嵌入式编码中数据排序算法的优劣和排序信息的处理决定了整个编码算法的效果。著名的嵌入式零树小波编码算法是目前为止最为有效的小波编码算法之一，并且出现了很多零树小波编码的改进算法并应用图像编码［10-14］。

1.2 图像离散余弦变换（Discrete Cosine Transform,DCT）

图像的DCT 属于正交变换，变换后的图像的能量不变，并且能量变得集中：即将整幅图的能量集中在低频部分，位于变换域的左上角区域，而高频能量集中在右下角区域。因此，可以利用图像余弦变换域数据集中的特点实现图像的压缩［15］，也可以实现图像的增强、降噪及其他应用［16-20］。图像的二维离散余弦正、逆变换公式见式（1）和式（2）：

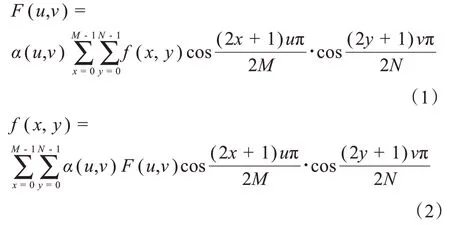
其中，α(u) =

正变换x= 0, 1, 2,…,M- 1;y= 0, 1, 2,…,N- 1。

反变换u= 0, 1, 2,…,M- 1;v= 0, 1, 2,…,N- 1。

1.3 本文编码算法

本文提出的嵌入式图像余弦变换编码算法是变换编码的一种，由3 个基本部分组成：变换、扫描、量化。

（1）变换。首先是原始图像数据通过离散余弦变换后产生变换域系数，由于正交变换并不改变图像的能量，变换这一步骤并不能压缩图像，但是能量在变换域变得集中。

（2）扫描。该步骤是图像编码的关键，为实现在任意时刻结束并提高数据的“最好”表示，需对变换的余弦系数按其重要性进行排序。这样，必须先扫描代表图像重要信息的低频变换域系数，再扫描高频变换域系数。由于图像变换后含有重要信息的系数在变换域左上角区域，所以需要先扫描左上角的系数。

图1所示扫描方式可以很好的编码系数的空间位置信息和扫描过程，系数坐标用（i，j）表示，其中i表示行数，j表示列数。在每一个扫描步长（A）的情况下，先进行行扫描，即从第一行扫描至步长（A）行；再从第一列扫描至步长-1（A-1）列；然后增加步长为（A+1），重复以上步骤，先进行行扫描，即从第一行扫描至步长（A+1）行，再从第一列扫描至步长-1（A）列；然后增加步长为A+2，重复以上扫描步骤。并且根据目标码率或失真度大小要求所确定的数据量随时结束编码。

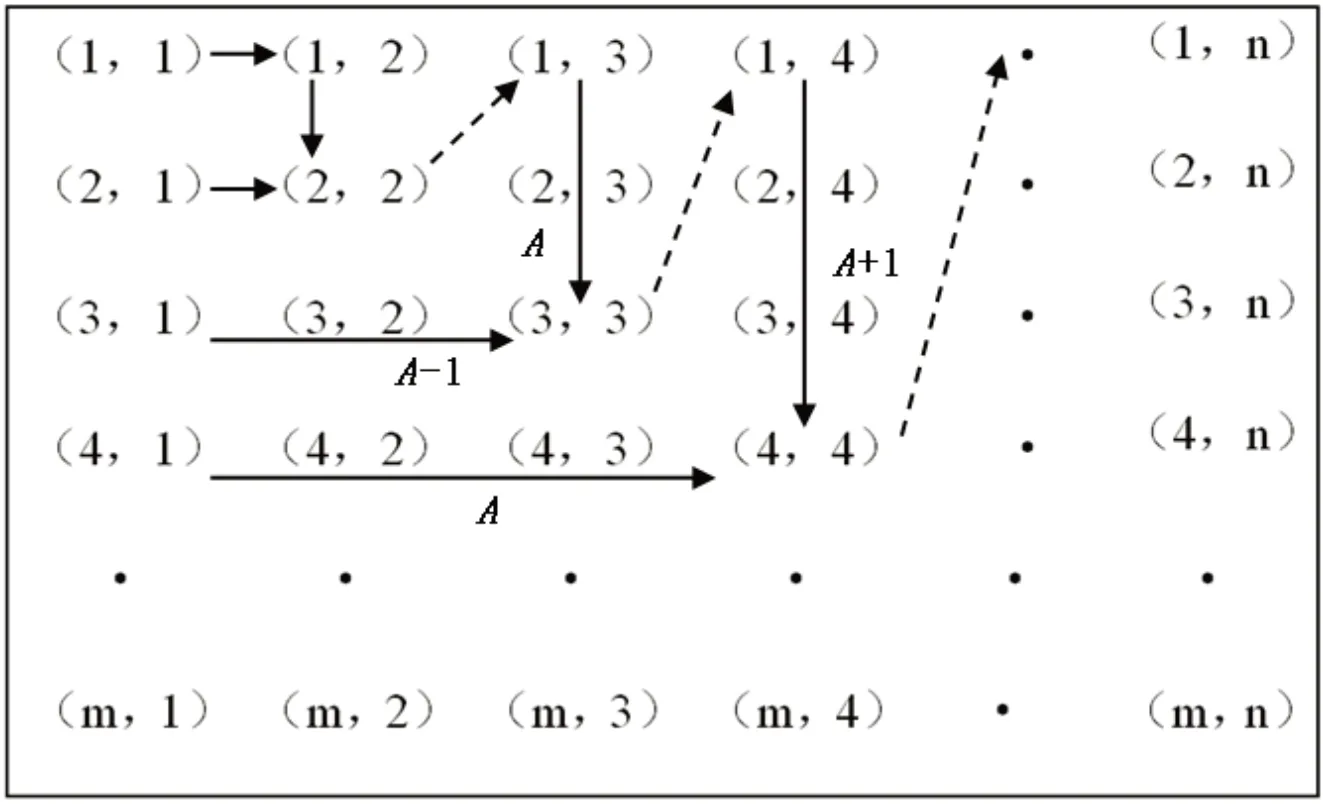
图1 扫描过程Fig.1 Scanning process

这样，按上述扫描步骤扫描数据的顺序为（1，1）→（1，2）→（2，2）→（2，1）→（1，3）→（2，3）→（3，3）→（3，1）→（3，2）→（1，4）→（2，4）→（3，4）→（4，4）→（4，1）→（4，2）→（4，3）→（5，1）→（5，2）→…

（3）量化。该步骤要对扫描后的系数进行量化传输，因为一般图像经DCT 后低频系数数值可达104，且随着图像内容和位深的不同，有的甚至更大，若用较少的编码位数表示变换域余弦系数，则必须进行量化。

对变换域数据进行量化，选出传递系数的最小值Xmin与最大值Xmax，若编码为每个系数用Nbits 表示，因为系数有正有负，所以符号占用1 bit，系数绝对值映射到［0,2N-1-1］，公式为：

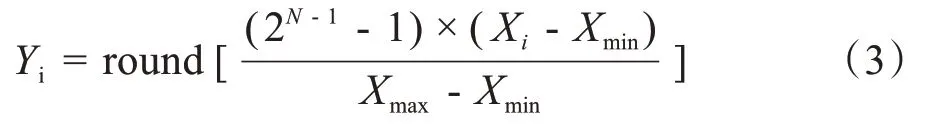
其中，Xi为余弦变换系数，Yi表示系数Xi的量化值，round( )表示四舍五入。

解码过程是编码过程的逆过程，解码时系数的绝对值是式（3）的逆运算，公式为：

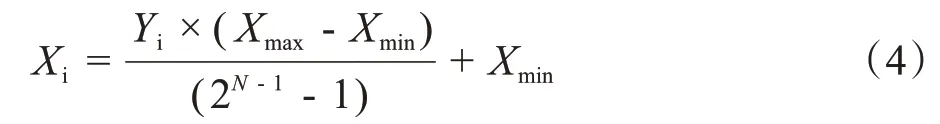
2 方法

本文对一幅掌骨CR 图像进行DCT，然后对变换域余弦系数进行扫描量化编码，并计算其客观指标，其步骤如下：

（1）对CR 图像进行DCT，得到变换域余弦系数。（2）对余弦系数进行本文算法扫描。（3）扫描后按公式（3）进行量化传输。（4）解码过程是编码过程的逆过程。将接收的数据按公式（4）进行反量化得到余弦系数，再进行余弦反变换近似恢复原图像。（5）评价恢复图像采用均方根误差（Root Mean Square Error, RMSE）和峰值信噪比（Peak Signal Noise Ratio,PSNR）：

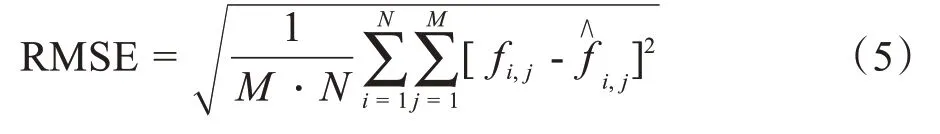
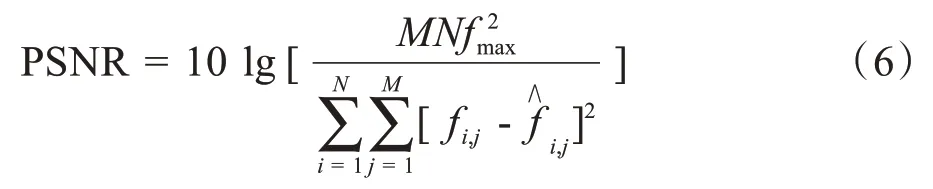
3 结果

表1显示CR 图像编码客观指标RMSE 与PSNR随着压缩比变化的情况。CR 图像DCT 嵌入式编码结果见图2。

从表1和图2可以看出，本文提出的基于离散余弦变换的嵌入式图像编码算法，能够随时结束编码，在足够数据量的情况下可获得较好的视觉效果。且随着压缩比的减小，即传输数据量的增加，无论是主观质量还是客观指标RMSE与PSNR都有较大改善。

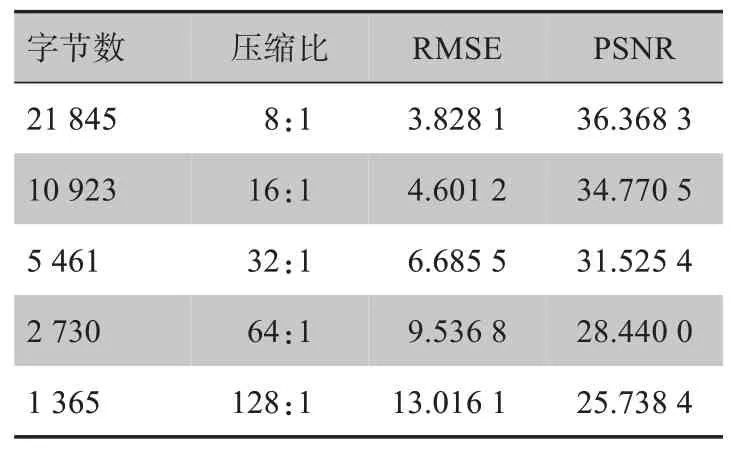
表1 图像编码客观指标Tab.1 Objective indicators of image encoding

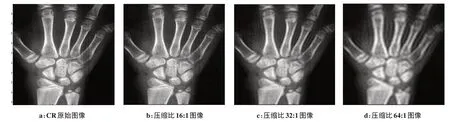
图2 图像编码结果Fig.2 Image encoding results

需要指出的是变换域系数的量化位数影响着解码图像质量，量化位数越大，反量化时恢复的数据与原余弦系数数据误差越小，编码效果较好。本文采用量化位数为12位，其中符号占1位，数据占11位。

4 结论

图像余弦变换具有良好的频率域局部化特性，是图像分析最有效的工具之一，被广泛应用于图像处理的去噪、增强、编码等各个方面。本文提出一种基于DCT 的图像嵌入式编码算法，任何图像变换需要的是同样的变换核，避免了小波变换编码面临选择最优小波基的困扰；并且能够根据目标码率或失真度大小要求随时结束编码，并能解码实现原图像。本文的研究结果对于图像正交变换编码具有一定的实际意义。