“大单元整体教学”视野下的教学结构分析——以《认识比》为例

■广东省江门市蓬江区教师发展中心 黄肖慧

小学数学大单元整体教学，就是审视数学教材的自然单元，将有内在知识联系的单元内容构成整体，并且根据学生的认知规律，组织系统化、科学化的课堂教学。教学结构分析作为单元整体教学中的重要因素之一，直接影响教学过程的实施与学生认知结构的形成。那么，如何开展单元整体教学结构分析呢？经过梳理和提炼，我以为，主要从单元各例题之间的教学路径、单元内容在不同学段的起源与发展、认知基础与知识结构融通三个维度展开研究。下面以人教版六年级上册《认识比》为例展开阐述。

一、明晰单元各例题之间的教学路径

在《认识比》单元中，“比”无疑是单元核心概念。从实验版教材“两个数相除又叫作两个数的比”到修订版教材“两个数的比表示两个数相除”，可见“两个数相除”与“两个数的比”既有联系，又有区别。有自身的特点、意义和价值，修订版教材更加强调两个量之间的“倍比关系”。

解读例题，了解单元内容各例题之间的教学路径，是一种解构行为。解读过程中，要思考以下问题：单元的核心内容、核心概念是什么？本单元一共有多少个例题？各例题之间有怎样的教学关系？例题的问题情境想表达什么？建构以核心概念为中心的逻辑结构，分析教材中例题之间的联系及教学目标，有利于教师整体规划课时，制定具有联系、结构化的教学目标。

二、理清单元内容在不同学段的起源与发展

审视与研读知识在单元、年级、学段的分布，意在了解整个小学阶段“比”相关内容的呈现序列，梳理知识之间的起源与发展。下面以人教版数学教材“比”及其相关知识学习为例，说明其在不同学段的起源与发展（见表1）。

（一）起：“比”起源于除法与“倍”

两个数的比表示两个数相除。追溯到二年级下册“除法的初步认识”，除法意义中的“包含除”，表示的就是两个数的比，如把8条红金鱼每2条放在一个鱼缸里，需要几个鱼缸？这正是两个同类量的比的原型。“比”既表示同类量的比，又表示不同类量的比。其中，同类量的比和“倍”有着密切的关系。例如鸡有10只，鸭子有15只，可以用15÷10表示鸭子数量是鸡的多少倍，也可以用“15比10”表示鸭子数量与鸡的只数比；可以用10÷15表示鸡的只数是鸭子的几分之几，也可以表示鸡的只数与鸭子只数的比是“10比15”。可见，“比”起源于除法与“倍”。

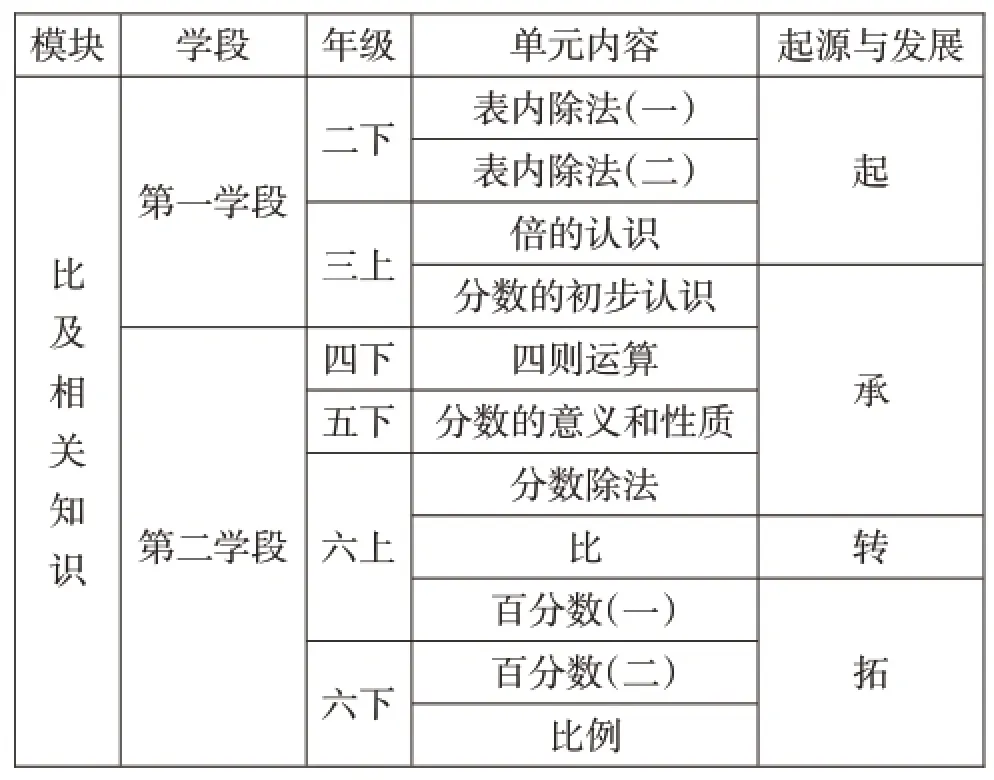
表1“比”及相关知识的起源发展

（二）承：分数相关知识是“比”的重要承托

从《分数的初步认识》到《分数的意义》再到《分数除法》，通过两年的学习，学生逐步理解了分数意义和性质，也能联系分数的含义解答求一个数是另一个数的几分之几等实际问题，这些都是学生理解比的知识的重要承托。通过分数相关知识的学习，有助于学生沟通分数、除法与比的联系，丰富和加深对分数和除法的理解，进一步提高分析和解决实际问题的能力。

（三）转：迁移转化是学习“比”的关键

“比”借助除法之势，由“倍”导入，通过迁移转化为两个同类量的比，进一步推广至不同类量之比。但是“两个数相除”与“两个量的比”并不等价，表现为：一是除法中包含除有“比”的内涵（两个同类量的比），而均分除只指向一个量，不含有“比”的内涵；二是“比”是两个变量之间的不变关系，重点表现一种状态，而除法是一种运算，趋向运算的形式和结果，“比”只有求比值时才利用除法进行运算；三是“比”与除法均源于度量，如长度、面积、时间等都可度量，量与度量单位的度量结果表现为“比值”或“商”，同时，“比”还可以表示浓度、颜色、质地等不可度量的比，即两个不同类量的比。

（四）拓：《百分数》与《比例》是《比》的拓展与深化

“比”可以扩展为变量之间的正比例函数关系，而《百分数》的学习，又使除法、分数、比、百分数、比例形成了紧密的关系网，让我们看清了“比”的前世今生。

三、实现认知基础与知识结构的融通

小学数学单元整体教学结构分析，既要重视数学知识结构（客体）的分析，更要重视学生认知基础（主体）的分析，并通过对数学知识结构与学生认知基础的融通分析，使教学主体、客体达成对立统一的平衡。要了解学生的认知基础，不能仅仅依靠过往教学经验，需要一定的调研。

以《认识比》为例，我们采用了访谈的方式对40位六年级学生进行前测。测试结果显示，约68%的学生能列举“比”的例子，24%的学生列举了体育赛事的比分，还有约8%的学生把“比”与“比例”混为一谈。只有15%的学生能用“倍比”解决问题，约有20%的学生用差比关系解决问题，37%的学生无法解决问题。只有5%的学生能联系“倍比”“相除”关系解释“比”。

以上测试数据反映，学生对“比”的认识绝大多数停留在生活层面，对“比”的意义缺乏本质的认知。教学中，教师应摒弃过去对“比”概念的字面形式解读，着力解决两个问题：1.引导学生理解“两个数相除”与“两个数的比”之间的区别与联系；2.体会为什么要学习“比”，体会“比”的本质与价值。在这一过程中，从“除法—份数—分数”大单元关系结构中，突出“每一份相等”“份数对等”的关系尤为重要。