具有时滞和脉冲捕获、污染物脉冲输入的捕食-食饵-环境模型
2021-01-09章培军
章培军, 王 震, 陈 恒
(西京学院理学院,西安 710123)
1 引言
害虫爆发常常会引发严重的经济和生态问题,我国作为一个农业大国,害虫治理问题一直是关注的热点,如何有效地控制害虫也是大家最关心的问题.人们采取了各种措施控制害虫的爆发,如化学控制(喷洒农药)和生物控制(脉冲投放天敌)等,农业部门和研究学者们提出了害虫综合控制策略,要求合理有效地使用这两种控制手段.
捕食-食饵模型是种群动力学中重要的模型,也是生态学与生物数学的一个重要研究课题,很多学者研究了影响捕食-食饵模型动态特性的因素,如功能反应、时滞、阶段结构和收获等,特别是这些因素的共同作用[1-4].然而,种群动力学中有许多自然现象和人为干预因素的作用都可以用脉冲微分方程来刻画,脉冲效应在生态学系统中描述某些运动状态的快速变化和跳跃,如生物种群个体的出生、人类对生物资源的脉冲捕获与投放等[5-8],它能更真实地反映自然界的发展过程.
随着工业、农业的快速发展,环境污染日益严重,研究环境中污染物或毒素对种群乃至生态系统的影响成为生态数学的热点问题,早在20 世纪80 年代,Hallam 等[9-11]假设种群的增长率线性依赖于对毒素的吸收,研究了这种毒素排放到环境中对生物种群的影响,揭开了此方面的研究序幕.后来,很多学者在此领域进行了大量的工作,取得了很多研究成果[12-16].其中,李冬梅等[14]研究污染环境下脉冲输入毒素对具有阶段结构的单种群的影响,得到了种群灭绝和持久生存的充分条件,为控制环境中毒素对种群生长的影响提供了理论依据.然而,在实际生态系统中,几乎没有独立的单种群存在,而是多种群共同存在,故考虑捕食-食饵关系的两种群生态模型更符合实际.并且在污染的环境中,有些天敌受污染物或毒素的影响,使其数量减少,甚至灭绝,这使得我们需要控制污染物排放的数量和周期,保证天敌种群可以持续生存.另一方面,农药喷洒过多,会使害虫大量减少,但同时也对环境造成了严重的污染,在毒杀害虫的同时,也杀害了天敌.为了保持生态平衡,不需要使害虫完全灭绝,当害虫不会带来非常大的经济损失时,我们希望害虫和天敌能够持续生存.
2 模型的建立及预备知识
综上所述,本文研究脉冲污染的环境中,捕食者具有阶段结构、食饵具有脉冲收获的时滞捕食-食饵-环境模型的动力学性质,包括捕食者灭绝周期解的全局吸引性和系统持久性,考虑如下模型
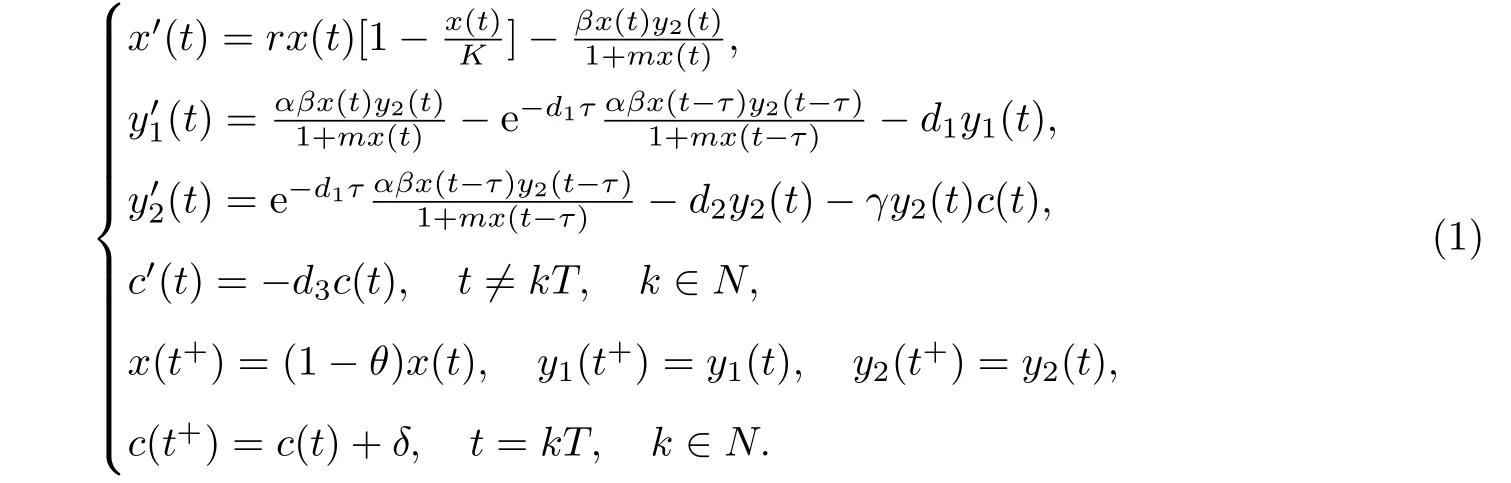

由于系统(1)的第一、三、四方程都不显含y1(t),所以考虑系统
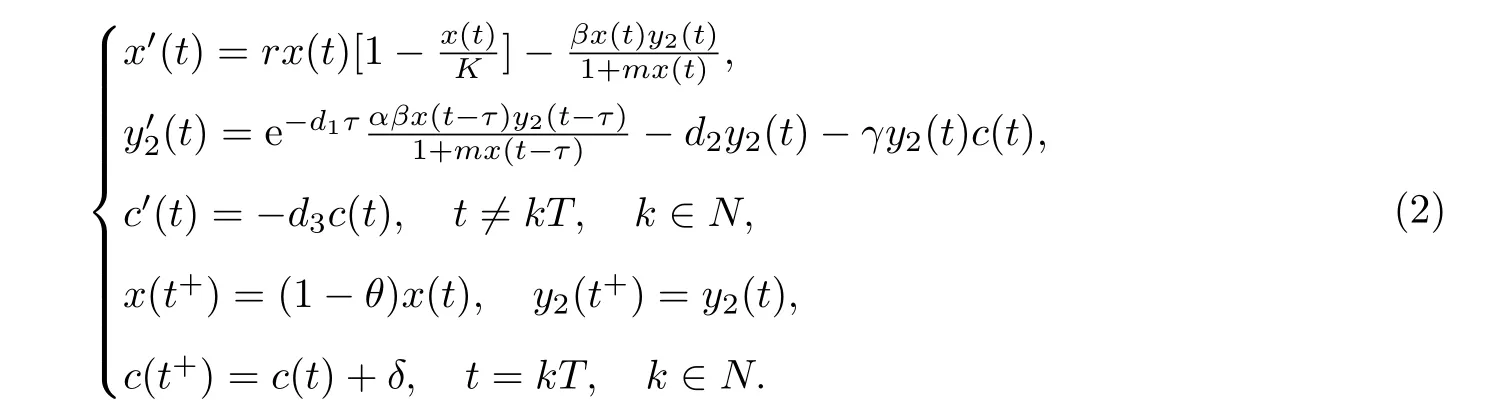
系统(2)的初始条件是
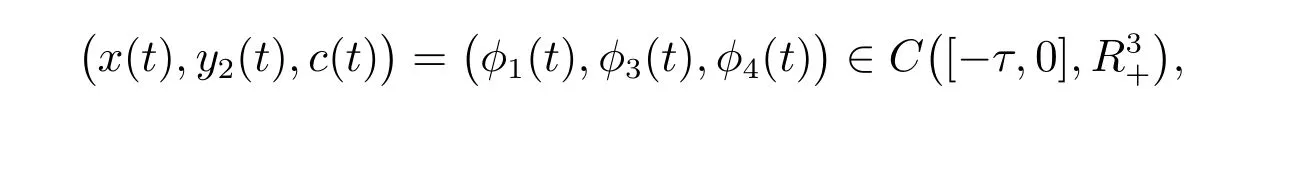
且在−kT(k ∈N)处不连续,而是左连续,即
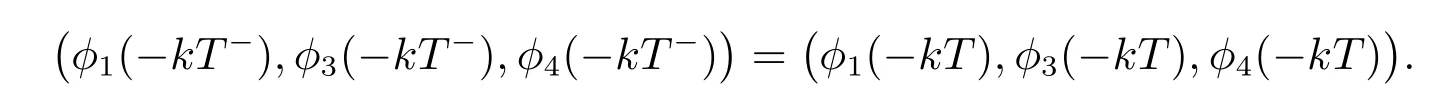
考虑到系统的生物意义,我们假设φ1(0)>0, φ3(0)>0, φ4(0)>0.
引理1[17]对于系统(1)的所有解,当t 足够大时,存在一个常数Q>0,使得x(t)≤
Q, y1(t)≤Q, y2(t)≤Q, c(t)≤Q.
引理2[5]考虑脉冲系统
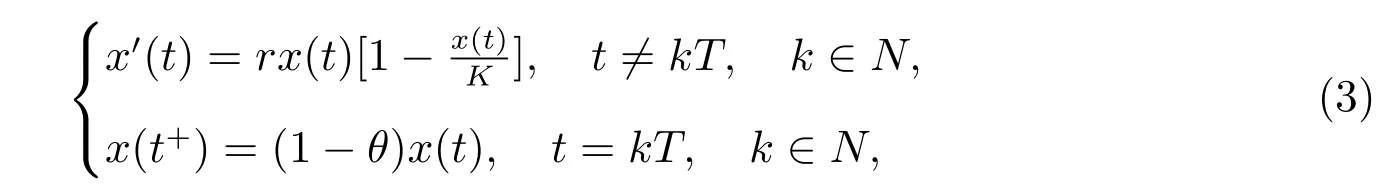
其中r >0, K >0, 0<θ <1,则系统(3)存在唯一正周期解
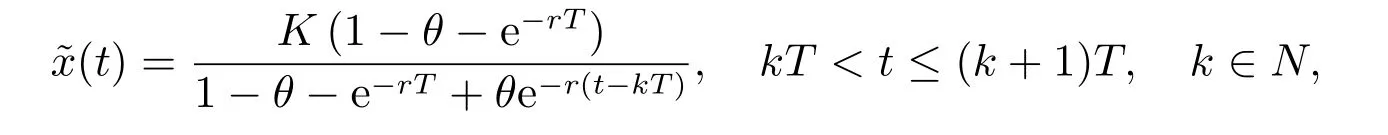
且全局渐近稳定.
引理3[15]考虑脉冲系统

其中d3>0, δ >0,则系统(4)存在唯一正周期解

且全局渐近稳定.
引理4[18]考虑下列微分方程
x′(t)=ax(t −τ)−bx(t),
其中a, b, τ >0,当−τ ≤t ≤0 时,x(t)>0,则:
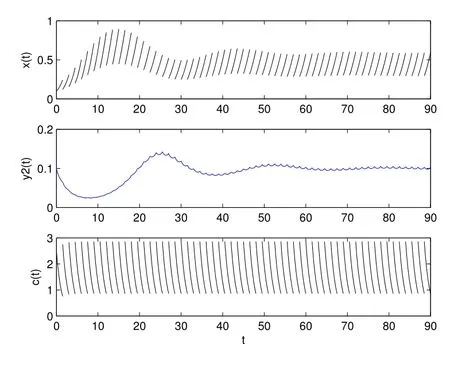
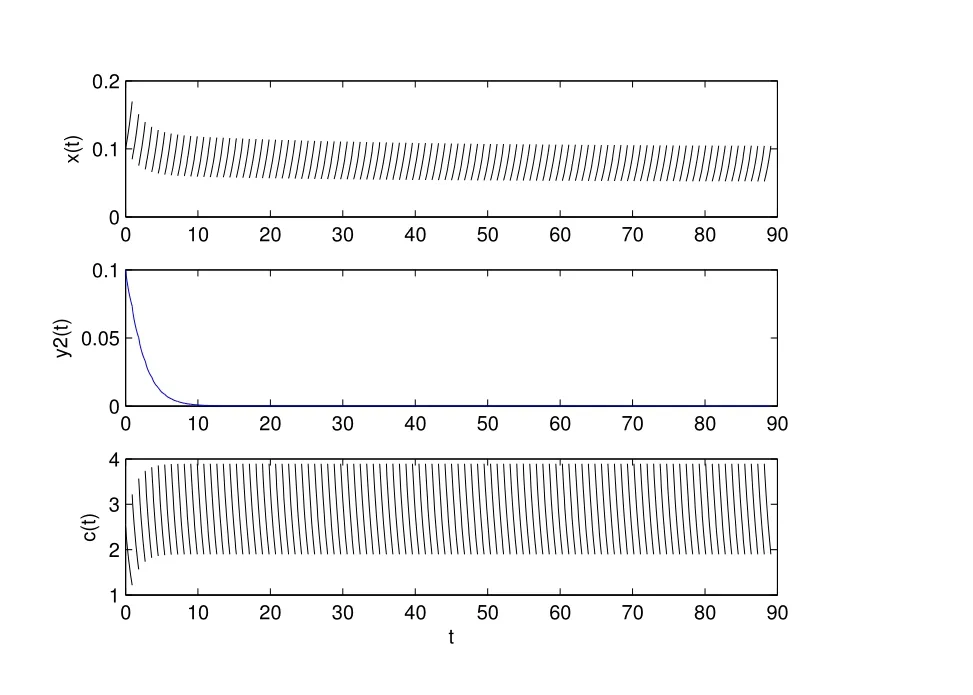
1) 如果a 2) 如果a>b,则limt→∞x(t)=∞. 在系统(2)中,令y2(t)=0, t ≥−τ,则可得到如下系统 由引理2、3,得到系统(5)的周期解为 且全局渐渐稳定. 定理1 如果R1< 1 时,则系统(2)的捕食者灭绝周期解((t),0,(t))是全局吸引的,其中 证明 由于R1<1,选择充分小的ε0, ε1>0,使 从系统(2)的第一个方程,得到 考虑带有脉冲的比较系统 由引理2,得到系统的周期解为 由比较原理[19],存在n1∈N 和任意小的整数ε0,对任意t>n1T,满足 即 从系统(2)的第二个方程,得 考虑如下的比较系统 由引理4,得到limt→∞y(t)=0,因此,limt→∞y2(t)=0,对充分小的ε2> 0,存在整数n2>n1,任意t>n2T,有y2(t)<ε2. 对任意t>n2T,由系统(2)的第一个方程,得到 考虑带有脉冲的比较系统 由引理2,得到系统的周期解 由比较原理,则存在整数n3>n2,使得对任意t>n3T,满足 由于ε0与ε2充分小,得到 是全局吸引的,又由引理3 知,当t →∞时,c(t) →(t),从而系统(2)的捕食者灭绝周期解((t),0,(t))是全局吸引的. 推论1 如果θ =0 且τ >τ∗1或δ >δ∗,则系统(2)的捕食者灭绝周期解((t),0,(t))是全局吸引的,其中 推论2 如果δ =0 且τ >τ∗2或θ >θ∗,则系统(2)的捕食者灭绝周期解((t),0,(t))是全局吸引的,其中 定理2 如果R2> 1 且t 足够大时,则存在正常数M,使得系统(2)的每一个正解(x(t),y2(t),c(t))都满足y2(t)≥M,其中 证明 系统(2)的第二个方程,可写成 定义 由系统(2),得到F(t)的导数 考虑带有脉冲的比较系统 得到系统的周期解为 其中 根据脉冲微分方程的比较原理,则存在t1(t1> t0+ τ)和充分小的ε > 0,使得t>t1时,x(t)≥2(t)−ε,从而 由式(6)和(7)可知,对所有的t>t1,有 根据定理2 和以上讨论,我们不难得出:当R2>1 时,系统(1)是持久的. 本文建立了一个在污染环境中,捕食者具有阶段结构、食饵具有脉冲收获的时滞捕食-食饵模型,并且污染物被脉冲地输入到环境中,导致捕食者的数量减少.为了得到捕食者灭绝周期解的全局吸引性和系统持久性的充分条件,定义了两个阈值R1和R2,当1 −θ −e−rT>0 时,明显有R1>R2. 当R1< 1 时,由定理1 可知,系统的捕食者灭绝周期解是全局吸引的,捕食者在一段时间后灭亡,食饵种群及污染物的浓度呈周期波动. 当R2>1 时,由定理3 可知,系统是持久的,种群是持续生存的. 当R2< 1 < R1时,系统(2)的动力学性态会发生改变,例如,取r = 0.8, K =2, β =1, m=0.5, α=0.8, d1=0.3, d2=0.4, γ =0.1, d3=0.8, θ =0.5, δ =2, τ =0.5, T =1.5,经计算得到R1=1.0272, R2=0.4445,有R2<1 图1 捕食者灭绝 图2 系统是持续的 根据定理1 和3 可知,种群能否持续生存,主要依赖于食饵的捕获率θ,污染物的脉冲输入量δ 和脉冲作用的周期T.如果食饵的捕获率θ、污染物的脉冲输入量δ 过大,或者脉冲作用的周期T 过小,捕食者是灭绝的.选择参数值r = 0.8, K = 2, β = 2, m =0.5, α=1.2, d1=0.3, d2=0.4, γ =0.1, d3=0.8, θ =0.5, δ =2, τ =0.5, T =1.5,经计算得到R2= 1.3335 > 1,由定理3 可知系统是持续生存的,如图3 所示.在其它参数不变的情况下,当增加食饵的捕获率至θ = 0.68 时,R1= 0.6592 < 1,由定理1 可知捕食者灭绝,如图4 所示;当增加污染物的脉冲输入量至δ = 30 时,R1= 0.8849 < 1,由定理1 可知捕食者也灭绝,如图5 所示;当减少脉冲作用的周期至T = 0.9 时,R1=0.3439 < 1,由定理1 可知捕食者还是灭绝的,如图6 所示.为了保持系统的持续生存,我们应该控制污染物输入的周期和数量,同样也要合理控制食饵的捕获.这些为我们今后对生物资源的开发、种群数量的收获及环境的控制提供了宝贵的理论依据. 图3 系统是持续的 图4 增加食饵的捕获率至0.68 时,捕食者灭绝 图6 减少脉冲作用的周期至0.9 时,捕食者灭绝3 捕食者灭绝周期解的全局吸引性
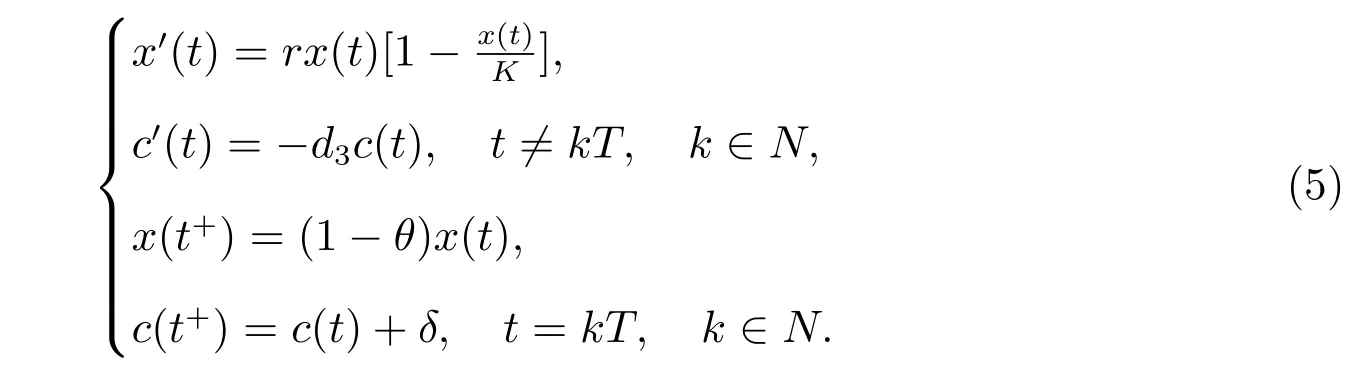
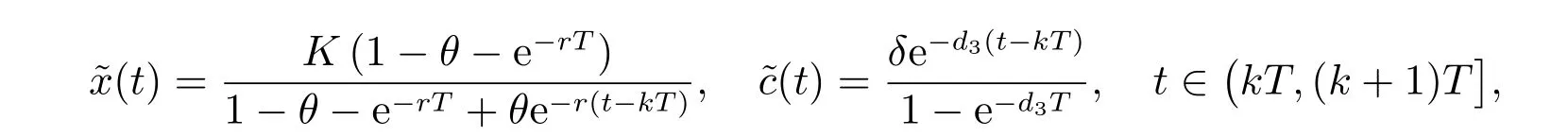
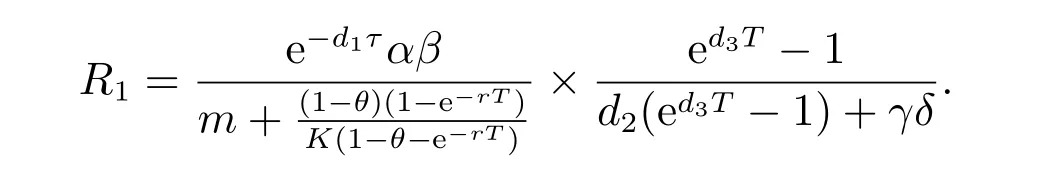
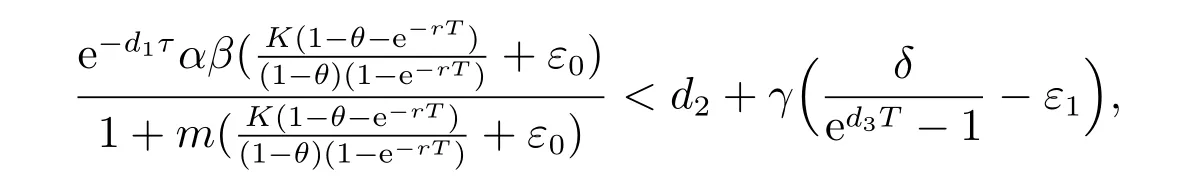
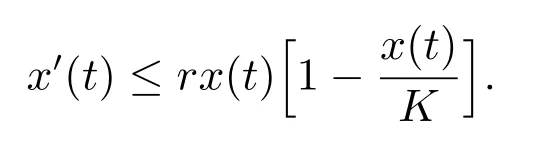


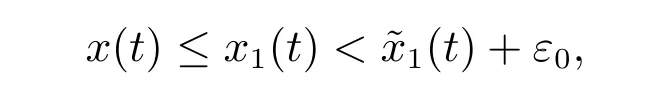
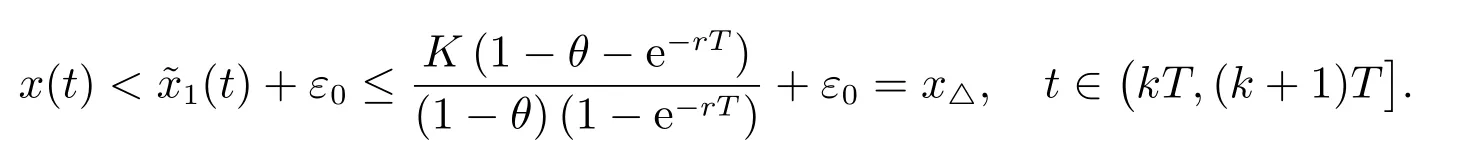
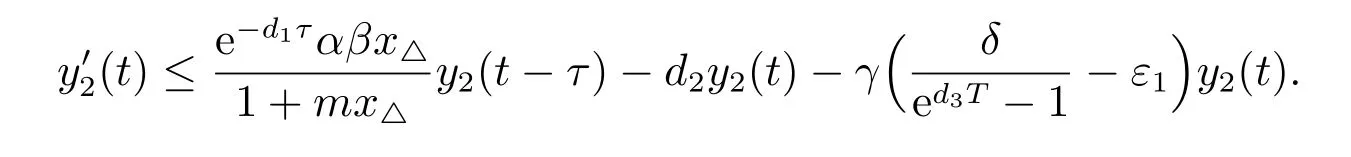






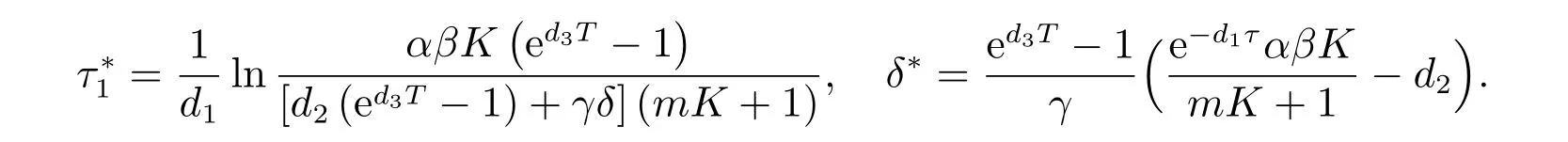
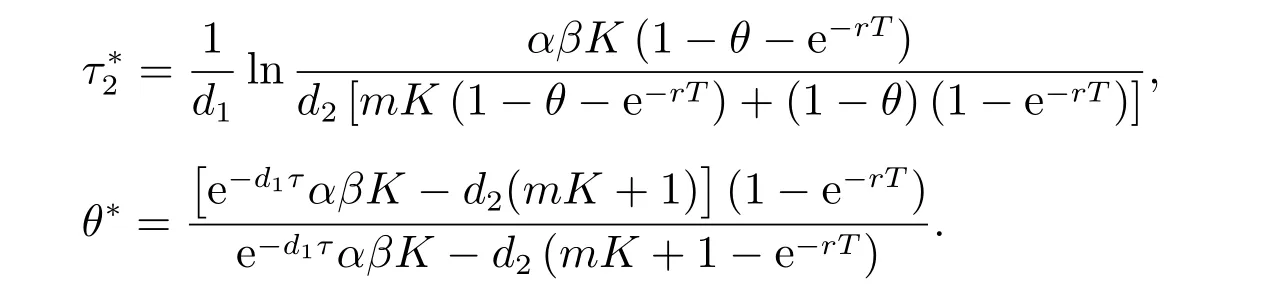
4 持久性

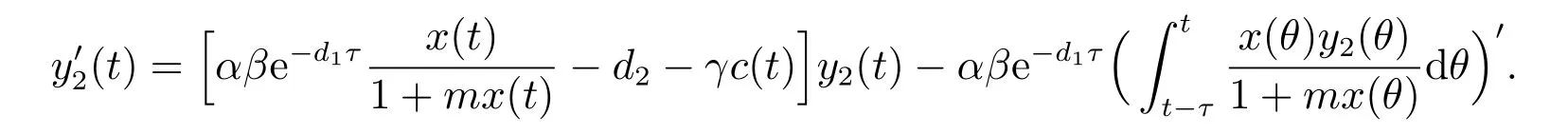







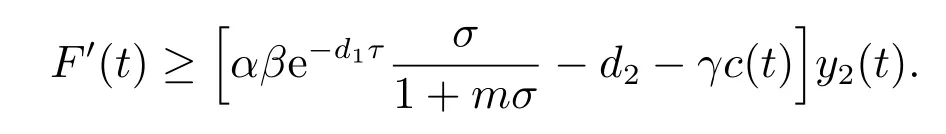


5 结论与数值仿真