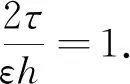变系数Cattaneo方程的有限差分法
2021-01-09毕彦明
毕彦明 尹 哲
( 山东师范大学数学与统计学院,250358,济南 )
1 引 言
传统的Fourier定律和Fick定律广泛并成功地应用于研究热传导和扩散问题中.由于这两个定律均不涉及时间项,其中就隐含了无限的传播速度.严格来说,这是非物理的研究领域.Cattaneo模型[1]提供了一个以有限传播速度为特征的热传导模型.Ghazizadeh等人[2]给出了分数阶Cattaneo方程的显式和隐式有限差分算法,在对显式差分格式进行稳定性分析的时候引入了CFL数,并证明了该格式的稳定性条件.黄雅婷等人[3]给出了Cattaneo方程的四阶紧致差分格式.然而,一些研究表明,在某些实际应用中扩散系数会随着空间或时间变化,例如,在由不同热传导性质材料组成的混合材料的热传导问题中,扩散系数会随着空间的变化而变化,并满足如下的Cattaneo方程
(1)
其中Ω:={(x,t)∈R2:0≤x≤L,0 变系数方程常用于描述一些与非均匀介质相关的传播过程,如声波在非均匀无损流体介质中的传播[4],非均匀介电常数介质中电偶极子的原子发射率[5],非均匀介质中外周期势对Levy飞行的影响[6]等.R Ciegis[7]提出了数值求解双曲型导热问题,其中导热系数与时间相关,构造并研究了显式和隐式欧拉格式,为了使隐式欧拉格式规则化,提出了一种简单的时间步长和空间步长之间的线性关系,自动引入数值粘性,并给出了数值实验结果.赵璇等人[8,9]给出了带有可变扩散系数的分数阶扩散方程的一个紧致有限差分格式和一个box-type有限差分格式,并给出了分数阶变系数Cattaneo方程的紧致C-N格式. 李晓丽等人[10]介绍了分数阶Cattaneo方程的块中心有限差分法,其扩散系数也是与时间相关的,并证明了该方法的无条件稳定性和全局收敛性.在非均匀介质中,扩散系数在空间变化,假设D(x)足够光滑且满足0 在点(xi,tk)处,由泰勒展开式得 (2) (3) (4) (5) 由(4)式和(5)式相减并除以h,得 (6) 其中Rik=O(τ2+h2). 整理可得显式差分格式为 (7) 2.2隐式差分格式下面,提出一种无条件稳定的隐式差分格式.用第k+1层和第k-1层去逼近空间变系数项,令 (8) 结合(2)式、(3)式、(6)式和(8)式可得 整理得到隐式差分格式为 (9) 该隐式差分格式是无条件稳定的,其截断误差为O(τ2+h2). 算例1令方程(1)中ε=0.1,D(x)=x2+1,u0(x)=sinπx,u1(x)=0, 精确解u(x,t)=t3sinπx,其中源项为 f(x)=6ε2tsinπx+3t2sinπx+π2t3sinπx(x2+1)-2xπt3cosπx, 应用差分格式(7)和(9)求解上述问题. 表1 显式格式L2误差 表2 隐式格式L2误差 由表1和表2可以看出,显式格式和隐式格式都是关于空间与时间2阶收敛的.2 格式建立
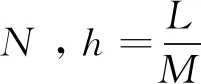
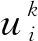

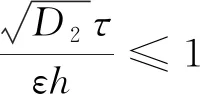
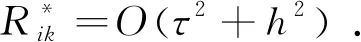
3 数值模拟