非线性Klein-Gordon-Schrödinger(KGS)方程的数值解法

杨玉娜 李宏伟

( 山东师范大学数学与统计学院，250358，济南 )

1 引 言

本文考虑如下非线性Klein-Gordon-Schrödinger(KGS)方程[1]的数值解法：

i∂tψ+Δψ+λ|ψ|p-1ψ+uψ=0,x∈[xl,xr],t∈(0,T],

(1)

∂ttu-Δu+u-|ψ|2=0,x∈[xl,xr],t∈(0,T],

(2)

其初边值条件为

ψ(x,0)=ψ0(x),u(x,0)=u0(x),∂tu(x,0)=u1(x),x∈[xl,xr],

(3)

ψ(xl,t)=ψ(xr,t)=0,u(xl,t)=u(xr,t)=0,t∈(0,T].

(4)

方程(1)-(4)描述了复中子场和实标量介子场之间的相互作用，其中ψ(x,t)是复值函数,u(x,t)是实值函数, 且i2=-1,p>1,λ是实数.

方程(1)-(4)描述的问题满足如下质量守恒定律(5)与能量守恒定律(6):

(5)

ε(t)≡ε(0)

(6)

众所周知, 薛定谔方程描述了许多物理现象，包括光学，力学，等离子体物理学等. KGS方程是薛定谔方程的狭义相对论形式，在等离子体物理学中的作用不容忽视.由于KGS方程并不是完全可积的，因此对其进行数值研究是非常有必要的. 对于非线性薛定谔方程，Debussche等人[2]在数值上模拟了随机非线性薛定谔方程的形态，并设计了自适应算法来提高数值算法的效率以便于准确刻画爆破现象. Feng X等人[3]提出了近似一般非线性薛定谔方程的时间步长格式，并通过数值实验验证了收敛性. 对于KGS方程，已有许多学者研究了其解的性质[4-9]，如：解的存在唯一性、适定性，解的类型(孤立波解、平面波解、周期波解)等. 近年来，张鲁明等人[10-13]对KGS方程构造了差分格式，并做了收敛性分析；石启宏等人[1，14]对有限时刻爆破问题进行了研究.

本文安排如下：第2部分，构造了一种有效的有限差分格式，进行了守恒性分析，为数值求解离散系统设计了不动点迭代算法；第3部分，通过数值算例验证了该格式的收敛性，并观察了爆破现象；最后，进行了总结.

2 差分格式

基于以上符号，给出如下的有限差分格式：

(7)

(8)

(9)

(10)

假设(8)式在n=0时成立，此时(8)式与(9)式联立可得

(11)

2.2 差分格式的守恒性

引理1如果ψ0∈H1，u0∈H1，u1∈L2，那么差分格式(7)-(10)满足下面的守恒性质：

Mn=‖φn‖2=Mn-1=…=M0，

(12)

(13)

‖φn+1‖2-‖φn‖2=0.

(14)

(15)

联立(14)式与(15)式，可得

令

可知，εn=εn-1=…=ε0.

2.3不动点迭代算法为了求解非线性离散系统(7)-(10)，设计如下的不动点迭代算法[15].

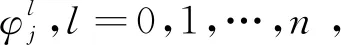
(16)

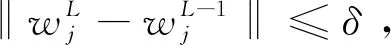
此时，非线性方程转化成一组线性的方程.φ0,U0由(9)-(10)式给出，U1由(11)式计算得到，利用(16)式计算得到φ1，利用(8)式计算得到U2，...,反复迭代可得φn,Un,n=2,3,4,…,N-1，从而可以计算得到φn+1.

3 数值算例

算例1考虑问题(1)-(4)，令λ=0,x0=-10,μ=0.8，耦合KGS方程孤立波解为

其中μ是孤立波的传播速度，x0是初始常数，初始条件如下：

为了验证所给出的差分格式的收敛阶，取x∈[-40,40],T=10，选择空间步长为h=τ.

表1 不同剖分下数值解φn和Un的L误差及相应的收敛阶

表1 不同剖分下数值解φn和Un的L误差及相应的收敛阶

表1显示了λ=0时差分格式的L误差及收敛阶，此时差分格式是2阶收敛的.

算例2考虑问题(1)-(4)，令λ=25，p=5，初始条件如下：

由文献[1]可知，此时方程的解可能会在有限时间内爆破.

图1 ψ和u的数值解(h=0.01,τ=0.01)

图1中(a)和(b)描绘了ψ和u的数值解随时间变化的轨迹，由图1(a)可以清晰地观察到奇点的形成，图1中(c)和(d)描绘了其解L范数的变化. 由于非线性薛定谔方程奇点的形成是要求小尺度的，所以已有的数值结果表明，如果最后|ψ|变为初始条件时给定初值的三倍，就可以认为该解有奇点[3].

4 结 语

本文通过传统的有限差分法对KGS方程进行了研究，对一类非线性KGS方程设计了一种有效的有限差分格式, 证明了在离散意义下差分格式满足质量和能量守恒. 通过数值实验，验证了该差分格式的二阶收敛性，并模拟了在某些初始条件下KGS方程可能会发生爆破. 近年来，基于IEQ数值方法的研究越来越广泛，但对于高维KGS方程数值方法的研究还比较少，以后将对高维KGS方程的数值模拟做更深入更广泛的研究.