基于BP神经网络的300 MW循环流化床机组出力预测

韩义，张奇月，王研凯，于英利，付旭晨，荣俊，段伦博*

（1.内蒙古电力（集团）有限责任公司内蒙古电力科学研究院分公司，呼和浩特010020；2.东南大学能源热转换及其过程测控教育部重点实验室，南京210096）

0 引言

蒙西电网［1］网架结构复杂、驾驭难度大，电网统调装机6.599 GW，500 kV 变电站26 座，220 kV 变电站146 座，110 kV 及以下变电站932 座，系统较复杂；承担大量的西电东送、蒙电外送任务，若大量负荷不就近消纳，将对关键线路造成巨大压力。因此，为了便于电网做出更好的调度安排，保证电网稳定运行，进行出力预测变得尤为重要。

随着机器学习技术的不断进步，各种行业均开始应用机器学习来解决实际问题，通过大数据技术解决传统数据解决不了的问题。与传统数据相比，大数据在数量、多样化、价值以及更新速度上具有明显的优势［2］。随着分散控制系统（DCS）、厂级实时监控信息系统（SIS）、管理信息系统（MIS）以及其他辅助控制系统［3］的广泛应用及不断改进，各电厂及电力集团公司存储了大量的运行数据及化验数据，形成了覆盖电站机组生产全过程的数据库，这些数据包含大量的隐含信息，以数据为中心的信息化理念将极大地变革电力信息化方式［4-8］。

煤质变化等原因造成机的组出力不稳定不利于电网调度。因此，提供合适的出力预测方案可以方便电网做出合适的调度安排，避免不必要的风险。基于从头计算的机组负荷预测自然可以有较高的准确性，但其需要输入的参数太多，且大多不能在线测量。以本文研究的循环流化床机组为例，如果通过在线测量煤质、飞灰含碳量等参数来准确计算锅炉热效率，自然可以实现负荷的预测，但是技术难度大且计算量可观，难以实现实时应用。如果采用大数据理论，则可以避免直接测量这些数据，直接寻找关键参数和机组出力的关系。同时，通过这一关系，也能反馈机组出力对关键参数的范围要求，从而界定机组的边界出力。

徐游波［9］提出汽轮机的运行状态随着蒸汽流量、温度及压力等因素的变化而变化，通过对历史运行数据的分析，得出机组出力与主蒸汽流量大致成正比例变化趋势的结论。通过拟合机组出力与主汽流量的关系计算出力，实现汽轮机侧基于历史运行数据的机组负荷预测。该研究虽然可以解决出力预测问题，但随着时间的推移，拟合函数的计算精确度会不断降低。

本文提出通过搭建BP 神经网络模型并利用大数据来进行出力预测。利用滑动窗口法，当有新的数据样本进入模型时，直接剔除最旧样本，更新模型参数，解决了随着机组的状态改变，原有模型的准确性和精度降低、泛化性能下降的缺点［10-12］。相比于模型重构，大大减少了计算量及模型更新所用时间。本文以相关参数数据为网络的输入层，以机组出力为输出层，训练网络模型，通过调节相关参数值进行仿真试验，最后得到最优网络模型。

1 研究方法

1.1 研究对象

本文针对某300 MW 循环流化床机组，该机组锅炉为单汽包、自然循环、循环流化床燃烧方式，由1个膜式水冷壁炉膛，3台汽冷式旋风分离器和汽冷包墙包覆的尾部竖井组成。汽轮机为亚临界、高中压合缸、一次中间再热、单轴、双缸双排汽、直接空冷凝汽式，配有2个主蒸汽阀门、6个高压调节阀门、2个中压主蒸汽阀门、2个中压调节阀门。锅炉设计汽水参数及汽轮机设计参数见表1—2。

选用来自此电站系统中存放的海量历史数据，主要包括发电机有功功率、主蒸汽流量和其他管道测点共计48 个不同参数的信息。选取了其中一段时间，每分钟一个参数取一个数据，即便只有5 d 时间，总数据量仍然十分巨大。如果要靠传统的人为分析，困难系数是相当大的。以主蒸汽流量及其他相关参数为输入，发电机有功功率为输出，建立基于BP神经网络的机组出力预测模型，从而对机组出力进行预测。

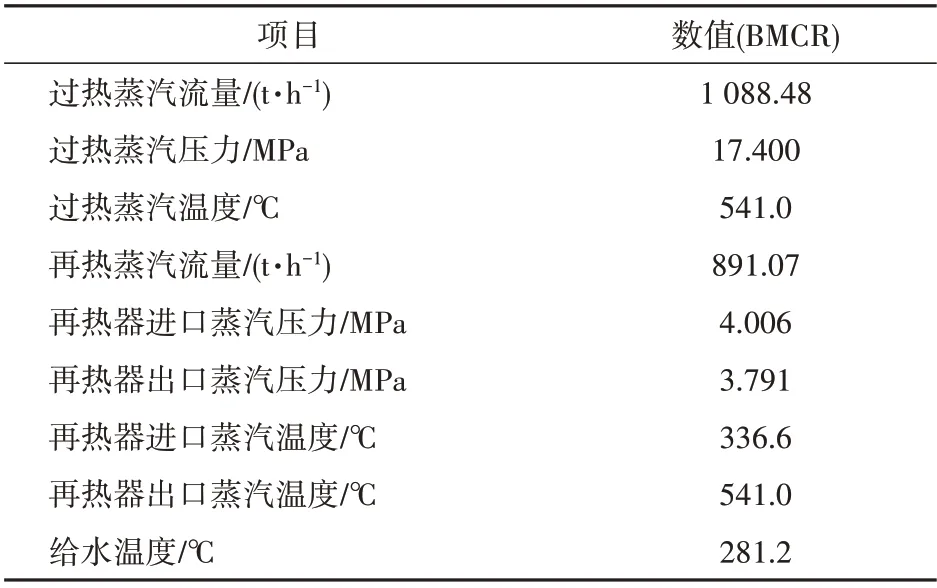
表1 锅炉设计汽水参数Tab.1 Design steam-water parameters of the boiler

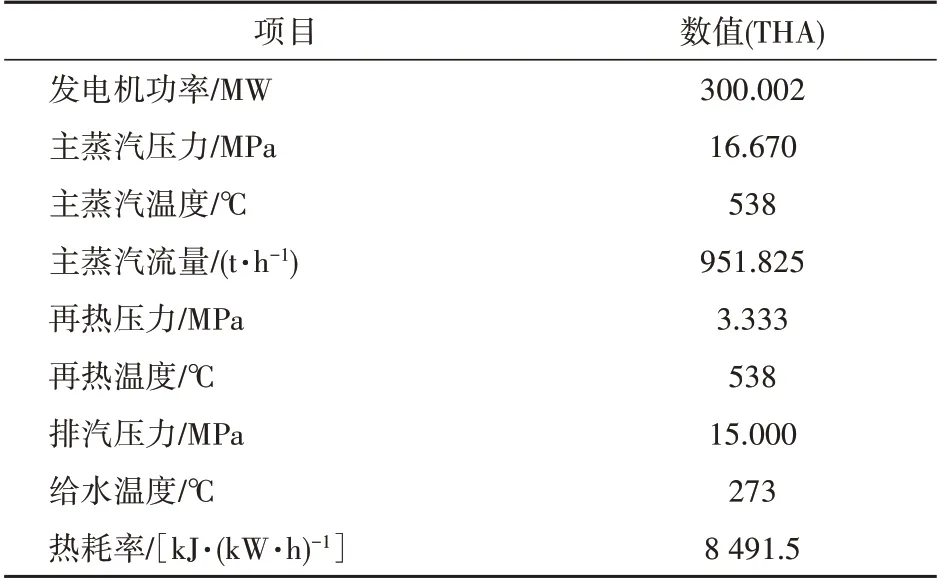
表2 汽轮机设计参数Tab.2 Design parameters of the steam turbine

1.2 BP神经网络

BP神经网络是一种多层前馈型神经网络，可以实现从输入到输出的任意非线性映射［13］。典型的BP网络结构如图1所示：输入层具有R个输入；隐层具有S个神经元，采用S型传递函数。

隐层的非线性传递函数神经元的作用为学习输入与输出的线性及非线性关系，由于在进行训练之前一般都会进行数据的归一化处理，所以一般会通过线性输出层拓宽网络输出。BP 神经网络具有很强的非线性映射能力、高度的自学习和自适应能力、一定的容错能力，在局部神经元受到破坏后，对全局的训练结果不会造成大的影响。

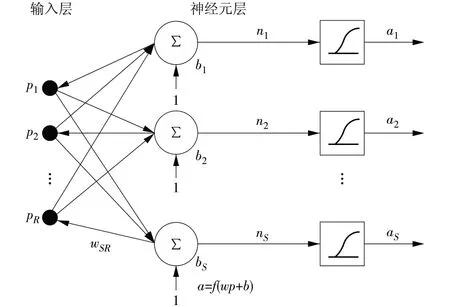
图1 BP网络结构Fig.1 BP network structure

BP神经网络在应用方面主要用于函数逼近、模式识别、分类、数据压缩4方面。本文主要通过相应的输入与输出来训练一个网络以逼近一个函数，达到预测出力的目的。

1.3 数据预处理方法

大型燃煤发电机组所包含的系统众多，数据复杂，且大量的数据中必然存在错误数据。为了提高模型的精确度，对数据进行预处理是十分必要的。

1.3.1 异常数据的剔除

对于大数据建模而言，需要的数据量很大。但是，在实际的测量过程中，仪表的精确性、外界的干扰、测点的选择、传感器的故障等均会导致其中部分数据受到污染。如果在建模之前不对这些污染数据进行剔除，模型的精确性就会受到影响。谭浩艺［14］等人曾经通过拉依达准则（即3σ 准则）对数据进行预处理，将明显误差较大的数据剔除。拉依达准则是指先假设一组检测数据只含有随机误差，对其进行计算处理得到标准偏差，按一定概率确定一个区间，认为凡超过这个区间的误差，就不属于随机误差而是粗大误差，含有该误差的数据应予以剔除。在测量次数充分多的情况下，数据的误差必然趋于正态分布，因此，电厂大数据刚好适合用来剔除异常数据。

1.3.2 数据的归一化处理

该模型涉及的参数很多，不同参数之间、同参数之间的样本数据也可能存在较大差距。例如，主蒸汽流量数值最高达到1 000 t∕h 以上，而各类换热器进出口的蒸汽压力数值却只有10 MPa 左右。如果样本数据之间的数值差距过大，神经网络模型的训练时间会变长，训练后的模型精准度也不够。因此，在确定了各个参数之后，在输入数据之前，最好对数据进行归一化处理［15］。假设参数原值为a，归一化处理后的值为b，同类型参数最大值为amax、最小值为amin，则两者之间的关系用公式表示为

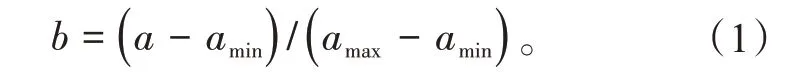
1.3.2 PCA降维

选择合理的模型变量对于建模来说十分重要。燃煤发电机组包含众多的子系统，如给煤系统、燃烧系统、给水系统、送风系统等，每个子系统都与众多的参数相关联。从所有可能对机组出力有影响的参数中选出关系较为密切的特征参数作为模型的输入量，可以获得近似或是更好的模型性能。通常研究人员选择模型变量都是依据长期的经验。然而有时候并没有完备的理论依据，如果选择了一些不重要的自变量，模型的精度会降低。本文选用Matlab软件中自带的PCA降维函数对大数据进行主成分分析［16-17］，在新的参数坐标下获取每个主成分所占的影响值，直观地选择所需要降的维数。

2 基于BP神经网络的出力预测模型建立

2.1 BP神经网络模型建立

本研究选取了连续960 个时间点的样本数据，训练时选取所有时间点的数据，测试验证选用后460 个时间点的数据。基于BP 神经网络的机组出力预测流程如图2所示。

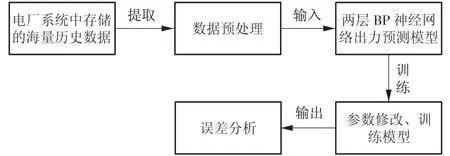
图2 机组出力预测流程Fig.2 Flow of power unit output prediction

首先对主蒸汽流量及其他相关特征参数进行异常数据剔除、归一化，以及降维预处理。利用PCA 函数对所有相关参数进行处理之后，可以得到输出影响值，即每一个主成分所贡献的比例，可以更直观地选择所需要降维的组数。经过数据处理发现仅主汽流量所占的比例就达到了96.33%，其次依次是高温过热器出口蒸汽压力、高温过热器出口蒸汽温度、屏式再热器出口蒸汽压力、屏式再热器出口蒸汽温度、锅炉给水温度、有效床温，分别占比1.78%，0.80%，0.37%，0.20%，0.11%，0.08%。这与徐游波［9］结论相接近。因此，综合考虑将输入层数据维数降到7，这样整个影响比例之和便超过99.90%，其他因素可以忽略不计。

BP 神经网络通过误差信号不断反向传播来减小输出值与期望值的误差，达到训练网络的目的。在该过程中，隐层神经元数量会影响误差大小。因此，确定BP神经网络的隐层神经元数量很重要。神经网络预测模型一般选用均方根误差［18-19］和相对误差［20］作为评价指标。均方根误差和相对误差的计算公式如下所示

式中：RMSE 为均方根误差，MW；ypredict为预测值，MW；yreal为期望值，MW；n为总预测时间点数。

通过统计各神经元数量下BP 神经网络模型输出值与期望输出值的相对误差Error 及均方根误差RMSE，选取最合适的神经元数量。隐层神经元数量从1 到9 进行试验后，输出值与期望输出值的平均相对误差以及均方根误差如图3所示。

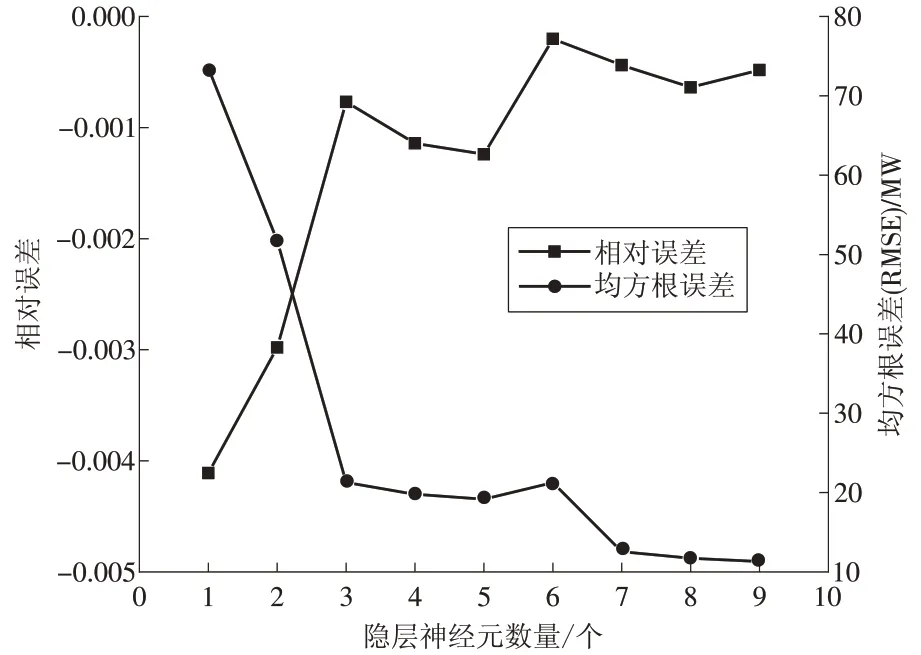
图3 输出值与期望值的相对误差Fig.3 Relative error between the output value and its expected value

由图3 中可以看出，当隐层神经元的数量增加到7 的时候，BP 神经网络模型的输出值与期望值的平均相对误差低于1%，此时的均方根误差约为13.4 MW，再增加神经元数量模型的精确度也不会得到大的改善。因此，隐层神经元的数量选择为7。

2.2 BP神经网络的训练结果分析

当隐层神经元数量为7 时，机组出力的预测值与实际的期望值的曲线如图4 所示，预测值与期望值的相对误差如图5所示。

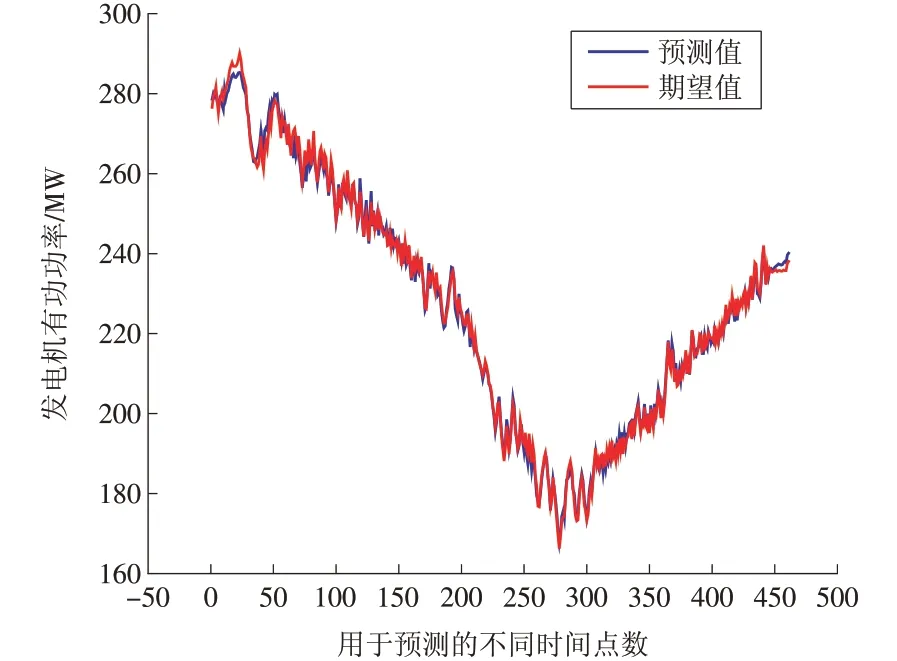
图4 BP神经网络预测值与期望值的对比Fig.4 Comparison of the predicted value and the expected value made by BP neural network

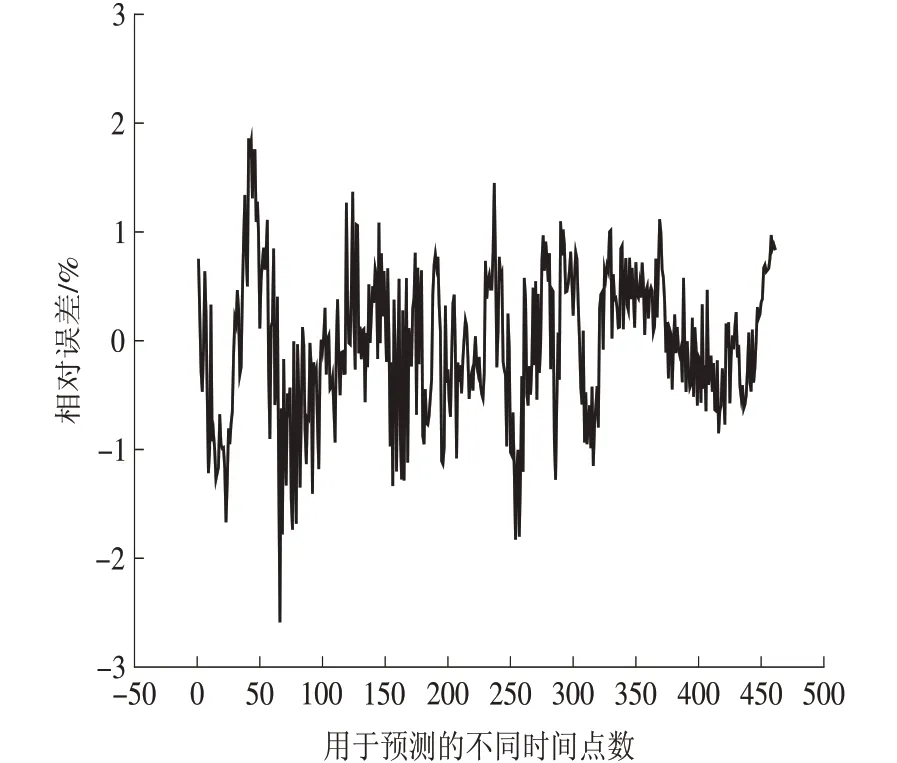
图5 BP神经网络预测值与期望值的相对误差Fig.5 Relative error between the predicted value and the expected value made by BP neural network

应用BP 神经网络预测模型预测得到的预测值曲线与实际的期望值曲线接近重合，验证BP神经网络模型有良好的预测精确度。预测值与期望值的相对误差除了极个别点以外，都在±2%的范围内。因此，模型的预测稳定性也较高，可以满足需求。

2.3 基于BP神经网络的出力预测

选用训练数据外别的时间点的样本数据来检验模型的精度，为了保证模型精度的覆盖范围，选用6个不同范围的数据，原始数据见表3。

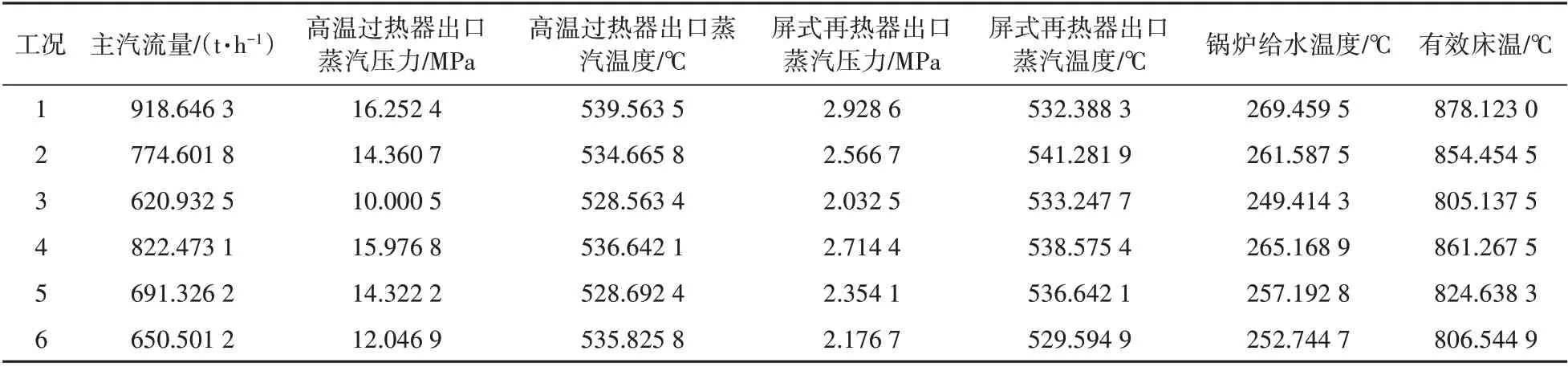
表3 BP神经网络的各项输入值Tab.3 Inputs of the BP neural network

将下列变量作为输入量，经过模型预测获得的预测值与期望值的对比见表4。经过预测，可以发现误差基本都在1%以内，模型的精度较高，值得信赖。

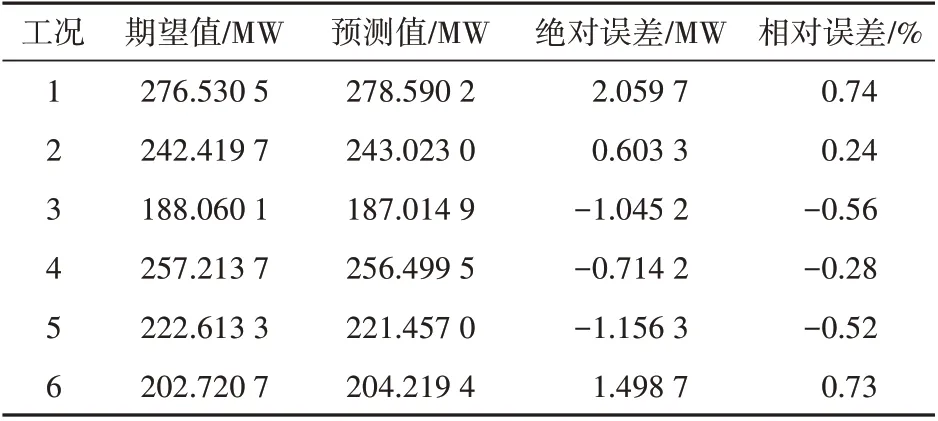
表4 预测值与期望值的对比Tab.4 Comparison of predicted and expected values

3 结论

采用BP 神经网络结合数据预处理和PCA 降维，以某300 MW 循环流化床机组为对象建立机组出力预测模型。经过主成分分析发现，主蒸汽流量是影响机组出力的最主要因素，其影响程度达到了96.33%。

高温过热器出口蒸汽压力、高温过热器出口蒸汽温度、屏式再热器出口蒸汽压力、屏式再热器出口蒸汽温度、锅炉给水温度、有效床温也有一定影响，分 别 占 比1.78%，0.80%，0.37%，0.20%，0.11%，0.08%。误差分析表明，隐层含有7 个神经元即可达到较高的模拟精度。

利用BP 神经网络机组出力预测模型对460 个时间点的数据进行验证试验，结果表明，该模型与实际运行数据吻合良好，相对误差在±2%以内，使用训练样本外时间点的数据进行预测，相对误差也在±1%以内，精度较高。

该研究为循环流化床机组出力预测提供了方法。在电网面对电力调度问题时，通过该出力方法可以有效预测各个火电机组的出力，从而对调度提供有力指导。