基于EMD分离水压分量的重力坝变形参数反演分析

张丽，田紫圆

（1.华电金藏物资成都有限公司，成都610041；2.四川大学水利水电学院，成都610065）

0 引言

随着经济的发展和社会的进步，人们对大坝安全监测重要性的认识不断提高［1］。对大坝安全监测资料进行分析，建立监控模型和相应的安全评价指标是保障大坝安全运行的重要手段［2］。在混凝土坝的安全监控中，常采用数值模拟方法评价大坝的强度和稳定性，而坝体和基岩力学参数是影响数值模拟准确性的关键因素［3-5］。

近年来，结合大坝原型观测资料反演坝体和坝基材料参数越来越受到重视［2］，张梦溪［6］在构建变形混合模型时，采用混凝土重力坝等几何离散仿真模型，反演分析得到坝体混凝土材料参数，进而通过改变上游水位高度，求出混合模型中的水压分量；王建等［7］利用重力坝水平位移监测资料，采用TOLMIN 容错算法进行大坝弹性模量反演，建立了多测点混合模型，其结果显示，相比单测点混合模型，2 个测点的多测点混合模型反演和拟合精度更高；彭圣军等［8］利用统计模型分离出不同水位工况下的水压分量相对值，采用最小二乘支持向量机进行大坝弹性模量的反演，构建变形监测混合模型。随着智能优化算法的不断改进，神经网络法、粒子群法、麦夸特法、遗传算法、通用全局优化算法等最优参数求解方法被不断应用于反分析过程中。王刚等［9］以大坝和基岩的弹性模量作为反分析参数，利用改进的遗传算法进行了有限元反演分析。田泽润等［10］基于有限元计算得到的响应面函数，采用遗传算法求解参数反分析的目标函数，得到效果良好的反演参数。

采用统计模型［11］分离大坝位移等监测数据的水压分量，再根据水压分量进行大坝参数反演分析是目前常用的方法。由于统计模型中时效因子的函数形式是人为事先设定的，可能无法准确模拟监测数据实际的时效分量，从而影响水压分量的准确分离，因此，本文采用经验模态分解（EMD）技术［12］剔除重力坝位移、应变监测数据中的时效分量后，再分离水压分量，可以有效提高水压分量分离的准确性。为提高参数反演分析的效率，本文采用响应面代理模型替代耗时的有限元计算构建参数反演的目标函数，再利用遗传算法对重力坝坝体和坝基的材料参数进行反演分析。

1 基于EMD分离水压分量的参数反分析方法

1.1 EMD基本原理

EMD 算法假设任何复杂的时间序列都由一些相互不同的固有模态函数（IMF）分量组成，每个IMF 可以是线性或非线性的，其本质是通过设定的算法将信号逐级分解，生成一系列不同特征尺度和频率的IMF。在分解出不同频率的IMF 之后，剩余的残余信号即为信号中频率最低的成分，为信号数据序列中的时效趋势分量，即

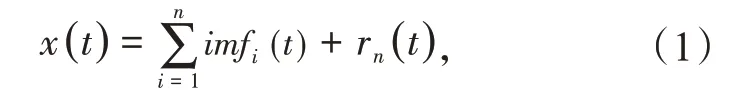
式中：x(t)为原始信号；imfi(t)(i = 1，2，…，n)为x(t)通过EMD 分解得到的n 个固有模态函数；rn(t)为剩余的残余信号或常量。

对信号进行EMD 分解，每个固有模态imfi(t)(i = 1，2，…，n)相互独立。固有模态2个零点之间的每个波动周期中不存在多重极值点，是EMD中分解数据序列的基本单元。其中，每个IMF 必须满足2个条件：（1）极值点与零点的数量之差不大于1；（2）局部极大、极小值点确定的上、下包络线的均值为零，即上、下包络线关于时间轴对称。

1.2 响应面代理模型

响应面代理模型［13］是根据结构性能响应数值试验结果得到的高维超曲面，是替代相对耗时的有限元计算的一种近似模拟方法。根据不同参数组合的有限元数值模拟结果，本文使用正交设计［14］和非线性回归分析，构造不含交叉项的三次多项式响应面代理模型，见式（1）。代入材料参数（如弹性模量）和库水位后，即可快速计算重力坝的位移和应变。

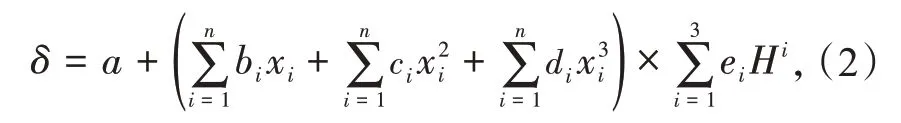
式中：a，bi，ci，di，ei为响应面模型系数，可以采用差分进化算法求得；n 为待反演的重力坝材料参数个数；xi(i = 1，2，…，n)为第i 个待反演的重力坝材料参数；H，δ 分别为正交试验样本对应的上游水深和有限元模拟值。

1.3 参数反演的目标函数

本文在重力坝材料参数反演分析中，根据增量反演原理，通过不同库水位变幅对应的实测位移、应变增量和响应面模型计算的位移、应变增量的相对误差平方和构建目标函数。参数反分析的目标函数为

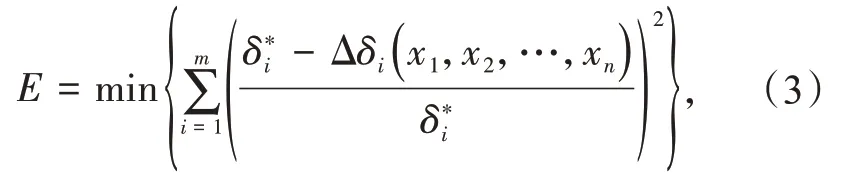
1.4 遗传算法

遗传算法（GA）［15］是参数反分析中应用最广泛的优化算法之一，其算法本质是通过遗传算法的复制、交叉和变异不断推动整个种群进化［16］。

在本文重力坝材料参数反分析中，结合响应面模型和基于EMD 分离的水压分量构建目标函数后，就可以利用遗传算法得到材料参数的最优组合。

本文遗传算法采用实数编码的形式，交叉方法采用均匀交叉法，主要步骤如下。

（1）进行实数编码。

（2）设定种群规模G（即种群中所含个体数量）、染色体选择的交叉概率Pc、交叉方法、变异概率Pm以及变异方法等。

（3）生成初始种群。根据参数的取值范围[xmin，xmax]，将生成的均匀分布随机数赋值给基因值。

（4）种群中个体适应度评价。本文设定个体适应度F(X)为相应目标函数值f(x)的负值，即

（5）选择操作。采用轮盘赌选择法，个体Xi被选中遗传至下一代的概率为

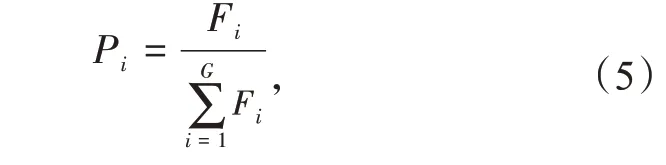
式中：G为种群规模；Fi为个体Xi的适应度。

（6）交叉操作。采用均匀交叉方法，以交叉概率Pc对父代个体X1和X2进行交叉操作，产生的子代个体X'1，X'2为

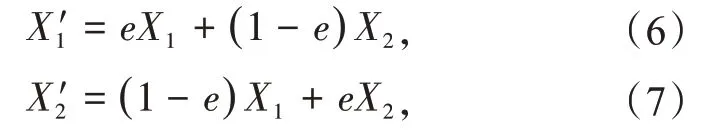
式中：e 为比例因子，是(0，1)范围内均匀产生的一个随机数。

（7）变异操作。个体Xi中的基因位以概率Pm发生变异，即以Pm的几率在参数区间[xmin，xmax]中均匀抽取随机数代替原有基因位。

（8）设置目标函数收敛准则或最大迭代次数，当目标函数之差小于一定值或达到最大迭代次数时算法结束。此时，种群中最优个体代表的材料参数值即为遗传算法优化得到的最佳参数组合。若不满足终止条件，则转向步骤（4）。

2 工程应用

2.1 工程概况

YL水电站枢纽主要由拦河碾压混凝土重力坝、泄洪消能建筑物、引水发电建筑物等组成，属日调节水库。YL 碾压混凝土重力坝自左至右依次布置左岸挡水坝段、河床溢流坝段（左、右侧溢流坝段内设2 个中孔）、右岸挡水坝段。YL 重力坝的最大坝高为138 m。

2.2 有限元模型及材料参数

本文采用YL 重力坝#13 坝段坝顶TP9 测点的顺河向位移和坝体应变计S3-1 测点的应变进行坝体和地基弹性模量反分析。采用ANSYS 软件建立YL重力坝#13坝段三维有限元模型，有限元模型的模拟范围为：上、下游方向和自建基面向下均延伸2.5倍坝高（约370 m）。模型X 轴以上游指向下游为正，Y轴以竖直向上为正，Z 轴以左岸指向右岸为正。有限元模型采用8 节点六面体SOLID45 单元进行剖分，整个模型共划分为58 452 个单元和65 931 个结点。为方便有限元计算值与实测值的对比，根据TP9 和S3-1 测点的布设位置在有限元模型中的相应位置布置特征点，用于提取计算结果。

YL 重力坝#13 坝段有限元模型及坝体、地基材料分区如图1所示，设计采用的材料参数见表1。

2.3 参数正交设计与响应面模型构建

由于泊松比对重力坝应力变形的影响较小［17］，因此，本文主要对坝体混凝土R1，R2，R3，R4，R5，C2 和基岩2，3（1），3（2）类的弹性模量进行反分析，共计9个材料参数。根据各材料弹性模量的设计值确定其合理变化范围，在正交设计时，弹性模量根据其变化范围按7个水平取值。选择上游库水位时应包含最低、最高库水位，因此，分别选择129.33，132.00，134.67，136.00，138.67，141.00，144.00 m共7 组水位进行有限元计算。由于下游水深较小，故在计算中未考虑。

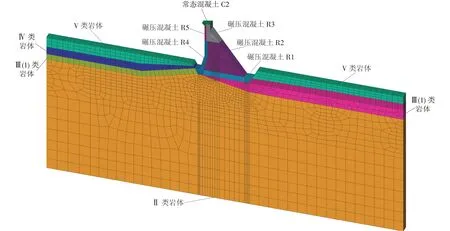
图1 YL重力坝#13坝段有限元模型及坝体、坝基材料分区Fig.1 Finite element model of YL Gravity Dam #13 dam section and material division for the dam body and dam foundation

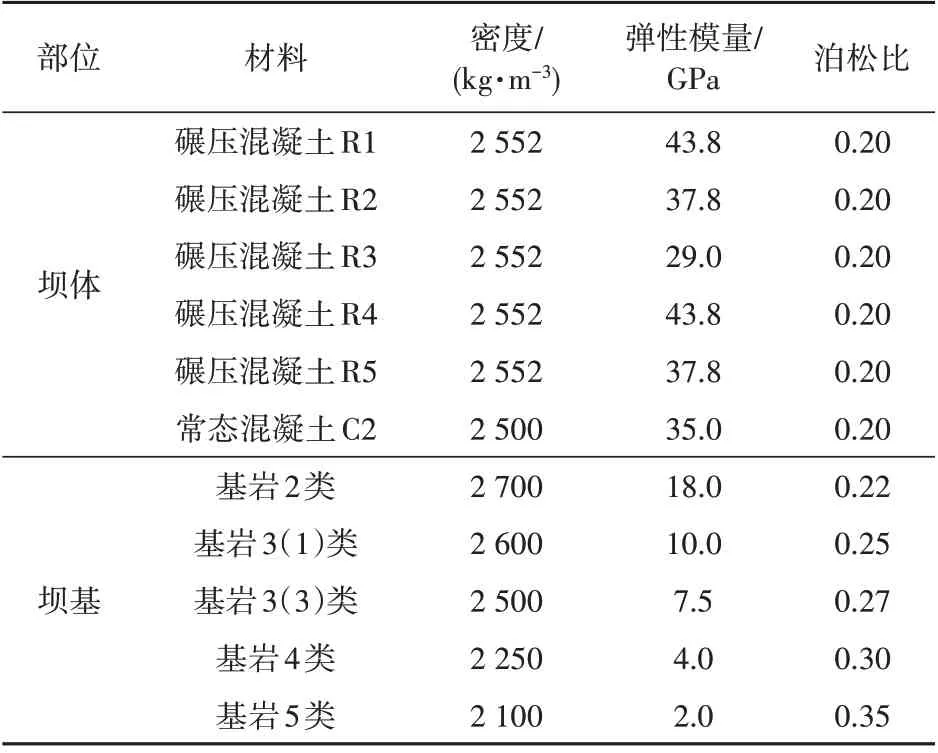
表1 坝体及坝基材料的设计参数Tab.1 Design parameters of materials for the dam body and dam foundation

通过10参数7水平正交设计，共获得81组参数样本。根据7 组库水位，利用建立的有限元模型计算81组参数样本对应的坝顶位移和坝体应变，再采用不含交叉项的三次多项式构建响应面代理模型。检验表明，坝顶位移（TP9测点处）和坝体应变（S3-1测点处）响应面代理模型的复相关系数分别为0.97，0.99，均大于0.95，说明本文构建的响应面代理模型对于YL重力坝#13坝段位移和应变的拟合效果良好，可用于后续的参数反分析。

2.4 坝体与坝基弹性模量反演结果

采用EMD 剔除TP9 测点顺河位移和S3-1 测点应变监测数据序列的时效分量，再通过统计回归方法［4］分离出各监测数据序列的水压分量。根据增量反演原理，通过不同库水位变幅对应的实测位移、应变增量和响应面模型计算的相应增量的相对误差平方和来构建目标函数。

本 文 选 取2015 年5 月1 日 和2015 年8 月20 日作为计算TP9 测点顺河向位移和S3-1 测点应变增量的初始时刻，利用2015年5月2日至2017年5月1日期间的位移监测数据（共659 个数据）、2015 年8月21 日至2017 年5 月1 日期间的应变监测数据（共531 个数据）的水压分量构建目标函数，最后采用遗传算法，按目标函数值最小的原则进行参数寻优。遗传算法采用实数编码模式，种群数设置为20，交叉方法选择为均匀交叉，交叉概率为0.85，变异概率为0.01。坝与地基弹性模量的约束区间和反分析结果见表2。

表3为采用设计参数与反演参数模拟的水压分量与实测水压分量的误差。由表3 可见：对于TP9测点的顺河向位移，与实测水压分量相比，采用反演参数模拟的水压分量的误差远小于采用设计参数模拟的水压分量误差；对于S3-1 测点的应变，采用设计参数与反演参数模拟的水压分量的误差大致接近。总体而言，采用反演参数能准确地模拟各测点监测数据的水压分量，表明重力坝坝体与坝基弹性模量参数反分析效果良好，有限元模型的水压分量模拟值与实测值吻合较好，可以反映实际情况下测点位移与应变的水压分量。

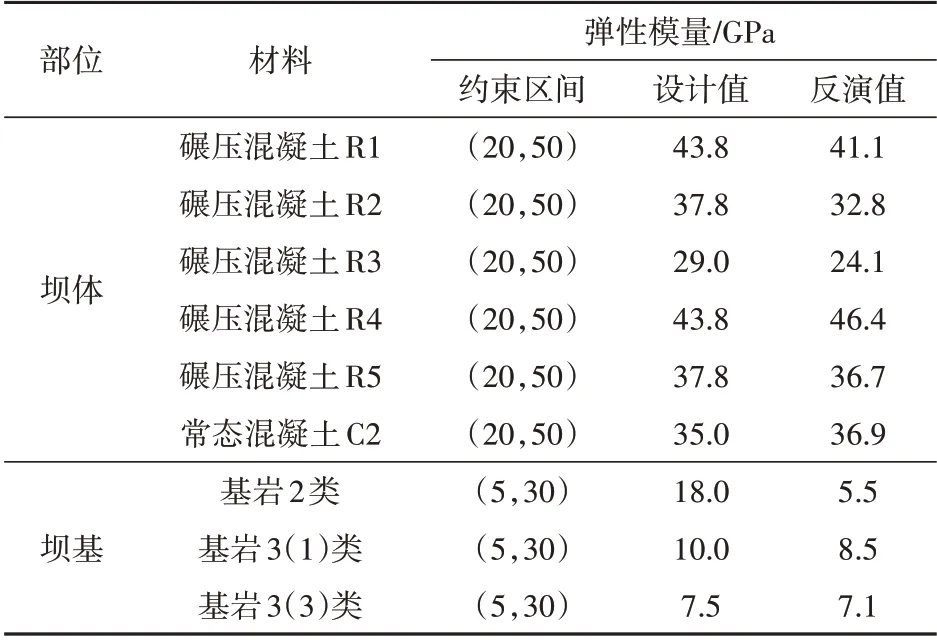
表2 YL重力坝#13坝段坝体、坝基弹性模量反分析结果Tab.2 Back analysis results of dam body and dam foundation's elastic modulus for YL Gravity Dam #13 dam section

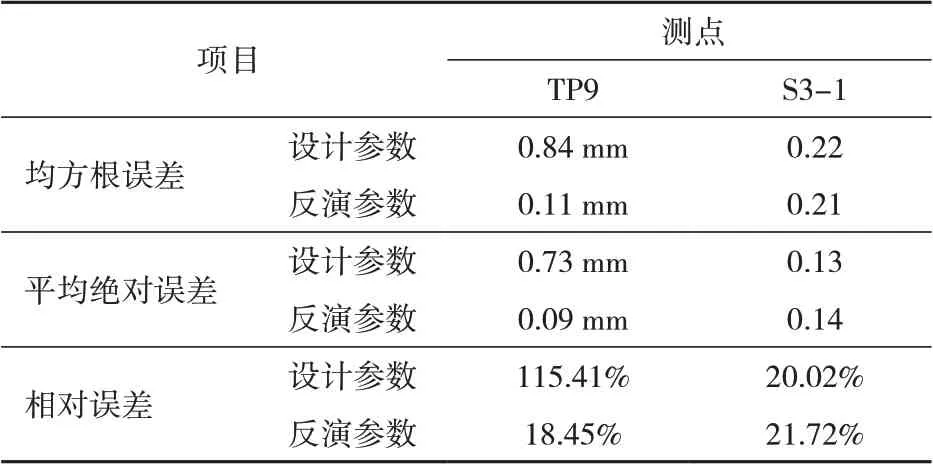
表3 采用设计参数与反演参数模拟的水压分量误差Tab.3 Error of water pressure components simulated based on design parameters and inversion parameters

图2 和图3 为采用反演参数计算的TP9 顺河向位移、S3-1 应变的水压分量和实测值的对比。由图2和图3可知，基于反演参数模拟的水压分量与实测值吻合较好，可以比较准确地反映各测点位移与应变的变化规律。

图4 为采用设计参数与反演参数计算的YL 重力坝应力分布图。由图4 可以看出：按设计参数与反演参数计算的应力分布有较大差别；按反演参数计算的应力总体大于按设计参数计算的应力，考虑应力集中现象，坝体最大应力均出现在坝踵处，采用设计参数和反演参数计算的坝体最大压应力分别为3.6 MPa和4.7 MPa。

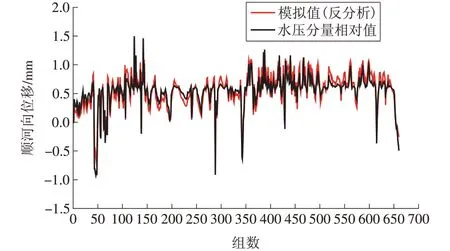
图2 TP9顺河向位移水压分量反分析结果与实测值对比Fig.2 Water pressure component of the displacement at TP9 along river made by back analysis and measurement

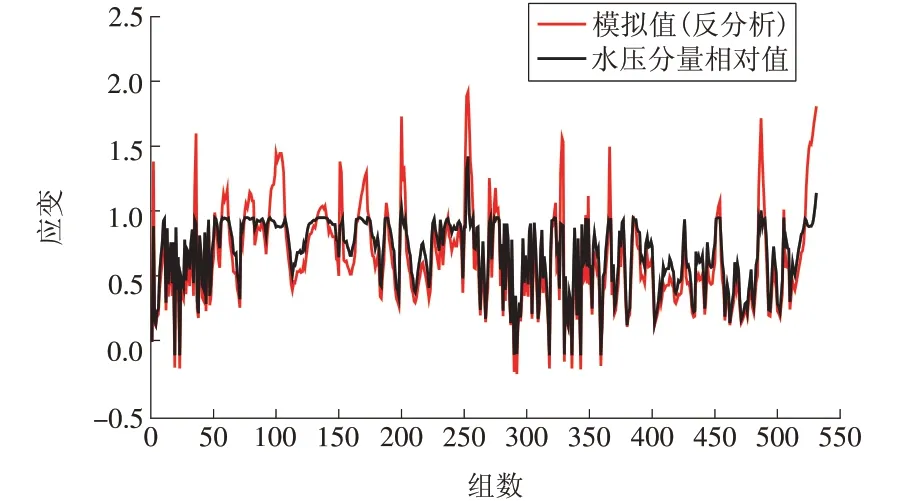
图3 S3-1应变水压分量反分析结果与实测值对比Fig.3 S3-1 strain water pressure component made by back analysis and measurement

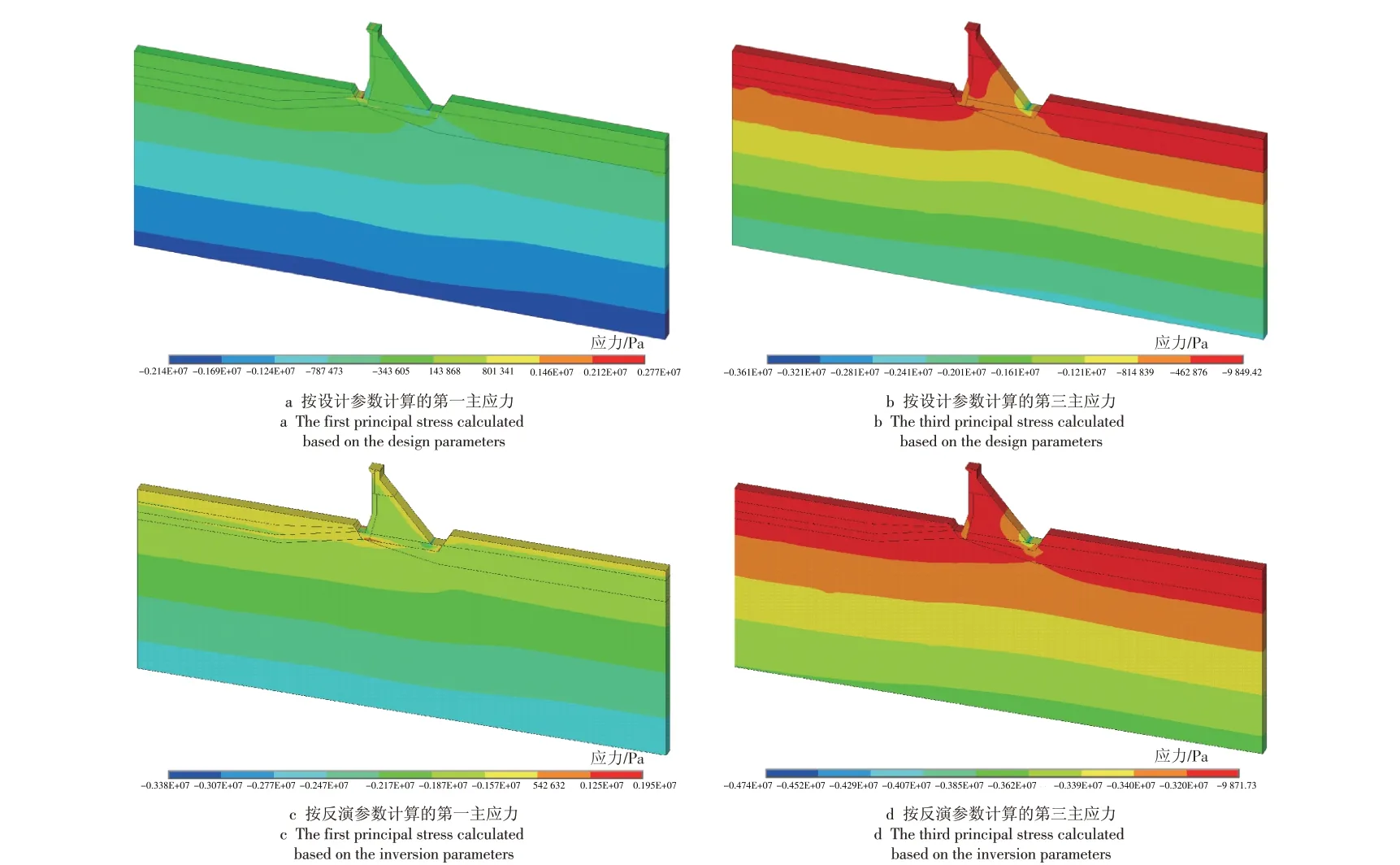
图4 YL重力坝#13坝段应力分布云图Fig.4 Stress distribution contours of YL Gravity Dam #13 dam section

3 结束语

本文提出了一种利用EMD 技术剔除重力坝监测数据的时效分量再分离水压分量的方法，有助于提高水压分量分离的准确性；同时，结合响应面代理模型和遗传算法，提高了重力坝参数反分析的效率。

以YL 重力坝#13 坝段为例，根据其坝顶顺河向位移测点TP9、坝体S3-1 应变计测点的实测数据，采用本文提出的方法对该坝段坝体和坝基的弹性模量进行了反演，参数反演结果在合理范围内。反演结果表明，与设计参数相比，采用反演参数模拟的坝体位移水压分量与实测值更为吻合，可以反映实际情况下测点位移与应变的变化规律，能够更加准确地对该重力坝的工作性态进行分析和解释。