对称美在中职数学教学中的巧用
2021-01-08黄振贵
黄振贵

[摘 要] 中等职业学校的学生在初中阶段由于多种原因导致理论基础知识相当薄弱,甚至不少学生出现知识断层,一些重要的数学定义、公式、定理都遗忘得差不多了。在一线中职数学教学多年,听到学生说过最多的一句话是:“如果数学能学得好的话早就选择读高中了,不至于选择读中职了。”印象深刻的是曾经有一个学生在他的数学书本封面上写着这么一句话:“忘记一个人怎么那么难,而忘记数学却那么容易啊!”这也道出了无数中职学生的困境和无奈,由于他们没有扎实的知识基础,要学习新一级的理论知识难免会遇到各种困难,特别是数学这种需要基础理论做衔接的学科,没有基础知识做铺垫的话要学习起来难上加难。这也给中等职业学校的一线教师具体教学上带来很大困惑,针对此困惑,提出对称美在中职数学教学中的巧用,为了尽量避开数学的学习或解题需要强大的理论支撑才能完成。数学对称美的思想理念和思维可以化抽象为形象,能快而准地解决实际的数学问题。由于数学对称美的直观性可以让更多不同基础层次的学生,甚至零基础的学生参与到具体的教学中,引导利用对称思维帮助他们独立观察、发现、分析、解决问题。通过对称美在代数式求最值、解不等式、利用几何对称求最值、函数奇偶性的判断、数列运算等问题的解析,并通过教材中对称美的案例来验证在数学教学及解题中的巧用。
[关 键 词] 数学对称美;中职数学;构造对称;数学解题
[中图分类号] G712 [文献标志码] A [文章编号] 2096-0603(2021)51-0149-03
一、对称美的背景及意义
2015年9月15日,国务院办公厅印发《关于全面加强和改进学校美育工作的意见》中要求:“加强美育的渗透与德育、智育、体育相融合,与各学科教学和社会实践活动相结合。挖掘不同数学、物理等自然学科中的美育价值。”
笔者觉得中等职业学校的数学教学,如果还是停留在传统的课堂理论教学是完全不能激发学生的学习兴趣,因为普遍中職学生早已厌倦学习数学,不爱主动去独立思考那些理论数学知识,平时很多作业或课后习题都是应付了事的。但是在中职新课标改革和学业水平测试的驱动下,数学是必考科目之一,因此,要让学生从思想上改变对数学的看法,认识学习数学的重要性和必要性,同时老师也在教学中探索新的教学方法,让多数中职学生能不再谈“数”色变。笔者觉得将数学对称美运用到具体的教学中,可以激起更多中职学生学习数学的兴趣,常规的解题需要掌握定义、定理、公式的理论基础做支撑才能解答的,数学对称美能改变此传统解题思维,化抽象为具体,同时也能让所有中职学生把数学对称美这一思想理念带入课堂中,提高教学效率。作为一线中职数学老师,有必要也有责任思考数学对称美给数学学习提供的帮助,同时也能让他们感受数学不一样的美感,不再惧怕无聊的数学理论学习。本文主要从平时教学中的案例来分析,提高学生观察、发现、分析、创新能力,最终培养出社会所需求的各种人才。
二、数学对称美的表现形式
(一)图形的对称美
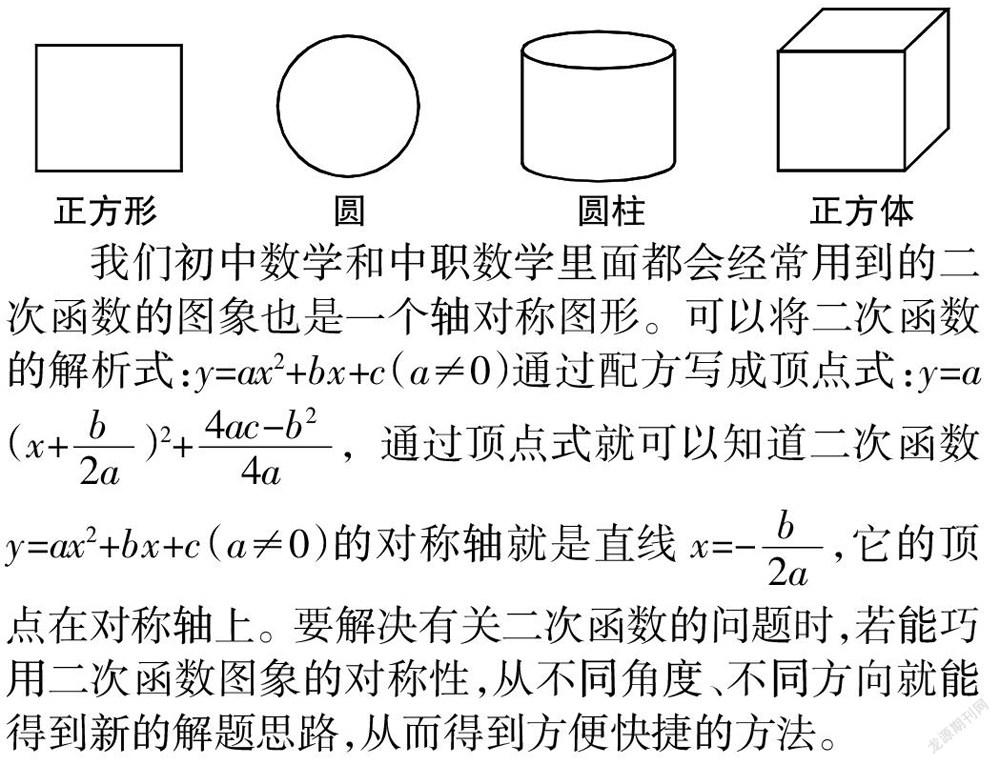
图形的对称是最直观、最形象的,也会让人有不一样的感受,学生接受起来也是最容易。数学的几何图形的对称性就是最直接的视觉表现,具体表现有平面几何或空间几何图形的轴对称和中心对称。比如:正方形是中心对称图形,同时也是轴对称图形;圆也是中心对称图形,所有过圆心的直线都是它的对称轴;圆柱、正方体等图形也可以给人以很多完美的对称性。
(二)代数式的对称美
数学的对称美不只是停留在几何图形上面,代数式的对称美在日常的数学教学中也是无处不在,要通过利用对称美细心的观察和领悟,从中体验数学美的真谛,从而激发中职学生学习数学的兴趣和积极性,改正他们不爱独立思考的学习态度和惧怕数学的心理。正如德国教育家第斯多惠所说:“教学的艺术不在于传授本领,而在于激励、唤醒、鼓舞。”比如,12=1,112=121,1112=12321,11112=1234321,111112=123454321,
1111112=12345654321,11111112=1234567654321……二项式的展开式:(a+b)n=C0nan+C1nan-1b1+C2nan-2b2+……+Cn-1na1bn-1+Cnnbn(n∈Z+),其中C0n与Cnn,C1n与Cn-1n,C2n与Cn-2n……中都展示出了对称美。其中a,b的位置也可以互相对换,对换之后的结果依然成立,这样同样形成一种美丽的对称。南宋时期的数学家杨辉所写的《九章算术》中杨辉三角刚好可以解释了二项式展开式的系数的规律,即二项式定理。同时二项式定理和杨辉三角的数形结合走进了数学,可以从中发现和挖掘更多的奥秘,多角度运用到实际的数学解题中。数学对称美,也需要我们去挖掘、去观察、去探索,才能总结升华知识,提高自己的认知水平,发现数学蕴藏的更多对称美及规律,以下简单介绍两种二项式展开式的系数规律的表现形式:
1.第n行上数字组成的数是11n
n=1 1 1→111=11
n=2 1 2 1→112=121
n=3 1 3 3 1→113=1331
n=4 1 4 6 4 1→114=14641
n=5 1 5 10 10 5 1→115=161051
n=6 1 6 15 20 15 6 1→116=1771561
……
解析:前4行的数字只要自己数字放在自己的数位就可以了,比如当n=4时,个位数是1,十位数是4,百位数是6,千位数是4,万位数是1,组合起来是14641,则114=14641;而从第5行开始有的数位就出现两位数,此时的两位数要采取进位的办法,以n=5为例,百位数是10,保留0,1进位到千位数去;千位数本来也是10,由于百位数进1后此时变成11,则保留个位的1,另十位的1进位到萬位数去;万位数本来是5,此时变为6;十万位数还是1;则数字变为161051,即为115。
2.第n行数字相加的和就是2n
n=1 1+1 21=2
n=2 1+2+1 22=4
n=3 1+3+3+1 23=8
n=4 1+4+6+4+1 24=16
n=5 1+5+10+10+5+1 25=32
n=6 1+6+15+20+15+6+1 26=64
……
通过观察学生会发现该数列背后存在如此美的规律,形式上是如此的对称,从而让中职学生不再感觉学习数学是那么的可怕。在引导学生认识对称美时,教师要注意在生活实践中的对称一般是以几何形态存在,所以,学生认识具体图形的对称美是比较容易的。但是对代数式方面的数学对称要观察和理解起来就不是那么容易了,这就要求教师在引导这方面的认识要加强,避免学生存在认识的误区,也就是说数学对称美不局限在几何图形上面。
(三)定理的对称美
数学的对称美常体现在数学中各种定理之间的对称。比如:两直线平行的判定:“同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行。”两直线平行的性质:“两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补。”这些就是数学定理之间存在对称关系的完美诠释。从数字运算的角度来看:加与减、乘与除、开方与乘方、指数与对数等,这些虽然是互逆的运算,也都可视为对称的关系。
三、对称美在日常中职数学教学中的巧用及案例分析
(一)代数式求最值问题
解决这类问题,用常规的方法难度和计算量都较大,一般通过观察构造,利用对称思想,也许可以取得事半功倍的效果。
例如:已知a,b∈R+,a+b=10,求ab的最大值。
分析:此题的常规解法要涉及二次代数式的配方问题,而配方几乎是所有中职学生的薄弱点,所以如果运用对称思维,构造对称,如由a+b=10,令a=5+x,b=5-x,则ab=(5+x)(5-x)=25-x2,故显然可以得出当x=0时,即a=b=5时ab取最大值,且最大值为25。
(二)解不等式问题
解含绝对值符号的一元一次不等式是中职学业水平测试的必考内容之一,也是教学的难点,很多中职学生在解题过程中经常跟一元二次不等式的解法混淆在一起。
例如:解不等式|2x-3|<5。
分析:利用初中绝对值对称美的性质,先由|x|=5的根为x=-5或5,引出|x|<5的解为-5
(三)利用几何对称求最值问题
(四)函数奇偶性的判断问题
函数奇偶性的判断在中职学业水平测试中通常出现的考题是在选择题或填空题上。如果用解答题的思路,用定义理论去推导证明函数的奇偶性,计算量大且容易出错,我们怕学生难以做到。故此问题如果用对称美的思维,也许就简单多了。本身函数要有奇偶性的前提条件定义域就必须关于原点对称,则可以利用这一对称特性,在定义域中取任意一对相反数代入函数解析式求出函数值,然后通过函数值的结果就可以直接判断函数的奇偶性,具体结论如下:(1)当函数值相等时,原函数为偶函数;(2)当函数值为相反数时,原函数为奇函数;(3)当函数值不相等也不是相反数时,原函数为非奇非偶函数。
例如:判断函数f(x)=3x2+|x|+1的奇偶性。
分析:该题的定义域为x∈(-∞,+∞),根据对称美可以在定义域内任意取一对简单的相反数,如取x=-1和1,把它们分别代入原函数中去求函数值,则f(-1)=3×(-1)2+|-1|+1=5,f(1)=3×(1)2+|1|+1=5,所以所得的函数值结果都是5,根据以上的结论,直接可得原函数为偶函数。用这样的办法简单明了且效果好。
(五)数列运算问题
对称美在数列中经常使用到,比如等差数列的性质am+an=ap+aq(m+n=p+q)和等比数列的性质aman=apaq(m+n=p+q)就是对称美的体现。等差数列的前n项和的运用也可以利用对称美来解决。
例如:求1+3+5+……+(2n-1)的值。
分析:此题是等差数列的前n项和的运算,在还没有学习前n项和公式的情况下,一般利用对称美的思想解题会比较简单且容易让学生接受。假设x=1+3+5+…+(2n-3)+(2n-1) …①,利用对称性,同样也可写成x=(2n-1)+(2n-3)+(2n-5)+…+5+3+1…②,由①+②得2x=[1+(2n-1)]+[3+(2n-3)]+[5+(2n-5)]+…+[(2n-3)+3]+[(2n-1)+1]=2n·n=2n2,∴x=n2,即1+3+5+…+(2n-1)的值为n2。
利用等差数列的性质am+an=ap+aq (m+n=p+q)来解题是常用的,而且方便、快捷。
又如:已知等差数列a4=10,a17=20,则求S20的值。
四、总结与思考
数学对称美是很多数学家一直以来追求的方向,本文结合自身的一线教学经验及参考文献,以中职数学课程为载体,分析对称美在中职数学教学中的巧用,主要通过对称美的具体案例进行阐述。中职数学更需要对数学对称美这方面的培养,引导学生利用对称思维来理解数学。合理运用数学对称美来加深对数学的认知,加深对数学思想的渗透,从而达到高效、快捷地寻求解题思路。同时,利用数学对称美让中职学生提高他们的审美眼光和素质,使中职数学课堂不再枯燥无味。
总之,随着国家对中等职业学校数学学科新课标的制定和我省学业水平测试的推动下,在中职数学教学中推进美育会随之越来越受到重视。通过数学对称美的思想来吸引、激发学生的数学兴趣,从而引导学生独立观察问题、发现问题、分析问题、解决问题。利用数学对称美解二次函数的解析式、直线和圆的方程、概率、简单几何体、指数函数和对数函数等各个领域都可以应用到,由于笔者才疏学浅,案例分析无法面面俱到,还需要加强深层次的研究,同时也希望更多同行在教学上应予以高度重视,深入研究中职数学的对称美在具体教学中的巧用,让更多师生受益。
参考文献:
[1]张奠基,木振武.数学美与数学教学中的审美[J].山东教育,1997(5).
[2]国务院办公厅.关于全面加强和改进学校美育工作的意见[Z],2015-09.
[3]唐瑞芬,朱成杰.数学教学理论选讲[M].上海:华东师范大学出版社,2011.
[4]李玉琪.中学数学教学与实践研究[M].北京:高等教育出版社,2010.
[5]胡雄伟.数学强化训练[M].北京:中央民族大学出版社,2014.
[6]余文森.课堂教学实施素质教育的“四个基本点”[J].教育研究,1997(9).
◎编辑 鲁翠红
