基于接触的轨道运输车升降系统传动结构稳定性分析
2021-01-08普江华王学军陈明方
普江华,王学军,吴 鹏,陈明方,杨 雄
(昆明理工大学 机电工程学院,云南 昆明 650500)
轨道运输车是广泛应用于铁路、冶金、矿山等领域的一种重要辅助设备。轨道运输车利用升降机构实现货物的转移,既节省人力又提高工作效率,故对轨道运输车升降机构进行研究具有重要的实际意义。图1中为该型轨道运输车用于铜电解加工时的场景,其作用为将前置设备输送过来的整齐排列的粗镍板从输送链上提升一定高度,然后水平输送到电解车间的另一工作区域[1]。其中,镍板提升通过轨道运输车升降系统完成。升降系统提升过程的不稳定性导致轨道运输车工作效率低、可靠性差。为了提高轨道运输车的运输质量和效率,必须提高其升降过程中的稳定性[2-3]。
蜗杆传动机构作为升降系统的主要传动部件,具有传动比大、噪声低、结构紧凑等优点[4]。对于蜗杆传动的建模与动力学研究,Bodzás S[5]等设计了一种轴截面上具有弓形齿廓的新型圆锥蜗杆传动方式,通过有限元分析比较得出,轴截面为弧形齿廓的蜗杆传动形式比轴截面为线性齿廓的蜗杆传动形式具有更好的应力、应变和变形值。Simon V[6]采用双圆弧型砂轮对蜗杆进行磨削,研制了一种新型圆柱蜗杆传动,并开发了一种新型蜗杆传动应力分析的有限元方法和相应的计算机程序。Zhao Y[7]等系统地建立了改进型弧面蜗杆传动的啮合几何模型,并建立蜗杆副啮合分析的数学模型,对改进后的传动装置的啮合特性进行了仿真研究。Sohn J[8]等提出了将蜗轮纵向凸度由不对称改为对称的修正方法,并用表面分离拓扑和接触压力对其进行分析,从而验证修正方法的正确性。Sobek M[9]介绍了一种通过测试齿轮运行过程中的扭矩变化来确定两个蜗杆传动装置轴间适当距离的试验方法。Polyakov S A[10]等研究了蜗杆传动中自激摩擦振动的产生及其与齿轮性能特性的相互关系,并基于所得到的关系式,提出了一种蜗轮加速试验方法。Ke L I[11]等基于多体动力学理论和有限元方法对蜗杆传动系统的疲劳寿命进行了预测。目前,对于蜗杆传动直接在CAD软件进行自动三维模型建立的研究与动力学分析的文献相对较少。对于蜗杆传动特性多用有限元方法进行分析,无法有效说明蜗杆传动的动态特性,对蜗轮蜗杆传动过程的动力学特性分析也缺乏参考方法。蜗杆传动是影响轨道运输车升降系统使用性能的主要因素,研究蜗杆传动机构的啮合过程是分析稳定性的关键。因此,研究蜗轮蜗杆啮合的动力学特性,不但为蜗杆蜗轮传动的动力学建模与分析提供了理论参考,也对升降系统传动结构的稳定性研究有着非常重要的现实意义。
本文通过多体动力学理论及Hertz接触理论建立轨道运输车升降系统传动结构动力学模型,对传动结构中蜗轮蜗杆的啮合过程进行分析,探寻蜗轮蜗杆之间接触力的变化规律,从而找到造成升降结构不稳定的主要原因。本文还对影响升降系统传动结构稳定性的因素进行分析,为提高轨道运输车升降系统的可靠性、高效性和蜗轮蜗杆传动的动力学特性研究提供了理论参考。
1 轨道运输车升降系统的三维实体建模
1.1 轨道运输车升降系统三维模型
轨道运输车是一种广泛应用于铁路、冶金、矿山等领域的有轨输送设备。轨道运输车升降系统传动关系简图如图2所示。根据图2可分析出其具体工作过程如下:升降电机驱动大直齿圆锥齿轮,并通过小直齿圆锥齿轮将运动传递到旋转轴I和另两对啮合的大直齿圆锥齿轮和小直齿圆锥齿轮;两对啮合的大直齿圆锥齿轮和小直齿圆锥齿轮将运动传递到位于两侧的旋转轴II;旋转轴II旋转带动4个蜗杆和4个蜗轮转动,蜗轮蜗杆机构将旋转运动转换为四对丝杆升降机构的上下直线运动,从而完成了铜阳极板的提取任务。其中,丝杠升降机构位置如图3所示。
为了方便分析轨道运输车升降过程,对轨道运输车升降系统部分细节进行了适当简化,并利用三维实体设计软件,完成轨道运输车升降系统的锥齿轮、蜗轮蜗杆、丝杆、丝杆螺母、联轴器、传动轴、机架、升降电机等的建模。经过装配,得到了轨道运车升降系统的装配模型,如图3所示。布置在机架四个角落的丝杠升降机构要实现同步升降,使物件在提升过程中能保持平稳,防止物件在运输过程中发生反转,同时采用大直齿圆锥齿轮和小直齿圆锥齿轮啮合,改善了传动稳定性和传动效率。

图2 传动系统简图Figure 2. Schematic diagram of transmission system
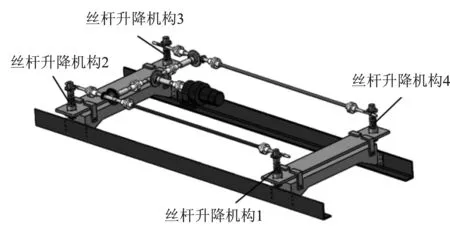
图3 轨道运输车升降系统Figure 3. Lifting system of rail transport conveyor
1.2 蜗轮蜗杆设计参数和三维模型
蜗杆传动机构作为升降系统的主要传动部件,是影响轨道运输车升降系统使用性能的主要因素。蜗杆传动机构如图4所示,蜗轮、蜗杆的结构参数如表1和表2所示。
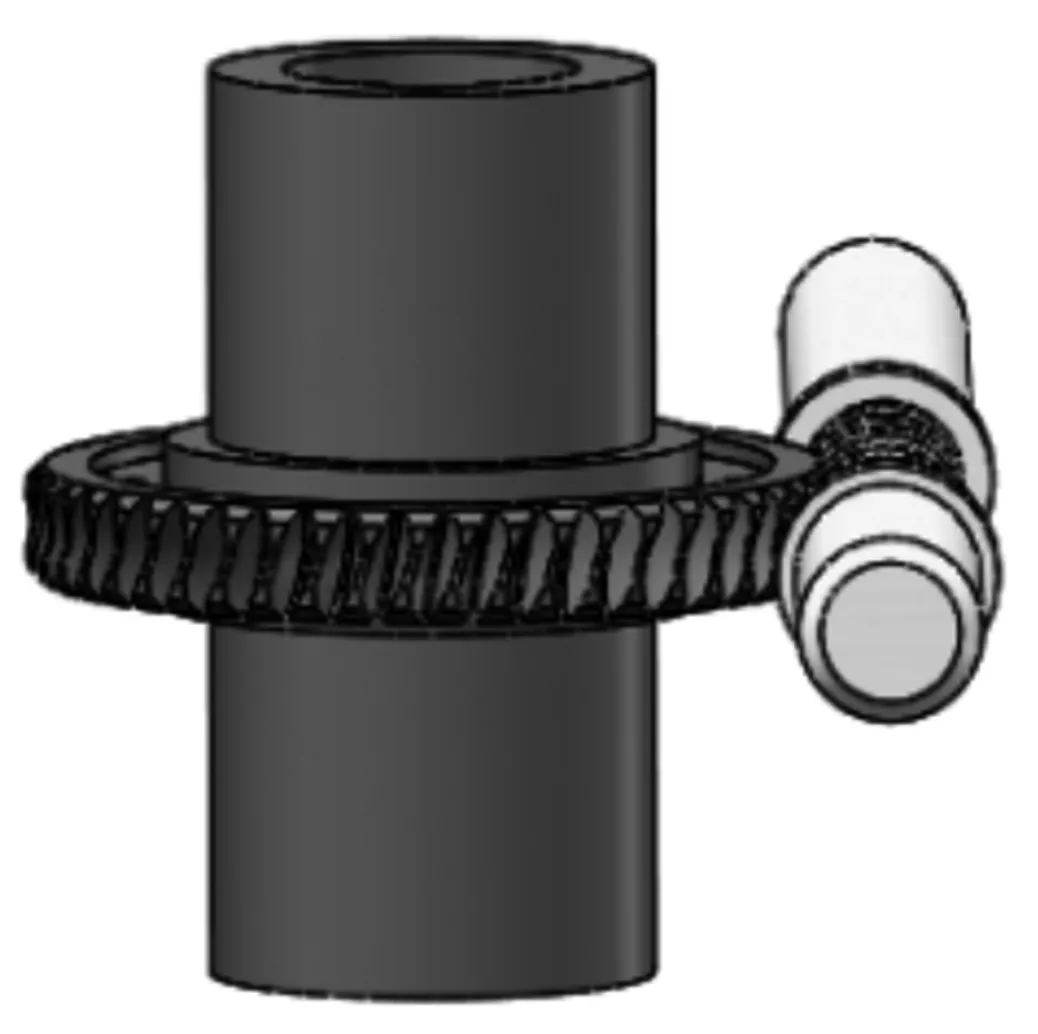
图4 蜗杆传动机构Figure 4. Worm drive mechanism

表1 蜗轮结构参数

表2 蜗杆结构参数
2 轨道运输车升降系统传动结构的动力学建模
2.1 动力学方程
采用欧拉-拉格朗日方法对传动模型进行求解。根据机械系统模型,建立轨道运输车升降系统传动结构的拉格朗日运动方程,列出对应于6个广义坐标带乘子的拉格朗日方程,即需要的约束方程[12-13]
(1)
式中,i=1,…,n;j=1,…,m;k为系统的动能;qj为描述系统的广义坐标;Φi为系统的约束方程;Fj为广义坐标上的广义力;λi为拉式乘子。
2.2 蜗轮蜗杆接触力计算法
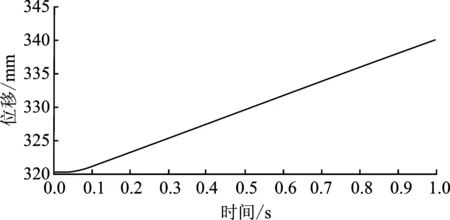
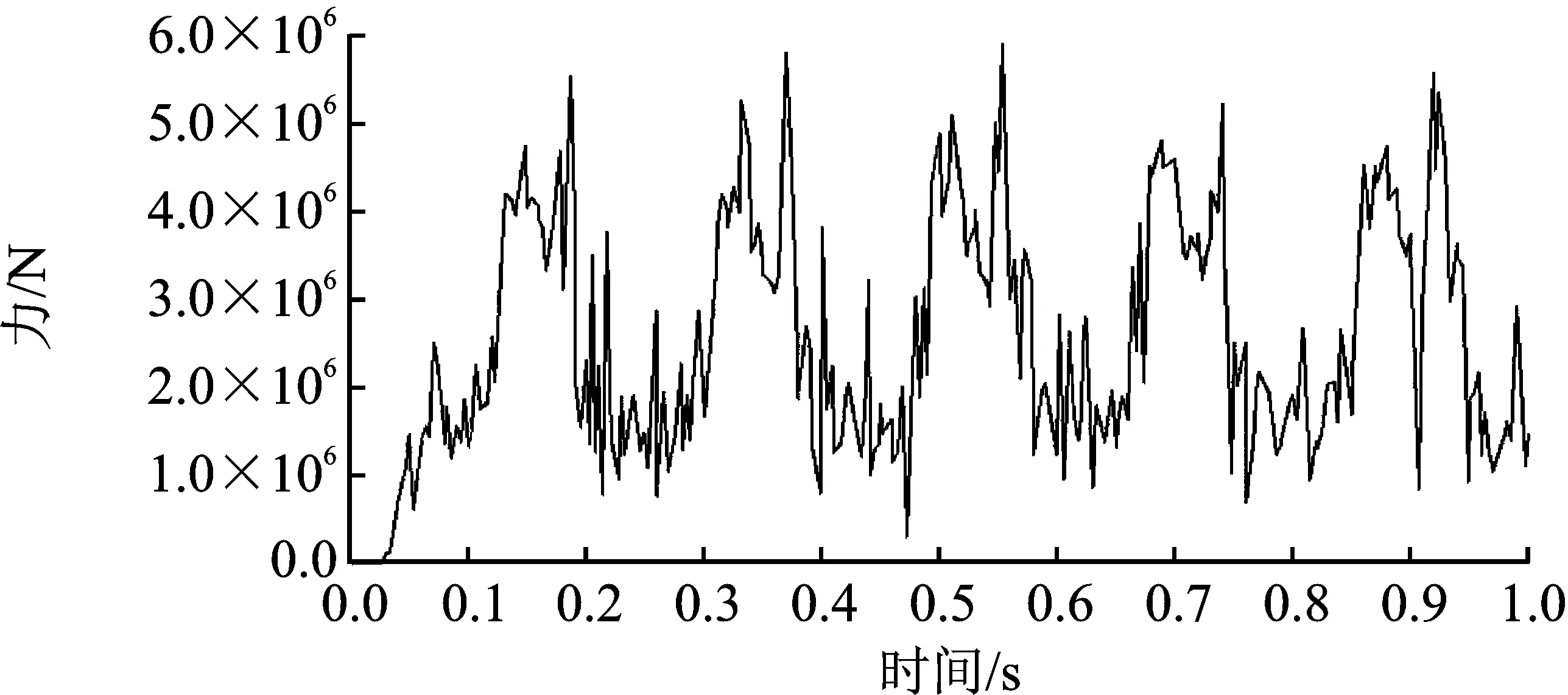
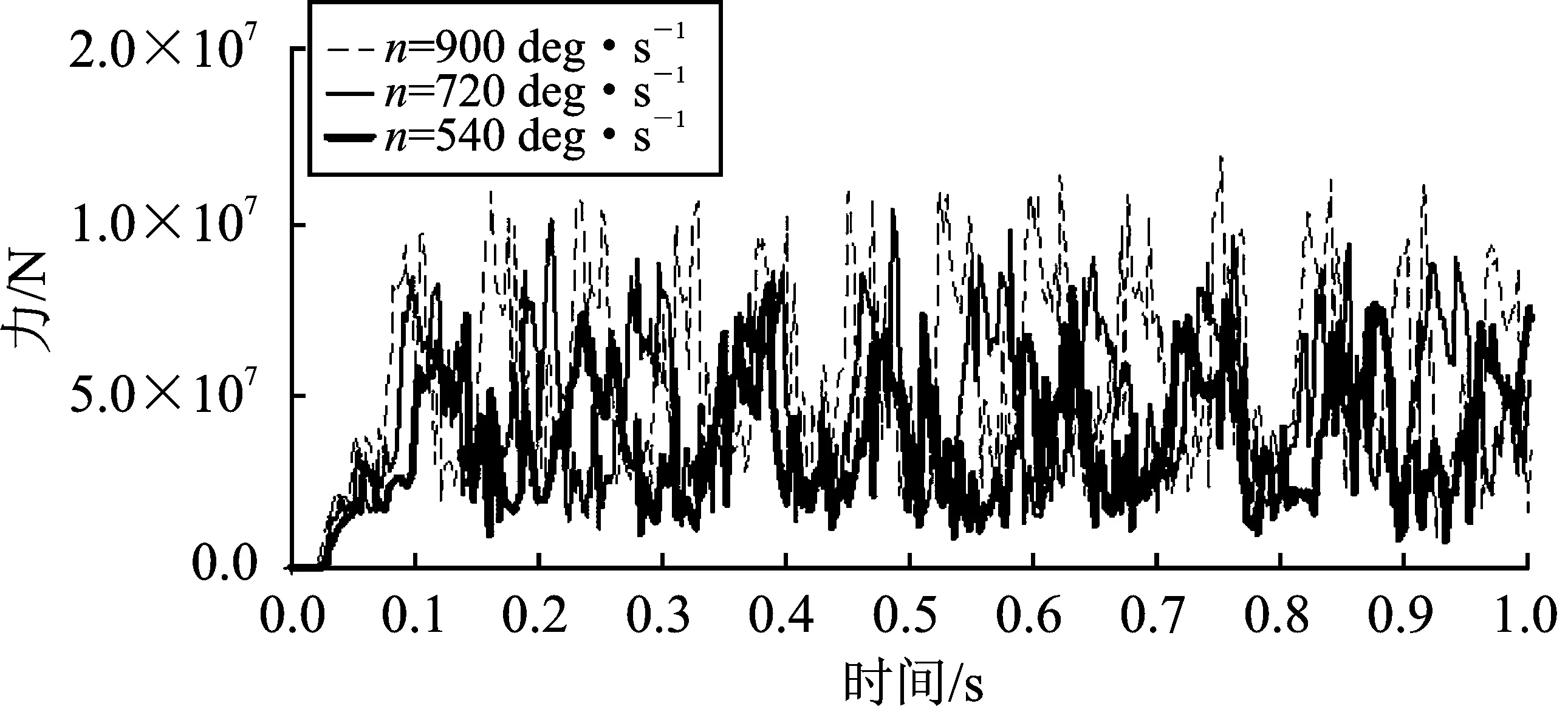
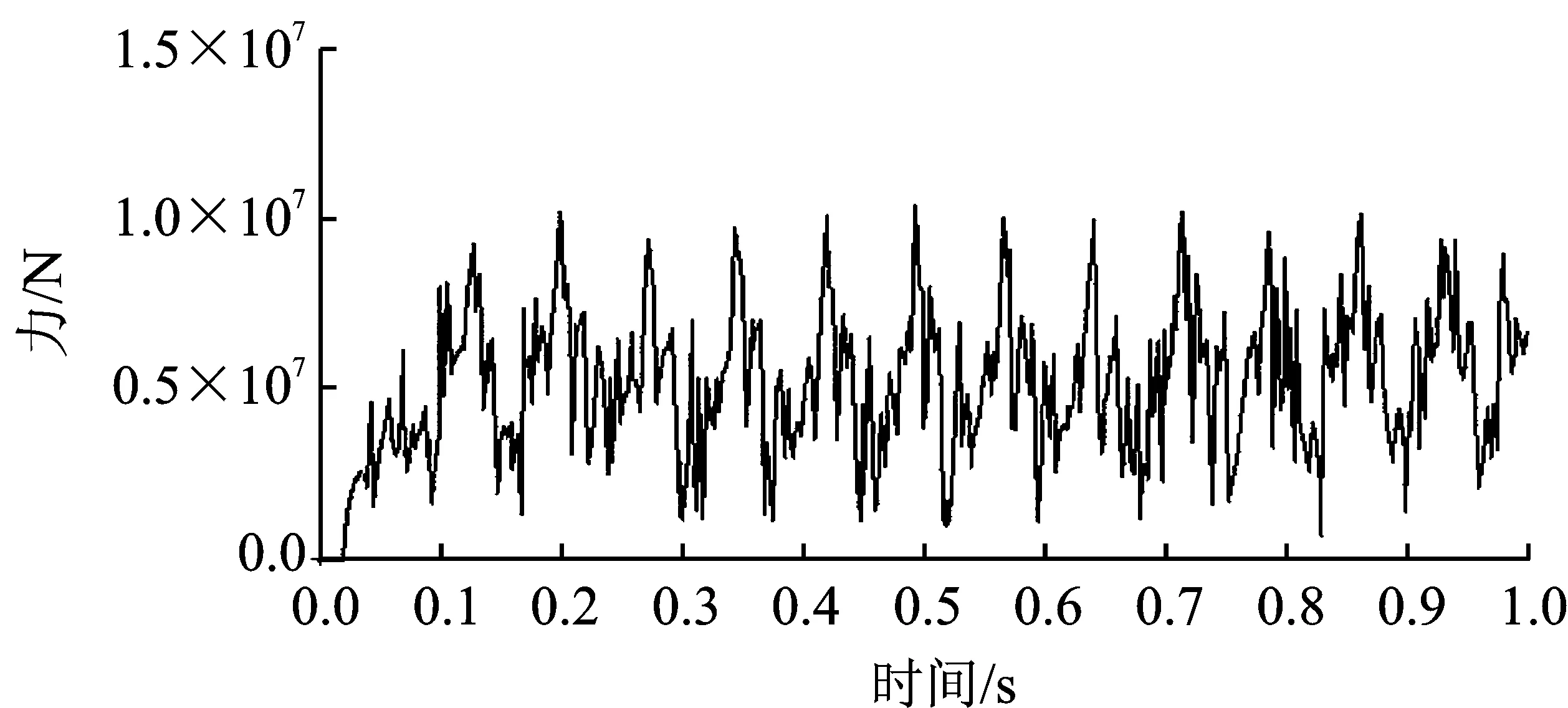
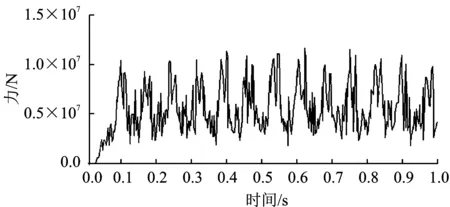
蜗轮蜗杆在啮合过程中,因接触产生接触力。对相互接触的蜗轮蜗杆,设q0为蜗轮蜗杆要碰撞的初始距离,q为蜗轮蜗杆碰撞时的实际距离。分析时忽略蜗轮蜗杆的弹性波动和运动副间隙,当q0≥q时,蜗轮蜗杆不发生接触,接触力为0 kN;当q0 F= (2) 式中,k为啮合刚度;e为非线性指数;cmax为最大阻尼系数;fs为step函数;d为穿入深度。 (3) 为了防止碰撞过程中阻尼力不连续,式中采用了step函数,其形式为step(x,x0,h0,x1,h1),其定义如下 (4) 式中,a=h1-h0;Δ=(x-x0)/(x1-x0);x为函数自变量;x0、h0、x1、h1均为实数;x0为step函数自变量的初始值;h0为step函数的初始值;x1为step函数结束时自变量值;h1为step函数结束时的函数值。 蜗杆蜗轮材料分别取为ZCuAl10Fe3和45钢,则E1=109.8 GPa,E2=210 GPa;μ1=0.335,μ2=0.269。接触处R1=130 mm,R2=18 mm。根据式(2)~式(4)可得蜗轮蜗杆碰撞的刚度系数k=4.23×105N·mm-1,阻尼系数为刚度系数的0.1%~1%,碰撞指数取2.2,穿透深度取0.1 mm,动摩擦系数取0.1,静摩擦系数取0.3[17]。 对简化的轨道运输车升降系统的三维几何模型施加运动学约束、驱动约束和力等物理要素,得到表达系统力学特性的物理模型模拟轨道运输车升降过程,如图5所示。 图5 轨道运输车虚拟样机模型Figure 5. Virtual prototype model of rail transport conveyor 基于多体动力学理论和Hertz接触理论对轨道运输车升降过程进行分析。为了避免圆锥齿轮和蜗轮蜗杆首次接触碰撞引起速度突变,分析时转速以阶跃函数形式添加,为step(time,0,0d,1,360d)[18]。计算时间取为1 s进行分析,得到系统的特性曲线,如图6~图9所示。 图6为蜗轮和蜗杆转速曲线。由图6可知当升降电机输出转速为360 deg·s-1时,经过锥齿轮传动,使蜗杆平均值转速为1 960.15 deg·s-1,蜗轮平均值转速为75.46 deg·s-1,并且蜗轮蜗杆转速值以一定幅值波动。由于蜗轮蜗杆传动比可知,蜗轮的理论转速为75.39 deg·s-1。分析值与理论值相对误差为0.093%,分析数据满足传动比要求,证明了分析模型和分析过程的正确性。 图6 蜗轮蜗杆转速Figure 6. Worm gear and worm speed 图7为布置在机架4个角落的丝杠升降机构行程曲线,其中图7(a)为丝杆升降机构1的行程曲线;图7(b)为丝杆升降机构2的行程曲线;图7(c)为丝杆升降机构3的行程曲线;图7(d)为丝杆升降机构4的行程曲线。由图7可知,文中4个升降机构在1 s内上升高度分别为19.867 4 mm、19.776 1 mm、19.861 6 mm和19.781 9 mm,上升高度基本相同。所得上升高度差最值为0.091 3 mm,在0.1 mm以内满足工作要求,说明轨道运输车不同位置处的丝杠升降机构能实现同步升降。 (a) (b) (c) (d)图7 升降系统行程曲线(a)丝杆升降机构1的行程曲线 (b)丝杆升降机构2的行程曲线 (c)丝杆升降机构3的行程曲线 (d)丝杆升降机构4的行程曲线Figure 7. Stroke curve of lifting system(a) Stroke curve of screw lifting mechanism 1 (b) Stroke curve of screw lifting mechanism 2 (c) Stroke curve of screw lifting mechanism 3 (d) Stroke curve of screw lifting mechanism 4 但由图8丝杠升降机构4的速度曲线可知轨道运输车在上升过程中,其速度是不断变化的,且这种变化是非线性的。因此丝杠升降机构在升降过程中会产生柔性冲击,从而影响轨道运输车升降系统的稳定性。 图8 丝杠升降机构速度曲线Figure 8. Speed curve of screw lifting mechanism 图9为蜗杆传动机构接触力,由于蜗轮蜗杆在传动过程中产生碰撞冲击,从而导致接触力在均值2.81×106N,附近上下波动。接触力的这种周期性波动不仅容易造成蜗杆传动机构的疲劳破坏,而且会引起很大的振动和冲击,导致升降机构在升降过程中会产柔性冲击,影响升降系统的稳定性。 图9 蜗杆传动机构的接触力Figure 9. Contact force of worm drive mechanism 综上可得,轨道运输车能实现同步提升,但在提升过程中蜗杆传动机构的接触力呈周期性波动使得丝杆升降机构的速度不断变化。因此接触力的周期性波动使升降系统传动结构产生柔性冲击,是影响升降系统稳定性的主要原因,同时可以通过降低接触力的大小和波动幅度来提高升降系统的稳定性。 3.2.1 刚度系数影响分析 为研究刚度系数对升降系统稳定性的影响,在输入速度和外载荷等都相同的情况下,刚度系数为2.0×105N·mm-2、4.0×105N·mm-2和6.0×105N·mm-2时得到接触力变化曲线如图10所示。 图10 在不同刚都系数下的接触力Figure 10. Contact force under different stiffness coefficients 由图10可得,当K=2.0×105N·mm-2时,接触力均值在7.64×105N附近波动,最大值为2.0×106N,最小值为4.42×103N;当K=4.0×105N·mm-2时,接触力均值在3.80×106N附近波动,最大值为8.67×106N,最小值为8.72×103N;最后,当K=6.0×105N·mm-2时,接触力的均值在8.64×106N附近上下波动,最大值为1.92×107N,最小值为1.40×104N。该结果说明,由于蜗轮蜗杆自身结构原因,在不同刚度系数下其接触力呈周期变化,并且接触力的大小和波动幅度随着刚系数的增大而增大,即刚度系数越大升降系统越不稳定。同时接触力均值的相对增长量随着刚度系数增大而增大,说明刚度系数是影响轨道运输车升降系统传动结构稳定性的重要因素。 3.2.2 电机驱动速度影响分析 为研究电机驱动速度对升降系统稳定性的影响,在刚度系数和外载荷等都相同的情况下,分别取转速为540 deg·s-1、720 deg·s-1和900 deg·s-1,得到接触力变化曲线如图11所示。 图11 在不同转速下的接触力Figure 11. Contact force at different rotational speeds 由图11可得,当n=540 deg·s-1时,接触力均值在3.83×106N附近波动,最大值为8.73×106N,最小值为2.18×103N;当n=720 deg·s-1时,接触力均值在4.84×106N附近波动,最大值为1.04×107N,最小值为9.80×103N;当n=900 deg·s-1时,接触力均值在5.90×106N附近上下波动,最大值为1.26×107N,最小值为9.41×103N。该结果说明,由于蜗轮蜗杆自身结构原因,在不同转速下其接触力呈周期变化,并且接触力大小和波动幅度随着转速的增大而增大,即转速越大升降系统越不稳定。 3.2.3 传动距离影响分析 动力传动距离是影响升降系统稳定性的因素,当转速为900 deg·s-1,刚度系数为4.24×105N·mm-2时,距离升降电机较近一侧的蜗杆传动机构接触力如图12所示,距离升降电机较远一侧的蜗杆传动机构接触力如图13所示。 图12 传动距离近一侧蜗杆传动机构接触力Figure 12. Contact force of worm drive mechanism near the side of lifting motor 图13 传动距离远一侧蜗杆传动机构接触力Figure 13. Contact force of worm drive mechanism far from the side of lifting motor 由图12可得接触力的均值在5.16×106N附近上下波动,最大值为1.15×107N,最小值为1.02×104N。由图13可得接触力的均值在5.82×106N附近上下波动,最大值为1.20×107N,最小值为9.38×103N。结果表明传动距离越远,接触力越大,波动幅度越大,升降系统越不稳定。 本文建立了轨道运输车升降系统的三维模型,并通过多体动力学理论及Hertz接触理论对轨道运输车升降传动结构进行动力学建模。对轨道运输车升降传动结构中蜗轮蜗杆的啮合过程进行分析,为蜗轮蜗杆传动的动力学特性研究提供了一种参考方法。 通过对传动结构中蜗轮蜗杆传动机构的接触力变化规律进行研究,发现接触时瞬时冲击及接触力的周期性波动是造成升降系统传动结构不稳定的主要原因。得出可以通过减低接触力的大小和波动幅度来提高升降系统的稳定性。 本文对刚度系数、电机驱动速度及传动距离对传动系统稳定性影响进行分析。得出接触力的大小和波动幅度随着刚系数、升降电机转速和传动距离的增大而增大,刚度系数、升降电机转速越和传动距离越大升降系统越不稳定。为轨道运输车新型传动结构的设计提供了理论依据。

3 轨道运输车升降系统传动结构稳定性分析
3.1 轨道运输车升降过程分析



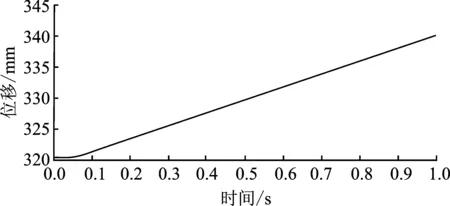
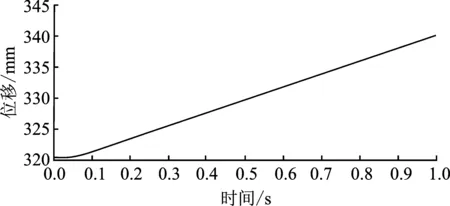

3.2 轨道运输车升降系统传动结构稳定性影响因素分析

4 结束语
