有限差分算法在导波模式可视化教学中的应用*
2021-01-08李继军
李继军,肖 循
(长江大学物理科学与光电工程学院,湖北 荆州 434023)
《电磁场与电磁波》是光电类专业的一门专业基础课程,课程具有数学知识较多,理论推导复杂,物理概念抽象等特点.课程教学难度较大,学生难以深刻理解知识的内涵.可视化教学是一种重要的提高教学效果的技术,但是部分文献[1~5]表明,这种可视化是对解析结果的绘图,并不能让学生对物理现象中所蕴涵的规律有深刻的理解.本文以波导模式分析为例,从最基本的麦克斯韦旋度方程出发,引入有限差分算法将其中的物理规律可视化.这种处理方式避免了复杂的数学公式推导,更利于学生对物理本质规律的理解.
1 有限差分算法的原理
有限差分法[6]的基本思想是把连续的定解区域用有限个离散点构成的网格来代替,这些离散点称为网格的节点.将连续定解区域上的连续变量函数用在网格上定义的离散变量函数来近似,将原方程和定解条件中的微商用差商来近似,于是原微分方程和定解条件将近似的表示为代数方程组,即有限差分方程组.解此方程组就可以得到原问题在离散点上的近似解,然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解.
2 导波模式矩阵方程的推导
假设波函数与时间相关的因子为exp(-jωt),则频域麦克斯韦旋度方程[7]为:
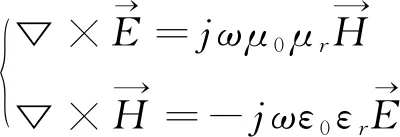
(1)

则旋度方程变化为:


设二维平板介质波导结构如图1所示,电磁波沿z轴传播,在x轴方向受到限制,深灰色所示的波导芯层厚度为t,波导在垂直纸面向外的y轴方向上无限大且均匀.

图1 波导结构
在该波导结构中,矢量旋度方程可以演变为E模式和H模式方程组.
E模式方程组为:
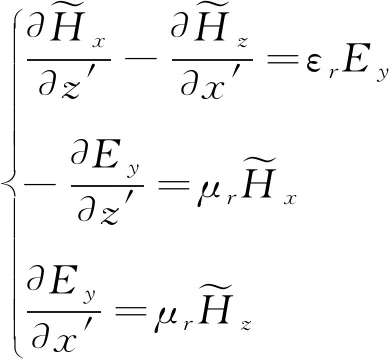
(2)
H模式方程组为:
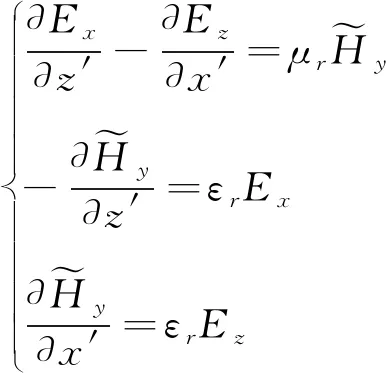
(3)
式中x′=k0x,y′=k0y,z′=k0z
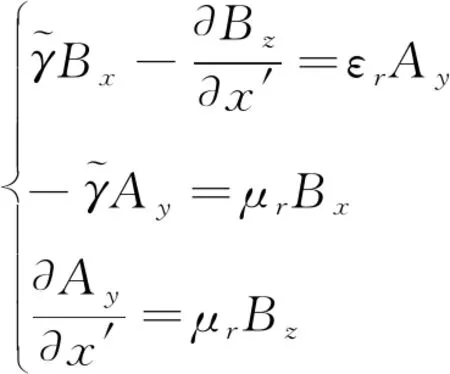
(4)

(5)
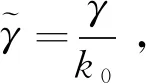
为了求解(4)、(5)式,需要将求解区域分割成离散的网格.根据有限差分法原理,(4)、(5)式就变成由网格数来决定方程数量的代数方程组, 其矩阵形式如下:
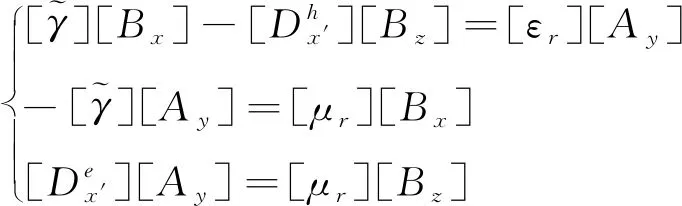
(6)

(7)

式中,Δx表示网格大小.
由(6)式中的第二和第三个式子解出[Bx]、[Bz],并将其代入第一个式子,得到E模的本征方程:
(8)
同理,由(7)式可以推导出H模式的本征方程:
(9)
因此,求解受麦克斯韦方程组和边界条件约束的导波解,通过数学变换,最终转化为求解(8)、(9)两个本征方程.
3 导波模式可视化的Matlab实现
采用Matlab对一个实际问题[10]进行编程.假设平板波导是一个对称包覆介质波导,芯层厚度为4微米,折射率n1=1.568,包层折射率n2=1.538,入射光波长为0.632 8微米.
3.1 初始化参数
% matlab初始化
close all;
clc;
clear all;
um = 1e-6; %以微米作为坐标轴单位
lam0 = 0.6328 * um; %入射光波长
k0 = 2 * pi / lam0; %入射光波矢
n1 = 1.568; %波导芯层折射率
n2 = 1.538; %波导覆盖层折射率
n3 = n2; %波导衬底层折射率
t = 4 * um; %波导芯层厚度
b = 10 * um; %波导包覆层厚度
NRES = 50; %计算空间分辨率
dx = lam0/NRES; %计算空间网格尺度
M = 5; %导波模式数目
% 计算空间网格数
Sx = t + 2*b; %计算物理空间实际大小
Nx = ceil(Sx/dx);
Sx = Nx * dx;
xt = [0.5 : Nx-0.5]*dx;
xt = xt - mean(xt); %将x轴坐标原点放在波导对称中心
% 设置计算空间折射率分布
nx = round(t/dx); % 波导芯层网格数
nx1 = round((Nx - nx)/2); % 波导芯层下端的坐标
nx2 = nx1 + nx - 1; % 波导芯层上端的坐标
% 设置空间介电常数及磁导率矩阵;
% ER表示介质的介电常数
ER(1 : nx1-1) = n2^2;
ER(nx1 : nx2) = n1^2;
ER(nx2+1 : Nx) = n3^2;
ER=diag(sparse(ER(:)));
% MUR表示介质的磁导率
MUR(1:Nx) = 1.0;
MUR=diag(sparse(MUR(:)));
3.2 求导矩阵的设置
DEX = sparse(Nx,Nx); % DEX代表对电场分量的求导
d = ones(Nx,1);
DEX = spdiags(-d,0,DEX);
DEX = spdiags(d,+1,DEX);
DEX = DEX / dx;
DEX = DEX / k0; % 归一化后的求导矩阵
DHX = - ctranspose(DEX) ; % DHX代表对磁场分量的求导
3.3 特征方程的求解
% E模式分析
A_E = -( DHX/MUR*DEX + ER);
MUR_re(1 : Nx) = 1.0; % 介质磁导率的导数
B_E = diag(sparse(MUR_re(:))); % 介质磁导率的导数矩阵
[V_E, D_E] = eig(full(A_E),full(B_E)); % 求解特征值和特征矢量
NEFF_E = sqrt(diag(-D_E)); % 计算E模式等效折射率
% H模式分析
A_H = -( DEX/ER*DHX + MUR);
ER_re(1 : nx1-1) = 1/n2^2; % 介质介电常数的导数
ER_re(nx1 : nx2) = 1/n1^2;
ER_re(nx2+1 : Nx) = 1/ n2^2;
B_H = diag(sparse(ER_re(:))); % 介质介电常数的导数矩阵
[V_H,D_H] = eig(full(A_H),full(B_H)); % 求解特征值和特征矢量
NEFF_H = sqrt(diag(-D_H)); % 计算H模式等效折射率
3.4 计算结果可视化
%绘制E模式
[NEFF_E, ind] = sort(real(NEFF_E), ′descend′);
V_E = V_E(: ,ind);
f1 = figure(1);
set(f1,′Color′,′w′)
hold on
% 绘制波导形状
x = [0 2*(M+1) 2*(M+1) 0 0 ];
y = [-b-t/2 -b-t/2 b+t/2 b+t/2 -b-t/2];
fill(x,y,0.9*[1 1 1]);
y = [-t/2 -t/2 t/2 t/2 -t/2];
fill(x,y,0.5*[1 1 1]);
%绘制E模式波场分布
for m =1 : M
x0 = 2 * m;
y0 = (t+b)/2;
x = x0 + 3 * V_E(: , m);
y = linspace(-b-t/2, b+t/2,Nx);
line(x, y,′color′,′w′,′linewidth′,4);
h = line(x, y,′color′,′b′,′linewidth′,2);
text(x0,y0,[′mode ′ num2str(m)],′rotation′,-90,...
′horizontalalignment′,′center′,′verticalalignment′,′bottom′);
text(x0,-y0,[′n_{eff}= ′, num2str(NEFF_E(m),′%7.5f′)],′rotation′,-90,...
′horizontalalignment′,′center′,′verticalalignment′,′bottom′);
end
% 绘制H模式
f2 = figure(2);
set(f1,′Color′,′w′)
hold on
% 绘制波导形状
x = [0 2*(M+1) 2*(M+1) 0 0 ];
y = [-b-t/2 -b-t/2 b+t/2 b+t/2 -b-t/2];
fill(x,y,0.9*[1 1 1]);
y = [-t/2 -t/2 t/2 t/2 -t/2];
fill(x,y,0.5*[1 1 1]);
%绘制H模式波场分布
for m =1 : M
x0 = 2 * m;
y0 = (t+b)/2;
x = x0 + 3* V_H(: , m);
y = linspace(-b-t/2, b+t/2,Nx);
line(x, y,′color′,′w′,′linewidth′,4);
h = line(x, y,′color′,′r′,′linewidth′,2);
text(x0,y0,[′mode ′ num2str(m)],′rotation′,-90,...
′horizontalalignment′,′center′,′verticalalignment′,′bottom′);
text(x0,-y0,[′n_{eff}= ′, num2str(NEFF_H(m),′%7.5f′)],′rotation′,-90,...
′horizontalalignment′,′center′,′verticalalignment′,′bottom′);
end
根据分析结果,在图2和图3中分别绘制出来的E模和H模场的分布.图2中的mode1至mode4分别对应导模TE0至TE3,图3中的mode1至mode4分别对应导模TM0至TM3,各模式等效折射率如图中所示.图中非常直观的表明电磁场的横向分布具有对称性或反对称性,这源于介电常数是对称分布的.电磁场幅值在波导芯层中呈现为余弦或正弦分布,而在芯层两侧的包层中具有指数衰减的形式,随着远离芯层,幅值趋近于零.包层中这种指数衰减的场称为倏逝场.倏逝场衰减的快慢取决于电磁波在波导包层中的波矢的横向分量,该分量越大,倏逝场衰减的就越快.该分量取决于等效折射率,等效折射率越小,该分量就越小.图2和图3清晰的表明了这种规律,可以看到,随着模式等效折射率的减小,倏逝场在包层中的穿透深度越来愈大,这也说明高阶模式有更多的能量泄漏到包层中.图2与图3中mode5的等效折射率小于包层的折射率,模式曲线在芯层中不再是余弦或正弦分布,其物理含义是电磁场能量不再被限制在波导芯层中.这些模式的能量通过芯层与包层的界面辐射到包层中去了,该模式被称作辐射模.上述结论与实际结果吻合.图示结果形象的表明了导模和辐射模的特征,其中导波横向模场是以驻波的形式存在的,而辐射模则没有,这种规律的直观性是公式所不能给予的.

图2 E模式模场分布 图3 H模式模场分布
4 结语
本文从基本的麦克斯韦方程出发,利用有限差分法对二维平板介质波导中的电磁场进行了分析,得到的结果直观明确并与物理规律相符合.这样做不仅为学生加深对物理知识的理解提供了帮助,有助于提高学生的学习积极性,也有助于教师丰富教学内容和提高课堂教学效果.
