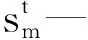厚壁圆筒强度及开孔补强的分析与讨论

张皓斌

华陆工程科技有限责任公司 西安 710065

在工程设计中，为处理问题方便通常将整体式圆筒分为厚壁筒和薄壁筒。一般将K=Do/Di≤1.2称为薄壁筒，将K=Do/Di>1.2称为厚壁筒。薄壁圆筒强度设计的理论基础是旋转薄壳的无力矩理论，因此计算的应力都是沿壁厚均匀分布的薄膜应力，且忽略了垂直于容器壁面的径向应力。由于薄壁圆筒的计算公式简单、计算方便，所以在工程中得到了大量的应用。同时为了解决部分厚壁筒体采用薄壁公式时引起的较大误差，采取增大计算内径，将圆筒计算中的内径修改为中径，扩大了公式的使用范围。经计算当K=1.5时，由中径公式计算的应力值与拉美公式环向最大应力(内壁处)的计算值相差仅3.8%，此误差在工程设计的允许范围内，所以我国的GB/T150.2-2011和JB4732-1995标准中给出的中径公式范围都是K小于等于1.5。

厚壁圆筒强度设计的理论基础是由弹性力学应力分析导出的拉美公式。根据拉美公式所求得的厚壁圆筒中的应力能够较好地与实际情况吻合，反应了应力的客观规律。我国的JB4732-1995标准对于K>1.5的厚壁圆筒设计则是按照Tresca全屈服压力准则进行设计。

同时，在压力容器上总有工艺管口和操作维修需要设置的人、手孔。由于开孔破坏了筒体结构的连续性，在开孔的边缘会产生很高的局部应力，为了降低开孔边缘的应力，必须在开孔的部位进行补强。目前，工程上常用的计算方法有等面积法、应力分类法、极限载荷法等。

下面通过实例对按照拉美公式和Tresca全屈服准则设计的筒体厚度进行分析，并对几种不同的开孔计算方法进行对比、分析。 (其中，符号说明详见文末。)

1 厚壁圆筒体的厚度设计

1.1 基于弹性失效准则的厚壁圆筒体厚度

厚壁圆筒体厚度计算的理论设计基础是由弹性力学分析导出的拉美公式，既适用于厚壁容器，也适用于薄壁容器。

(1)

1.2 基于塑性失效准则的厚壁圆筒体厚度

对于厚壁圆筒体，由于一般压力容器所用材料的塑性较好，当内壁材料屈服时，内壁面以外的材料仍处于弹性状态，故不会导致整个截面屈服，圆筒仍能继续承载。塑性失效准则认为：只有整个圆筒体沿厚度方向全部屈服时，筒体才算失效。

假设材料为理想弹塑性材料，按照Tresca全屈服失效准则，可得出内压圆筒能够承受的压力为Pe=[σ]tφlnK，相应的圆筒体厚度计算公式为：

(2)

2 常用的压力容器开孔补强方法对比、分析

压力容器的开孔补强是压力容器设计的重要环节。近些年来，随着石油化工、锅炉等行业中经常出现的高温、高压以及对装置大型化的要求，对设计提出了越来越苛刻的要求。特别是近些年来，随着计算机技术的快速发展，有限元分析技术在工业设计中得到了广泛的应用，从而推动了应力分类法以及极限载荷法在压力容器设计中的使用。通过分析设计方法可以解决很多等面积补强法无法解决的问题，得出更合理、更符合实际的结果。

2.1 等面积补强法

等面积补强法是以受拉伸的无限大平板上开小孔作为计算模型的一种开孔补强方法。以补偿开孔局部截面的拉伸强度作为补强准则的，其补强只涉及静力强度问题。对于孔边缘的二次应力安定性问题是通过限制开孔直径、开孔形状和开孔范围间接加以考虑的。所以我国的GB/T150.3-2011和JB4732-1995标准都对等面积补强法的使用范围有严格的规定。同时由于采用等面积补强法无法考虑接管的外载荷，建议采用其他计算方法进行确认。

2.2 应力分类法

应力分类法是基于线弹性分析，一般可通过有限元分析得到结构中的应力分布，此应力为名义应力，而不是结构中的真实应力分布。然后可对计算得到的名义应力进行线性化处理，在接管根部且垂直于壳体、接管壁厚的截面取路径，同时在过结构最大应力强度点的沿表面法线方向也取一条路径，进行线性化处理后，区分出薄膜应力、弯曲用力和峰值应力三类应力。根据JB4732-1995的规定，对以上应力按照相对应的许用极限进行评判，其中：SⅡ(PL)≤1.5Sm；SⅢ(PL+Pb)≤1.5Sm；SⅣ(PL+Pb+Q)≤3Sm。

2.3 极限载荷法

极限载荷是构件在外载荷作用下在整体上或某一局部的全厚度上由弹性状态进入塑性状态时所对应的载荷。进行极限载荷分析时须严格遵守极限载荷的两个基本假设：理想弹塑性材料和小变形理论。由于极限载荷法不考虑载荷变形过程和加载历史，只考虑结构在一次加载情况下的承载能力，因此JB4732-1995明确指出“若给定载荷不超过结构塑性极限载荷的2/3，则在结构具体部位上不需要满足一次总体薄膜应力SI、一次局部薄膜应力强度SII和一次薄膜加一次弯曲应力强度SIII的许用极限”，但还需要考虑二次应力所引起的塑性应变增加和疲劳破坏的影响。因此需要同时满足给定载荷下的一次加二次应力强度SIV≤3Sm，这样才能真正保证结构的安全性。

3 算例验证

3.1 厚壁圆筒体厚度计算算例

算例1：在某工程中，有一台高压储气罐，设备内径Di=1000 mm，设计压力Pc=68.8 MPa(G)，设计温度t=100℃，筒体材料为Q345R，在设计温度下材料的许用应力 [σ]t=167MPa，腐蚀余量C=0，焊接接头系数Ф=1.0。

3.1.1 按拉美公式进行圆筒体的强度计算

当圆筒体的厚度取275 mm时，可以由拉美公式计算出圆筒体内、外壁的结构应力值，见表1。

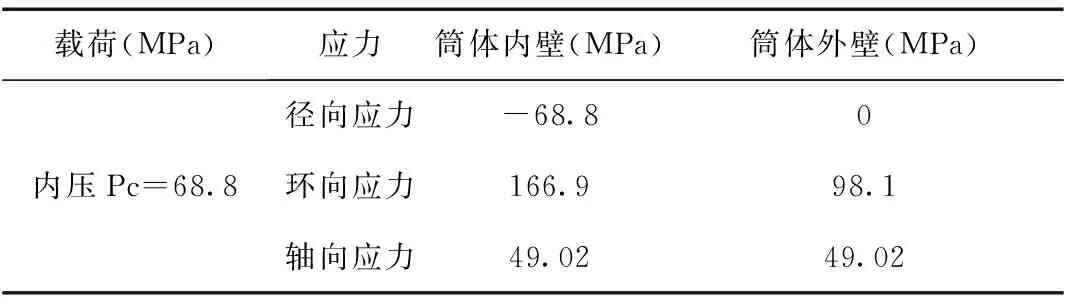
表1 拉美公式计算的圆筒体结构应力

同时采用目前比较流行的ANSYS软件进行有限元分析，计算出的圆筒体结构应力，见图1。

算例2：保持上述设备参数不变，只是将设计压力修改为Pc=90Mpa。

同样可以由式(1)计算出的圆筒体厚度为：

当圆筒体的厚度取414 mm时，可以由拉美公式计算出圆筒体内、外壁的结构应力值，见表2。

同样可以采用ANSYS软件进行有限元分析，计算出当圆筒体厚度为414 mm时，筒体内、外壁的结构应力见图2。

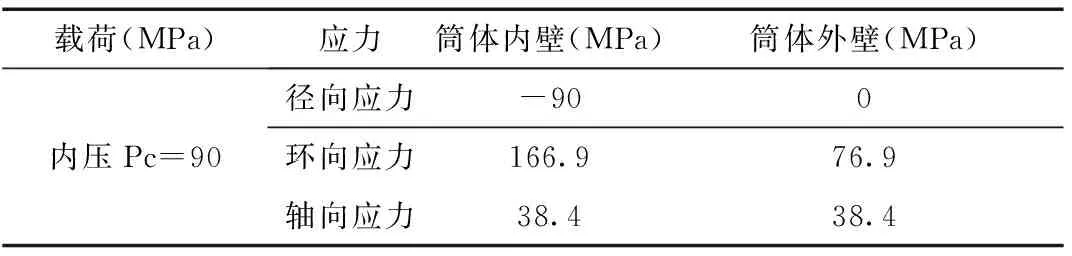
表2 拉美公式计算的圆筒体结构应力

图1 厚度275 mm圆筒体内、外壁结构应力

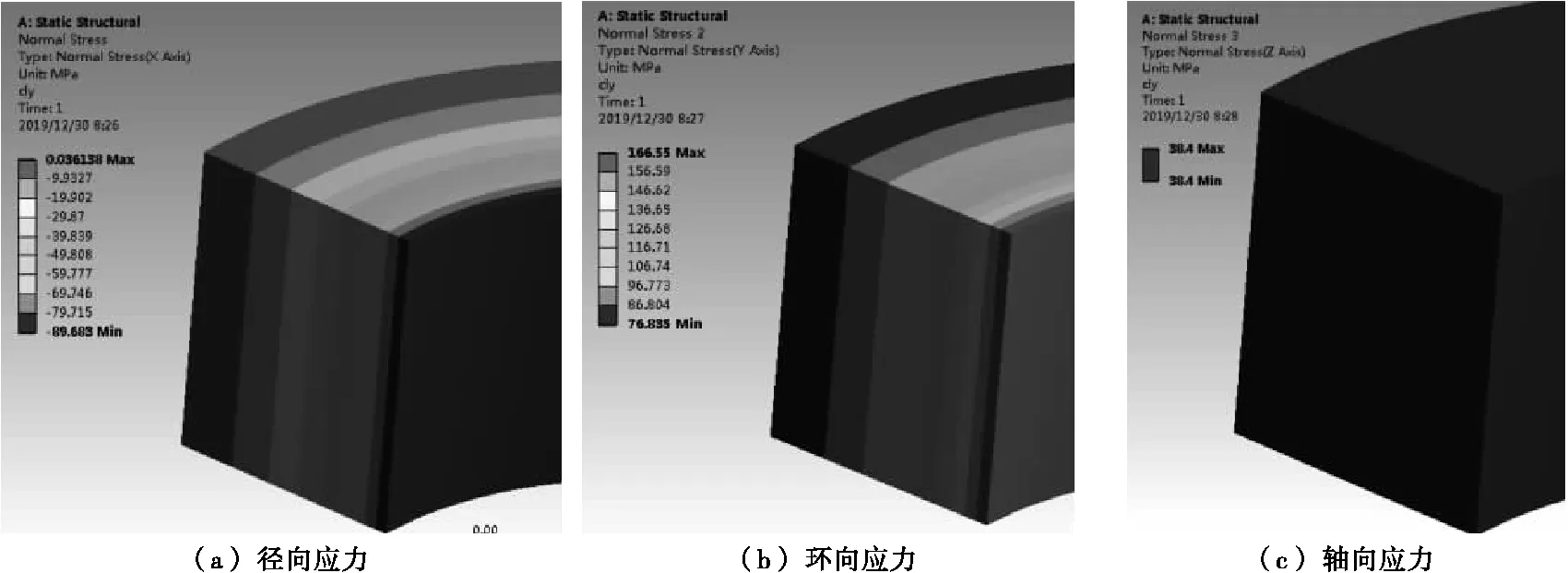
图2 厚度414 mm圆筒体内、外壁结构应力

3.1.2 按Tresca全屈服准则进行圆筒体的强度计算

(1)保持上述设备参数不变，设计压力为Pc=68.8 MPa时：

根据式(2)可以计算出圆筒体的厚度为：

(2)保持上述设备参数不变，设计压力为Pc=90 MPa时：

同样根据式(2)可以计算出圆筒体的厚度为：

3.2 算例计算结果分析

两个算例计算结果汇总见表3。

(1)利用拉美公式计算的圆筒体内、外壁的应力与有限元分析得出的径向应力、环向应力和轴向应力非常吻合，说明利用拉美公式计算的厚壁圆筒的应力值可以很好地反映应力的分布规律。

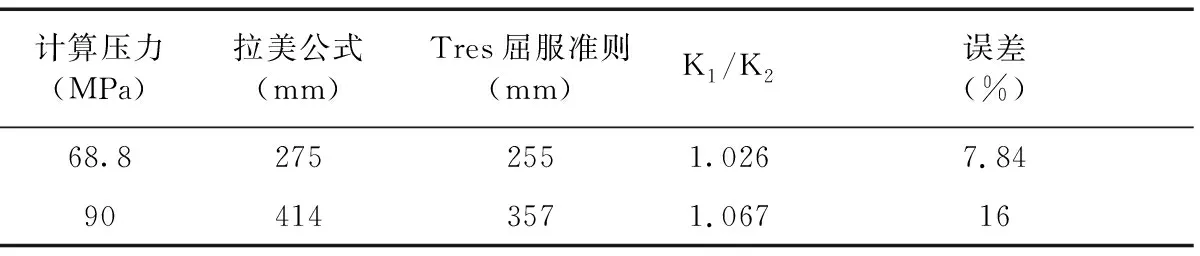
表3 两个算例计算结果汇总

(2) 利用Tresca屈服准则计算的圆筒体厚度比按照拉美公式的弹性失效准则计算的厚度明显地减薄，而且随着K值的增加，两者的误差会进一步地增大。

(3)利用拉美公式计算厚壁圆筒的理论基础是根据第一强度理论推导出，认为筒体中只要最大主应力超过材料的许用应力，该结构就会失效。对于理想的弹塑性材料，此理论计算的结果未能充分发挥材料的承载能力，略显保守。

3.3 厚壁圆筒体开孔补强计算算例

3.3.1 按等面积补强法进行计算

根据JB4732-1995第10章的规定，可以计算出当圆筒体厚度为255 mm时，满足开孔补强所需要的接管最小厚度为t=110 mm。(计算过程从略)

3.3.2 按应力分类法进行计算

应力分析采用ANSYS软件，结构采用SOLID185实体单元，网格采用6面体，在接管与壳体的相贯处对网格进行细化处理，得到的网格模型见图3。

图3 网格划分图

位移边界条件：① 筒体的一端所有的节点施加位移约束：② 限制轴向位移为0；③ 绕轴向轴线的转动自由度设置为0。位移边界约束条件见图4。

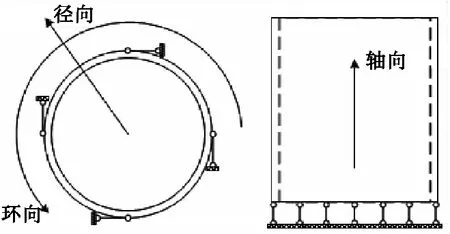
图4 位移边界约束条件

载荷边界条件：

① 圆筒体的另一端施加等效面力：

② 接管的端部施加等效面力：

③ 筒体、接管的内表面施加计算内压Pc；

④ 管口端部施加外部等效面力Pt。

模型经分析后，计算的结构应力云图见图5。

图5 应力强度云图(单位：MPa)

将通过应力分析得到的名义应力，分别在接管根部且垂直于壳体(图6)、接管壁厚的截面(图7)，过结构最大应力强度点的沿表面法线方向(图8)各取一条路径，进行线性化处理。线性化处理后的结果见表4。

图6 应力线性化路径一

图7 应力线性化路径二

图8 应力线性化路径三

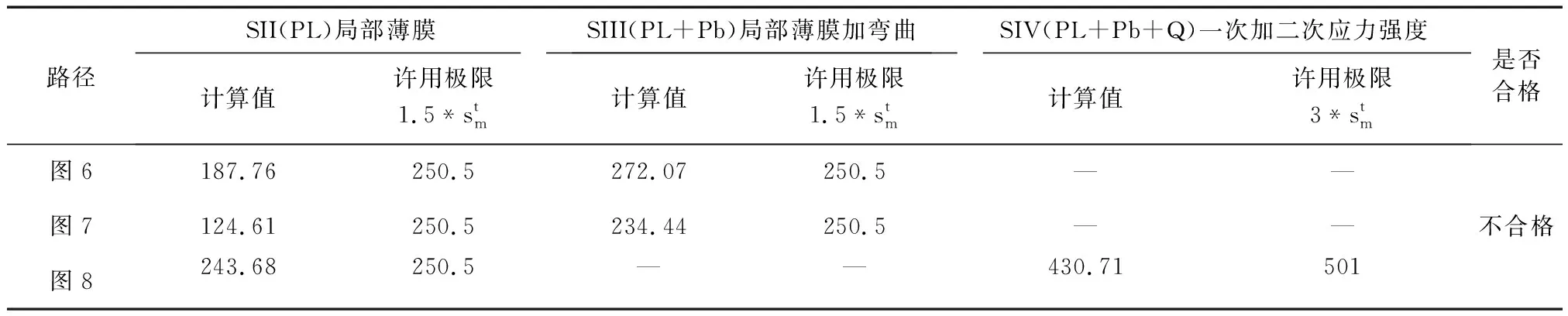
表4 算例3应力线性化结果(MPa)

3.3.3 按极限载荷法进行计算

求结构的极限载荷时，需要按比例增大设计载荷，使结构在TIME<1时不再收敛，以施加的载荷乘以TIME值即可求出结构的极限载荷。根据JB4732-1995的规定，将此极限载荷乘以2/3，即可求出此结构的许用极限载荷。采用此方法求取结构的极限载荷时，认为材料都是理想弹塑性材料，忽略材料进入屈服状态后的应变强化。

根据上述方法，可以求出此结构的载荷—位移曲线，见图9。

根据图9可以得出此结构的极限载荷为114.7 MPa，将此载荷乘以2/3，即：114.7X2/3=76.5 MPa，此载荷即为此结构的许用极限载荷。

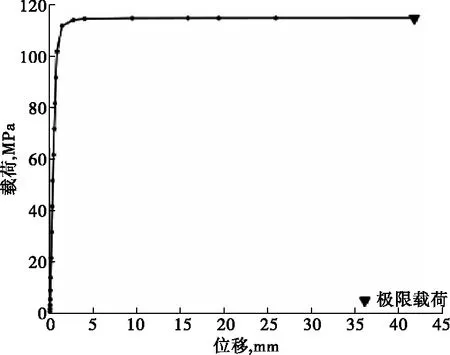
图9 载荷—位移曲线1

3.3.4 按等面积补强法进行计算

根据JB4732-1995第10章的规定，可以计算出当圆筒体厚度为357 mm时，满足开孔补强所需要的接管最小厚度为t=135 mm。(计算过程从略)

3.3.5 按应力分类法进行计算

根据3.3.2的计算方法，可以求出此结构的应力线性化处理结果，见表5。

表5 算例4应力线性化结果(MPa)

3.3.6 按极限载荷法进行计算

根据3.3.3的计算方法，可以求出此结构的应力线性化处理结果，见图10。

根据图10可以得出此结构的极限载荷为151 MPa，将此载荷乘以2/3，即：151×2/3=100.7 MPa，此载荷即为此结构的许用极限载荷。

3.4 算例计算结果分析

(1)通过算例3和算例4可以看出，在圆柱壳开孔同样的条件下，等面积补强法和极限载荷法计算的结果都为合格，而应力分类法计算的结果为不合格。

(2)对于圆柱壳上开孔的结构，JB4732-1995将SII和SIII以1.5倍的设计应力强度作为许用值略显保守，建议可以和GB/T150-2011保持一致，以2.2倍的设计应力强度作为许用值。

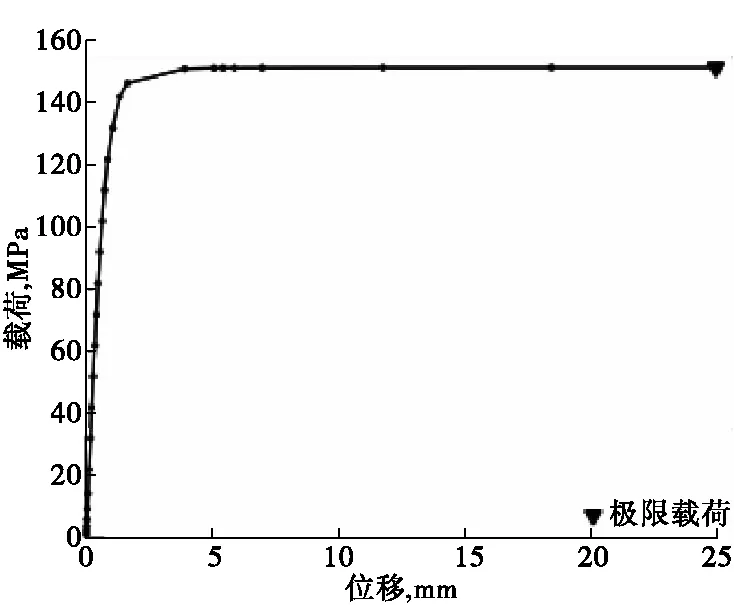
图10 载荷—位移曲线2

(3)采用极限载荷法可能会得出和实际情况比较吻合的结果，但是在分析时，一定要充分考虑接管的各种载荷，否则可能会得到比较冒进的结果。

4 结语

(1)通过以上的分析与计算可以得出，当K>1.5时，由于拉美公式是基于弹性失效准则，所以计算出的厚度会略显保守。而且随着K值的增加，误差会更大。建议厚壁圆筒统一采用Tresca全屈服准则进行设计，可以在保证安全的前提下减少投资，控制成本。

(2)等面积补强法是以补偿开孔局部截面的拉伸强度作为补强准则的，只涉及静力强度问题。对于开孔边缘的二次应力安定性问题是通过限制开孔直径、开孔形状和开孔范围等间接加以考虑的。所以我国的GB/T150.3-2011和JB4732-1995标准都对等面积补强法的使用范围有严格的规定。同时采用等面积补强法时由于无法考虑接管的外载荷，建议在工程设计时采用其他方法确认。

(3)采用应力分类法时，在内压力作用下，接管中存在的轴向应力的合力将作用在筒体与筒体连接处，在该处将为平衡接管轴向力而产生弯曲应力和膜应力，该部分弯曲应力应是一次弯曲应力。然而，在接管与筒体连接处，压力作用下接管和筒体的变形协调也会产生弯曲用力和膜应力，按应力分类原则，该部分弯曲应力应是二次应力，所以，应力线性化处理后所得到的的弯曲应力既有一次应力的成分，也有二次应力的成分。但是，由于应力线性化时无法区分一次和二次弯曲应力，而将弯曲应力全部归属于一次应力，会导致对一次应力的评定偏保守。

(4)采用极限载荷法分析时，ASME VIII-2中规定理想弹塑性材料(不考虑材料的应变强化效应)模型中的屈服限取1.5S，S为材料在设计温度下的应力强度。计算过程中使用Mises屈服条件。同时，JB4732-1995中规定结构的极限载荷乘以2/3，才能作为许用内压使用，因此，以极限载荷法求出的许用压力的安全性是可以得到保证的。

符号说明

Di—筒体内径，mm

D0—筒体外径，mm

K—直径比

dop—接管开孔直径，mm

di—接管内径，mm

d0—接管外径，mm

Pc—计算压力，MPa

Pe—内压圆筒能承受的压力，MPa

Ф—焊接接头系数

δe—圆筒体计算厚度，mm

[σ]t—设计温度下材料的许用应力，MPa

σe—等效应力，MPa