基于粗糙集的社交文本特征选择方法
2021-01-08曹守富蒋慧平
曹守富,蒋慧平,谭 阳
(1.湖南广播电视大学教育信息技术中心,长沙 410004;2.湖南网络工程职业学院网络技术学院,长沙 410004)
一、引言
在社交文本的分类过程中,很多特征项对分类没有意义,它们的存在一方面影响分类的速度,另一方面影响分类的效果。因此,在分类之前需要进行特征选择。常用的特征选择方法有词频(TF)、文档频数(DF)、信息增益(IG)、互信息(MI)和卡方统计量(CHI)[1]等。已有研究表明,卡方统计量和信息增益是文本分类中效率较高的两个特征选择算法[2]。在此基础上,学者们围绕如何提高分类性能进行探讨:一是对期望交叉熵、互信息和信息增益三种特征选择方法进行比较,并提出了进一步改进的方法,经实验验证,改进的期望交叉熵能提高分类性能[3];二是提出了基于互信息和粗糙集的融合特征选择算法[4];三是在信息增益方法中添加合适的比例因子,对信息增益进行改进,使其适应样本均匀和非均匀训练集[5];四是考虑到社交文本内容比较短,特征项较少,为了扩展社交文本的特征,提出了一种微博特征提取方法[6];五是提出了一种基于粗糙集与概率加权的特征选择算法,通过计算依赖度结合特征项在微博中出现的概率来实现特征选取[7];六是提出了基于WordNet语义特征选择方法,通过WordNet减少和消除特征项的歧义[8];七是提出利用粗糙集理论并采用约翰逊启发式属性约简的方法来达到特征选择的目的[9]。
上述的改进方法各有优点,在一定程度上解决了分类过程中特征选择的问题,但不足之处是无法自动确定特征项的选择数目,即选择的特征项数目不能够支持算法正确区分文本集中各条文本所属分类。本研究在分析特征选择常用方法的基础上,提出一种基于粗糙集的社交文本特征选择方法(RS):利用方差衡量特征项的类间波动情况,波动越大表明其类别区分度越高,以此作为先验知识对已有的决策表进行约简,获取的属性集即核心选择特征项;使用核心选择特征项可区分文本集中的文本,在此基础上若适当补充其他属性,可达到更佳的特征选择效果。
二、粗糙集理论

决策系统DS也称为决策表,表示为DS=(U,A=C∪D,V,f)。DS将信息系统的属性集A划分为两个集合,即条件属性集C和决策属性集D,即A=C∪D,C∩D≠∅,D≠∅。那么在决策系统DS=(U,C,D,V,f)中,对于U中任意两个对象ui和uj,若在条件属性子集P(P⊆C)上的取值相等,即∀a∈P,a(ui)=a(uj)成立,则称对象ui、uj对于属性集P是不可区分的,表示为:
IND(P)={(ui,uj)|(ui,uj)∈U×U,∀a∈P,
a(ui)=a(uj)}
(1)
在决策信息系统DS=(U,C,D,V,f)中,对于∀P⊆C∪D,若U/P={P1,P2,…,Pm}且X⊆U,则称P-(X)=∪{Pi|Pj∈U/P,Pi⊆X}为X关于属性集P的下近似集,称P-(X)=∪{Pi|Pj∈U/P,Pi∩X⊆≠∅}为X关于属性集P的上近似集。在DS中若U/D={D1,D2,…,Dk}为决策属性D对U划分形成的决策类,对于P⊆C,若U/P={P1,P2,…,Pm}为条件属性P对U划分形成的条件类,则POSp(D)称为条件属性集P关于决策属性集D的正区域。
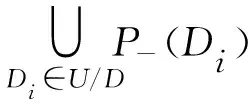
(2)
若在决策信息系统DS=(U,C,D,V,f)上存在两个等价关系族C和D(C,D⊆DS),对于∀P∈C而言,如果P是C相对于D的独立子集,并且POSp(D)=POSC(D)成立,则称P为条件属性集C相对于决策属性集D的正区域模型下的知识约简[10]。
三、构建决策表
(一)计算属性权重
社交文本的特性为文本长度较短,但总体的词汇量较大,在不同的时间段会派生出许多新的词汇,训练集中出现的词汇一般遵循Zipf定律,即只有少数词汇被经常使用[11]。大量词汇在训练集中出现的次数很少甚至只出现1次,这些词汇被称为稀有词汇,它们对分类的特征选择贡献度很低。因此,在构建决策表时,可以把每个特征项作为决策表中的一个属性看待,计算得出的属性权重即特征项权重。本研究在计算权重时,过滤了出现次数少于或等于3次的词汇,过滤后再根据训练集D={d1,d2,…,dn}得到所有社交文本的特征项集合T={t1,t2,…,tm},以每条文本在相应特征项的取值计算该特征项的权重,计算权重采用TF- IDF权重计算方法。表1给出了两条社交文本中部分特征项的权重值,可以看出:“Mobile”类别中编号为“1141”的社交文本包含了“魅族”“诺基亚”这两种类别区分度较高的特征项,其权重值相对较大;而特征项“微博”“转发”这两种类别区分度较低的特征项,其权重值相对较小。
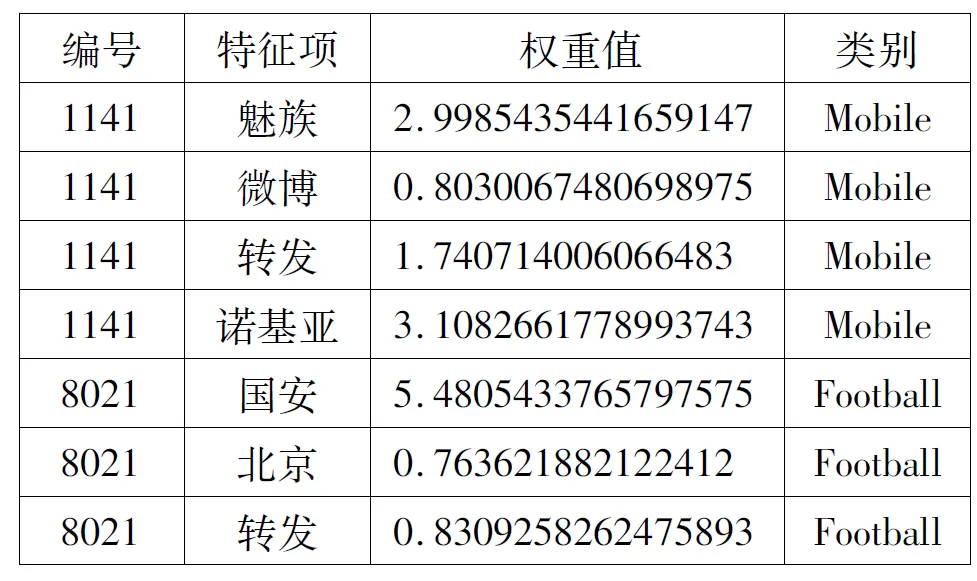
表1 部分特征项权重比较
(二)对属性值作离散化处理
在向量空间模型中计算得到的每个属性权重值是连续的,约简之前需要进行离散化处理。本研究采用等距离划分的数据离散化方法,每个特征项的权重值按等距离划分为2个区。表2显示了对关于“手机”“篮球赛”的部分特征项权重作离散化处理的结果。
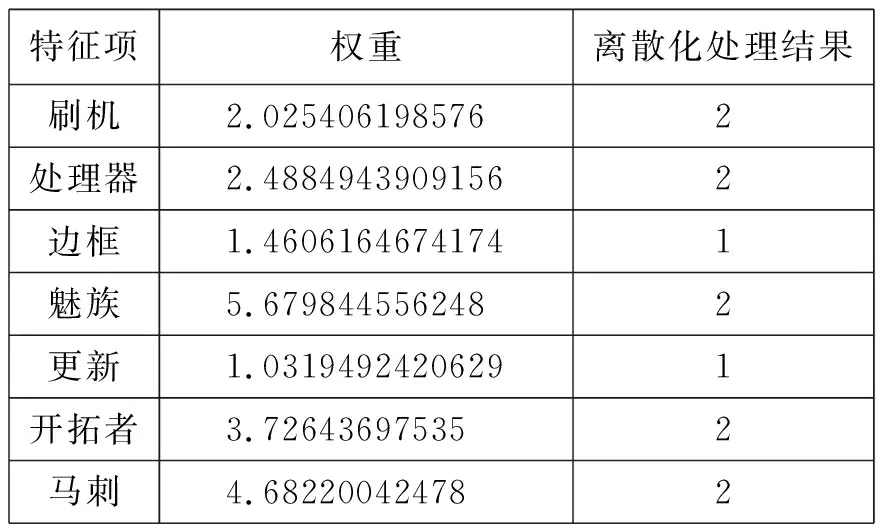
表2 部分特征项权重的离散化处理结果
(三)生成决策表
训练集中的每个对象要表示成粗糙集能够处理的决策表形式,在此使用向量空间模型来表示社交文本信息。将整个训练集作为论域,以训练集中的每一条文本为论域中的对象,每个对象包含的特征项为条件属性,经过离散化处理的特征项权重值为条件属性值,其所属类别为决策属性,以此构建决策表。如果某些特征项在一条社交文本中没有出现,则将其对应的属性值设置为0。构建的决策表形式如表3,其中特征项是条件属性,类别是决策属性。
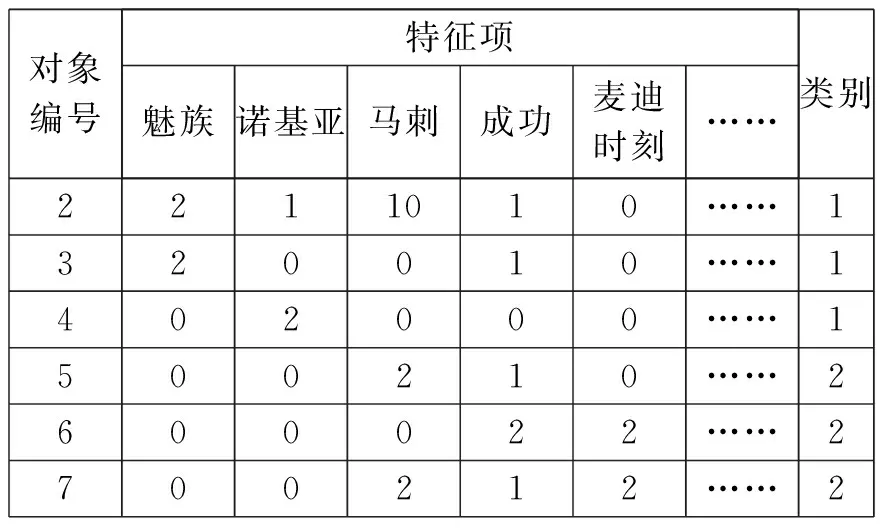
表3 离散化处理后的决策表
四、属性排序及约简
(一)条件属性排序及归类
在对决策表进行属性约简时,要不断向条件属性子集按照特定顺序加入新的属性,然后判断新的条件属性子集是否为一个约简。这就需要对属性进行排序,然后将每个属性划分到相关的一个或多个类别中。本研究用方差衡量属性(特征项)在各类别之间的波动,波动越大,则该类别的区分度越高。具体算法如下:
输入:未离散化的决策表DS=(U,C,D,V,f)。
输出:已排序和归类的属性类别关系矩阵。
第一步:在未作离散化处理的决策表中,按类别分组,计算每个分组中每一列的和,即某个属性在该类别中的权重值之和,这样每个类别最终都会对应一个向量v=(∑Wi1,∑Wi2,…,∑Wij,…,∑Win),其中∑Wij为类别i中属性j的权重值之和。
第二步:将上一步每个类别对应的向量v组成一个矩阵M,m个类别n个属性对应的矩阵为M。
(3)
第三步:计算矩阵M每一列的方差,将它们组合成一个向量q=(σ1,σ2,…,σn),q中分量σj反映了属性j在类间分布的波动情况。
第四步:将q中的分量值从大到小进行排序,形成一个新的向量q′,同时调整属性的排列顺序,矩阵M中的各列也根据q中分量的排序情况进行调整,形成新的矩阵M′。
第五步:将各属性划分到各个类别中。对属性j划分的方法为:计算M′中第j列的最大值max∑Wij,其中1≤i≤m,最大值对应的类别即为该属性对应的类别;然后计算∑Wkj/max∑Wij,其中1≤k,i≤m,k≠i,,即该列的其他分量与最大值的比值;设置一个阈值β,当∑Wkj/max∑Wij≥β时,将该属性划分到max∑Wij对应的类别。
第六步:输出已排序和归类的属性类别关系矩阵P。
(4)
每一行是划分到某一类的属性,值得注意的是,各类别所包含的属性数量可能不同,并且一个属性可能同时属于多个类别。在选择属性时,按列的方向从上到下、从左到右依次选择,当遇到已选择的属性时跳过当前属性,选择下一个,详情见图1。采用这种选择策略是为了保证各个类别所包含的特征项数量均等,避免和减少因特征项不平衡而导致分类器有所偏好。
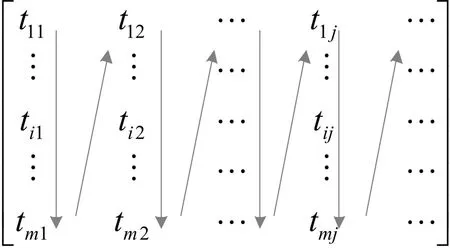
图1 特征选择顺序
(二)属性约简
决策表属性约简一般采用启发式的约简方法得到一个最优或次优的约简,如基于属性重要度的属性约简算法[12],或基于区分矩阵的属性约简算法[13],这些方法需要计算核属性。由于本研究根据社交文本信息生成的决策表属性数目多且属性值分布稀疏,采用核属性计算方法得到的结果经常是空集。因此,在初始属性选择方法上采用前文所述方法,按顺序选取少量属性作为约简的初始条件属性集,记为S,以排序后的向量q′中的分量值作为启发信息来实现约简。属性约简的具体算法如下:
输入:决策表DS=(U,C,D,V,f)。
输出:条件属性集C相对S的一个约简及新的属性类别关系矩阵P′。
第一步:从属性类别关系矩阵P中选择m个条件属性组成初始条件属性集S,记录初始条件属性集最后一个属性在P中的位置Pos,令R=S,Posend是P中最后一个元素的位置。
第二步:若POSR(D)=POSC(D),则转到第七步,否则令T=S。
第三步:设置Pos=Pos+1。
第四步:在矩阵P中从Pos至Posend,按属性选择顺序依次选取属性c,如果c在T中存在,则跳过当前属性选择下一个,否则将c加入到T中,直到POST(D)=POSC(D),记录c此时所在的位置Posc,并设置Posend=Posc。
第五步:设置R=R∪{C},T=R,调整c在矩阵P中的位置,将其插入到Pos位置处,该位置对应行的后面元素依次向后移动。
第六步:如果Posend=Pos,表明找到了一个包含属性较少的约简结果,此时属性类别关系矩阵已经发生变化,新的属性类别关系矩阵记为P′,转到第七步。若Posend≠Pos,则转到第三步。
第七步:输出约简结果R及属性类别关系矩阵P′,算法结束。
R中包含的属性是能够区分训练集中所有样本的一个较小属性集,我们在选择特征时应该包含这些特征项。在特征选择时,选择的特征项数目应该大于或等于|R|,即大于或等于约简后的属性数,这样就保证了选择的特征中包含正确分类的特征项。
五、实验分析
为了能够明确RS方法的性能,本研究选取词频数(TF)方法、文档频数(DF)方法、互信息(MI)方法及卡方统计量(CHI)方法进行比较。实验在同一环境下进行,对5种方法用Java语言进行重写,分类方法采用朴素贝叶斯分类方法。实验数据集来源于新浪微博中63641个用户的真实数据集[14]。为了有效提取文本特征,避免数据过于分散,我们从63641个用户中分类提取了5类数据,分别为:手机类、足球赛类、篮球赛类、电视剧类和房地产类。通过基本的数据清理,一共筛选出长度在14个字符以上的有效数据6000条,并由人工分别对其进行类别标注。其中,均匀训练集中每个类别700个数据,共3500个训练样本;非均匀训练集中各类样本数量分别为900、600、1200、300、600,共3600个训练样本。实验环境为:Core i5 3.3GHz的CPU和8GB的RAM。
比较采用查全率r、准确率p、F1值作为性能评价指标。准确率(查准率)是针对预测结果而言的,表示当预测为正的样本中真正的正样所占的比率。查全率(召回率)是针对原来的样本而言的,表示样本中的正例被预测正确的比率。F1值为综合评价指标,F1=2pr/(p+r)。另外,属性归类时需要确定阈值β,本研究针对β的不同取值对算法性能的影响进行了对比实验。实验结果表明,当取值为0.65时分类算法取得了较好的性能,因此在后续的实验过程将β设置为0.65,详见图2。
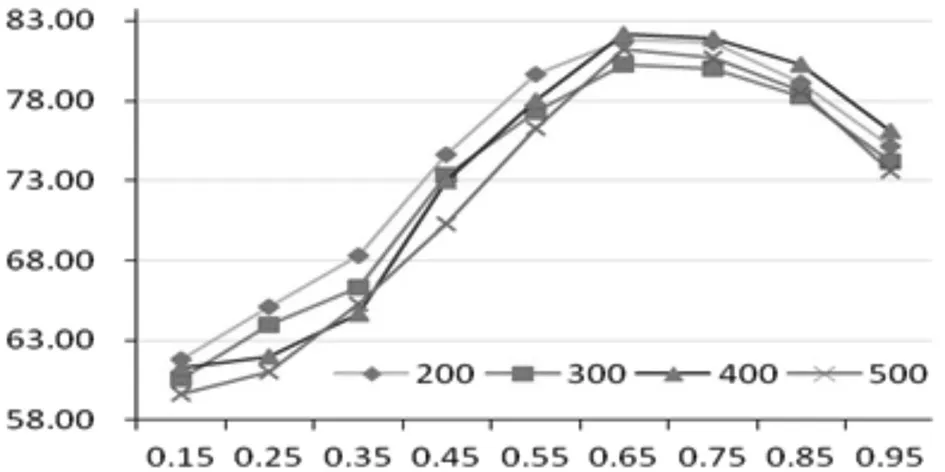
图2 不同阈值对分类性能的影响
(一)属性约简后的特征项分类性能对比
经过清除稀有词汇,均匀训练集中有3353个特征项,通过属性约简取130个特征项。对于5种方法分别独立运行20次,得到其在均匀数据集上特征选择的平均值。表4中列出了5种方法在均匀训练集上的特征选择情况,通过属性约简大幅降低了数据向量空间的维度。可以看出,RS方法在查全率和准确率上均优于其他方法,表现出更好的文本分类性能。
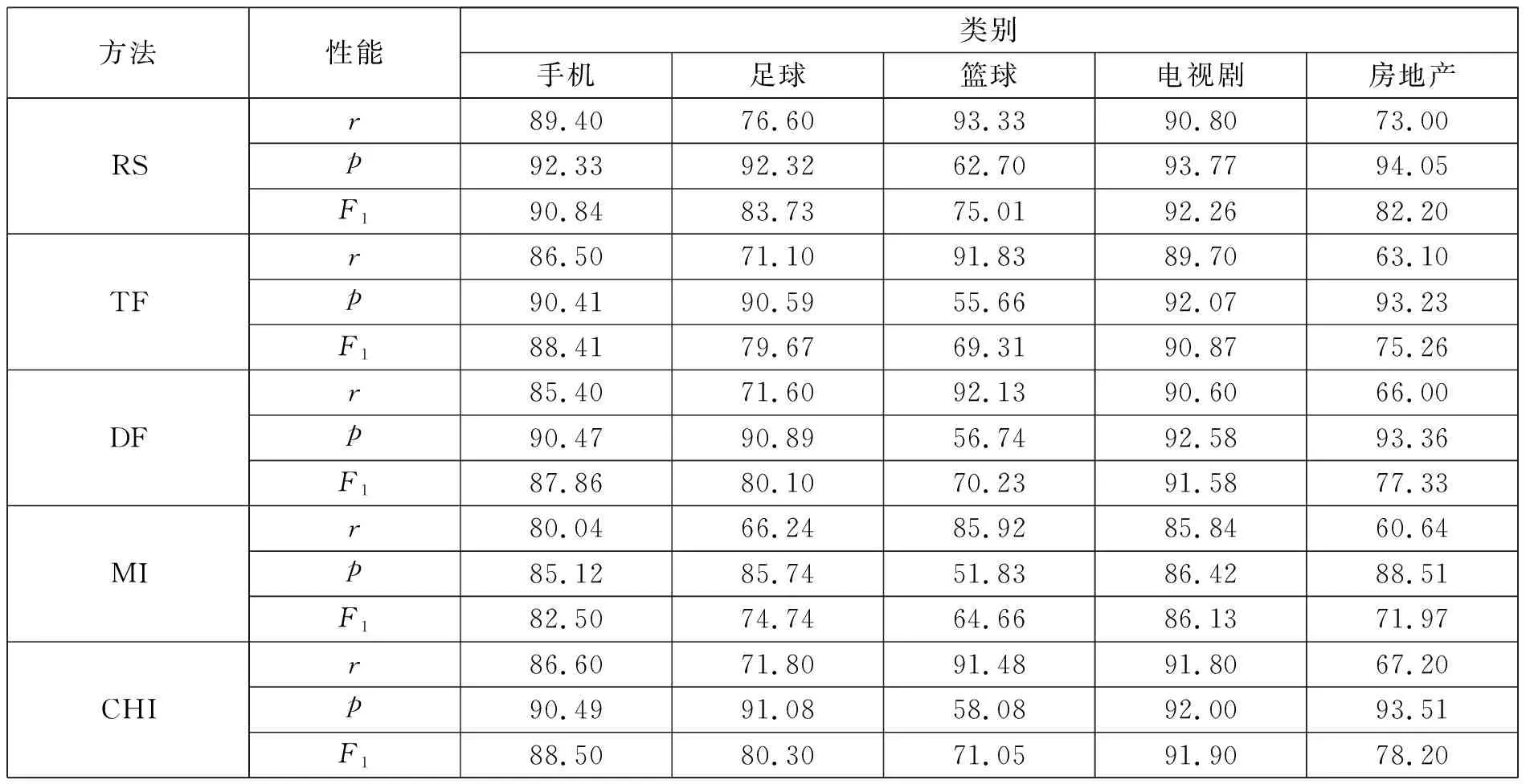
表4 5种特征选择方法在均匀训练集上的性能比较
为了进一步验证RS方法的性能,还可以采用非均匀训练集进行对比测试。非均匀训练集中共有3890个特征项,经过清理和约简,保留了112个特征项。表5中列出了5种方法在非均匀训练集上的特征选择情况。
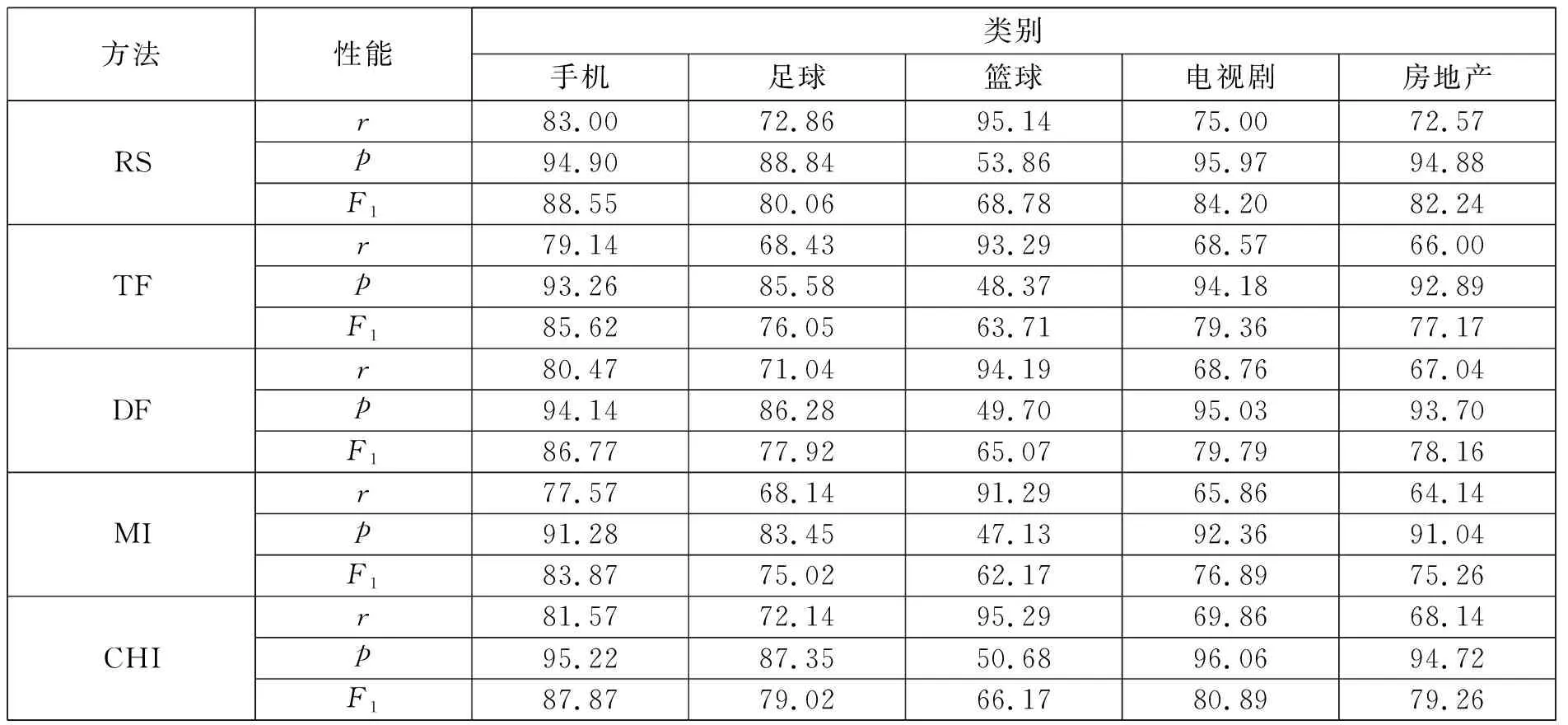
表5 5种特征选择方法在非均匀训练集上的性能比较
从表4和表5可以看出,跟其他4种方法相比,RS方法具有比较优势。在样本均匀情况下的分类性能普遍高于非均匀情况下的分类性能,其原因在于在样本非均匀情况下选择相同数量的特征项,由于样本数的差距,每个类别的特征项分类能力会有所差异。
(二)特征项数量不同时的分类性能对比
用实验验证在不同数量特征项情况下5种特征选择方法的分类性能,图3是在样本均匀情况下不同方法的分类性能(F1值)对比。可以看出,当特征项数量在400~500范围内时,所有特征选择算法均达到了自身性能的最佳状态,但RS方法的分类性能均优于其他对比方法,虽然在特征项数量大于700后性能有所下降,但仍然优于其他对比方法,表现出更好的鲁棒性。
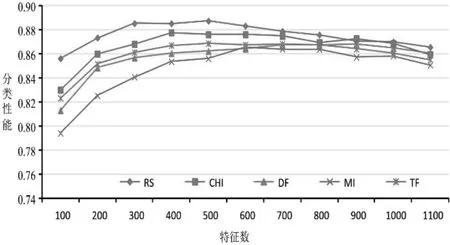
图3 样本均匀情况下的分类性能
图4是样本非均匀情况下分类性能(F1值)的对比情况。可以看出,RS方法在特征项较少(小于800)时分类性能高于其他方法,这是因为该方法选择的特征项至少能够保证正确地对训练样本集进行分类,而其他方法不能保证。当特征项数量达到一定规模(1200~1600)后,分类性能最佳,如果继续增加特征项数量,分类性能反而下降,这是因为过多的特征项中会包含无意义的、有噪声的特征项。
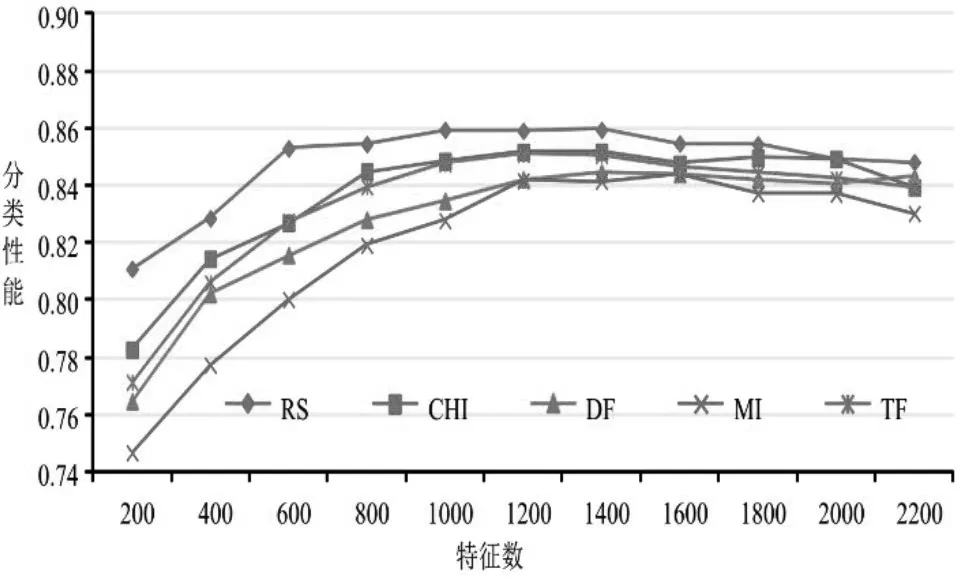
图4 样本非均匀情况下的分类性能
六、结语
本研究利用方差衡量特征项的类间波动情况,波动越大表明其类别区分度越高。将特征项按方差大小进行排序,然后将其均匀地分配到各个类别中,形成一个特征项类别关系矩阵P。对属性进行约简时,需要选择初始属性,从P矩阵中按照指定顺序选取少量属性作为初始属性,然后按属性的波动大小作为启发信息,不断加入新属性寻找一个约简结果,直到初始属性集稳定。实验结果表明,该方法可以大幅度减少特征项数量并能保持较好的分类效果。当特征项数量在约简结果的基础上适当增大时,本方法的分类性能同样优于常用的4种特征选择方法。
