分时段交通流荷载效应分析

2021-01-08张明孔艳冬刘扬鲁乃唯殷新锋颜巍

铁道科学与工程学报 2020年12期

张明，孔艳冬，刘扬，鲁乃唯，殷新锋，颜巍, 3

分时段交通流荷载效应分析

张明1，孔艳冬2，刘扬1，鲁乃唯1，殷新锋1，颜巍1, 3

(1. 长沙理工大学土木工程学院，湖南长沙 410114；2. 绍兴市交通工程质量安全监督站，浙江绍兴 312000；3. 中国公路工程咨询集团有限公司，湖北武汉 430040)

为研究不同时段车辆运营状态对荷载效应的影响，基于南溪长江大桥100多万车辆的动态称重(WIM)实测数据，统计白天和夜间2个时段车辆荷载参数，建立分时段的随机车流荷载模型；研究三跨连续梁桥的分时段车流荷载效应，将设计基准期内的外推极值与设计规范对比分析。研究结果表明：受到重车/超载车辆的影响，行车道白天与夜间的车重均服从混合高斯分布，而超车道的白天与夜间车重均服从对数正态分布；白天夜间车头间距均服从对数正态分布；随机车流作用下的桥梁荷载效应服从对数正态分布，用于极值外推的最大荷载效应服从极值I型分布；随机车流与实测车流作用下荷载效应外推极值相对误差在10%以内；根据不同时长编制的随机车流作用下的荷载效应外推值大于规范值。

公路桥梁；车辆荷载模型；活荷载效应；极值外推；随机过程

随着城市道路的高速发展，交通量日益增长，如何准确又高效的评估车辆荷载对桥梁产生的荷载效应成为热点问题。我国《公路桥涵设计通用规范》(JTG D60—2015)[1]对汽车荷载的计算图式、荷载等级及其标准值等均做出具体规定，有一定的参考价值。但车辆荷载具有时效性和地域性，不同地区的车辆荷载差异大，因此针对某一地区的实测车辆数据编制随机车流才更符合实际车况。此前国内外许多学者对此展开过研究。Nowak等[2]考虑车辆荷载参数和车队过桥的影响线函数卷积计算桥梁的荷载效应。GU等[3]通过贝叶斯极值函数分析车重概率分布。Enright等[4]采用蒙特卡洛方法模拟车流并分析其对桥梁结构效应的影响。宗周红等[5]采用实测数据，对新沂河大桥车辆荷载模型进行研究。韩大章等[6]根据计重收费数据，采用极值外推法对桥梁进行评估。刘浪等[7]利用短时间内的车辆数据计算并外推到基准期内的荷载效应。上述学者基于实测数据针对荷载模型或桥梁的荷载效应进行了一定的研究[8]，但从时段的角度综合考虑车辆荷载参数，计算荷载效应值亟待研究。本文结合南溪长江大桥连续的WIM数据，从不同时间段、不同时间周期对车重、车头间距等车辆荷载参数展开统计分析，建立概率模型。基于蒙特卡洛法应用MATLAB软件编制随机车流，通过有限元软件提取某三跨连续梁桥关键截面处的内力影响线，将随机车流和实测车流加载到影响线上分别求取相应的车辆荷载效应。基于经典极值理论对不同时间周期的弯矩剪力极值展开外推计算，得到不同设计基准期的荷载效应极值分布函数并求取0.95分位值，并与规范公路I级产生的荷载效应对比。

1 项目描述

本文使用的车辆荷载数据来自于G93成泸渝环线高速公路上南溪长江大桥的WIM动态称重系统。WIM动态称重系统主要利用传感器等元件，对通过南溪长江大桥的车辆轮胎状态进行监测，进而采集得到测试车辆的车型、重量、总重、轴重、车速和车距等数据，南溪长江大桥的动态称重系统示意如图1所示。基于WIM系统对宜泸高速南溪长江大桥路段进行为期1年6个月(2014−01−01～2015−06−30)的监测统计。南溪长江大桥位于国家高速公路网G93成泸渝环线高速公路上。该环线从成都经绵阳、遂宁到重庆潼南、铜梁、江津、再经合江、泸州、宜宾、乐山、雅安返回成都，如图2所示。成泸渝环线总里程1 200多km，是目前国内总里程数最长、串接城市最广的环城高速。该地区超载车辆频现，于我国西南而言很有代表性。

图1 WIM系统示意图

2 车辆荷载参数统计

2.1 交通量

为描述车辆荷载的时变性，将时间周期划分为1日、1周、1个月、3个月、半年及一年，且每日划分为白天和夜间2个时段，以早晚7点为界限。以一个月数据为例：全天交通流量白天出现2次高峰，分别在10点和17点，且车流量为745辆和723辆；而晚上以重车为主，凌晨3点重车占比高达45%。

2.2 车重

为区分车道间差异给出车道1(行车道)和车道2(超车道)作为代表。同上节时间周期划分对车重展开统计分析得：1) 无论白天夜间，车道1车重的均值和最大值都远大于车道2，说明重车多分布在车道1；2) 车道1白天车重均值明显小于夜间，车道2白天夜间均值差异不大，说明车道1重车多出现在夜间；3) 白天车重的标准差小于夜间，车道1车重的标准差大于车道2；4) 车道1车重的变异系数白天大于夜间，车道2变异系数白天小于夜间。

图2 成泸渝环线高速公路

为直观描述车重的概率分布，需建立相应的概率模型。以一年的车辆荷载数据为例，由于车重数据较集中，因此车道1和车道2的车重取对数后呈多峰、单峰特征，故分别用混合高斯模型、对数正态分布描述。对于混合高斯模型引入赤池(AIC)和贝叶斯(BIC)2种信息判别准则[9−10]权衡实测数据间的拟合程度。以一年白天车道1的车重数据为例，如图3可知当高斯分量数为3时，高斯混合模型与实测数据拟合最优。

基于车道1和2的车重数据，绘制累积概率密度图并与规范对比，如图4(a)可知：1) 车重小于2.6 t时，实测数据中白天夜间小型车占比与规范基本相同；2) 车重在2.6～20 t之间时，实测数据中白天夜间轻型车占比小于规范；3) 车重大于20 t时，夜间重车占比超过白天和规范；4) 参照规范规定从概率统计的角度出发，分位值在0.95处时，白天和夜间车重分别为56.4 t和118.4 t，规范的车重为20 t；分位值在0.997处时，白天和夜间车重分别为160 t和170 t，规范的车重为55 t。

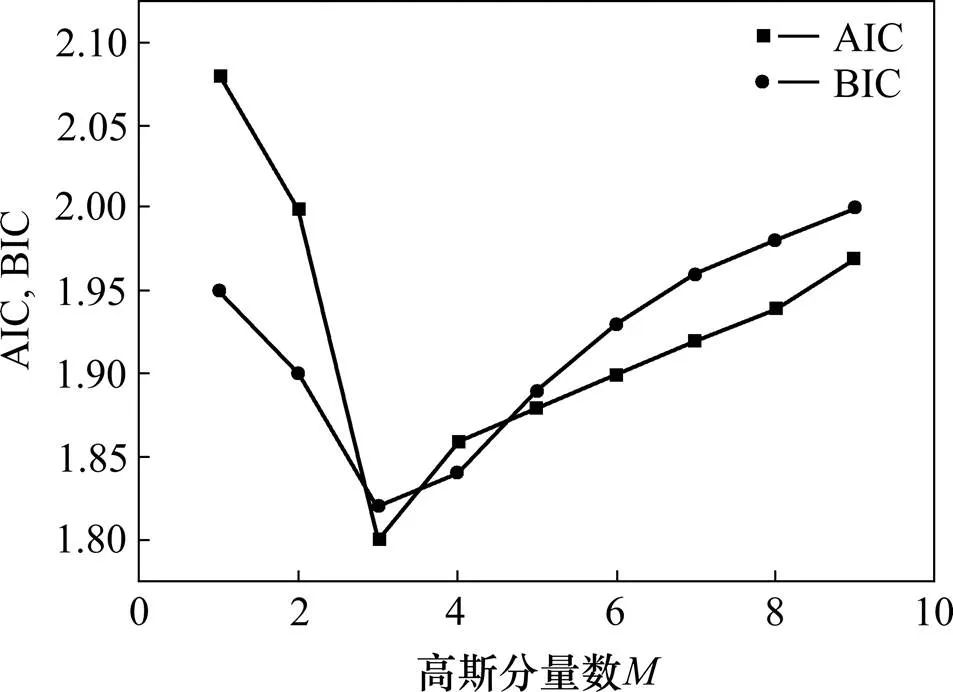
图3 高斯混合模型信息准则值变化曲线

(a) 车道1车重累计概率密度；(b) 车道2车重累计概率密度

如图4(b)可知：1) 白天夜间车车辆占比基本相同；2) 车重小于2.6 t时，实测数据中白天夜间小型车占比小于规范；3) 车重在2.6～10 t之间时，实测数据中白天夜间车重占比大于规范4) 车重大于10 t时，实测数据中白天夜间车重占比小于规范，且实测车重基本集中在10 t以下；5) 参照规范规定从概率统计的角度出发，分位值在0.95处时，白天和夜间车重分别为81.3 t和82 t，规范的车重为20 t；分位值在0.997处时，白天和夜间车重分别为87和92 t，规范的车重为55 t。

基于上述分析，因受到重车/超载车辆的影响，行车道和超车道的车重大于规范规定值。

2.3 车头间距

同上节取车道1和车道2作为代表。对车距在3.1～30 000 m的实测数据进行分时段统计分析。以一年的车辆荷载数据为例，由图5和表1可知：1) 4组样本均服从对数正态分布；2) 车道2车头间距大于车道1；3) 夜间车头间距大于白天，且分布更为离散；4) 白天车道1和2，夜间车道1、2车头间距分别集中在：292.6，370.6，962.3和1136.5 m。

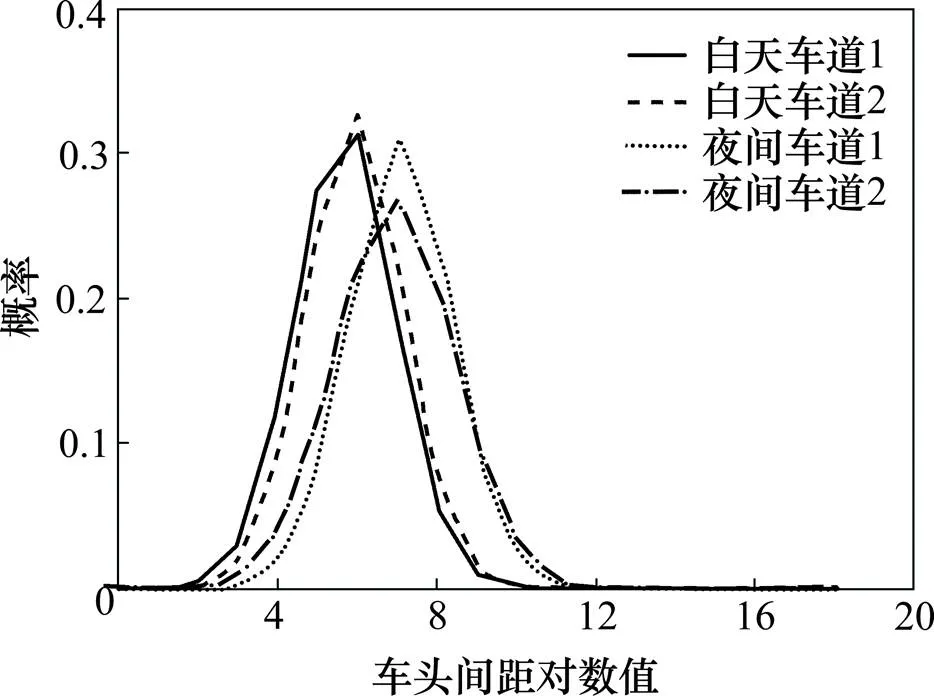
图5 各车道车头间距概率密度

表1 各车道车头间距概率密度模型参数

3 基于蒙特卡洛法的随机车流建模

Monte Carlo法是一种随机化的方法，通过随机采样使统计结果逼近真实值，采样量越大，统计结果越精确[11−13]。根据相关性分析可知车重和车头间距的相关性仅为0.014，视为不相关，在车流模拟时可将2种分布的随机数直接组合。基于蒙特卡洛法编制随机车流如图6所示。

表2 抽样占比及日均样本数

根据不同时间周期内各时段及车道的交通量确定日均样本容量和抽样占比。考虑到样本数的波动和交通年增长率，将日交通样本容量设为8 000。抽样占比及日均样本数如表2所示。

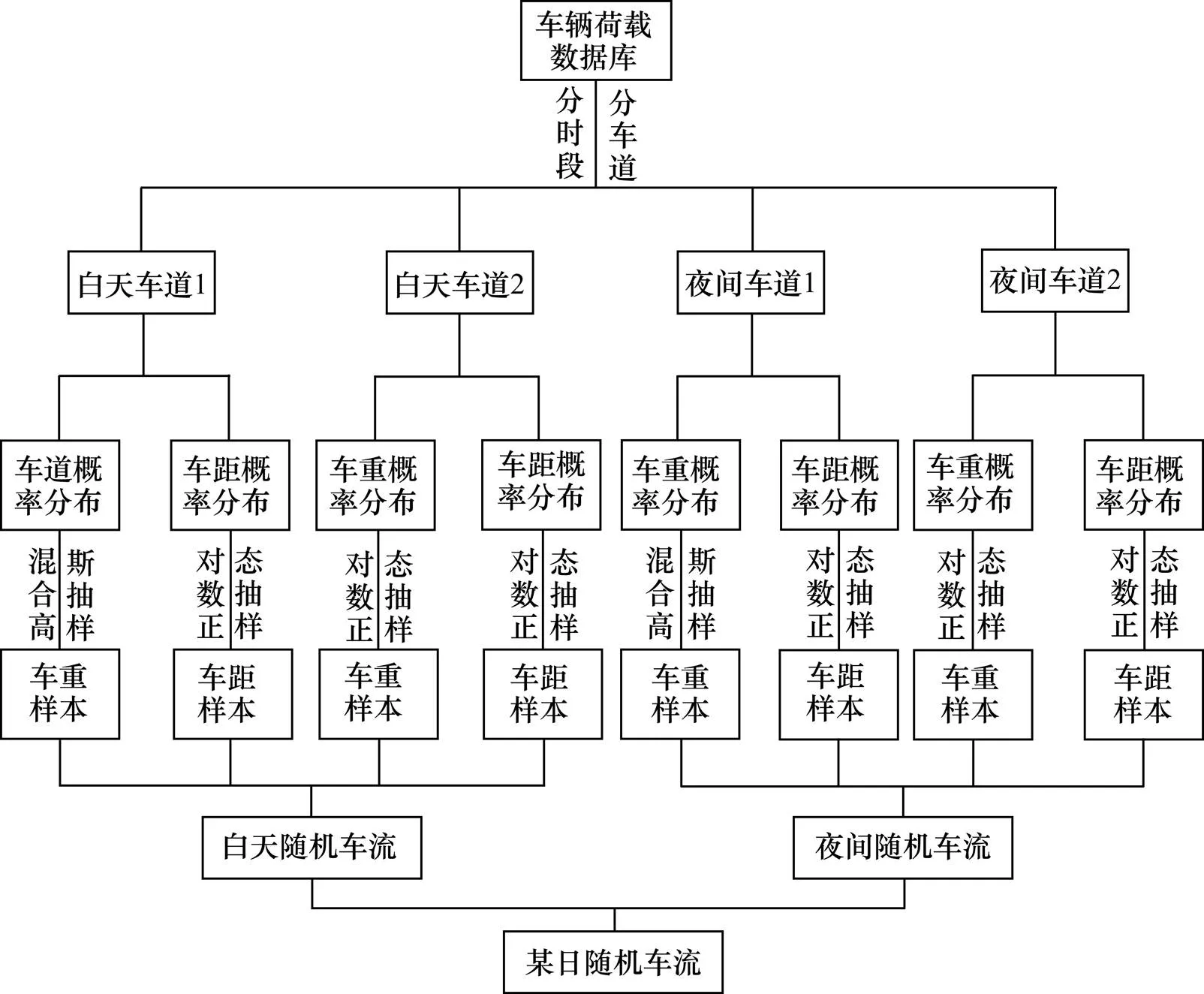
图6 编制随机车流流程图

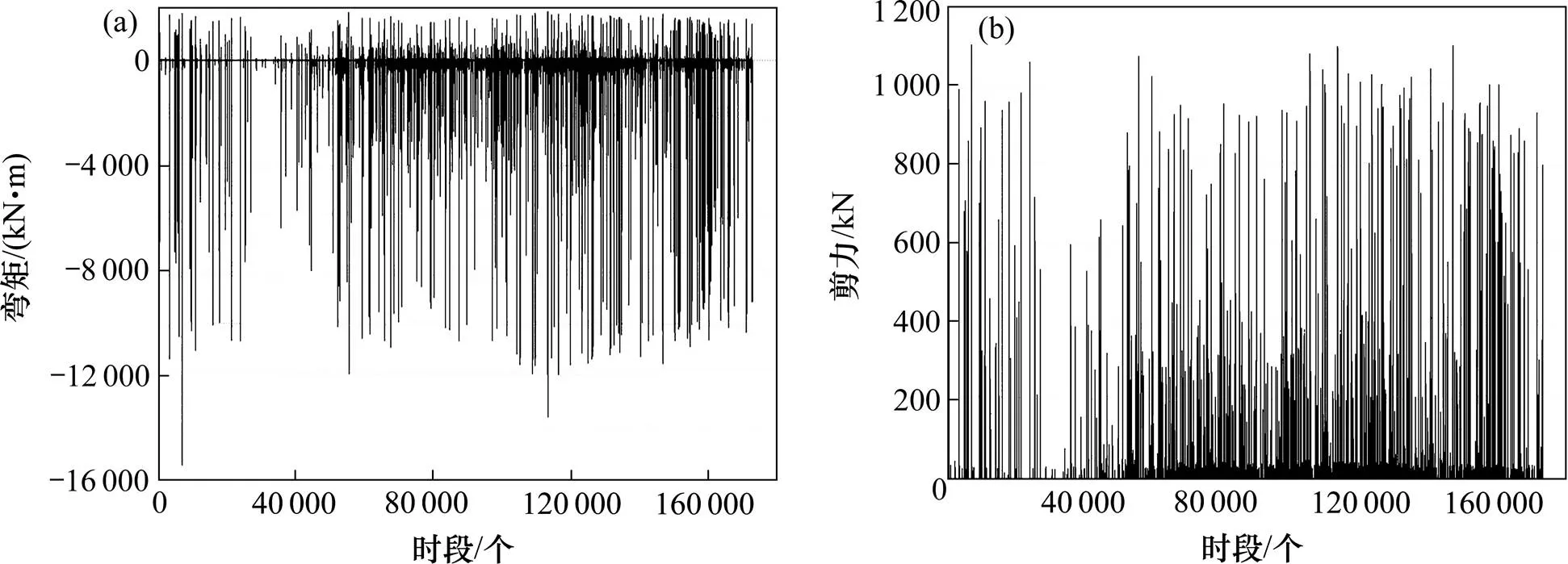
(a) 弯矩时程图；(b) 中支点剪力时程图

4 随机车流下连续梁桥荷载效应分析

4.1 荷载效应计算

为体现随机车队变化的状态，运用马尔科夫链描述车队过桥。根据WIM数据得到车队中每辆车的相对位置、车速、车重等参数；通过影响线加载的方式计算出多车同时作用在桥上时产生的荷载效应；让车队顺次移动，依此计算出整个车队过桥产生的荷载效应[14]。以跨径为48 m+80 m+48 m和车道布置为双向4车道的某三跨连续梁为例展开荷载效应分析。根据日均车流量和抽样比率产生24 h的随机车流，设循环步长为0.5 s，循环周期为1 d，生成荷载效应时程曲线如图7所示。以车道1为例，重复以上步骤，可以得到不同时间周期的随机车流作用下最大荷载效应服从对数正态分布，见表3所示。

4.2 基于经典极值理论的荷载效应外推

根据上节推出最大荷载效应，采用极值统计学的方法展开外推[15−16]，并对各时段的高尾数据进行概率统计。研究发现随机和实测车流作用下最大荷载效应均服从极值I型分布，以随机车流作用下的最大荷载效应为例，其统计参数如表4所示。假设最大荷载效应在各最小时间段内服从独立同分布，由单日、单周等时间周期的分布函数外推不同设计基准期的分布函数并取其0.95分位值作为该设计基准期内的荷载效应极值如图8所示。

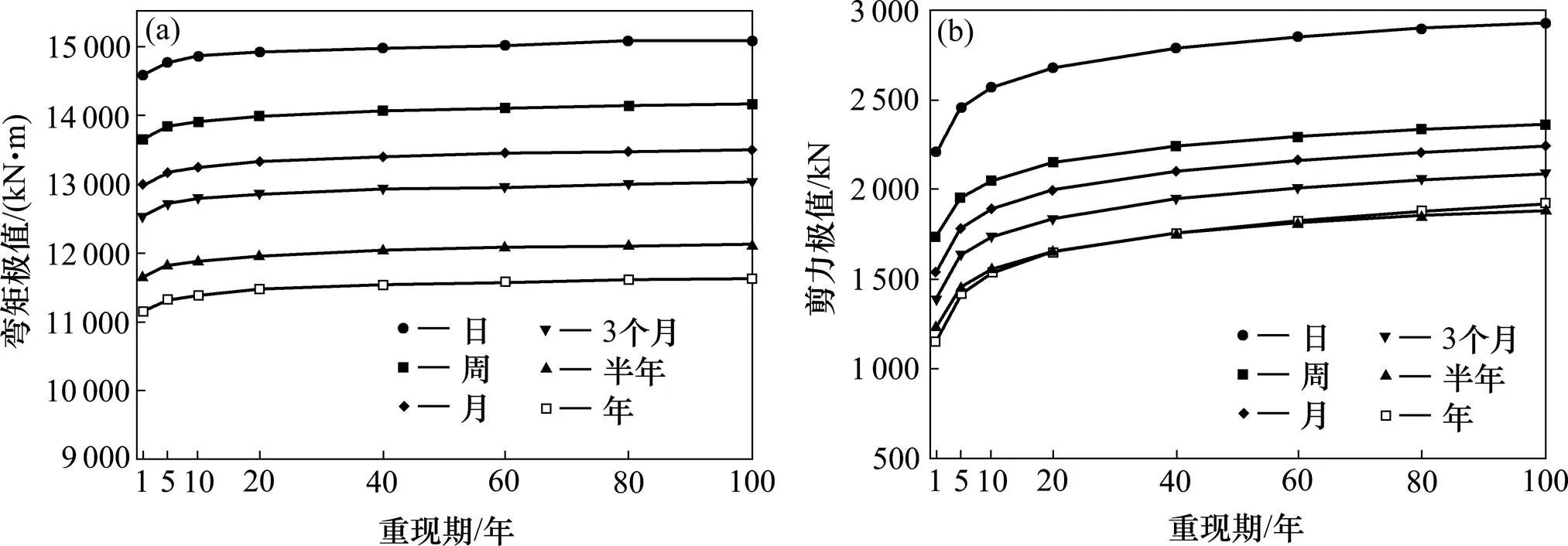
(a) 不同时间周期外推弯矩极值0.95分位值；(b) 不同时间周期外推剪力极值0.95分位值

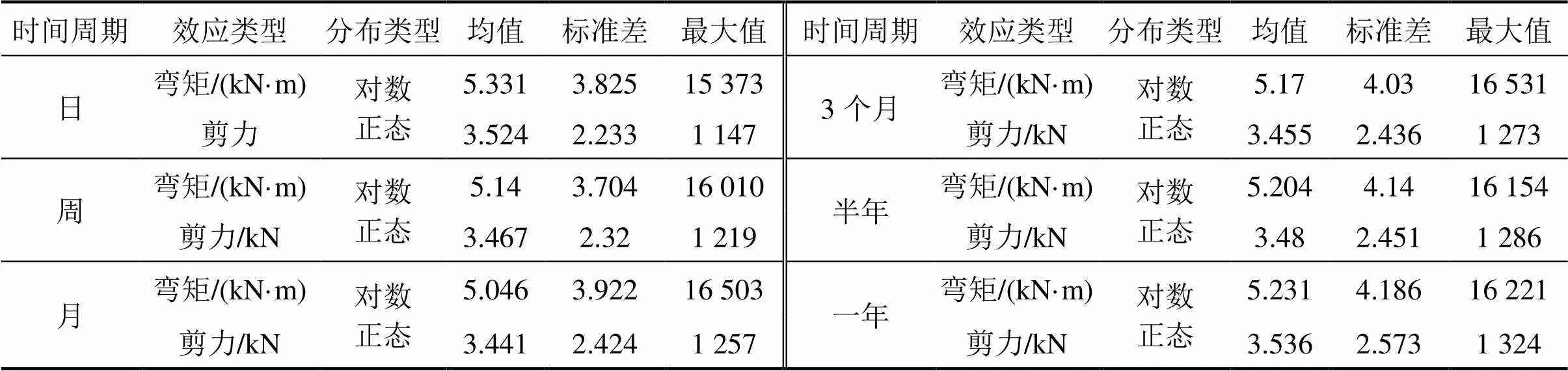
表3 不同时间周期最大荷载效应统计参数

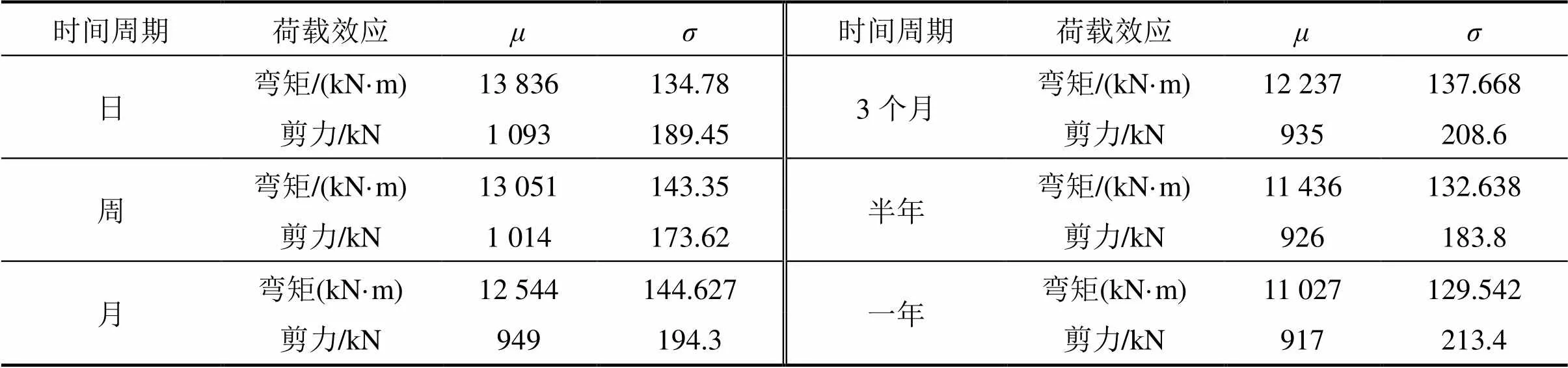
表4 随机车流作用下不同时间周期最大荷载效应统计参数

以实测车流最大荷载效应作为样本时，不同时间周期内最大荷载效应同样服从极值I型分布，使用不同时间周期的极值分布函数外推不同设计基准期的分布函数并取其0.95分位值作为该设计基准期内的荷载效应极值[17]。将随机车流作用下外推荷载效应极值计算结果与实测的随机车流计算结果的比值定义为偏差系数。由图9可知：1) 用时间周期为年的最大荷载效应外推设计基准期为100年时的弯矩偏差系数为0.97，剪力偏差系数为0.92；2) 以日、周、月为时间周期时，偏差系数波动较大，而以3个月、半年和年为时间周期时，偏差系数逐渐趋于稳定, 稳定后的相对误差在10%以内；3) 随着设计基准期T增大，偏差系数略微减小。

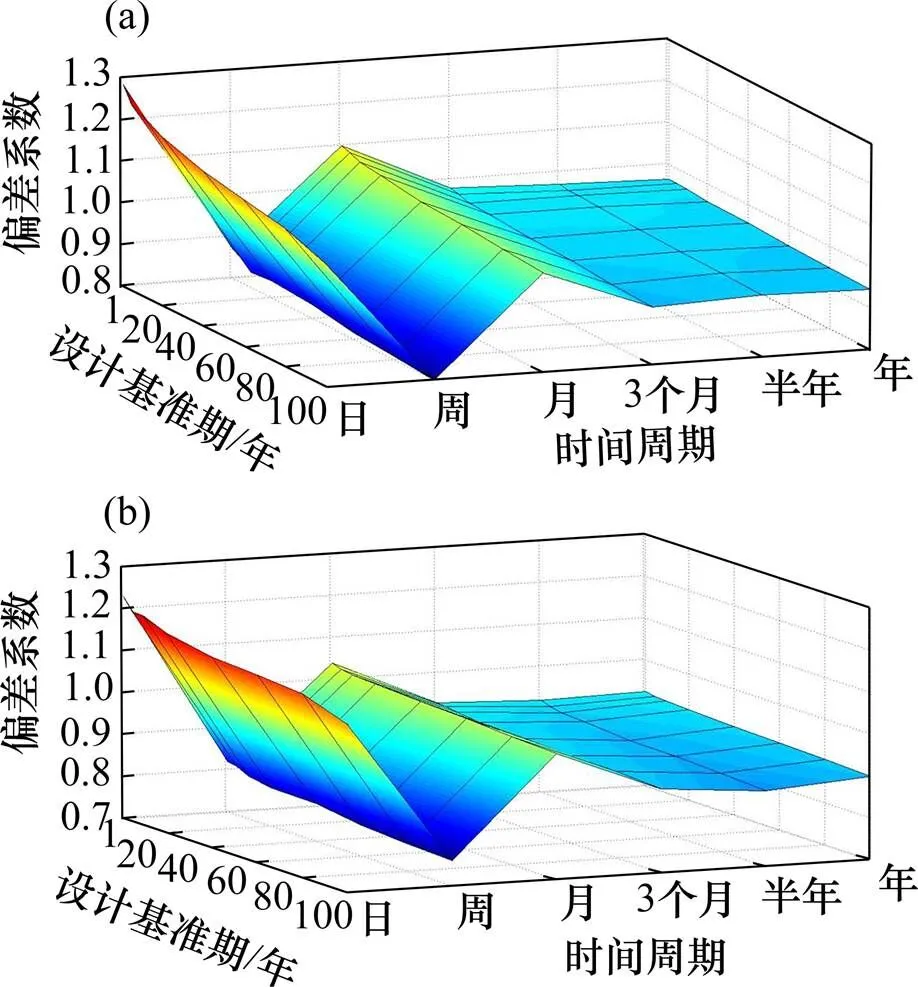
(a) 弯矩偏差系数；(b) 剪力偏差系数

《公路桥涵通用设计规范》JTG D60—2015的车道荷载采用集中力和均布力的组合模式，公路Ⅰ级均布荷载标准值为10.5 kN/m，集中荷载为360 kN。使用该组合荷载加载，取设计基准期为100 a对应的最大荷载效应概率分布0.95分位值即为荷载效应标准值。计算得到荷载效应标准值弯矩为10 439 kN·m，剪力为1 647 kN，随机车流作用下不同时间周期外推极值与规范荷载作用下的荷载效应标准值比值如表5所示。

表5 随机车流外推极值与规范荷载效应标准值比值

由表5可知：1) 随机车流作用下荷载效应极值均大于规范车辆荷载产生的荷载效应标准值，其中弯矩比值最大为1.44，剪力比值最大为1.78；2) 随着随机车流时间周期的增加，荷载效应比值逐渐减小，并趋于稳定。

5 结论

1) 受到重车/超载车辆的影响，行车道白天与夜间的车重均服从混合高斯分布，而超车道的白天与夜间车重均服从对数正态分布；白天夜间车头间距均服从对数正态分布。

2) 该随机车流模拟考虑了白天夜间2种时段车辆荷载的差异性，同时产生随机数的方式可以得到不同时间周期的随机车流，使随机车流更符合实际车辆运营状态，完善随机车流模型。

3) 随机车流作用下的荷载效应服从对数正态分布，用于极值外推的最大荷载效应服从极值I型分布；随机车流与实测车流作用下荷载效应外推极值相对误差在10%以内；根据不同时长编制的随机车流作用下的荷载效应外推值与规范对比，弯矩比值介于1.1到1.44，剪力比值介于1.16到1.78。

[1] JTG D60—2015, 公路桥涵设计通用规范[S]. JTG D60—2015, General code for design of highway bridges and culverts[S].

[2] Nowark A S, Nassif H. Live load models based on wim date[R]// New York: American Society of Civil Engineers, 2015.

[3] GU Y, LI S, LI H, et al. A novel bayesian extreme value distribution model of vehicle loads incorporating de-correlated tail fitting: Theory and application to the Nanjin 3rd Yangtze river bridge[J]. Engineering Structure, 2014(59): 386−392.

[4] Enright B, Obrien E J. Modeling same-direction two-lane traffic for bridge loading[J]. Structural Safety, 2011, 33 (4−5): 296−304.

[5] 宗周红, 杨泽刚, 夏叶飞, 等. 拥堵运行状态下新沂河大桥车辆荷载模型[J]. 中国公路学报, 2016, 29(2): 44−51. ZONG Zhouhong, YANG Zegang, XIA Yefei, et al. Vehicle load mocel for Xinyihe River Bridge under congested running status[J]. China Journal of Highway and Transport, 2016, 29(2): 44−51.

[6] 韩大章, 周军勇, 朱荣, 等. 基于计重收费数据的大跨径桥梁荷载效应评估[J].桥梁建设, 2018, 48(4): 27−32. HAN Dazhang, ZHOU Junyong, ZHU Rong, et al. Assessment of traffic load effects of long-span bridge based on toll-by-weight data[J]. Bridge Construction, 2018, 48(4): 27−32.

[7] 刘浪, 尤吉. 公路桥梁车辆荷载效应的外推计算[J]. 土木工程学报, 2015, 48(4): 59−64. LIU Lang, YOU Ji. Extrapolation method for truck effects on highway bridges[J]. China Civil Engineering Journal, 2015, 48(4): 59−64.

[8] 韩大千. 基于高速公路收费数据的交通流量分析[J]. 交通科学与工程, 2015, 31(4): 96−100. HAN Daqian. Analysis of traffic flow based on the toll data of the highway[J]. Journal of Transport Science and Engineering, 2015, 31(4): 96−100.

[9] Castillo E, Menéndez J M, Sánchez-Cambronero S, et al. A hierarchical optimization problem: Estimating traffic flow using Gamma random variables in a Bayesian context[J]. Computers & Operations Research, 2014(41): 240−251.

[10] 田苾, 黄健陵, 陈辉华, 等. 基于贝叶斯网络的邻近既有线施工风险分析[J]. 铁道科学与工程学报, 2018, 15(8): 2163−2171. TIAN Bi, HUANG Jianling, CHEN Huihua, et al. The BN-based risk analysis of railway construction close to existing line[J]. Journal of Railway Engineering Society, 2018, 15(8): 2163−2171.

[11] Obrien E J, Enright B. Using Weigh-in-motion data to determine aggressiveness of traffic for bridge loading[J]. Journal of Bridge Engineering, 2013,18(3): 232−239.

[12] RUAN X, ZHOU J, Caprani C. Safety assessment of the antisliding between the main cable and middle saddle of a three-pylon suspension bridge considering traffic load modeling[J]. Journal of Bridge Engineering, 2016, 21(10): 04016069.

[13] Obrien E, Bordallo-Ruiz A, Enright B. Lifetime maximumload effects on short-span bridges subject tgrowing traffic volumes[J]. Structural Safety, 2014, 50: 113−122.

[14] 王贵春, 孙瑜祥, 张杰, 等. 车队作用下曲线连续梁桥动力响应分析[J]. 铁道科学与工程学报, 2019, 16(6): 1476−1483. WANG Guichun, SUN Yuxiang, ZHANG Jie, et al. The analysis on dynamic responses of curved continuous bridge due to vehicle flow[J]. Journal of Railway Science and Engineering , 2019, 16(6): 1476−1483.

[15] 王贵春, 张校卫. 考虑车辆运行参数变化的悬索桥车激振动分析[J]. 铁道科学与工程学报, 2017, 14(7): 1442−1448. WANG Guichun, ZHANG Xiaowei. The analysis on vehicle-excited vibration of suspension bridge considering variation of vehicle operational parameters[J]. Journal of Railway Science and Engineering, 2017, 14(7): 1442−1448.

[16] 阮欣, 周军勇, 石雪飞. 桥梁汽车荷载响应的极值外推方法综述[J]. 同济大学学报(自然科学版), 2015, 43(9): 1339−1346. RUAN Xin, ZHOU Junyong, SHI Xuefei. Review on extreme extrapolation methods for bridge traffic load response[J]. Journal of Tongji University (Natural Science), 2015, 43(9): 1339−1346.

[17] 李整, 陈代海, 陈淮. 中小流域桥梁设计与检定流量计算方法研究[J]. 铁道科学与工程学报, 2016, 13(1): 111−116. LI Zheng, CHEN Daihai, CHEN Huai. Research on design flow and check flow calculation method for bridges in small and medium watersheds[J]. Journal of Railway Science and Engineering, 2016, 13(1): 111−116.

Load effect analysis of traffic flow in different periods

ZHANG Ming1, KONG Yandong2, LIU Yang1, LU Naiwei1, YIN Xinfeng1, YAN Wei1, 3

(1. School of Civil Engineering，Changsha University of Science & Technology, Changsha 410114, China;2. Shaoxing Station of Traffic Engineering Quality and Safety Supervision, Shaoxing 312000, China;3. China Highway Engineering Consultants Corporation, Wuhan 430040, China)

In order to study the effect of vehicle operation on load effect in different periods, based on the measured data of more than 1 million WIMs of Nanxi Changjiang River Bridge, the vehicle load parameters in day and night were calculated and a stochastic vehicle load model was established. The time-division traffic load effect of the three-span continuous beam bridge was studied, and the extrapolated extremum in the design reference period was compared with the design specification. The research shows that the day and night vehicle weights of lanes obey the mixed Gaussian distribution and the day and night vehicle weights of overtaking lanes obey the lognormal distribution under the influence of overloaded vehicles; the headway distance during the day and night obey the lognormal distributed; The load effect of bridges under random traffic flow obeys lognormal distribution, and the maximum load effect for extremum extrapolation obeys extreme I distribution; The relative error of extreme value extrapolated from load effect under random traffic flow and measured vehicle flow is less than 10%; The extrapolation value of load effect under the random traffic flow at different time is greater than the standard value.

highway bridge; vehicle loads model; live load effect; extreme value extrapolation; stochastic process