基于混沌多项式的指令鲁棒优化及在飞行控制中的应用

曹 瑞，沈海东，刘燕斌 ，陆宇平

(1.南京航空航天大学自动化学院，江苏南京 211106;2.南京航空航天大学航天学院，江苏南京 210016)

1 引言

在实践中，通常会存在由于测量误差、缺乏相关的操纵知识、或者无法达到某些参数的测量条件使得参数无法测量的情况.特别是对于行星着陆器和高超声速飞行器，由于环境未知以及系统间耦合无法完全表述等原因，导致系统不完全可知.如果不考虑系统存在的不确定性进行轨迹和控制设计可能对任务产生不利后果.因此，必须在计算过程中对不确定性进行适当的处理，以便能够充分了解参数、初始条件或边界条件中误差或不确定带来的影响.针对随机系统，为了获得可靠的预测结果或使预测误差最小，人们付出大量的努力研究不确定系统分析和预测算法.对于非线性动力系统，蒙特卡罗(Monte-Carlo，MC)[1]、马尔科夫链[2]、局部线性化、无迹卡尔曼滤波[3]、Fokker-Planck-Kolmogorov框架[4]、混沌多项式和细胞间映射[5]等方法可以用于量化由随机变量引起的状态不确定性.

其中，混沌多项式(polynomial chaos，PC)是最有前途的不确定量化方法之一.与MC方法相比，PC 方法具有计算量小、精度高等优点.MC方法因其相对简单而广受欢迎，通常是分析此类随机问题优先考虑的方法.但是MC方法为获得高精度计算结果，所需要的重复过程会带来非常大的计算负担.此外，MC方法在计算上是不可伸缩的，并且可能出现统计上的不一致.PC方法提供的从随机问题到确定性问题的转换方案，由于其准确性和计算效率，在随机系统轨迹优化的背景下十分具有吸引力.Norbert Wiener[6]提出了Hermite齐次混沌理论，其基于随机变量的概率分布特性，结合正交多项式将不确定方程转化为一组增广的确定方程.之后，Ghanem和Spanos[7]对该理论进行改进，克服了应用于非高斯随机系统时先验的收敛性问题，并将其应用于许多实际系统的不确定性量化.研究表明，只有根据随机变量的概率分布选择适当的正交多项式，才能实现完全收敛[8].选择合适的正交基之后，需要使用Galerkin投影[9]或随机配置[10]进一步解决原随机系统的不确定量化问题.Galerkin投影法可以采用比随机配置方法更少的方程数目，实现对随机模型的准确预测[11]，因此被广泛使用.Galerkin投影法利用投影原理，最小化基于混沌多项式的估计系统和原随机系统之间的误差，从而产生了一组增广的确定方程.之后，可以使用欧拉方程或龙格-库塔方程对增广系统进行求解，进而预测不确定系统的运动学特性.然而，不确定量化的实现过程并不像Galerkin投影那样简单明了.这对于复杂的非线性应用来说仍是一个具有挑战性的过程[12].混沌多项式方法最早由Wiener[6]引入，他使用Hermite多项式对具有高斯分布变量的随机过程进行模拟.根据Cameron和Martin[13]研究得知，基于混沌多项式的扩展在L2意义下可以收敛于任何具有有限方差的随机过程，这适用于大多数的物理系统.Liu和Zhang[14]使用来自Askey方案[15]的正交多项式将Martin的结果推广到各种连续和离散的分布中，并证明L2在相应的Hilbert泛函空间中收敛.通常将其称为广义PC(generalized PC，gPC)方法.gPC方法已经应用于各个学科之中，包括飞行器轨迹优化、翼型设计[16-17]、代理模型[18]和参数敏感性研究[19]等.

虽然gPC方法广泛应用于系统分析和轨迹优化之中，但很少将其应用于飞行器控制指令优化设计.在控制环境下，gPC 应用的发展主要归功于Nagy 和Braatz，他们在工业应用中证明了参数不确定对非线性系统的影响[20].但是，工业中的应用是一个验证技术，并没有对稳定性进行分析.文献[21]将gPC应用于简单的悬停和飞行双线性系统中，主要用于分析系统在不确定下的稳定性.2010 年，Prabhakar等人[22]首次使用gPC演示了一种用于高超声速飞行器的新型不确定性传播框架.之后，Dutta和Bhattacharya[23]对随机过程的先验概率密度函数(probability density function，PDF)进行贝叶斯估计，从而对这项工作进行了扩展.与线性估计器相比，贝叶斯估计器和gPC的组合在非线性高超声速飞行器不确定性分析问题上取得了很好的表现.在gPC随机框架中，目标函数如何设计十分重要，通常采用随机参数的期望或方差作为目标函数.Bhattacharya和Fisher[24]在2011年对此进行了研究，他们证明了gPC随机框架中的目标函数等价于标准的二次目标函数.Xiong等人[25]也证明了这一点，并且他们将这些优化原则应用于超敏问题和范德波尔问题.上述例子均是对单变量随机系统(参数或初始条件不确定)的分析或设计，虽然Xiong等人[26]对系统存在多元、混合分布随机变量的问题进行了讨论，但不在优化的范围内.

因此，本文基于gPC方法对多维、混合分布随机系统分析和飞行器控制指令优化设计应用方面进行研究.通过gPC方法将随机系统转换为增广的确定系统，并设计合适的目标函数，生成一个增广的最优控制问题(augmented optimal control problem，AOCP).通 过求解该最优控制问题，从而获得具有鲁棒特性的优化控制指令.优化求解方法通常包括直接和间接两种方法.间接方法利用庞特里亚金原理，从最小化哈密顿能量的角度来阐述问题.直接方法将最优控制问题转化为有限维非线性规划问题[27].与间接法相比，直接法易于使用，因此被广泛采用.本文利用gPC方法将多维、混合分布随机系统分析，不确定性预测分析与优化控制相结合，在考虑结构不确定性的情况下获得鲁棒性更强的优化控制方案，扩展了前人在该领域的工作.

本文首先介绍混沌多项式扩展方法，描述如何通过混沌多项式对随机信息进行数学表述;并利用Galerkin投影法将随机变量的混沌多项式引入常微分方程中.然后，将随机变量的均值和方差考虑至优化问题的成本函数中，并利用伪谱方法对控制指令进行鲁棒优化.最后，通过仿真验证了本文所提方法在控制指令设计上的有效性，并对存在一维随机变量和多维、混合分布随机变量的系统进行分析.仿真结果表明该方法计算效率高、精度高，并且生成的控制指令对存在参数或初始条件不确定的系统具有很好的鲁棒性.

2 基于混沌多项式的控制指令优化方法

在本节中，基于混沌多项式扩展法和Galerkin投影法，对随机动力学系统转换为高维空间中的等效确定动力学系统的过程进行介绍.并将上述方法应用于最优控制，生成考虑系统不确定性的鲁棒优化控制方案.

2.1 随机系统的混沌多项式扩展方法

2.1.1 混沌多项式

其中:ω为随机事件，φi[Δ(ω)]表示随机变量Δ(ω)的第i个gPC基函数.函数φ是L2(Ω，F，)上的正交基，满足式(2)所示的关系式:

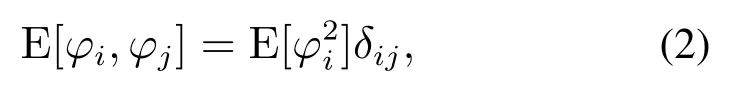
其中:δij=0，i/=j;δij=1，i=j;E[·]表示概率测度d(ω)=ρ[Δ(ω)]dω的期望，其中ρ[Δ(ω)]为概率密度函数.之后，采用Δ代表Δ(ω).对于随机变量Δ，可以根据其概率分布选择合适的正交基函数φ，使其权函数的形式与概率密度函数ρ(Δ)相同.这些正交多项式属于Askey多项式[15];在希尔伯特空间中，由它们构成了完备基.表1总结了Δ概率分布函数与相对应多项式之间的关系[28].

表1 基于随机变量PDF的正交多项式选取Table 1 Orthogonal polynomial selection based on PDF of stochastic variable

2.1.2 基于Galerkin投影引入随机信息

本节描述了一个形式为˙x=f(x，Δ)的随机系统采用PC框架转换为高维空间中等效确定系统的过程，其中:x∈Rn，Δ ∈Rd，n为系统维数，d为随机变量数目.假设随机微分方程的解为x(t，Δ)，则对于n阶系统，x ∈Rn中每个分量可近似表达为式(3)所示形式:

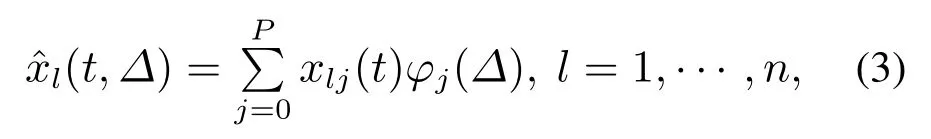
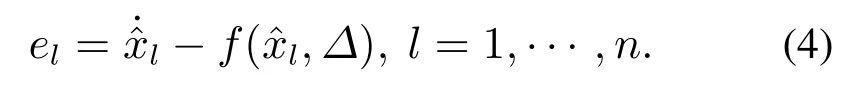
通过执行Galerkin投影，将误差el设置为零，可以获得最优的动力学系统近似方程

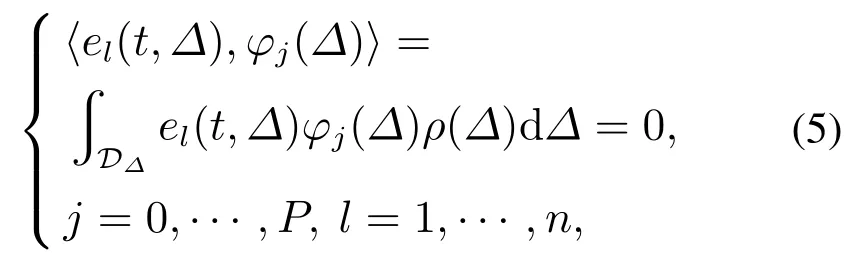
其中:DΔ为Δ的定义域;ρ为随机变量Δ的概率密度分布函数.结合式(4)-(5)获得的n(P +1)维确定性常微分方程，然后通过数值求解得到随机系统的近似响应.

基于上述流程实现了将Rn中的随机动力学方程转化为Rn(P+1)中的确定动力学方程.式(5)中正交多项式φ的阶数P由随机变量Δ的维数d和运动方程阶数r决定，满足如下条件:

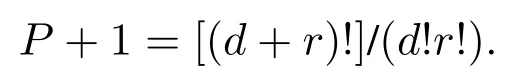
该表达式给出了具有d个随机变量，最高阶为r的随机系统进行不确定量化所需的混沌正交多项式项数.下面以一阶线性系统(6)为例，对这一理论的应用进行展示:

其中a为均匀分布于[0，1]的随机变量.

根据表1可以看出，随机变量a概率分布所对应的混沌正交基函数是勒让德(Legendre)多项式.由于勒让德多项式的定义域为[-1，1]，因此，需要将随机变量a转换为a=-0.5+0.5Δ的形式，且Δ ∈[-1，1];则随机变量a的混沌多项展开式如式(7)所示:

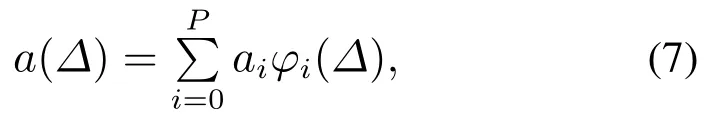
其中:φi为随机变量a对应的第i阶正交基函数;ai为第i阶正交基函数对应的系数.

在一阶线性系统中，式(3)和式(4)的具体表达形式分别如式(8)和式(9)所示:

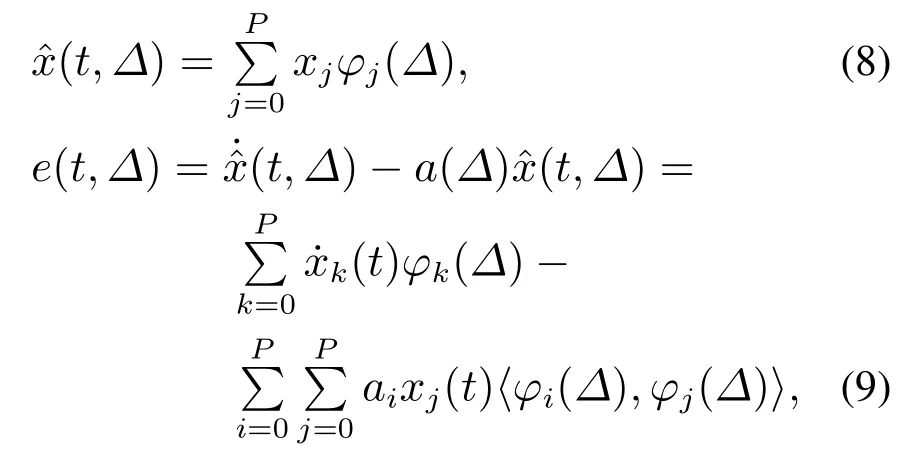
其中:φj为的第j阶正交基函数;xj为第j阶正交基函数对应的系数;φk为的第k阶正交基函数;为第k阶正交基函数对应的系数.

将e(t，Δ)投影到φk上并将其设为0，可以得到式(10):

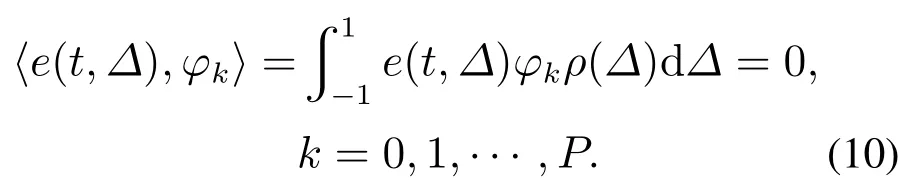
根据式(10)可以得到

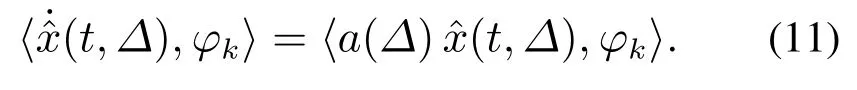
对式(11)进一步展开可以获得

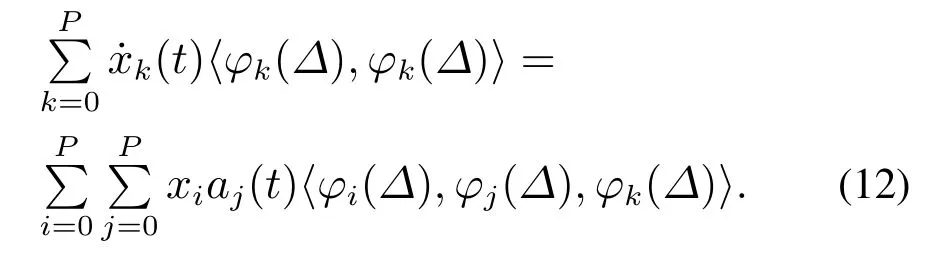
由于φ是正交函数，所以式(12)可以进一步简化为如下形式:

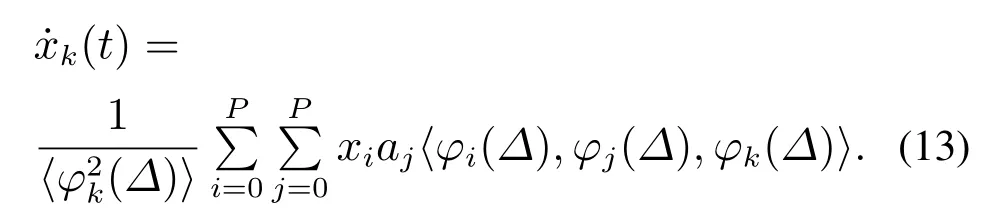
对式(13)进行改写，将其转换为如下表达式:

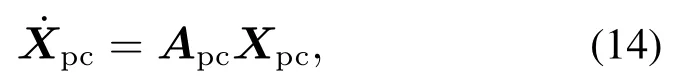
矩阵Apc∈R(P+1)×(P+1)由式(13)确定，并且Xpc=[x0x1··· xP]T为不确定量化后增广矩阵多对应的状态量.

上述过程完成了随机方程x(t，Δ)∈R向确定方程Xpc(t)∈R(P+1)的转化，进而可以采用常微分方程的标准数值算法进行求解.文献[29]推导了线性动力学x(t，Δ)∈R的广义表达式，并证明了这种变换在动力学中也保持线性关系.

2.1.3 多维不确定性描述

考虑系统存在多维、混合分布随机变量的情况，如果它们是相互独立的，则PDF为每个随机变量概率密度分布函数的乘积.因此，即使在混合分布情况下，也可以很好地捕捉系统特性.下面对多维、混合分布随机系统的混沌多项展开式(polynomial chaos expansion，PCE)建立过程进行简单介绍.假设随机变量初始的PCE系数a由均值µa和方差δa组成.对于仅包含参数不确定性的问题，随机参数的均值和标准差分别置于第1项和第2项，其他值均为零.并且，其PCE系数的维数为P +1，则a=[µaδa0···0]P+1.但是，在多维的情况下，情况略有不同(下面将详细描述).若采用符号eijk表示式(12)中的三重变量积分，采用γk表示归一化因子(Δ)，则不确定量化后的增广系统可以采用式(15)进行表示:

其中:

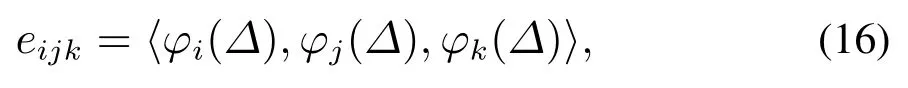
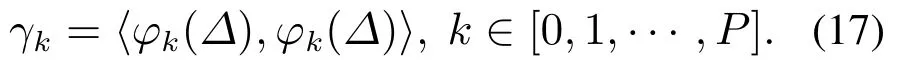
下面以具有两个不确定量的三阶线性系统为例，介绍多维、混合分布随机系统的不确定量化过程.假设两个随机变量Δ1和Δ2的概率密度函数分别为高斯分布和均匀分布.然后，针对变量Δ1和Δ2分别应用埃尔米特(Hermite)和勒让德正交多项式，计算对应的三重积分eijk和归一化因子γk，其具体表达形式如下所示:

其中:s表示正交条件，满足式(20)所示形式;N+表示整数集.

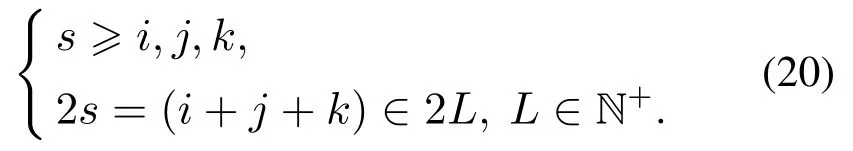
除了采用式(18)和式(19)所示的表达式求解eijk，也可以采用积分方法进行求解.若仅考虑一个随机变量，则多项式的阶数由下标i，j，k给出.若考虑多维随机变量，多项式基函数可以通过分级顺序索引方法[4]进行建立.该方法将生成维数为[(P +1)×d]的索引数组，例如:考虑一个具有两个不确定量(d=2)的三阶系统(n=3)混沌多项式扩展问题.表2展示了使用上述方法所建立的多维、混合分布随机系统的多项式正交基，其中:φ的下标对应基函数的阶数;Δ的下标与随机变量相对应.

表2中多级引索因子α决定了随机变量Δ1和Δ2均值µ(Δ)和方差δ(Δ)在初始PCE系数中的位置.根据表2可得随机变量Δ1和Δ2初始PCE系数分别为

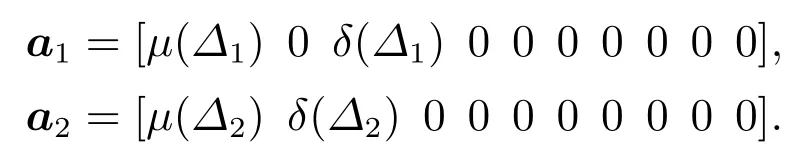
对于随机变量采用埃尔米特多项式或勒让德多项式进行展开.随机系统归一化因子γk的表达式分别如式(21)和式(22)所示:

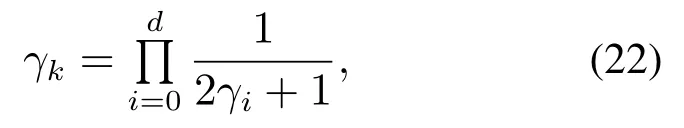
其中γi为第i个随机变量的归一化因子.

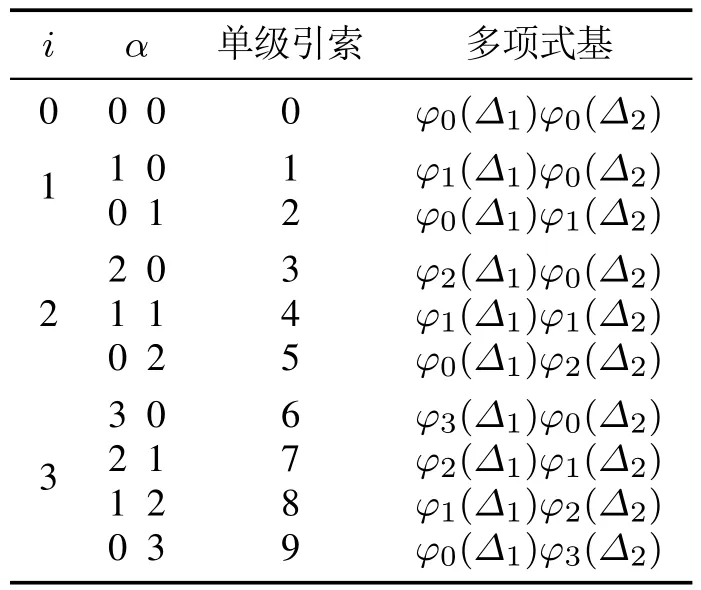
表2 n=3，d=2的多级引索方法Table 2 Multi-index method for n=3，d=2

根据式(21)-(22)可知，若随机系统中多维不确定变量相互独立，则该系统的归一化因子γk为各不确定变量对应归一化因子的乘积.然后结合方程(13)，可以获得不确定量化后的增广矩阵A.考虑式(23)所示的连续时间线性系统，其存在一个受参数b影响的控制输入u.

LTI:

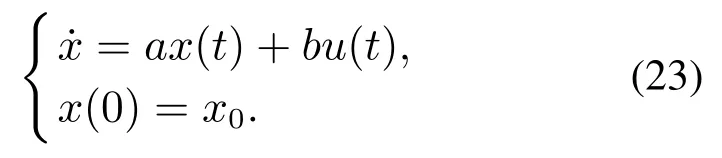
假设变量x为随机变量(上述线性系统中的参数a和初始条件x0均为不确定参数)，控制变量是确定值，即b是常数.则对随机系统(23)进行不确定量化，获得的增广线性系统可由式(24)给出:

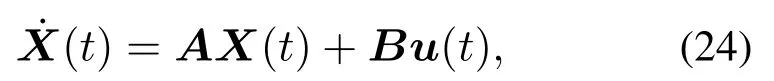
其中:状态向量定义为X=[x0x1··· xp1]T，控制向量定义为u=ns为随机系统维数;p2=nc(P +1)，nc为控制输入维数.状态转换矩阵第k行，第j列元素的表达式如式(25)所示:

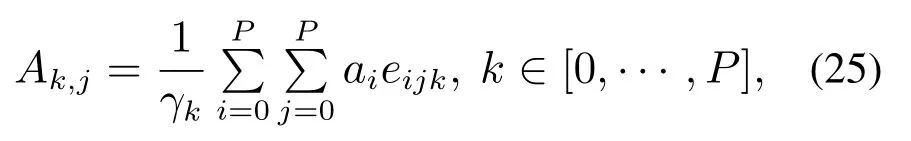
其中ai定义同式(7)一致.假设参数b=1，即系统中控制参数确定，则相应增广系统的控制矩阵为B=[1 0··· 0]T，其维数为其中PCE系数由式(24)中状态向量X的各分量表示.若系统初始条件不确定，则式(24)中的状态初始向量为X0=[µxδx0··· 0]T;若仅参数a存在不确定性，初始条件确定，则X0中仅存在µx这一非零项.下面将介绍如何将获得的增广矩阵用于控制优化设计，以充分利用已知的不确定性信息.

2.2 随机系统最优控制指令设计

对于一个随机系统，为获得考虑系统不确定性的最优控制指令u*，必须对原成本函数进行修正.对于不确定系统控制优化，需要将不确定参数的信息(均值和方差)考虑到成本函数中.不确定参数的信息可以使用混沌多项式和Galerkin投影法产生增广系统的状态进行描述.在PC框架中，均值和标准差定义为

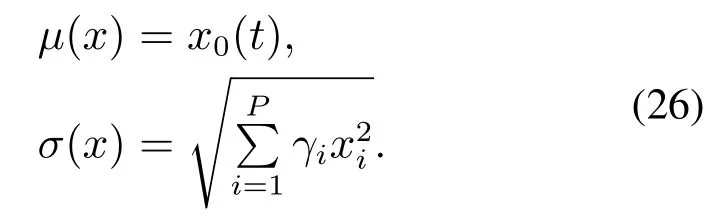
根据上述定义可知，不确定参数的均值总是对应于增广系统的第1个状态x0，而方差是归一化因子与增广系统其他状态平方乘积的和.因此，考虑不确定性的增广最优控制问题可以通过下式进行描述:

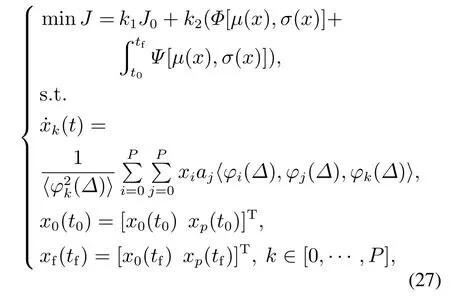
其中:J0表示与随机变量无关的性能指标;Φ[µ(x)，σ(x)]表示终端优化形式，目的是使随机变量在轨迹末端的变化最小;表示积分优化形式，目的是最小化整个任务段随机变量的均值或方差. k1和k2分别为J0和随机变量统计信息的权重值.

例如，若希望最小化最终期望值，则可以将式(28)所表示的随机系统期望项写入成本函数中.

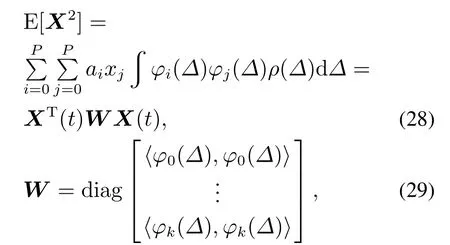
其中:W表示由归一化因子组成的权重矩阵;X表示增广矩阵的状态量.

若期望最小化最终方差，则可以将式(30)所表示的随机系统方差项写入成本函数中.

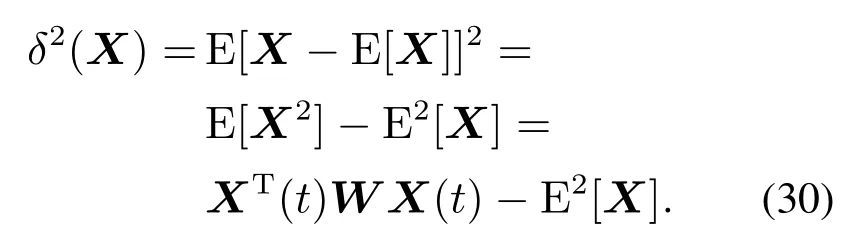
由于不确定参数的均值总是对应于增广系统的第1个状态，因此

故，可以将式(30)进一步简化为

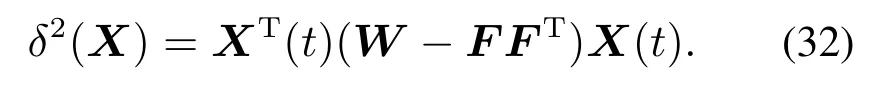
因此，可以对式(28)(32)进行积分，以积分形式考虑在成本函数中或直接设置为终端条件.然后求解式(27)所示的优化问题获得随机系统的鲁棒优化控制指令信号.下面将概述随机系统控制指令鲁棒优化设计过程.最后通过仿真，介绍增广系统的设计过程，并验证基于混沌多项式的控制指令鲁棒优化设计的有效性.

提出的随机系统控制指令鲁棒优化方案可归纳为以下步骤，其实现流程如图1所示，其中各随机变量相应的混沌正交基的初始阶数由P0=(d+r)!/(d!r!)-1确定.

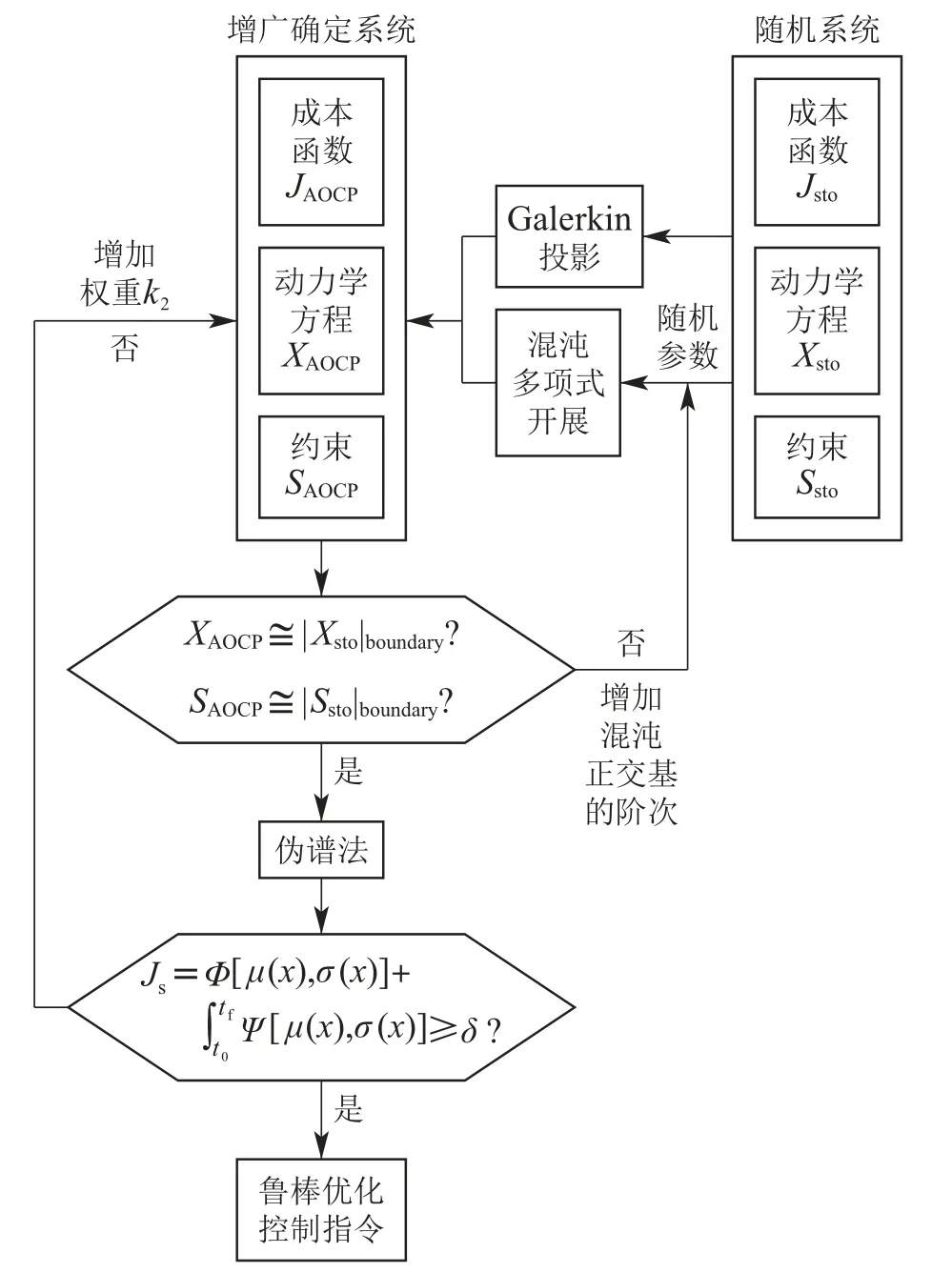
图1 基于混沌多项式的控制指令鲁棒优化方案Fig.1 Control command robust optimization strategy based on polynomial chaos

步骤1为系统中各随机变量设置相应的混沌多项展开式，并根据第2.1.3节所示内容建立多级引索，进而获取多维、混合分布随机系统的多项式正交基;

步骤2根据Galerkin投影法将随机动力学方程Xsto转换为等价的增广确定性模型XAOCP;

步骤3根据Galerkin投影法将随机约束条件Ssto转换为增广的确定性等价约束SAOCP;

步骤4根据最小期望/协方差对随机成本函数进行量化，根据式(27)所示成本函数形式将随机系统成本函数Jsto转为增广确定系统的成本函数JAOCP;

步骤5判断增广系统的运动学模型XAOCP以及约束条件SAOCP是否满足可以近似描述随机系统动力学方程不确定边界|Xsto|boundary和约束条件不确定边界|Ssto|boundary的要求.若满足，则进入步骤6;若不满足，则增加混沌正交基的阶数并返回步骤1;

步骤6通过伪谱法对增广系统的优化问题(27)进行求解;

步骤7判断成本函数中随机量的统计信息Js是否小于设定值δ(人为设定).若满足，则获得具有鲁棒性的最优控制指令;否则对成本函数JAOCP中随机信息统计量对应的权重值k2进行调整，并返回步骤6.

3 随机系统鲁棒优化方法仿真示例

在此考虑一个简单非线性系统，不考虑系统存在不确定时，其标称系统的优化控制问题描述如下所示:

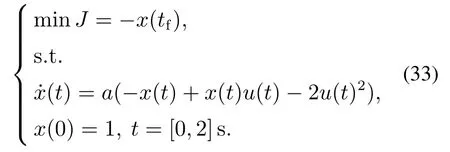
考虑系统存在两个随机变量:参数a概率分布满足正态分布a～N(2.5，0.1);初始状态量x0的概率分布满足均匀分布x0～U(0.9，1.1).根据式(33)可以看出，此非线性系统的控制输入也受到随机变量的影响.

首先考虑仅存在参数a不确定的情况，参数a的初始PCE系数为ai=[2.5 0.1 0]，增广系统的初始条件为X0=[1 0 0]T，则增广系统如式(34)所示.该增广系统最优控制问题的目标函数设置为式(35)所示结构

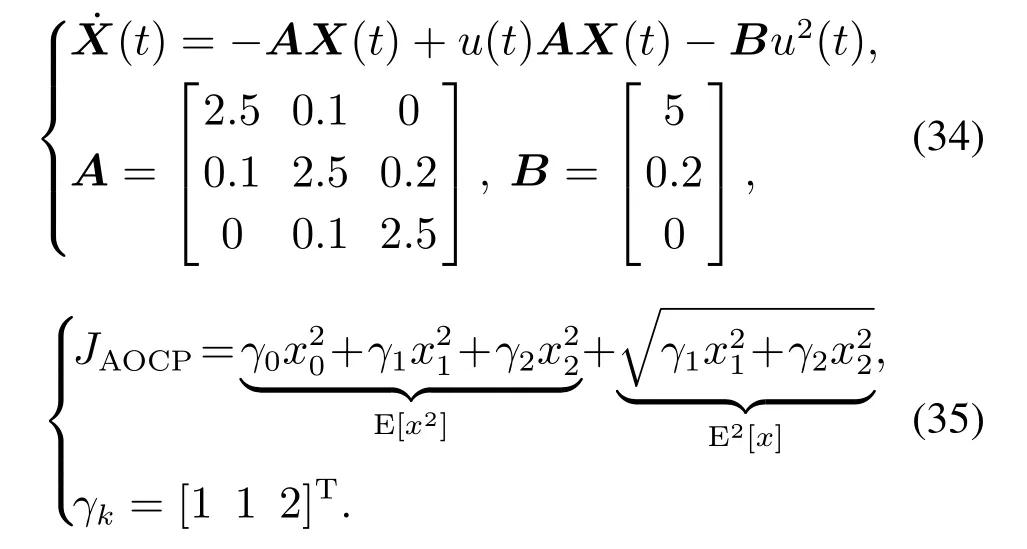
在标称系统下求解优化控制问题(33)所得的控制指令记为CJ;在随机系统下基于混沌多项式鲁棒优化方法生成的控制指令记为CJAOCP，其控制输入和对应的增广系统状态分别如图2(a)-2(b)所示.

根据图2(b)可知，在控制指令CJAOCP作用下增广系统状态随时间逐渐收敛于零.

将CJ和CJAOCP分别作用于随机系统进行1000次蒙特卡罗分析，以验证基于混沌多项式的控制指令鲁棒优化方案的有效性.图3展示的MC仿真结果证明了本文所提方法可以有效利用已知的不确定信息，生成对不确定性有抑制作用的控制指令.

图2 控制量和PCE系数变化曲线Fig.2 Change curve of control and PCE coefficients

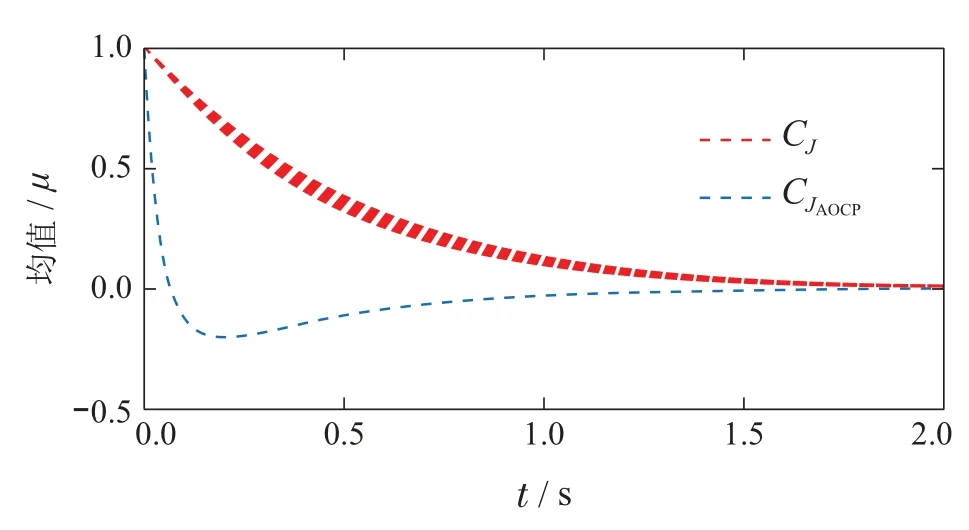
图3 一维不确定性系统MC分析Fig.3 MC analysis for one dimensional uncertainty system

然后考虑参数a和初始状态x0不确定的情况，根据第2.1.3节内容对随机系统进行不确定量化，以获得式(36)所示的增广矩阵;其中，参数a的初始PCE系数、增广系统初始状态和归一化因子分别为

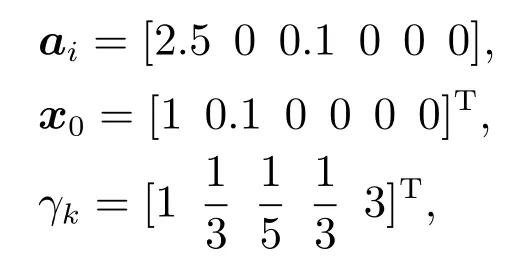
图4(a)展示了二维不确定情况、一维不确定情况以及标称情况下的控制曲线;图4(b)展示了二维不确定情况下的增广系统状态变化图.图5展示了CJ和二维不确定系统优化控制指令CJAOCP分别作用于随机系统进行1000次蒙特卡罗仿真的结果.

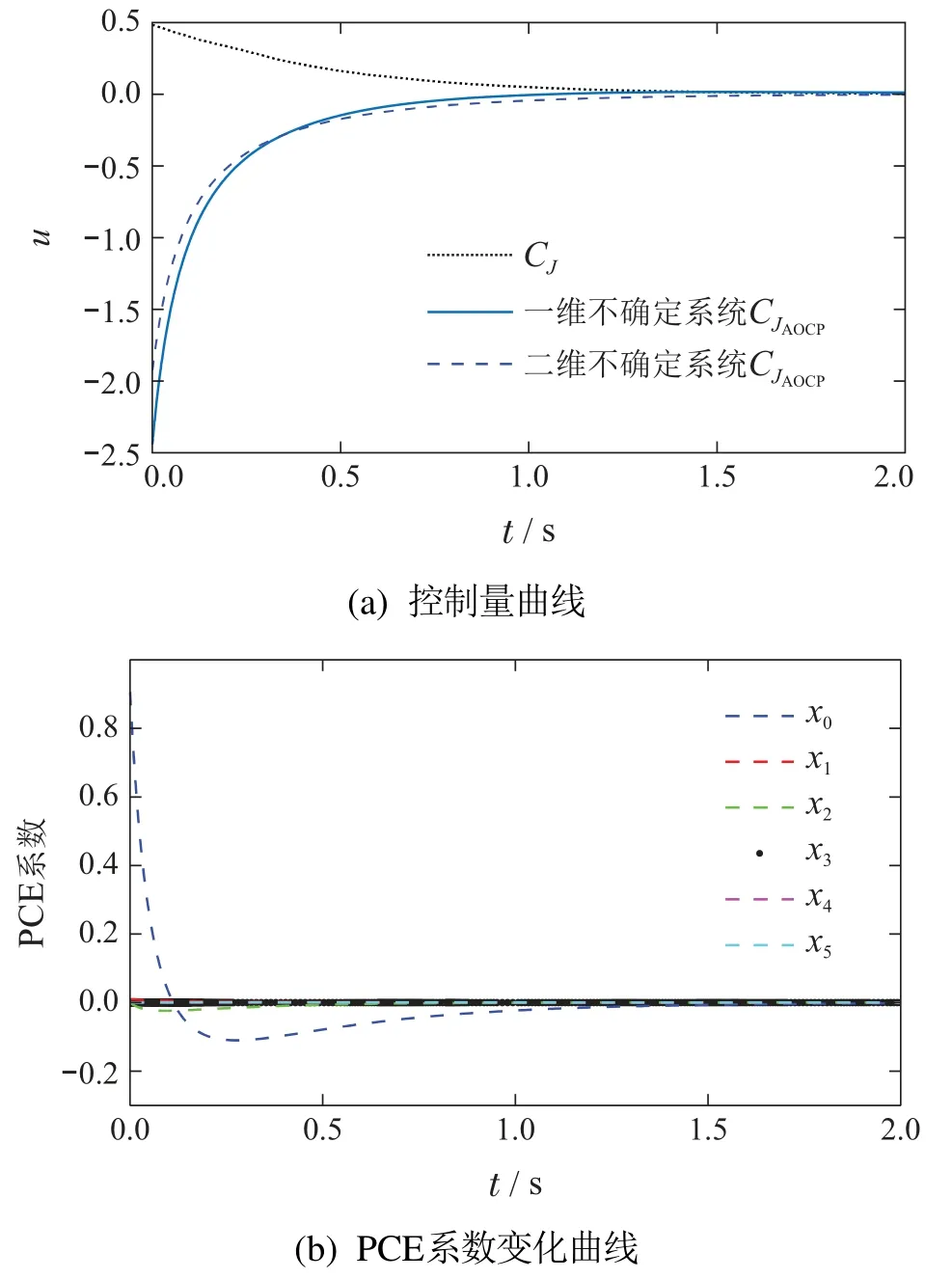
图4 控制量和PCE系数变化曲线Fig.4 Change curve of control and PCE coefficients

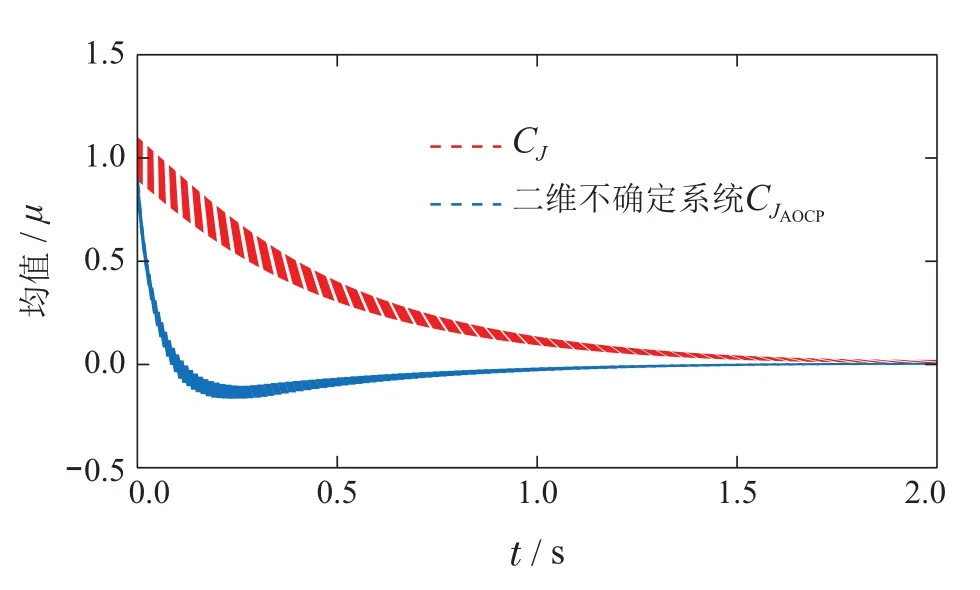
图5 二维不确定性系统MC分析Fig.5 MC analysis for two dimensional uncertainty system

根据图3和图5的仿真结果可知:虽然随机初始条件会对系统变化带来非常明显影响，但是基于混沌多项式的鲁棒优化方法生成的控制指令仍然具有良好的不确定抑制效果.本节以非线性系统为例，详细介绍基于混沌多项式的鲁棒优化方法对随机系统控制指令的优化设计过程，并仿真验证所提方案的有效性.下节将介绍本文所提方法在飞行控制中的应用.

4 飞行控制中的分析应用

4.1 随机系统运动学特性预测

本节考虑F-16飞行器模型存在参数不确定性，分析本文所提方法获取的增广系统对随机系统运动学特性的预测性能.为简单起见，假设系统参数变化依赖于单个随机变量Δ.在这个例子中，考虑了F-16飞行器短周期近似模型，该模型由文献[30]给出.

其中状态向量为x=[α q xe]T，α是迎角，q为俯仰角速率，xe为所测量的升降舵状态.控制输入u=δec是升降舵指令，单位为度.飞行器模型中各矩阵数值如下所示:

假设括号内的参数是不确定的，并且其概率分布满足均匀分布特点，与其标称值有20%的偏差.这种不确定性是由于阻尼项Cxq不确定性所引起的;Cxq在大迎角条件下很难建立准确模型.文献[31]设计了一种基于俯仰角速率q反馈的频域控制(控制律在标称系统上进行设计)，控制器的表达形式如下所示:

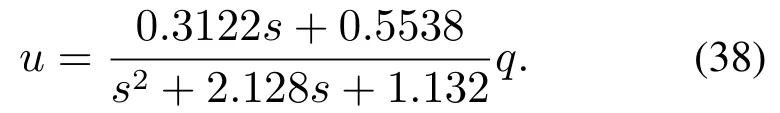
式(38)表示一种俯仰角速率反馈控制器.将上述表达式转换为状态空间形式(Ac，Bc，Cc)并对原系统进行增广，得到闭环系统

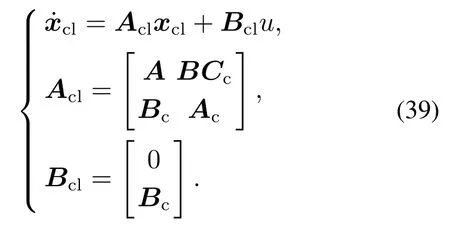
图6和图7展示了本文所提方法获取的增广系统对随机系统(39)动力学特性的预测能力.图6中的圆表示混沌增广系统的特征值，实点代表对随机系统(39)进行蒙特卡罗仿真所得到的系统特征值.

图7显示了上述参数中存在±20%不确定性时系统的俯仰角速率响应.由PC所预测的俯仰角速率曲线和通过蒙特卡罗仿真获得的俯仰角速率曲线分别由虚线和暗实线表示.

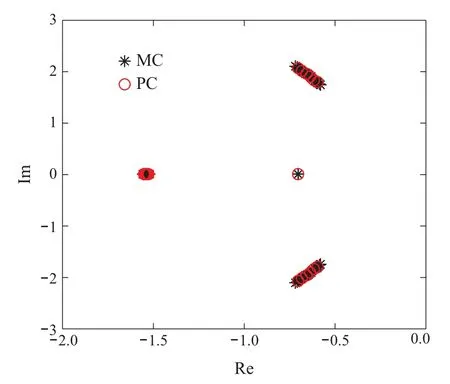
图6 ±20%参数不确定性的短周期闭环特征值分布Fig.6 Closed loop eigenvalue distributions for a short-period mode for±20%parameter uncertainty

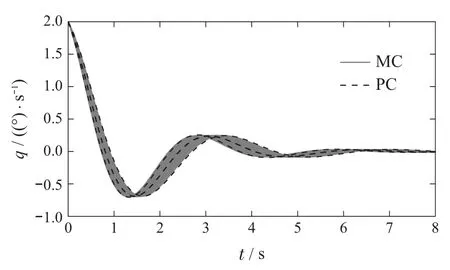
图7 PC和MC系统对±20%参数不确定性的响应Fig.7 PC and MC system response to±20%parameter uncertainty

从图6可以得知，混沌增广系统捕捉到了随机系统的特征值分布.根据图7可以得知，PC系统预测的边界与MC仿真曲线边界十分一致.此仿真结果表明:获得的增广系统可以用于预测随机系统运动学特性以及分析随机系统稳定性，并且这种方法比MC方法更有效，计算效率更高.

4.2 控制指令的鲁棒优化设计

F-16飞行器系统的不确定参数满足均匀分布的特点，与其标称值存在±20%的偏差，其不确定量化后的增广矩阵A由表示.然后，根据第2.2节提出的控制指令优化方案对增广后系统的控制指令进行鲁棒优化设计，并与文献[31]所提鲁棒控制器和式(38)所示控制器作用到原不确定系统中进行仿真，并对仿真结果进行对比.

由于是对飞行控制系统进行控制器设计，因此需要考虑控制输入的饱和约束.

在此设计除去配平舵面需求外，满足额外控制需求的舵面约束为δec∈[-8°，8°].根据图7可知控制器(38)对不确定抑制能力弱，因此在图8中仅展示了不确定系统在多胞鲁棒控制器[31]、基于混沌多项式的鲁棒优化控制指令下，仿真获得的控制输入和根据式(27)计算所得性能指标对比结果.

最后，将多胞鲁棒控制器[31]、基于混沌多项式的鲁棒优化控制指令和控制器(38)作用到随机系统(37)中进行蒙特卡罗仿真，其仿真对比结果如图9所示.然后考虑存在参数和初始状态不确定情况下，分析基于上述控制指令的控制效果.假设俯仰角速率的随机初始状态满足正态分布q0～N(2，0.25)，在参数和初始状态不确定条件下的蒙特卡罗仿真和性能指标对比结果如图10所示.

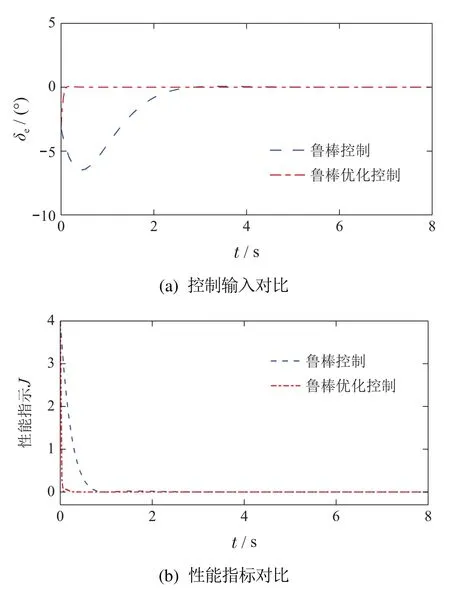
图8 两种控制算法下控制输入与性能指标Fig.8 Control input and performance indicator of two control algorithms

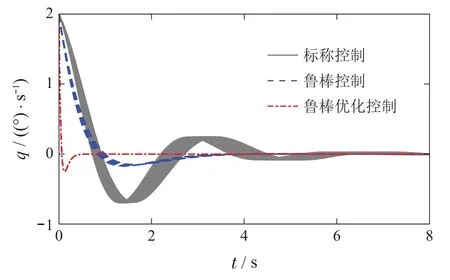
图9 单维不确定系统MC分析Fig.9 MC analysis for single-dimensional uncertainty system

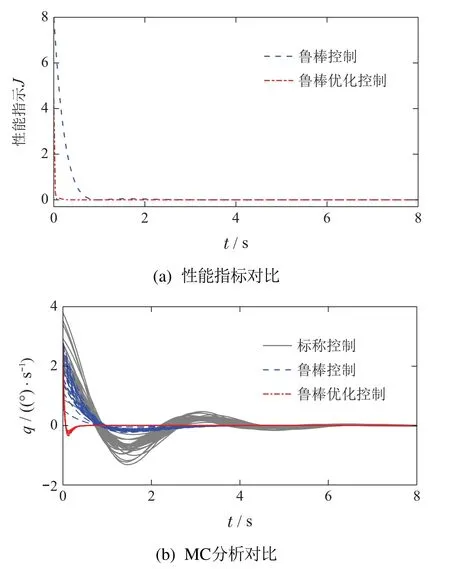
图10 性能指标以及多维、混合分布不确定系统的MC分析Fig.10 Performance indicator and MC analysis for multi-dimensional，mixed-distribution uncertainty system

根据图8-10的仿真结果，可以看出本文提出的方法可以充分利用系统中不确定参数信息，其优化产生的控制指令比鲁棒控制律在不确定性抑制方面具有更好的性能.根据图8可以得出本文提出的鲁棒优化方法与文献[31]中的鲁棒控制器相比，可以在有效抑制系统不确定性的基础上降低所需的控制能量.根据图10可以得知，本文提出的方法对存在多维、混合分布随机变量的系统同样具有很好的不确定抑制能力，可以处理系统存在初始状态不确定的问题.

通过对F-16飞行器的仿真分析可以得知，该方法可以有效应用于飞行控制中的动力学预测以及具有鲁棒特性的控制指令生成.

5 结论

本文提出一种基于混沌多项式的鲁棒优化方法，将混沌多项式方法应用于飞行器控制设计中.本文利用混沌多项式和Galerkin投影法将随机动力学系统转换为高维空间中的等效确定性动力学系统.之后，将随机变量的均值和标准差考虑至优化问题的成本函数中，并根据伪谱法对控制指令进行鲁棒优化.最后，通过仿真验证了本文所提方法可以充分利用系统中不确定参数的信息，生成具有良好鲁棒性能的控制指令.并对存在一维随机变量和多维、混合分布随机变量的系统进行分析.分析结果表明，该方法可以有效应用于飞行控制中的动力学预测，并且生成的控制指令对存在初始条件和参数不确定的系统具有良好的鲁棒性.