星凸形多扩展目标跟踪中的传感器控制方法

陈 辉 ，李国财，韩崇昭，杜金瑞

(1.兰州理工大学电气工程与信息工程学院，甘肃兰州 730050;2.西安交通大学自动化科学与工程学院，陕西西安 710049)

1 引言

复杂的现代作战环境必须配合以各种高精度传感器作为智能感知设备，并借助传感器的管理与优化控制策略去进一步改善信息处理的质量.多目标跟踪(multi-target tracking，MTT)[1-4]中的传感器控制是一个时变联合决策与估计中的非线性控制问题，其核心任务是建立可参考并易于量化的目标函数，通过优化目标函数选定或控制传感器的工作方式及运行参数，最终使得对目标函数的评价(例如多目标跟踪性能)达到最优.但在复杂不确定性环境下，涵盖有目标不确定性和量测不确定性的MTT问题中做随机决策解决传感器控制问题仍面临诸多挑战[5-7].

近十几年来，围绕有限集统计(finite set statistics，FISST)解决MTT问题已经成为一种颇为有效的选择，该方法的最大便利在于避免去处理复杂的不确定性数据关联(data association)问题，实质是将多目标的状态和量测分别建模为随机有限集(random finite set，RFS)，进而在多目标贝叶斯滤波框架下直接根据量测集递推计算多目标的后验概率密度.FISST解决MTT的便利，直接推动了传感器管理技术的发展，尤其是在不区分个体目标，而需要在整体上优化MTT性能的时候，FISST可以发挥其得天独厚的“集合优势”.相应的，近几年来以Ristic和Vo为代表的国内外学者直接在FISST理论框架的推动下，提出了一些颇为有效的MTT中传感器控制优化决策的方案.例如，Ristic等人利用Rényi散度为评价函数，分别基于最优多目标贝叶斯滤波器和SMC-PHD滤波器决策多目标跟踪中的传感器控制方案[8-9].随后Hoang和Vo又借助多伯努利滤波器求解Rényi散度给出相应的传感器控制方法[10].之后陈辉等人以多模型多伯努利滤波器为基础，利用巴氏距离提出机动多目标跟踪中的传感器控制策略[11].此外，Gostar等人基于最小化多目标后验离差提出多目标跟踪中的传感器控制方案[12].

但是，传统的MTT方法中都针对的是“点”目标，即假设每个采样时刻每个目标只对应一个传感器量测，所以多目标跟踪优化的着眼点都集中于目标质心运动状态的估计.近些年，由于电子技术的发展，伴随着许多高精度传感器的应用而生，目标每个时刻将会对应多个传感器量测，目标的量测信息呈现出一定的空间范围，这样的目标称为扩展目标(extended target，ET).对于扩展目标跟踪(extended target tracking，ETT)问题的研究在近几年引起了学者们的广泛关注，该方法最大的优势在于能够估计目标的外围轮廓(形状)，而涵盖有多目标形状估计的多扩展目标跟踪(multiple extended target tracking，METT)[13-15]问题的研究成为其研究的焦点.进一步的，为了提升多目标跟踪性能，目标的跟踪优化不能再像传统只优化目标的质心运动状态，必须联合考虑ET的形状估计信息、传感器量测信息和指挥系统的目标任务综合制定决策控制方案对多目标跟踪进行全面优化.由于不能再遵循传统MTT问题中目标与量测关联指派的唯一性假设，这在很大程度上加剧了METT问题求解的难度，也进一步加剧了METT问题中求解传感器控制问题的难度.而且，有限量测信息下构建ET随机时变的形状观测模型尚存在诸多的不确定性.针对复杂的跟踪环境中规划ET星凸形轮廓的量测源，Baum提出的星凸形随机超曲面模型(random hypersurface model，RHM)[16-17]很好的解决了METT中星凸形不规则形状的建模问题，该方法借助有限阶傅里叶级数展开提取星凸形扩展目标的不规则轮廓形状参数，再结合尺度因子缩放目标轮廓完成不规则形状星凸形扩展目标量测源模型的建模.与此同时，近几年基于FISST已经出现了一些有效的多扩展目标滤波器[18-20]，由于可以将多扩展目标形状信息和运动参数直接利用RFS进行描述，这就为METT传感器控制的研究提供了极大的便利.

综上所述，涵盖有多扩展目标形状估计的METT问题已成为基于现代高精度传感器目标跟踪技术的热点，对带有形状信息在内的状态估计依据传感器控制技术进行最大程度的优化势在必行.本文METT中的传感器控制在部分可观测马尔可夫决策过程(partially observable Markov decision process，POMDP)[21]

的理论框架下进行.而与传统MTT问题跟踪优化的不同在于，METT的跟踪优化需要考虑多目标的质心运动状态和多目标的随机外围轮廓(形状)信息的联合优化.所以，本文的核心内容和贡献在于提出了METT中的传感器控制方法.首先分析给出METT中基于信息论的传感器控制方法.其次，利用RHM和扩展目标的泊松量测模型[22-23]联合对星凸形ET的量测源进行建模，利用容积卡尔曼滤波器(cubature Kalman filter，CKF)[24]求解RHM的非线性伪量测方程，结合势均衡多扩展目标多伯努利(cardinality balanced multiple extended target multi-Bernoulli，ETCBMeMBer)滤波算法，最终给出RHM容积卡尔曼高斯(Gaussian mixture，GM)混合ETCBMeMBer(RHM-CKGM-ETCBMeMBer)滤波器跟踪多扩展目标.进一步的，利用高斯混合密度间的柯西施瓦兹(Cauchy-Schwarz，CS)散度[25]作为传感器控制的评价函数，以信息增益最大化准则决策最优传感器控制方法.另外，本文还以扩展目标势估计的后验期望值(posterior expected mumber of extended targets，PENET)最大化为准则提出相应的传感器控制方法.最后，通过构造不规则形状多扩展目标跟踪优化的仿真实验验证文中所提传感器控制方法的有效性.

2 问题描述

2.1 多扩展目标跟踪中基于信息论的传感器控制方法

本文在POMDP理论框架下，基于信息准则进行METT中传感器控制方法的研究.POMDP理论框架下传感器控制主要包含几个关键要素，其中RFS框架下当前多扩展目标状态信息的不确定性由当前时刻多扩展目标的后验概率密度函数pk(Xk|Z1:k)表示，多扩展目标状态集合可以表示为

m表示目标的个数.基于RHM的扩展目标的状态向量由运动状态参数向量与形状参数向量两部分构成，即k时刻第i个扩展目标的状态向量可以表示为此外，通常利用Uk表示k时刻POMDP包含的可实现的传感器的控制集合，每一个控制方案ν∈Uk决定了传感器下一时刻的位置.而最为关键的要素是每个传感器控制方案ν都需要建立传感器控制优化的评价函数R(ν).文中以多扩展目标先验概率密度与后验概率密度之间的信息散度作为多扩展目标跟踪优化的评价准则，进而决策出最优的传感器控制方案uk.

首先，表示传感器控制质量的评价函数为

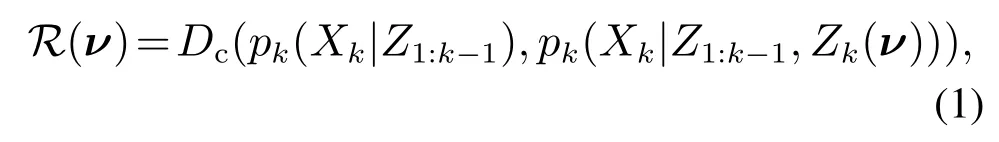
其中:pk(Xk|Z1:k-1)，pk(Xk|Z1:k-1，Zk(ν))分别表示多扩展目标状态的先验与后验概率密度函数，Zk(ν)表示包含控制方案ν的多扩展目标的预测理想量测集(predicted ideal measurement set，PIMS)，并且PIMS构建需要结合具体扩展目标的量测源模型.然后，构造目标函数去求解最优的传感器控制方案uk，即

2.2 星凸形随机超曲面模型的描述

Baum提出的星凸形随机超曲面模型是星凸形扩展目标的量测源模型，可以描述星凸形扩展目标的量测源随机位置.该模型假设每个量测源是目标形状边界随机缩放之后产生的随机超曲面上的一个元素，因此星凸形RHM是一种量测集为超曲面的随机集模型.下面将详细分析给出利用星凸形RHM对本文研究对象星凸形ET的量测源建模过程.

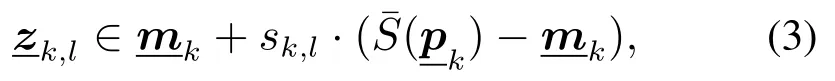
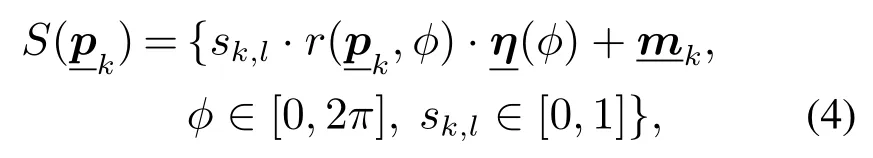
其中形状参数向量为

该形状参数向量为目标状态向量的重要组成部分，并为文中所提传感器控制方法在形状方面的优化提供的了依据.

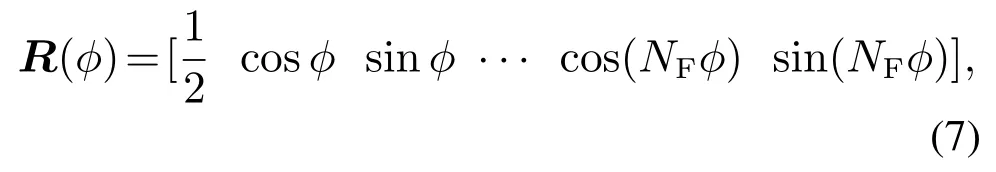
即径向函数可以表示为

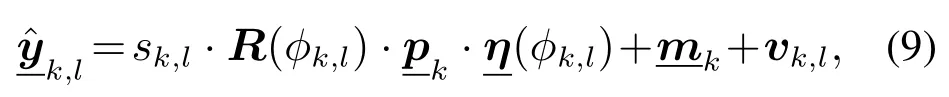
其中:φk，l是未知的，通常用k时刻目标质心位置的点估计值和量测之间的向量与x轴的夹角近似代替.进一步，式(9)可推导为如下伪量测方程:

利用式(10)不仅可以描述星凸形RHM的观测模型，还可以利用它建立传感器控制的PIMS，为多扩展目标的跟踪优化决策提供了基础.

3 基于RHM的多扩展目标跟踪算法

基于RHM的容积卡尔曼GM势均衡多扩展目标多伯努利跟踪算法，其主要由预测步和更新步两部分组成，具体的实现过程如下所示:

1) 预测步.

ET和点目标所对应的量测数目不同，因此RHMCKGM-ETCBMeMBer算法和点目标CBMeMBer具有相同的预测步，即如果k-1时刻的多扩展目标后验概率密度为多伯努利密度

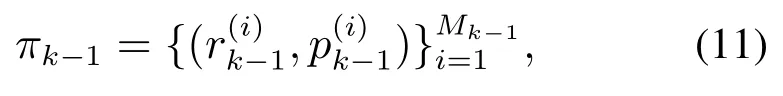
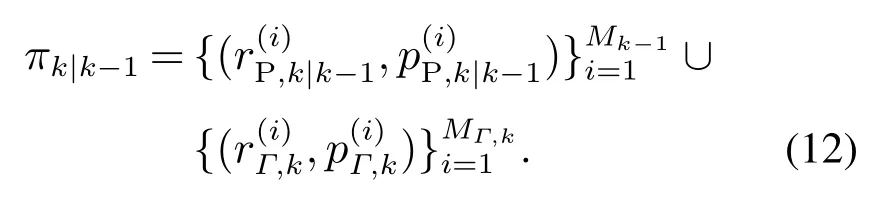
可以看出式(12)由两部分组成，其中:后一项表示k时刻新生目标的多伯努利参数，前一项为存活目标的多伯努利参数，并且概率密度函数可用高斯混合加权和的形式近似表示为

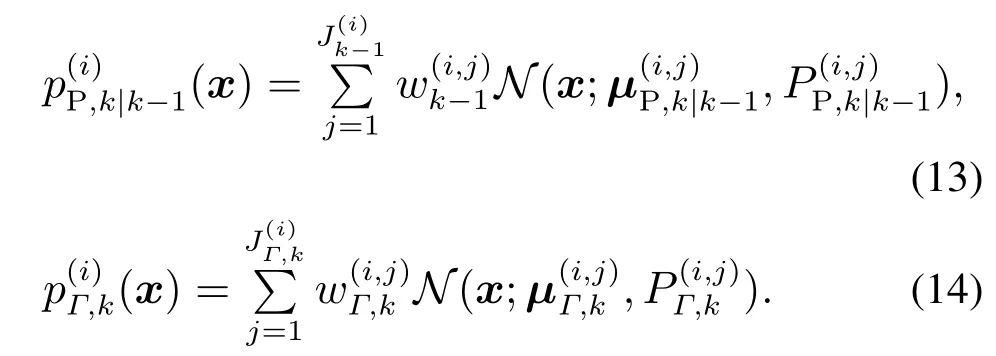
式(13)-(14)中:w(i，j)表示近似第i个伯努利RFS概率密度函数的第j个高斯分量的权值，μ(i，j)表示该分量的均值，P(i，j)为协方差矩阵.

2) 更新步.

如果每个ET每一时刻所产生的量测数目服从均值为γ的泊松分布，则结合文献[23]提出的泊松似然模型就可以实现对多扩展目标概率密度函数的递推更新.然而，泊松似然模型应用于目标的一簇量测，因此在更新多扩展目标概率密度之前必须对量测集进行划分，文中采用距离划分(distance partitioning，DP)方法[26]进行量测集的划分.下面将给出多扩展目标概率密度的量测更新过程.

量测更新部分为

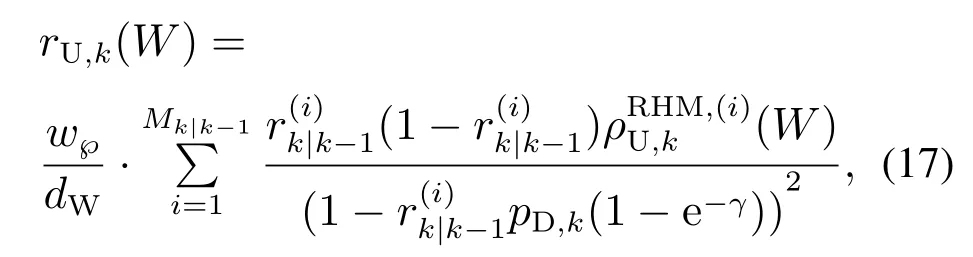
式中:w℘为每种量测集划分℘的权值，dW为每个划分单元的权值，并且

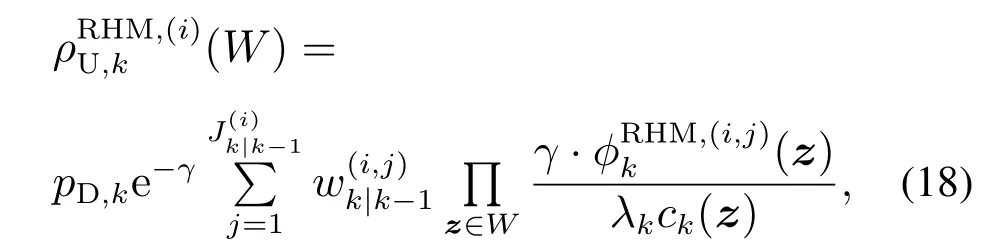
式(18)中:λk为k 的杂波平均数，ck(z)为概率密度，为基于RHM的单个量测的似然函数.由文献[23]可知，如果每个扩展目标在采样周期内的量测数目服从均值为γ的泊松分布，那么(单)扩展目标的泊松似然函数为

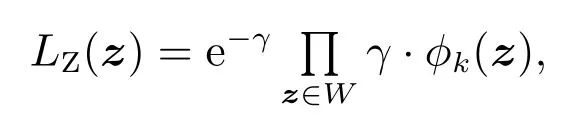
其中φk(z)为量测所对应的似然.进一步由文献[20]多扩展目标多伯努利滤波器的高斯混合实现可知，式(18)是泊松似然模型在扩展目标跟踪应用的体现.此外，概率密度函数可表示为

高斯混合中每个高斯分量对应的权值为

首先，计算基本容积点ξi和对应的权值wi，并依据ξi和k时刻每个高斯分量的预测均值以及协方差获取容积点其中:

由三阶容积原则可知nc表示容积点总数，且nc与状态维数nx的关系为nc=2nx.其中，可通过对nx维单位向量e=[1 0··· 0]T的元素进行全排列和改变元素符号的方式得到式(21)中的完全对称点集[1]，[1]i表示[1]中的第i个点.进一步，结合基本容积点ξi并通过下式计算容积点

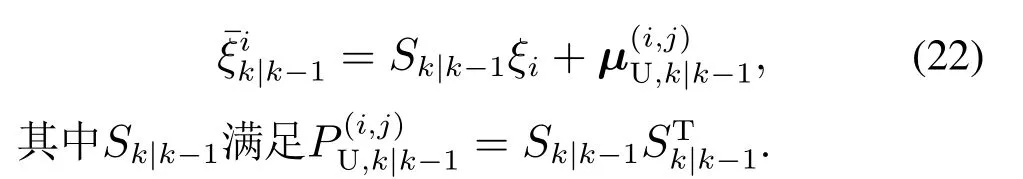
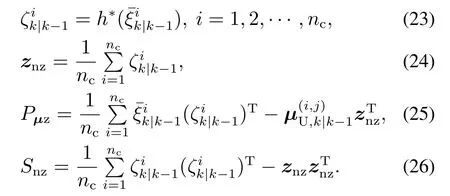
最后，可得增益矩阵Kk=Pµz(Snz)-1，进一步结合伪量测0更新每个高斯分量的均值和协方差并计算似然函数

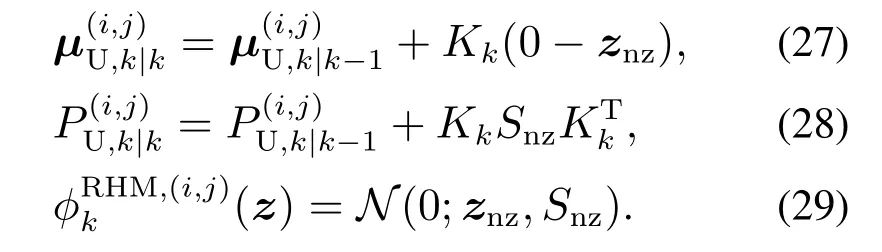
进而，更新计算式(17)-(20)的相关参数.

4 多扩展目标跟踪中传感器控制方法

本节主要基于RHM 多扩展目标跟踪算法研究METT 中的传感器控制方法.由于而高斯混合分布间的CS散度明确存在闭式解[25]，这对基于高斯混合实现的多扩展目标滤波器的传感器控制带来了方法求解上的便利.首先，文中详细给出基于CS散度的传感器控制方法.然后推导GM-PENET的实现方式并给出基于该准则的传感器控制方法.最后，详细给出METT中上述两种传感器控制方法的实现伪码.

4.1 基于柯西施瓦兹散度的多扩展目标跟踪传感器控制方法

假设p0和p1分别表示多扩展目标先验和后验两个概率密度函数，则它们之间的CS散度可表示为

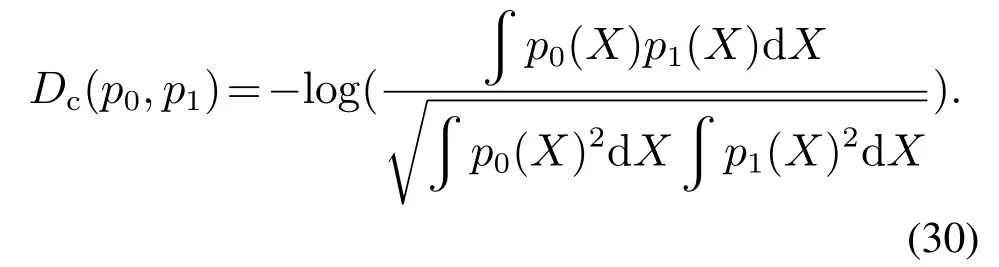
根据式(1)(30)，扩展目标跟踪中传感器控制的CS评价函数为

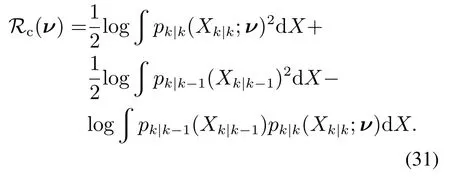
在RHM-CKGM-ETCBMeMBer中，利用多个伯努利过程去近似多扩展目标的概率密度函数，在此基础上利用一组加权的高斯分量近似了每个伯努利过程的概率密度函数.因此由式(31)可知，扩展目标跟踪中传感器控制CS散度的求解主要是两个GM之间的计算.其具体的求解过程如下:

首先，由式(11)-(14)并结合扩展目标的存活概率pS，k可得预测多扩展目标概率密度函数，其中:

然后，确定传感器控制集合Uk中每种控制方案ν的传感器位置xs，k(ν).随后对于每一种控制方案去产生唯一的一组PIMS，即

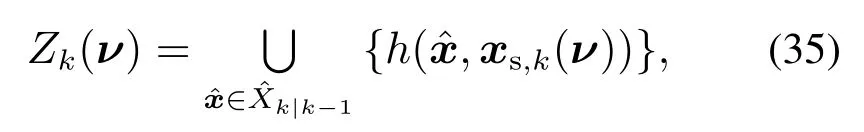
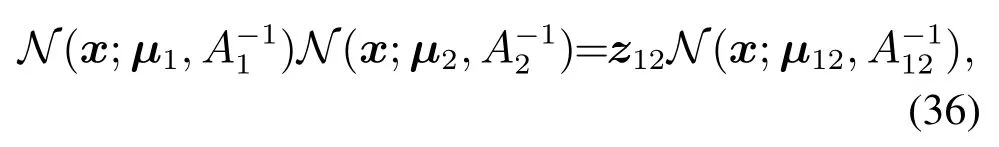
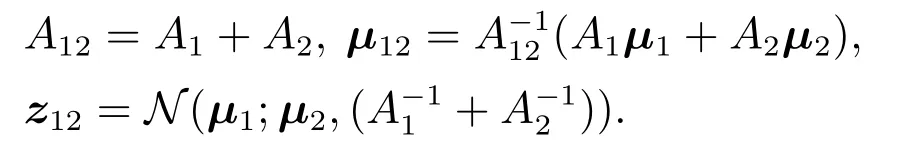
参照文献[27]中的推导方式，借助式(36)可将式(31)推导为

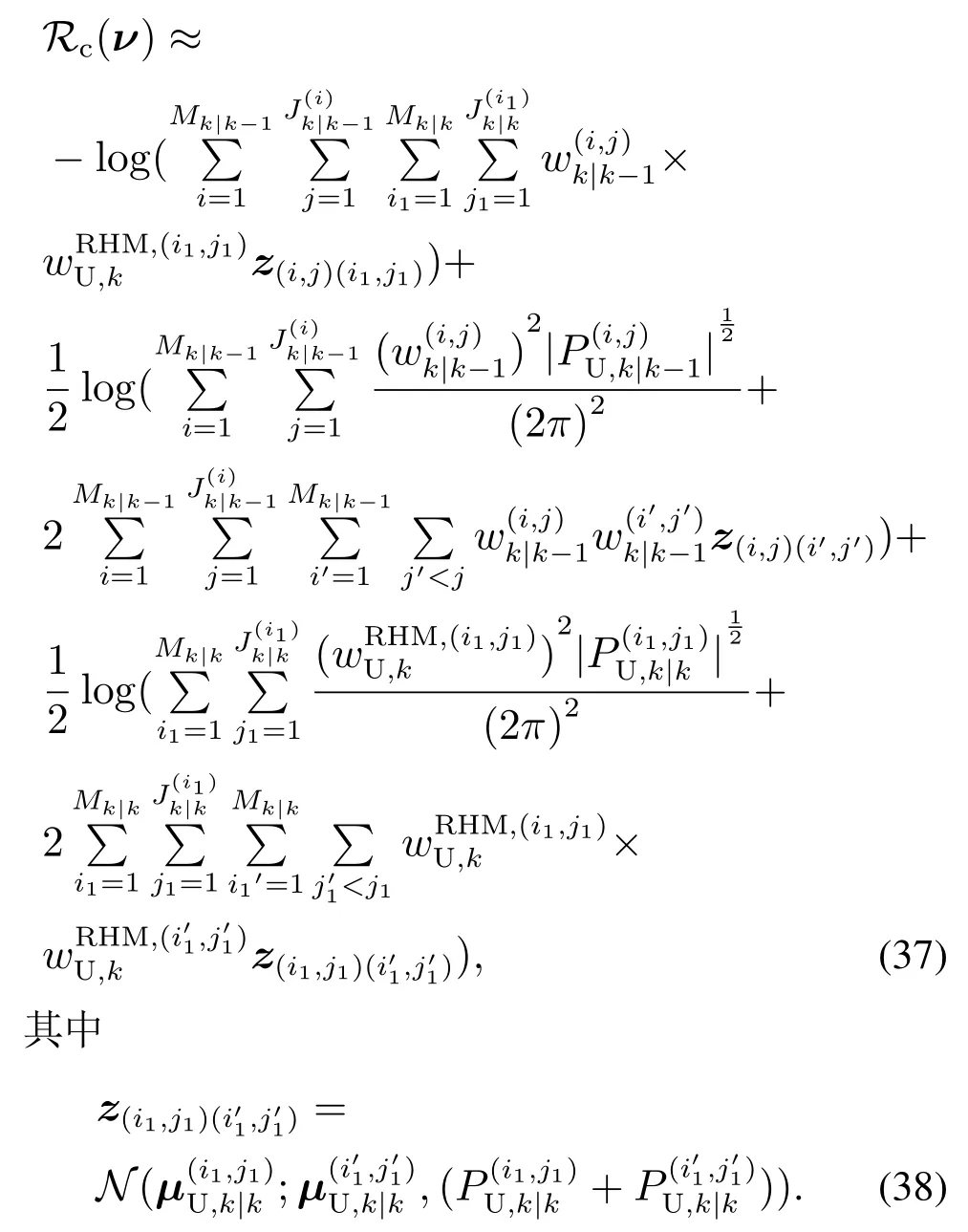
z(i，j)(i1，j1)，z(i，j)(i′，j′)的计算也类似.与点目标CS不同的是，扩展目标的CS散度中每个高斯分布的均值和协方差都包含了目标的形状信息，这就为扩展目标传感器控制在形状方面的优化提供了依据.

4.2 基于PENET准则的多扩展目标跟踪传感器控制方法

基于PENET准则的传感器控制是从控制集合Uk中决策出相应的控制方案，使得跟踪系统对扩展目标势估计的后验期望值(PENET)达到最大.文献[28]给出了点目标跟踪中PENT准则的表达式，即对每种控制方案ν∈Uk，

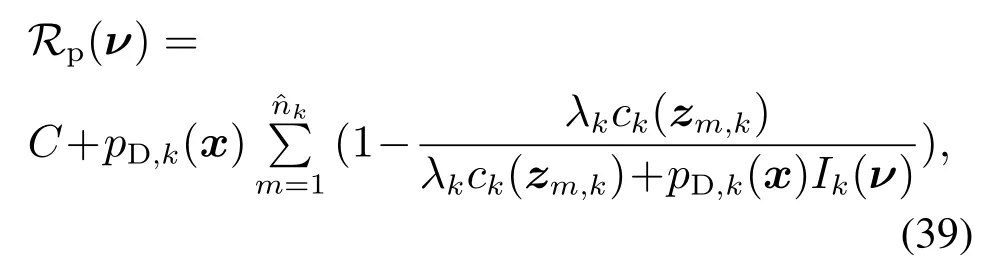
其中:C为独立于控制方案ν的常数，为量测个数，zm，k属于理想量测集Zk(ν).结合式(39)给出的PENT准则计算公式，可推导出扩展目标中PENT准则的表达式，即PENET为

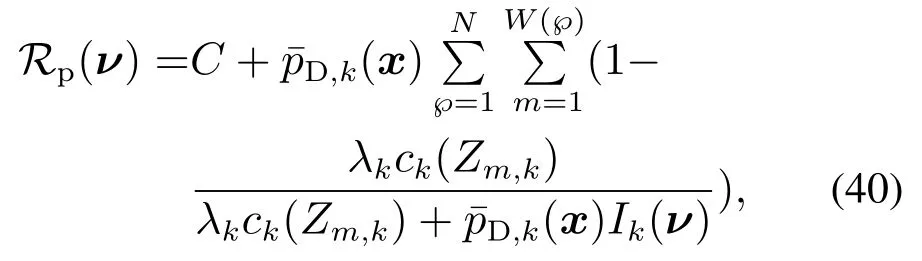
其中:N表示量测集划分的个数，W(℘)表示每种划分℘所对应的量测簇的个数.基于GM-CBMeMBer中对PENT准则的求解思路，本文将结合RHM-CKGMETCBMeMBer，推导PENET准则的详细求解过程.其中

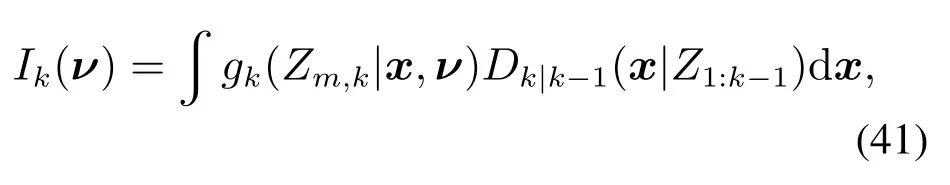
在RHM-CKGM-ETCBMeMBer的实现过程中，强度函数为

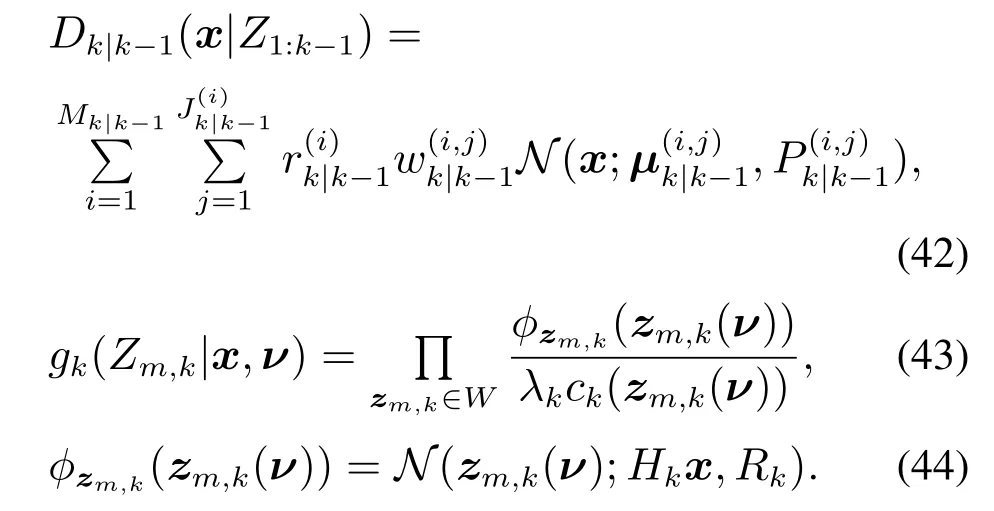
基于式(42)-(44)，下面将详细推导给出式(41)的具体求解过程:首先，将式(44)代入式(43)中可将式(43)表示为

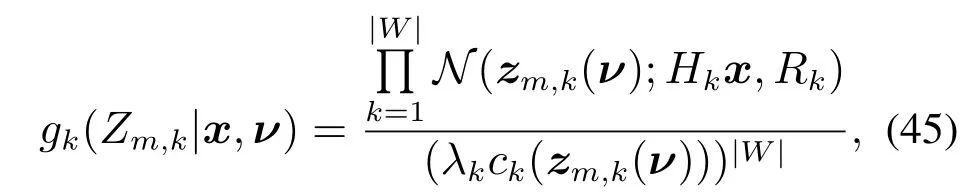
然后，结合式(36)对式(45)进行化简，可将式(45)化简为

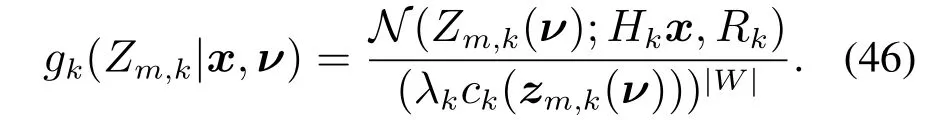
最后，将式(46)(42)代入式(41)中，并再次利用高斯乘积公式可得

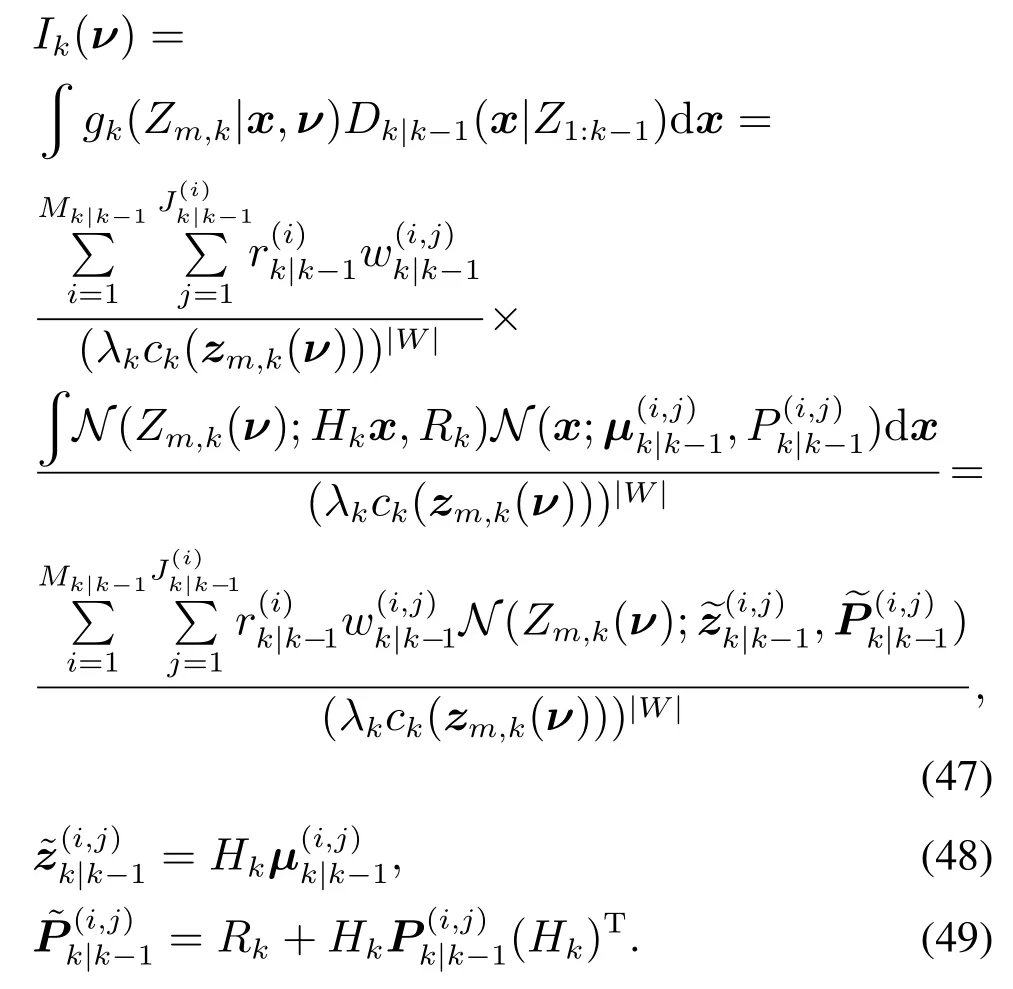
由RHM-CKGM-ETCBMeMBer的实现过程可以得到式(48)-(49)中高斯分布的均值和协方差.

4.3 算法程序的伪码

为了更详尽的说明算法流程，下面给出本文算法的伪码.

步骤2传感器控制.

a) 基于CS散度的传感器控制.

对传感器控制集合Uk中的每种控制方案ν∈Uk确定传感器位置xs，k(ν).

依据每种控制方案的传感器位置xs，k(ν)和式(35)产生相应的理想量测集合Zk(ν).

对每种控制方案的Zk(ν)进行量测集划分，然后根据式(15)-(29)进行伪更新.

通过式(37)计算每种控制方案所对应的GM条件下评价函数(CS散度)的闭式解Rc(ν).

求取max(Rc(ν))，并确定最终控制方案uk.

传感器在新控制位置xs，k(uk)产生实际量测Zk(uk).

b) 基于PENET准则的传感器控制.

对传感器控制集合Uk中的每种控制方案ν∈Uk确定传感器位置xs，k(ν).

依据每种控制方案的传感器位置xs，k(ν)和式(35)产生相应的理想量测集合Zk(ν).

对每种控制方案的Zk(ν)进行量测集划分，然后根据式(15)-(29)进行伪更新.

计算式(41)-(49)给出PENET准则高斯混合实现形式的相关参数.

按式(40)计算Rp(ν)，并确定最终控制方案uk.

传感器在新控制位置xs，k(uk)接收实际量测Zk(uk).

步骤3更新.

5 仿真实验

5.1 传感器控制集合与仿真场景

首先，如果已知k时刻传感器最优控制方案所决定的传感器的位置xs，k=[xs，kys，k]T，那么k+1时刻传感器的控制集合Uk+1为

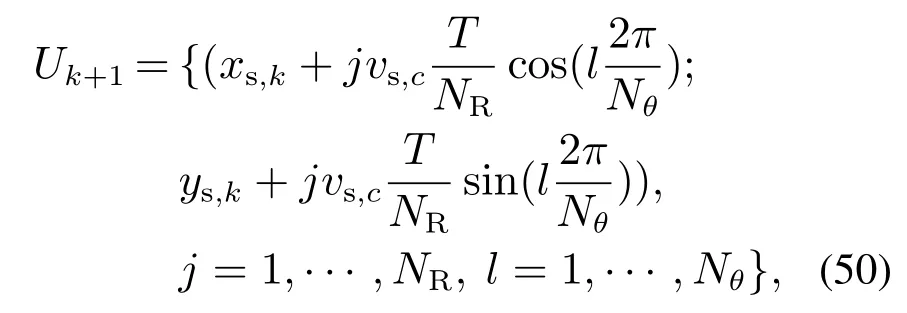
其中设定NR=2，Nθ=8，则控制集合Uk+1总共有17种控制方案(包含传感器静止不动).设定传感器的初始位置为原点，传感器容许的控制速度vs，c=5 m/s.

然后，构造做匀速直线运动的3个星凸型不规则形状扩展目标进行跟踪仿真实验，k时刻每个扩展目标的状态演化模型为

其中:状态转移矩阵Fk=过程噪声协方差Qk=表示nf阶的单位矩阵，nf为有限阶傅里叶级数的阶数，文中取nf=分别为

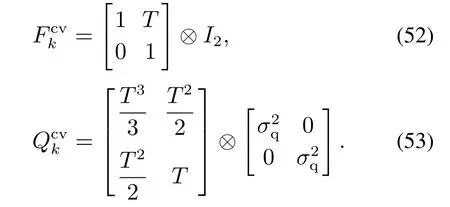
式(53)中采样周期T=1 s，总共采样50个时刻，过程噪声标准差σq=0.01 m/s2.其他仿真参数分别取值为:传感器的检测概率pD，k与目标的存活概率pS，k均为0.99.杂波个数服从均值为10的泊松分布，且在观测区域内([-500，500]m×[-500，500]m)均匀分布，量测数据直接构建在笛卡尔坐标系下，杂波密度为1×10-5m-2.另外，量测噪声协方差为

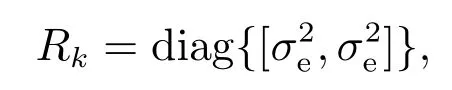
标准差σe=0.1，尺度因子仿真建立泊松似然模型，每个扩展目标单个周期内的量测数目服从均值γ=20的泊松分布，并且设定目标航迹删除的阈值Tr和高斯分量的截断阈值Tw分别为10-3和10-4，高斯分量的最大数Jmax=100，伯努利过程的阈值rm=0.5.

此外，初始时刻新生目标被建模为多伯努利RFS的形式，即有其中存在概率为0.03，每个伯努利随机有限集的初始概率密度为

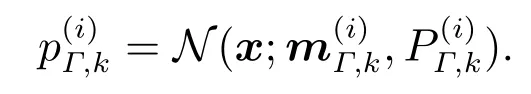
定义扩展目标初始形状是半径为3 m的圆，则

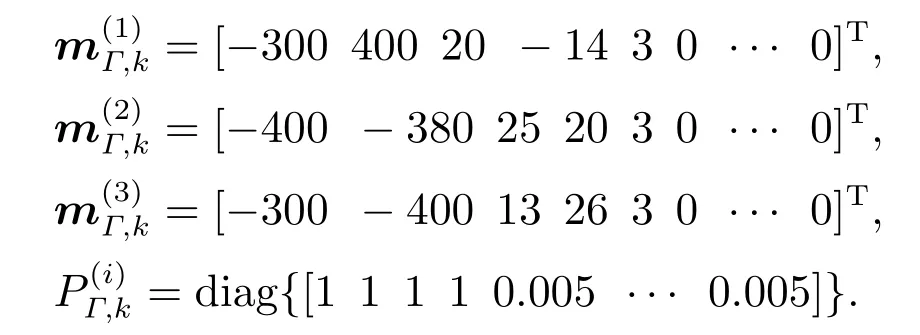
每个扩展目标的新生、消亡时刻、初始位置及真实形状如表1所示.

表1 目标的初始参数及真实形状Table 1 Initial parameter and true shape of target

5.2 仿真分析

首先，图1给出每个扩展目标的真实运动轨迹.然后，利用RHM-CKGM-ETCBMeMBer跟踪设定场景中多个不规则形状的扩展目标.构造5种传感器控制方案对比验证文中所提控制方法对多扩展目标跟踪优化的有效性.其中:方案1是“Stationary”，表示传感器是静止状态;方案2是“CS control”，即文中所提出的基于Cauchy-Schwarz散度的多扩展目标跟踪传感器控制方法;方案3是“Random control”，即每一个时刻从可实现的传感器控制集合Uk+1中随机选取控制方案;方案4是“Prior-control”，即先验设定经典的所谓Zigzag传感器控制方案，其传感器轨迹如图2所示;方案5是“GM-PENET”，即文中所提“PENET”传感器控制方法，旨在最大化多扩展目标势估计的精度.

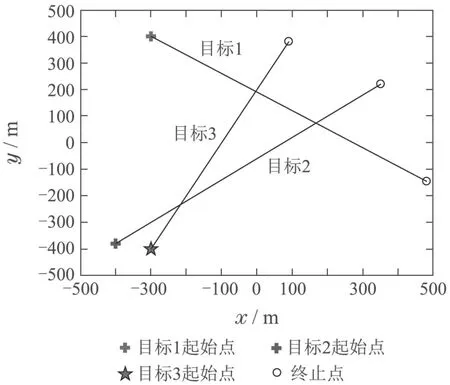
图1 目标的真实轨迹Fig.1 Actual target trajectories

图3是5种控制方案对多扩展目标的整体跟踪效果图，由于文中实验方案比较多，导致整体跟踪效果图重合，但可以清晰可见上述5种传感器控制方案与RHM-CKGM-ETCBMeMBer的结合都能实现对不规则形状多扩展目标的有效跟踪.

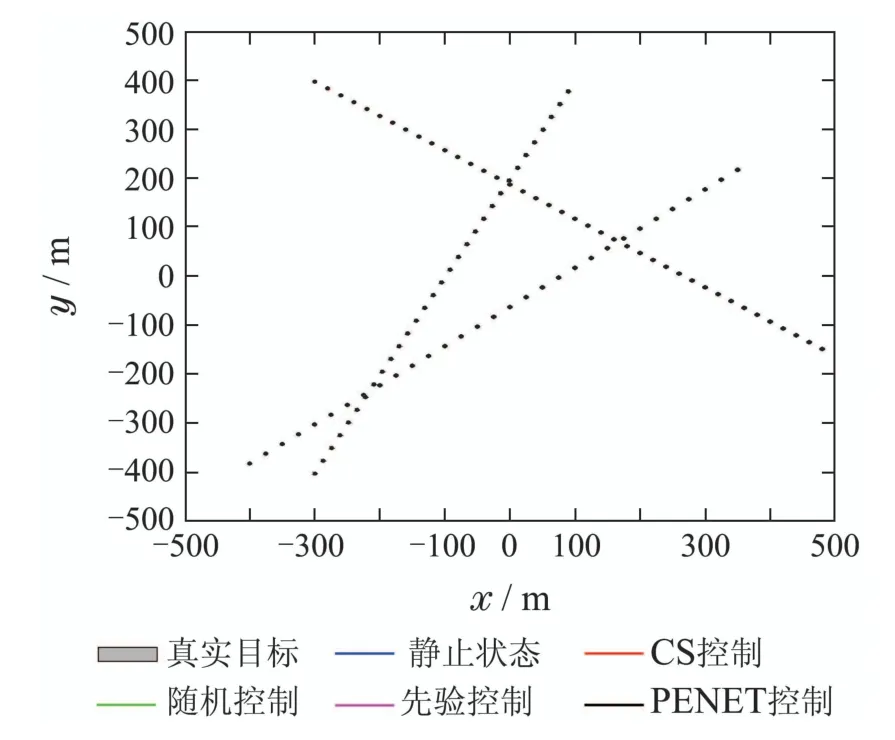
图3 5种控制策略整体跟踪效果图Fig.3 The tracking result of five control strategies

图4-6分别给出单次仿真实验下，在多扩展目标接近消亡时刻，5种传感器控制方案对扩展目标形状的跟踪效果图以及形状估计局部放大图.可以得到，随着量测信息的不断累积，基于所有控制方案的目标跟踪算法都基本能实现对多扩展目标的跟踪估计.进一步的，由形状估计的局部放大图可知，方案1对应估计效果最差.这是因为在多扩展目标跟踪的过程中，并没有介入传感器控制的优化过程.方案3和方案4有明确的传感器控制动作，他们在多(点)目标的跟踪优化的有效性已得到验证[9]，而在本论文的实验中，进一步验证了他们对于多扩展目标跟踪中的形状估计也有相对不错的优化效果.仔细甄别多扩展目标形状估计的放大特征，文中所提的方案2与方案5对多扩展目标形状轮廓细节的估计上更为精确，这主要是因为基于预知的PIMS和递推的多扩展目标密度，决策了相对最优的多扩展目标量测过程，从而提高了多扩展目标形状跟踪的性能.

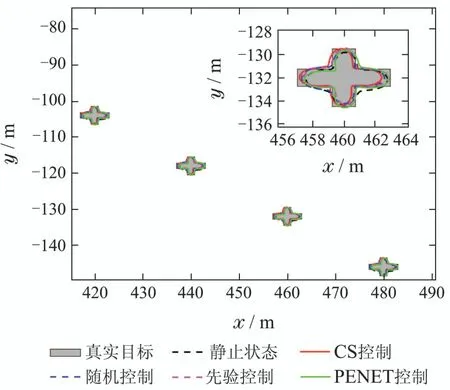
图4 目标1的形状跟踪局部放大图Fig.4 The partial enlarged effect of shape estimation for Target 1

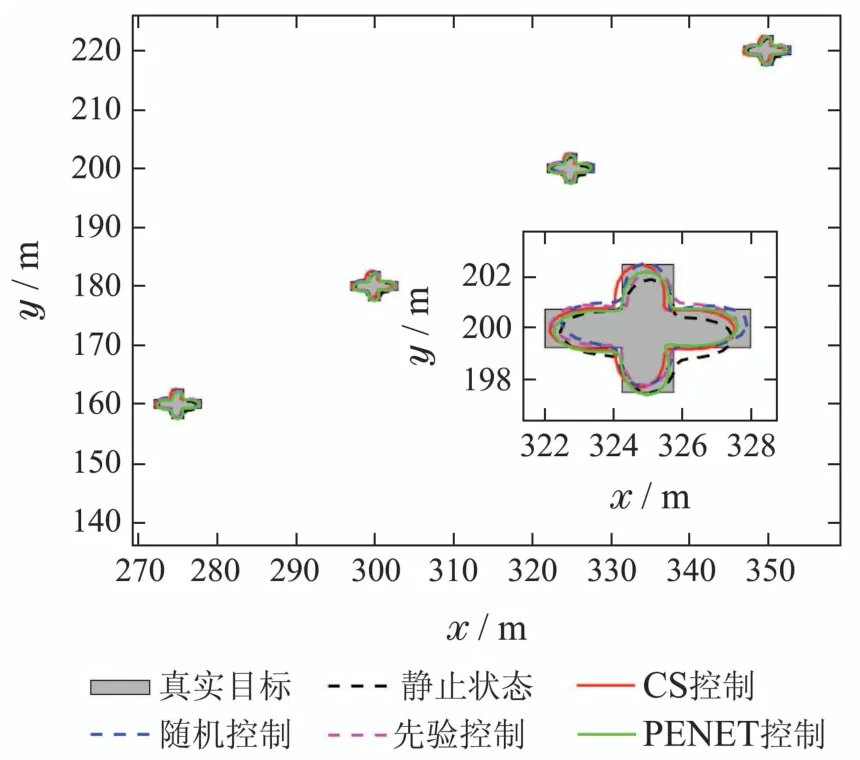
图5 目标2的形状跟踪局部放大图Fig.5 The partial enlarged effect of shape estimation for Target 2

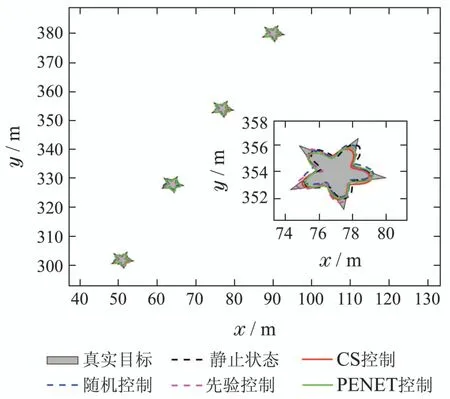
图6 目标3的形状跟踪局部放大图Fig.6 The partial enlarged effect of shape estimation for Target 3

图7-8分别给出与上述仿真对应的方案2与方案5的传感器控制轨迹.由控制轨迹可以看出，在整个跟踪过程中，传感器会始终依据最优评价准则不断地调节自身的位置，使得在当前时刻传感器处于对所有扩展目标的最佳观测位置.

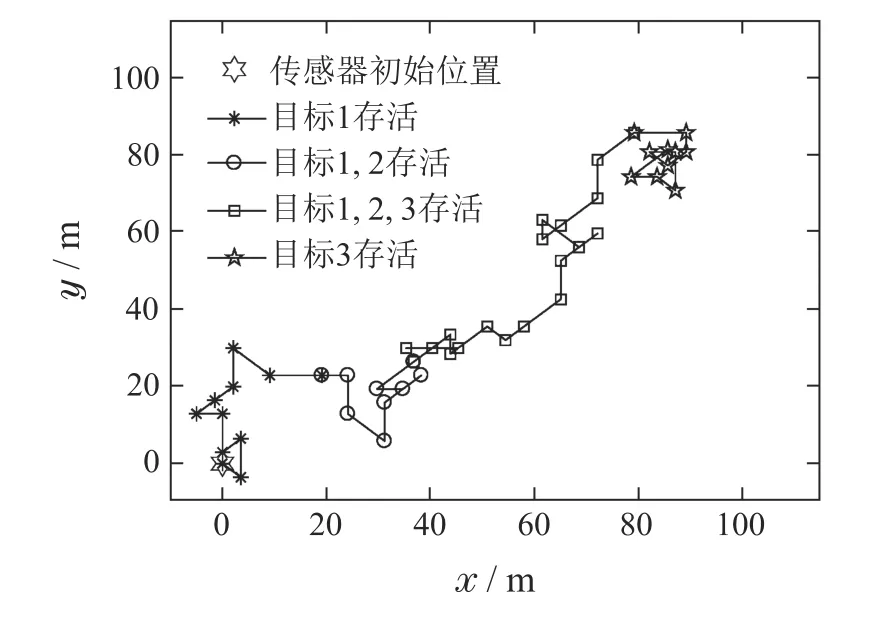
图7 单次MC方案2的传感器控制轨迹Fig.7 Sensor control trajectory in the second control strategy

图8 单次MC方案5的传感器控制轨迹Fig.8 Sensor control trajectory in the fifth control strategy

本文利用最优子模式分配(optimal subpattern assignment，OSPA)距离[29]去评价多扩展目标的质心位置估计.由OSPA 的定义可知若集合X=的元素个数m小于集合Y=的元素个数n，则这两个集合之间的OSPA距离为

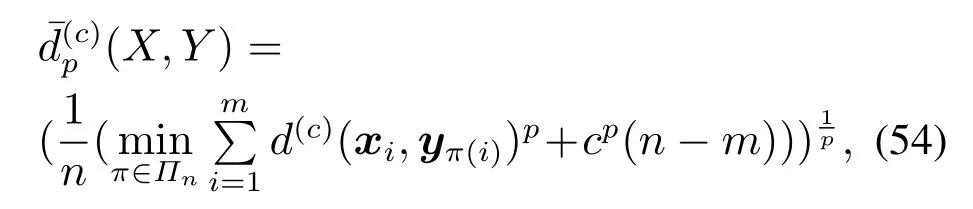
其中:文中设定能调节集合元素数误差的截断系数c=1.5，距离阶次p=1;式(54)中

Πk表示集合{1，2，···，k}的全排列，π(i)表示该全排列的第i种排列，当m＞n时，

由图9所示的100次蒙特卡罗(Monte Carlo，MC)仿真实验所得的5种传感器控制方案OSPA距离的统计值可知，每种传感器控制方案下，多扩展目标质心位置估计的OSPA距离值都非常小，这是因为每个扩展目标都对应了多个量测源，多源信息融合下会显著提升目标质心状态估计的性能，而且传感器控制会进一步优化目标跟踪的质量.为了能够区分不同控制方案之间的差别，对OSPA进行均值统计(如表2所示)发现，相比较其他方案，方案2和方案5的控制优化效果较好一些，从而验证了所提控制优化算法的性能.

表2 质心位置估计OSPA均值Table 2 OSPA average of centroid position estimation

图10给出了100次MC仿真实验验证下，5种传感器控制方案所对应的多扩展目标跟踪算法对多个扩展目标数目(势)估计的统计值.图10可知，5种传感器控制方案都能对多扩展目标数目进行准确估计，但是由表3所统计的MC实验中多扩展目标势估计的误差均值可得，方案5基于“GM-PENET”的传感器控制方案对目标数目的估计要优于其他控制方案，这验证了GM-PENET是以扩展目标势为优化目的的传感器控制方案.

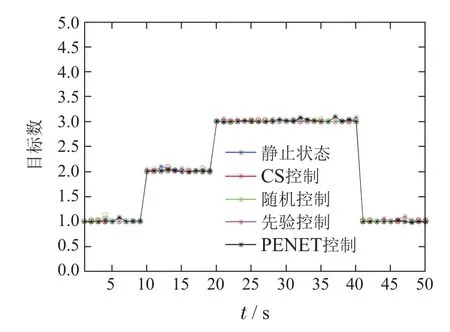
图10 5种传感器控制方案的势估计统计Fig.10 Cardinality estimation statistics of five control strategies

表3 5种方案势估计误差均值Table 3 Cardinality estimation error average

表4统计了MC仿真实验中5种传感器控制算法执行效率的对比.由表4可知，方案1、方案3和方案4对应计算复杂度最小，因为它们基本都没有传感器控制的决策计算过程参与其中.显然，方案2与方案5对应计算复杂度较高，通过分析，额外增加的计算复杂度花费在了相应的传感器控制方案的决策计算上，花费的计算代价换回了更高的估计精度(运动参数和形状参数)，即以时间效率为代价换取扩展目标估计精度的提升.所以，针对传感器控制算法的进一步优化和算法执行效率的不断提升也需要在今后的工作中不断研究.另外，文中利用形状估计的局部放大显示估计的效果，但在形状估计的性能评价上也需要做进一步的研究.

表4 5种控制算法执行效率对比Table 4 Comparison of execution efficiency of five control algorithms

6 结论

本文提出了多扩展目标跟踪中传感器控制的优化策略.首先利用RHM对多扩展目标的不规则形状进行建模，然后基于RHM-CKGM-ETCBMeMBer多扩展目标跟踪算法结合CS散度，基于信息增益最大化为目的进行多扩展目标跟踪中传感器控制方法的研究.此外，本文还详细推导了GM-PENET的具体求解过程，该控制方案以多扩展目标势估计的后验期望最大化为优化目标.最后，依据文中所提的传感器控制方案对多个不规则形状的扩展目标进行跟踪估计，仿真结果验证了文中所提传感器控制方案在多扩展目标跟踪定位、形状估计和势估计上的优化效果.