对2020年高考山东卷第21题的探究

山东省莒南县第一中学(276600) 李 明

今年是山东高考不分文理科第一年.高考结束后,笔者针对导数解答题对部分考生做了调查,结果显示:大部分考生都能完成第一问的解答;而对于第二问,由于无法直接分离参数,部分考生利用分类讨论,但对如何分类,分类的依据是什么不清楚,导致解答步骤不完整.以下笔者就该题探究如下.

题目(2020年高考山东卷第21 题)已知函数f(x)=aex-1-lnx+lna.

(1)当a= e 时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;

(2)若f(x)≥1,求a的取值范围.

本题主要考查导数几何意义、利用导数研究不等式恒成立问题,考查综合分析求解能力,分类讨论思想和等价转化思想,属较难试题.

解析(1)三角形面积为(过程略).以下考虑问题(2)的解答.

思路一(直接分类讨论.标准解答)当0＜a ＜1 时,f(1)=a+ lna ＜1.当a= 1 时,f(x)= ex-1-lnx,f′(x)= ex-1-当x ∈(0,1)时,f′(x)＜0; 当x ∈(1,+∞)时,f′(x)＞0, 所以当x= 1 时,f(x)取得最小值, 最小值为f(1)= 1, 从而f(x)≥1.当a ＞1 时,f(x)=aex-1-lnx+lna≥ex-1-lnx≥1.综上,a的取值范围是[1,+∞).

评注此种解法简洁,但考生不易想到分类的依据,并且当a ＞1 时的放缩也对考生提出了较高的要求.

思路二( 必要性探路+ 隐零点)依题意, 对任意x ∈(0,+∞),aex-1-lnx+ lna≥1, 则f(1)≥1, 即a+lna≥1,令g(a)=a+lna,则g(a)单调递增,g(1)=1,故上述不等式等价于g(a)≥g(1),所以a≥1.

f′(x)=aex-1-,f′(x)在(0,+∞)上单调递增,又因为f′(1)=a-1 ≥0,取b=则f′(b)＜0,根据零点存在性定理, 存在唯一的零点x0∈(b,1], 使得f′(x0)= 0, 即故当x ∈(b,x0),f′(x)＜0,f(x)单调递减;当x ∈(x0,+∞),f′(x)＞0,f(x)单调递增.f(x)min=f(x0)=aex0-1-lnx0+lna=-lnx0+lna只需保证f(x0)大于等于1 即可,显然f(x0)在x0∈(b,1]上单调递减,f(x0)≥f(1)=1+lna,又a≥1,则1+lna≥1,f(x0)≥1,即f(x)≥1,当且仅当a= 1,x= 1 时等号成立,故a的取值范围是[1,+∞).

评注利用条件的必要性, 缩小参数的范围是导数解答题中求参数范围常用手段, 上述解法中先在定义域中取x=1,求出a的一个范围,再在此范围中确定a的取值范围,利用隐零点整体代换,消去指数式,使f(x0)变为一个关于x0的单调递减函数,从而求得a的取值范围.

思路三(隐零点+基本不等式)f(x)=aex-1-lnx+lna,f′(x)=aex-1-, 且a ＞0.设g(x)=f′(x), 则g′(x)=aex-1+＞0,g(x)在(0,+∞)上单调递增,即f′(x)在(0,+∞)上单调递增, 由思路二必要性探路得到a≥1, 下面分类讨论:当a= 1 时,f′(1)= 0, 所以f(x)min=f(1)= 1,f(x)≥1 成立.当a ＞1 时,＜1,＜1, 从而(a-1)＜0, 所以存在唯一x0＞0,使得f′(x0)=aex0-1-= 0,且当x ∈(0,x0)时f′(x)＜0,当x ∈(x0,+∞)时f′(x)＞0.所以aex0-1=即lna+x0-1=-lnx0,因此

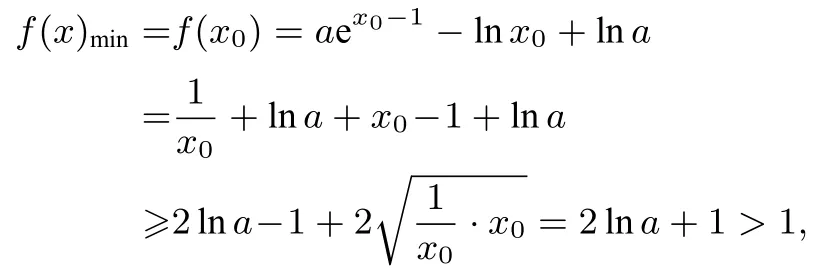
所以f(x)≥1 恒成立.综上所述, 实数a的取值范围是[1,+∞).

评注上述方法还是利用隐零点整体代换,只不过与思路二不同的地方是将指数和对数同时代换,代换之后恰好可以利用基本不等式求最小值,这需要考生熟练掌握隐零点代换及指对互化.

思路四(转换主元+切线放缩)记g(a)=aex-1-lnx+lna(a ＞0),g′(a)= ex-1+＞0,g(a)在(0,+∞)为单调递增函数,由思路二必要性知a≥1.下面分类讨论:当a=1时,g(1)=f(x)= ex-1-lnx,利用切线放缩[1],ex≥x+1,用x-1 替换x,得到

又因为

①+ ②得到ex-1-lnx≥1,即f(x)≥1 恒成立.当a ＞1时,利用单调性得到g(a)＞g(1)≥1,符合题意.综上所述a≥1.

评注在解答多元问题时,如果把它们不分主次来研究,问题很难解决, 这时可视某一个变元作为研究的主要对象,视为“主元”,其他变元暂时视为参数,这种用主元去分析,研究,解决问题的方法叫主元法.本题中a为参数,将a视为主元,g(a)为单调递增函数,只需g(a)≥g(1)= 1 即可,此解法简单自然.

思路五(构造同构式g(x)= ex+x)f(x)=aex-1-lnx+lna= elnaex-1-lnx+lna= elna+x-1-lnx+lna,则

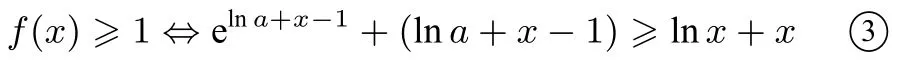
令g(x)=ex+x,则g(lna+x-1)=elna+x-1+(lna+x-1),g(lnx)= lnx+x, 由于g(x)在(0,+∞)上单调递增, 所以③式等价于g(lna+x-1)≥g(lnx)⇔lna+x-1 ≥lnx,即lna+x-1-lnx≥0, 令h(x)= lna+x-1-lnx,只需h(x)min≥0 即可, 因为h′(x)=所以h(x)在(0,1)上单调递减, 在(1,+∞)上单调递增,h(x)min=h(1)=lna≥0,a≥1.

评注对要证明的不等式进行代数变形后,不等式的两侧呈现同构特征,转化为证明g(lna+x-1)≥g(lnx),利用函数单调性找到联系,进而求得a的取值范围.

思路六( 构造同构式g(x)=xex)由于f(x)≥1, 即aex-1-lnx+lna≥1(a ＞0,x ＞0),所以aex-1≥,故

令g(x)=xex,则④式等价于

又g′(x)= ex(x+ 1), 所以g(x)在(0,+∞)上单调递增,由⑤可知总有x≥则a≥令h(x)=当x ∈(0,1)时,h′(x)＞0, 此时h(x)单调递增,当x ∈(1,+∞)时,h′(x)＜0,此时h(x)单调递减,从而h(x)max=h(1)=1,所以a的取值范围是[1,+∞).

评注构造与思路五不同的同构式,有利于拓展学生思维.

思路七(反函数法)性质[2]:若F(x)≥G(x)恒成立,且G(x)=F-1(x),则F(x)≥G(x)⇔F(x)≥x≥G(x).

在本题中,f(x)≥1⇔aex-1≥lnx -lna+ 1, 令g(x)=aex-1, 则g-1(x)=+ 1 = lnx -lna+ 1.f(x)≥1⇔g(x)≥g-1(x), 根据性质只需g(x)≥x即可,即aex-1≥x,a≥令h(x)=(x ＞0),只需a≥h(x)max.h′(x)=故h(x)在(0,1)上单调递增,在(1,+∞)上单调递减.所以h(x)max=h(1)= 1,a的取值范围为[1,+∞).

评注对不等式进行代数变形后,发现不等式两侧互为反函数,利用反函数性质使得问题变得简单.

思路八(函数凹凸性+导数几何意义)

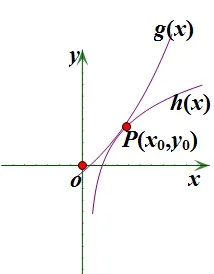
图1

图2

f(x)≥ 1⇔ aex-1+ lna≥ lnx+ 1.记g(x)=aex-1+lna,h(x)= lnx+1,因为g(x)是凸函数,h(x)是凹函数如图1 所示,设曲线g(x)与h(x)相切于点P(x0,y0),则

令t(x0)= 2 lnx0-+x0, 显然t(1)= 0, 且t′(x0)=+1 =＞0,所以t(x0)在(0,+∞)单调递增,t(x0)= 0 的根为x0= 1.如图2,只要g(x0)≥h(x0)便是a的取值范围.故

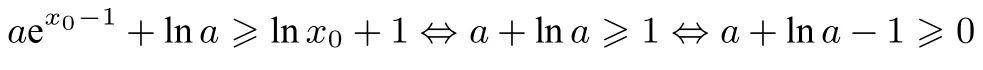
令m(a)=a+lna-1,m(a)在(0,+∞)上单调递增, 而m(1)= 0,m(a)≥0⇔m(a)≥m(1),a的取值范围为[1,+∞).

评注本题中同时含有指数型函数与对数型函数,整理后不等式两侧分别是指数型函数与对数型函数,并且指数型函数是凸函数,对数型函数是凹函数,结合图像,求出公切点,只需在公切点处凸函数值大于等于凹函数值,便可保证整个凸函数图像位于凹函数图像上方.

通过以上解法我们看到,2020年高考山东卷导数大题仍保持一贯的高考题风格:入口宽,逐步递进,拾阶而上.试题设计立足课本,背景公平,设问通俗,解答灵活,充分体现高中数学核心素养.