一道解析几何自招试题的探究与思考*

北京市第十二中学高中部(100071) 刘 刚

1 试题

题目如图1,在平面直角坐标系xOy中,已知点F1、F1分别为椭圆E:=1(a ＞b ＞0)的左、右焦点,A、B分别是椭圆E的左、右顶点,D(1,0)为线段OF2的中点,且

图1

(1)求椭圆E的方程;

(2)若M为椭圆E上的动点(异于A、B),连接MF1并延长交椭圆E于点N,连接MD、ND并分别延长交椭圆E于点P、Q,连接PQ,设直线MN、PQ的斜率存在且分别为k1、k2,试问是否存在常数λ,使得k1+λk2= 0 恒成立? 若存在,求出λ的值;若不存在,说明理由.

这是2018年武汉大学自主招生中的一道试题,考查了椭圆的标准方程、几何性质、直线与椭圆的位置关系以及定值问题,考查了方程、转化与化归等数学思想以及坐标法的应用,检验了数学运算、逻辑推理等数学核心素养.试题平中见奇,解法多样,内涵丰富,是一道具有研究性学习价值的好题.

2 解法探究

(2)解法1设M(x1,y1),N(x2,y2),P(x3,y3),Q(x4,y4),则直线MD的方程为x=+1,代入椭圆E的方程=1,整理,得所以y1+y3=从而得y3=所以x3=+1 =即点同理,可得点因为M,F1,N三点共线,所以即x1y2-x2y1=2(y1-y2).因为

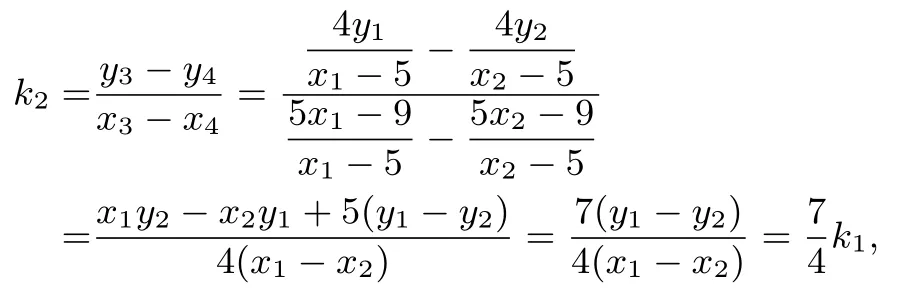
点评试题(2)问涉及多动点,这给学生解答带来了很大的困难,解决的基本方法还是坐标法,虽然解题过程中设出了M,N,P,Q这四个点的坐标,但通过分别联立直线MD、ND与椭圆E的方程并借助韦达定理,可以实现用M点坐标表示P点坐标以及N点坐标表示Q点坐标,从而达到消元的目的,体现了设而不求的思想方法.

解法2设直线MP、NQ的斜率分别为k3、k4,因为直线MP、NQ过点D(1,0),所以直线MP、NQ的方程分别为k3x-y-k3= 0,k4x-y-k4= 0.设直线PQ的方程为k2x-y+m= 0,又直线MN过点F1(-2,0),所以直线MN的方程为k1x-y+2k1=0,所以过M,N,P,Q四点的曲线系方程为

整理,得

与5x2+9y2-45=0 比较系数,得

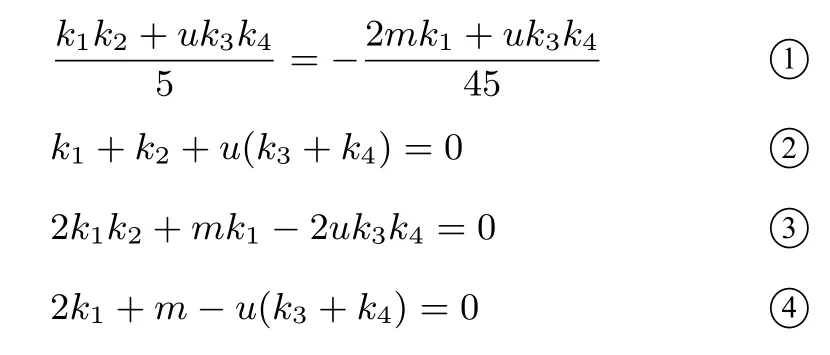
由①, 得10uk3k4=-2mk1-9k1k2, 代入③, 得m=.由②④,得k2=-3k1-m,所以k2=-3k1+即k1-=0,故存在满足条件的常数λ=

点评在解决圆锥曲线上四点问题时可借助曲线系方程, 具体为:设直线AB,CD的方程分别lAB(x,y)= 0,lCD(x,y)= 0, 直线AC,BD的方程分别lAC(x,y)= 0,lBD(x,y)=0,则过A、B、C、D四点的二次曲线系方程可以设成lAB(x,y)lCD(x,y)+λlAC(x,y)lBD(x,y)= 0,然后化成一般式方程再与已知圆锥曲线方程比较系数求解,体现了变换的思想和整体处理的解题策略,提高了解题效率.

解法3设则

同理,

点评解法3 先借助椭圆的参数方程表示出点M、N、P、Q的坐标,接下来借助三角公式进行逻辑推理,并适时进行消元.在解答过程中虽然对运算有一定的要求,但解题思路明确,易操作,不失为一种好方法.参数法是解决椭圆问题的一种常用方法.

3 思考

解析几何是一门用代数方法研究几何问题的学科,代数是工具,几何是本质,解答时通常遵循先几何后代数的解题策略.本道试题能否用几何法解决? 具有怎样的几何背景?带着这样的思考,笔者进行了深入的研究,下面先给出高等几何中的几个定义和性质.

(1)极点与极线

(Ⅰ)几何定义.如图2,点P不在圆锥曲线Γ 上,过点P引两条割线与Γ 依次交于A、B、C、D四点,直线AD与BC交于点G, 直线AC与BD交于点H, 连接PG,HG,PH,则直线HG为点P对应Γ 的极线,直线PG为点H对应Γ的极线,直线PH为点G对应Γ 的极线.若点P在圆锥曲线Γ 上,则过点P的切线即为极线.

(Ⅱ)代数定义.已知圆锥曲线Γ :Ax2+Cy2+2Dx+2Ey+F= 0,则称点P(x0,y0)和直线l:Ax0x+Cy0y+D(x+x0)+E(y+y0)+F=0 是Γ 的一对极点和极线.

图3

(2)调和点列与调和线束

(Ⅰ)定义.一条直线上的四个点A、B、C、D如果满足那么称A、B、C、D为调和点列,亦称B、D调和分割线段AC.过调和点列A、B、C、D所在直线外一点P,向A、B、C、D引四条线束(射线),称这四条线束PA、PB、PC、PD为调和线束.

(Ⅱ)性质.如图3, 设直线l与调和线束PA、PB、PC、PD分别交于点A′、B′、C′、D′,则A′、B′、C′、D′为调和点列.

证明由A、B、C、D是调和点列,得即于是

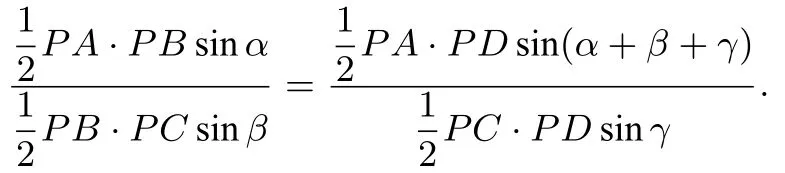
(3)完全四边形及性质

(Ⅰ)定义.我们把两两相交,且没有三线共点的四条直线及它们的六个交点所构成的图形,叫做完全四边形.如图4,直线ABE、BCF、ECD、ADF两两相交于B、C、D、E、F、A六点,则四边形ABECFD为完全四边形,线段AC、BD、EF为其三条对角线.

(Ⅱ)性质.完全四边形的一条对角线所在直线与其他两条对角线相交, 则这条对角线被交点调和分割.如图5,在完全四边形ABECFD中, 直线AC与BD交于点G, 与EF交于点H, 则(或AG·CH=AH ·CG).

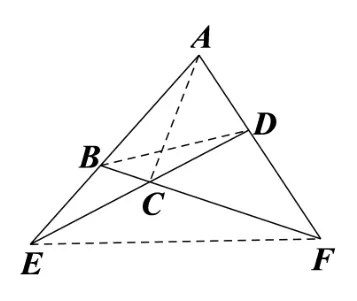
图4

证明若BD//EF,如图5,则得证.若BD与EF不平行,如图6,设这两条直线交于点M,对ΔACD及点B应用塞瓦定理,得

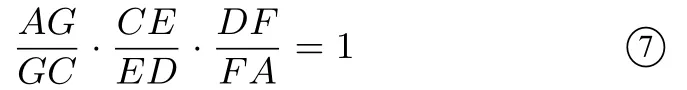
对ΔACD及割线EHF应用梅涅劳斯定理,得

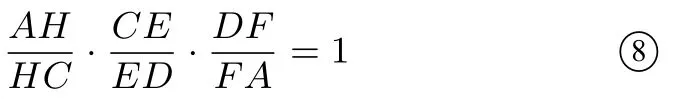
⑦÷⑧, 得类似地, 还可证明成立.

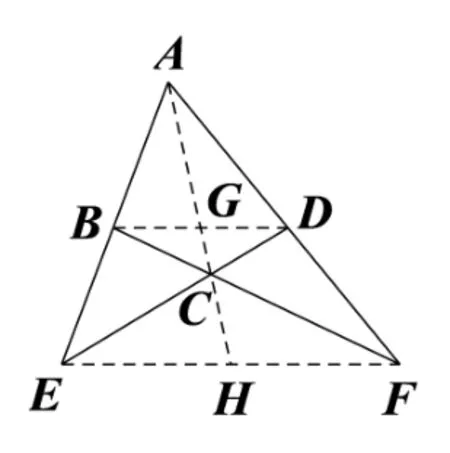
图5

图6

有了以上知识的介绍,下面从几何的角度再认识一下这道试题:

图7

解法4如图7,设直线MN与PQ交于点R, 直线MQ与NP交于点S, 则直线RS是点D对应椭圆E的极线,其方程为x= 9.设直线RS与x轴交于点H,直线PQ与x轴交于点T,直线NQ与RS交于点G, 由此可得完全四边形NMRQSP.于是D、G调和分割NQ,连接DR,所以射线RN、RD、RP、RH为调和线束,于是x轴与调和线束的交点F1、D、T、H为调和点列, 所以解得而k1=tan ∠RF1H=,k2=tan ∠RTH=所以故存在满足条件的常数λ=

点评几何法揭示了问题的本质,体现了过程的简洁性.将试题一般化,并类比双曲线、抛物线,可以得到圆锥曲线的一个统一结论.

定理如图8,已知P是圆锥曲线Γ 的轴l上一点(P不在Γ上),过P引两条直线与Γ 依次交于点A、B、C、D,直线AB与CD交于点R, 直线AD与BC交于点S,直线RS与l交于点H,直线AB与l交于点M, 直线CD与l交于点N,则(请读者参考解法4,限于篇幅不再赘述)

图8

高考及自招试题都是集体智慧的结晶,具有典型性与创新性等特点,在研究这些考题时,除了关注通解通法以外,还要注意挖掘其背后所蕴含丰富、深刻的数学背景,在这一过程中,体现出了对数学本质认识的“螺旋式”上升,提升了核心素养.

以下试题供读者练习:

1.(2018年徐州一模)如图9, 在平面直角坐标系xOy中,已知椭圆= 1(a ＞b ＞0)的离心率为且过点,F为椭圆的右焦点,A,B为椭圆上关于原点对称的两点,连接AF,BF分别交椭圆于C,D两点.

(1)求椭圆的标准方程;

(2)若|AF=|FC|,求的值;

(3)设直线AB,CD的斜率分别为k1,k2, 是否存在实数m, 使得k2=mk1, 若存在, 求出m的值; 若不存在,请说明理由.

图9

2.(2017年数学联赛湖北预赛)过抛物线y2= 4x的焦点F的直线交抛物线于M、N两点,E(m,0)为x轴上一点,ME、NE的延长线分别交抛物线于点P、Q.若MN、PQ的斜率k1、k2满足k1=3k2,则实数m的值为____.

答案:1.(1)= 1;(2);(3)存在实数2.m=3.