富水隧道围岩稳定性的数值模拟研究

孙学超

(中铁十九局集团第三工程有限公司，辽宁 沈阳 110136)

0 引言

进行富水区隧道开挖时，经常会遇到突水突泥的情况。在富水区开挖隧道不仅需要考虑地下水对隧道力学参数的减损，同时还需要考虑流固耦合作用对隧道围岩产生的力学效应。关于流固耦合作用对隧道围岩稳定性的影响问题逐渐引起相关人员的关注。李术才等[1]开发了可用于模拟准三维平面应力和平面应变的新型流固耦合模型试验系统，该系统既能保证试验要求的密封性，又便于可视化观察施工过程中海底隧道围岩渗流、变形特征。采用该流固耦合模型试验系统，以及独立研制的新型流固耦合相似材料并依托青岛胶州湾海底隧道开展流固耦合模型试验研究，揭示海底隧道施工过程中洞壁压力和围岩位移场、渗流场等的变化规律。荣传新等[2]应用统一强度理论和弹塑性损伤力学模型，推导出立井混凝土井壁弹性区和塑性损伤区应力的解析表达式，以及井壁承受的地下水压与塑性损伤区半径之间关系的解析表达式。单鹏飞等[3]通过位移反演方法对区域地应力特征进行理论分析，建立研究煤岩内部裂隙时空演化规律的力学实验系统，设计了区域地应力作用下裂隙煤岩流固耦合计算模型，初步揭示裂隙煤岩流固耦合特性。姚多喜等[4]根据五沟煤矿1018工作面地质及水文地质条件，应用三维快速拉格朗日(FLAC-3D)流固耦合分析模块，采用变渗透系数方法，对该工作面底板岩体采动渗流应变机制进行数值模拟研究。李顺才等[5]利用承压破碎岩石非Darcy渗流的渗透特性试验规律,对破碎岩体渗流动力系统进行了应力场与渗流场耦合的分岔行为研究。

流固耦合作用对隧道围岩的安全稳定性具有重要的影响。杨林地区地下水丰富，围岩稳定性相对较差。本文采用MIDAS/GTS NX流固耦合模块建立计算模型，分析研究流固耦合作用对围岩应力场和位移场的影响规律，为隧道开挖后的支护条件提供可靠依据。

1 模型建立

隧址区地下水充足，岩性多样，裂隙较发育，岩体多为碎裂状，围岩等级较低，稳定性差，隧道开挖时产生严重的变形。根据工程地质勘测资料显示，隧道围岩主要含大理岩、石灰岩、花岗岩以及混合岩等多种岩性的岩体。隧道横断面为马蹄形，采用喷锚支护。

由于隧道轴向长度远大于横断面尺寸，因此，在分析隧道应力场和位移场时仅对断面方向进行研究。隧道宽度方向左右各取3倍洞跨，模型地边界距离隧道底板2倍洞高，顶部取至地表，距离隧道拱顶140 m。计算模型及测点布设见图1，图中A点代表隧道底板测点，B点代表设定拱顶测点，C、D点分别代表隧道左右边墙测点，E点代表地表沉降测点。计算参数见表1，模型计算参数均取自室内试验。

图1 数值计算模型及测点布设

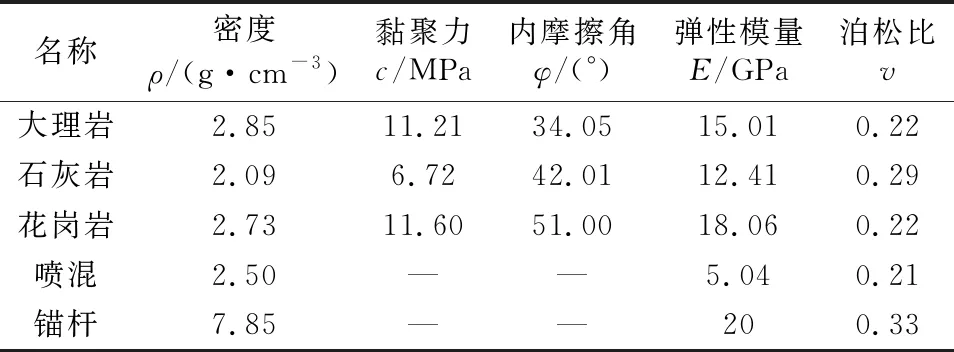
表1 模型计算参数

由于本文试验参数均由Mohr-Columd强度准则计算得出，数值模拟过程中假定岩体为各向同性材料，地层之间的应力-应变关系均在弹性范围内变化。根据连续介质力学中的位移边界、应力边界以及混合边界条件的设定原则，模型左右两侧对水平方向位移进行约束，底面位移对数值方向进行约束，顶部为自由面。用模型进行流固耦合计算时，假设隧道开挖前各岩体均处于饱和状态，渗流边界水头为距离隧道拱顶140 m位置，左右两侧和底部均假定为不透水边界，设定孔隙水压力值为零[6]。在隧道拱顶、底板、左右边墙以及地表布设监测点，测点分布如图所示，并与实际测量结果进行对比分析。

2 围岩应力场分析

隧道开挖后，最大主应力分布如图2所示，可以看出隧道周边的应力场在有无渗流条件下均发生了应力重分布现象，且在隧道周边区域较为明显。其原因可能是由于隧道开挖后破坏了原有岩层的应力场，使隧道周边围岩向开挖面积聚。对比发现，无渗流条件下的最大主应力为5.72 MPa，渗流条件下的最大主应力为1.77 MPa，且渗流条件下整体最大主应力均较无渗流条件下小，其原因可能是由于地下水渗流作用使岩体自身强度减弱，加之开挖后裂隙扩大，渗流进入岩体内部的更多，致使岩体的最大主应力较小。因此，在地下水发育区域修建隧道等地下工程时，应及时进行支护或超前支护。

图2 最大主应力分布云图

渗流条件下，隧道开挖前和开挖后的孔隙水压力等值线如图3所示，可以看出，隧道开挖前，孔隙水压力成层分布；开挖后，孔隙水压力逐渐向隧道开挖面转移，成漏斗状分布，与实际情况类似。隧道开挖打破了原岩应力和孔隙水压力的分布，使围岩向隧道内部调整和转移，同时形成开挖松动区，使松动区围岩损伤产生裂隙，地下水在重力的作用下，沿开挖裂隙渗流，最终使得开挖形成临空面。隧道开挖也导致开挖区域周边的位置水头迅速下降，渗流最终成漏斗状分布。

图3 孔隙压力等值线云图

3 围岩位移场分析

3.1 竖直方向位移分析

隧道开挖后，围岩位移场竖直(Z)方向位移等值线如图4所示，其中竖直向上为正值，竖直向下为负值，从图中可以看出，渗流状态下竖直方向的位移变化量明显大于无渗流状态的变化量，渗流情况下最大竖直方向位移值为72.27 mm，发生在隧道底板处，拱顶最大沉降为67.16 mm。无渗流状态下最大竖直方向位移发生部位与渗流情况相同，其中隧道底板隆起值为61.03 mm，拱顶沉降值为59.21 mm。从位移分布等值线图可以看出，渗流状态下的整体沉降范围大于无渗流状态下的整体沉降。

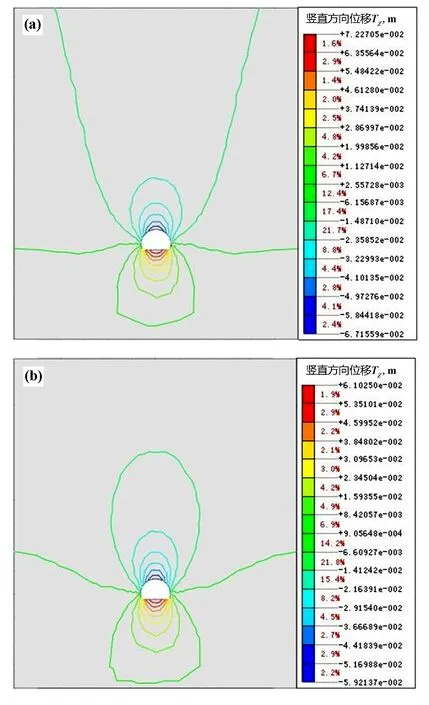
图4 竖直方向(Z)位移等值线云图

如图5所示，分别为拱顶沉降和底板位移随开挖时步变化曲线，根据现场实测数据与渗流和无渗流情况进行对比分析可知，随着开挖时步的增加，拱顶沉降和底板位移均逐渐增大，并且逐渐趋于平缓，渗流状态下拱顶和底板位移均大于无渗流状态。现场实测数据与渗流状态较为接近。现场条件复杂，操作流程、现场环境以及检测仪器的误差导致实测数据与渗流状态下有些误差。

图5 竖直方向(Z)位移曲线随开挖时步分布曲线

3.2 水平方向位移分析

隧道开挖后，围岩位移场水平(Z)方向位移等值线如图6所示，其中水平向右为正值，水平向左为负值，渗流状态下水平位移略大，但与无渗流状态相比变化不大。渗流状态下最大水平位移值为30.65 mm，发生在隧道左边墙位置，右边墙水平位移为30.58 mm，左右两侧水平位移均向隧道内部收敛，且大体成对称分布。无渗流状态下水平位移的总体变化情况与渗流状态类似，左侧边墙最大水平位移为29.74 mm，右侧边墙最大水平位移为29.95 mm。

图6 水平方向(X)位移等值线云图

如图7所示，分别为左边墙和右边墙水平位移随开挖时步变化曲线，根据现场实测数据与渗流和无渗流情况进行对比分析可知，随着开挖时步的增加，左边墙与右边墙收敛值均随着开挖时步的增大而增加，并且逐渐趋于平缓。渗流状态下的水平位移变化量略大于无渗流状态，但变化并不明显。现场实测数据与渗流状态较为接近，因现场情况复杂，操作流程，现场环境以及检测仪器的误差导致实测数据与渗流状态下有些误差。

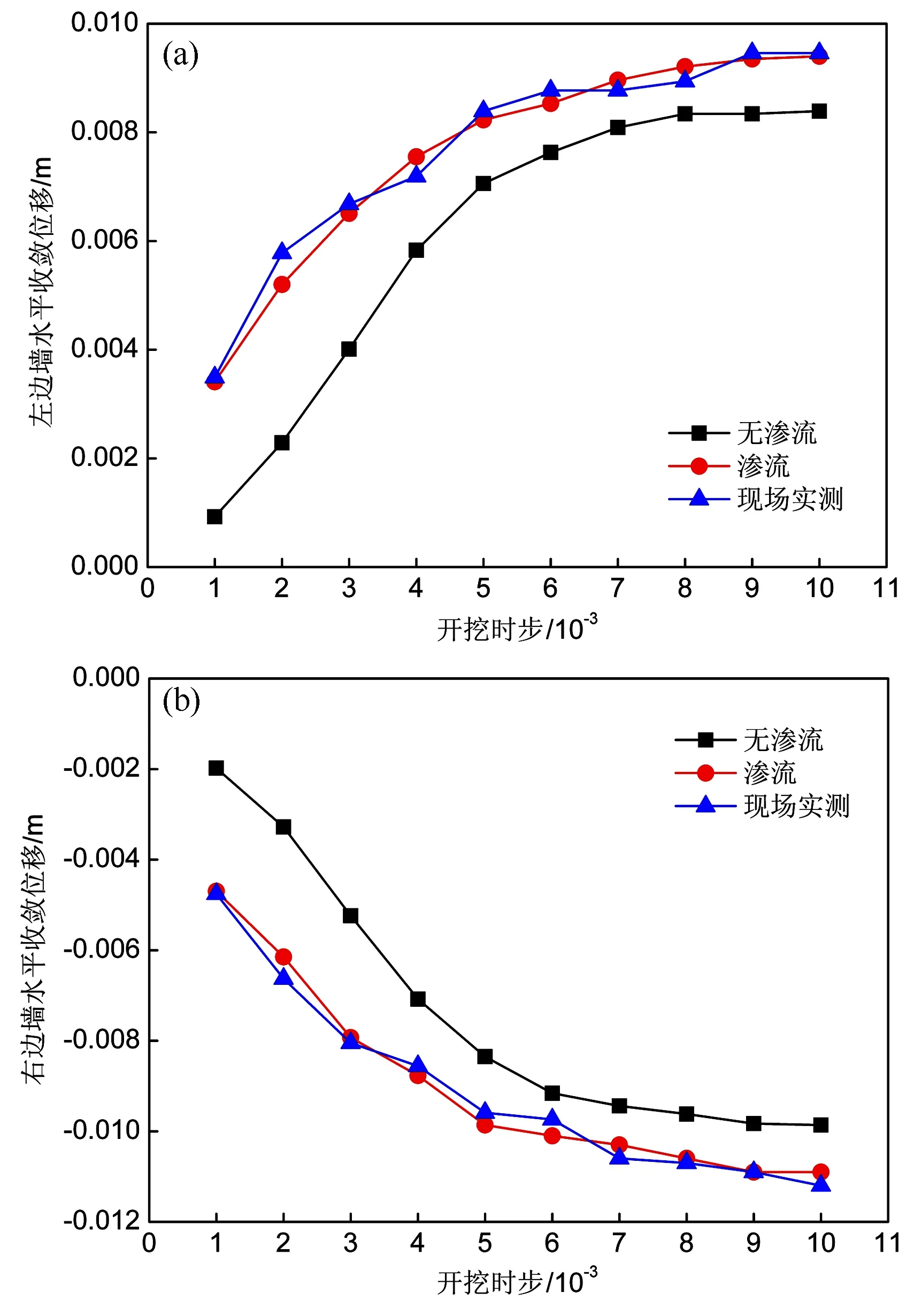
图7 水平方向(X)位移随开挖时步分布曲线

3.3 地表沉降分析

如图8所示，地表沉降最大值位于隧道开挖中心处，整体呈漏斗状塌陷，深流状态较无渗流状态变化明显。在无渗流状态下时，其原因可能是由于开挖导致拱顶下沉，随之产生连带反应，致使地表下沉。而渗流状态更主要的原因是开挖导致大范围内的孔隙水压力减小所致。

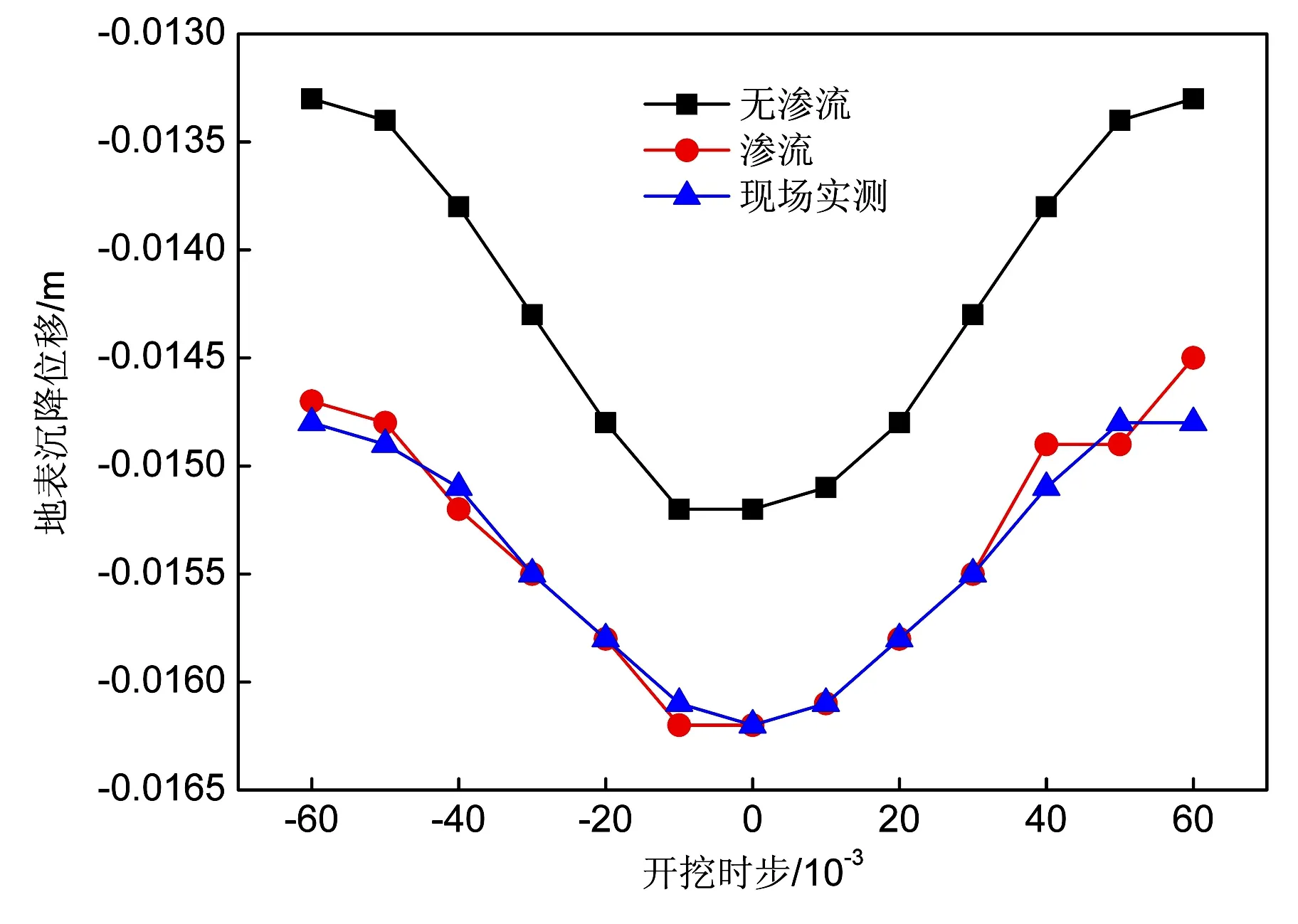
图8 地表沉降距隧道中心位移

4 结论

通过对杨林隧道考虑流固耦合与不考虑流固耦合数值模拟研究以及实测数据对比分析得到如下结论：

(1)渗流作用下隧道周围岩体应力重分布范围较无渗流状态下更大，由于水对岩体的渗流作用，导致岩体强度降低。渗流状态下最大主应力明显小于无渗流状态下的最大主应力。由此可见，渗流作用将给隧道围岩稳定性带来不利影响。

(2)隧道围岩变形研究可知，渗流作用对水平位移变化影响不大，其中渗流状态略大于无渗流状态。而渗流作用对竖直方向的位移变化情况影响较大，渗流作用下的拱顶沉降和底板隆起均明显大于无渗流状态。其中，隧道拱顶沉降位移从59.21 mm增加到61.75 mm，隧道底板隆起从61.03 mm增加到72.27 mm，左侧隧道边墙水平收敛从29.73 mm增加到30.64 mm，右侧隧道边墙水平收敛从29.95 mm增加到30.59 mm。

(3)根据地表沉降分析结果可知，在无渗流状态下，可能是由于开挖导致拱顶下沉，随之产生连带反应，致使地表下沉，而渗流状态更主要的原因是开挖导致大范围内的孔隙水压力减小所致。