高斯噪声特性区间ν -支持向量回归机
2021-01-08张仕光周婷刘超李源
张仕光,周婷,刘超,李源
(1.河南师范大学 计算机与信息工程学院,河南 新乡 453007;2.河南师范大学 国有资产管理处,河南 新乡 453007)
0 引言
支持向量回归模型已成功应用于风电场调度中的风速/风功率预报、金融领域中的股票预测等诸多领域,并吸引了人们的广泛关注[1-5]。设给定训练集Dl={(x1,y1),(x2,y2),…,(xl,yl)},其中xi=(xi1,xi2,…,xiL)∈RL,yi∈R(i=1,2,…,l),l为样本数量。假定Dl是某概率分布P(x,y)上选取的独立同分布的样本,给定损失函数为c(x,y,f(x))。
Vapnik、Cortes[1-2]提出ε-不敏感损失函数:
c(x,y,f(x))=|y-f(x)|ε,
(1)

Pν-SVR:s.t.ωT·φ(xi)+b-yi≤ε+ξi
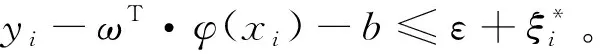
(2)
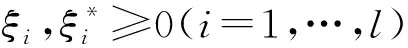
在实际应用中,很多经典的确定性模型和算法都假定数据中存在高斯误差特性来进行建模。2010年Wu等[8-9]提出基于Gaussian噪声影响的ν-支持向量回归模型(ν-support vector regression machine for Gaussian noise,简记为GN-SVR),并利用遗传算法和粒子群优化算法进行了求解。其原问题为:

(3)


(4)
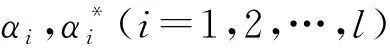
f(x)=ωT·φ(x)+b=

(5)

在实际应用领域中,若数据中存在高斯噪声特性,则利用模型GN-SVR可得到精确的预报值。但在某些领域,如风电场调度中的风速/风功率预报[10-15]、金融领域中的股票预测需要预报某个目标值的区间值[16],模型GN-SVR不能有效解决上述问题。
为了解决上述问题,本文在Gaussian噪声ν-支持向量回归模型的基础上,利用区间数方法研究了基于不等式约束的Gaussian噪声特性区间ν-支持向量回归模型。
1 Gaussian噪声特性区间ν-支持向量回归机
1.1 基本概念
首先引进区间数、区间数的二元关系运算等相关概念。
定义1[17-18]区间数(ai,Δai):设R为实数域,ai∈R为中心,Δai≥0为半径,区间数A=(ai,Δai)为:
A=(ai,Δai)=[ai-Δai,ai+Δai],
其中ai-Δai称为区间数A的左边界,ai+Δai称为其右边界。若区间数A的左边界等于其右边界,即Δai=0,定义区间数A为点区间。R上所有区间数的集合,记为I(R)。
定义2[18-19]设区间数A,B∈I(R),定义I(R)上的二元关系运算为:
A+B=(ai+bi,Δai+Δbi),
λA=(λai,|λ|Δai),∀λ∈R,
A-B=(ai-Δai-bi-
Δbi,ai+Δai-bi+Δbi)。
1.2 基于不等式约束的Gaussian噪声特性区间ν-支持向量回归机
设给定包含区间值的训练集
Tl={(X1,Y1),(X2,Y2),…,(Xl,Yl)}
(6)

基于不等式约束的Gaussian噪声特性区间ν-支持向量回归机(Intervalν-support vector regression model of Gaussian noise characteristics with the inequality constraints,简记为GNI-SVR)的原问题可描述为:
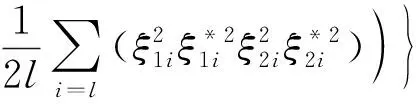
(7)
PGNI-SVR:s.t.
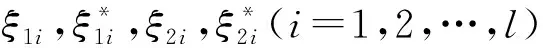
命题1基于不等式约束Gaussian噪声特性区间ν-支持向量回归机原问题(7)关于ω的解存在且唯一。
定理1 基于不等式约束Gaussian噪声特性区间ν-支持向量回归机原问题(7)的对偶问题为:

(8)
DGNI-SVR:s.t.
其中0<ν≤1,惩罚因子C>0是常数。
证明引进Lagrange泛函L(ω,B,α,α*,ξ,ξ*,η,η*,ε)得:
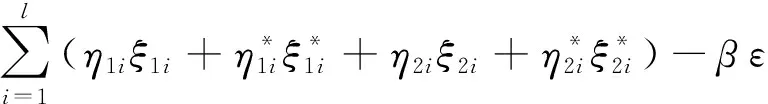
(yi+Δyi)-ε-ξ1i)+
(yi-Δyi)-ε-ξ2i)+
其中Lagrange乘子α,α*,η,η*,β≥0,为求L(ω,b,α,α*,ξ,ξ*,η,η*,ε)的极小值,分别对ω,b,ξ,ξ*,ε求偏导数。由
得:
把上述极值条件代入L(ω,b,α,α*,ξ,ξ*,η,η*,ε),并对α,α*求极大值,可以得式(7)的对偶问题(8)。
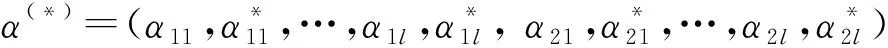
令
当j∈S+,k∈S-,则
基于不等式约束的Gaussian噪声特性区间ν-支持向量回归机的决策函数为:

(9)

2 结论
当Δxi=0,Δyi=0时,模型GNI-SVR即为模型GN-SVR。
在风电场调度、金融领域预测中,根据数据集Tl的信息可计算得Δxi,Δyi,ρ(Δxi),利用模型GNI-SVR可得风电场调度中的风速/风功率预报、金融领域中的股票预测所需预报某个目标值的区间值。
