学习空间理论的ACM竞赛关键学习路径算法
2021-01-08何秋红孙文郑文彬朱月秀
何秋红,孙文,郑文彬,朱月秀
(1.闽南师范大学 计算机学院,福建 漳州 363000;2.闽南师范大学 福建省粒计算及其应用重点实验室,福建 漳州 363000;3.汕头大学 理学院,广东 汕头 515000)
学习空间理论(Learning Spaces Theory,简称LST)源于知识空间理论(Knowledge Spaces Theory,简称KST),是由美国数学心理学家Jean-Claude Falmagne和比利时数学心理学家Jean-Paul Doignon(以下简称JCF和JPD)于1985年提出并完善的组合数学理论,为用机器自动评估学生知识的应用提供了一个完整的理论框架。它通过分析学生对某个专业领域中一系列精挑细选的难易程度不同问题的解答情况,尽可能精确而高效地判定学生对该领域知识和技能的掌握程度。后来发现知识评估机器其实可以作为一种教学技术的核心组件,因为准确地判断学生的知识状态正是教学过程的关键一环,从而把焦点从评估转向教学,就引出了一个特殊的知识空间,即“学习空间”[1-2]。JCF和JPD不仅提出了理论,还开发了体现这一理论的数学教学软件ALEKS(Assessment and Learning in Knowledge Spaces,https:∥www.aleks.com)。目前ALEKS教学软件提供数学、化学和物理课程,用以评估学生在这些科目的知识状态并指导他们的学习过程。这套系统已经在数千所学校的100门以上的课程中得到广泛应用,数百万学生因此在某些专业领域受益。受到ALEKS的启发,还诞生了一些类似的系统:RATH(1998)、APeLS(2002)、iClass(2008)、MedCAP(2009)、Lee(2014)等[3-4]。
国内关于学习空间理论研究主要有三个方面:(1)知识空间理论扩展的研究。研究员孙波于2004年对知识空间理论进行扩展,提出包含技能结构、技能空间以及技能层次相关概念的扩展知识空间理论,并概述该理论在测评系统中的相关运用[5]。同年,孙波提出了基于扩展知识空间理论的自适应测评的详细步骤,并对其中的关键过程做了进一步的优化[6]。2006年孙波的合作者傅骞按照扩展知识空间理论的观点,提出新一代教育资源平台应该把资源分成问题对象、技能(知识点)对象和学习对象三个既相对独立又密切联系的部分,从而使教育资源库不再单一地为教师的教学服务,还为学生的自主学习、自我评价服务[7]。(2)部分学者致力于应用该理论到辅助教学。比如应用学科已有计算机[8-10]、物理化学[11-13]、语文英语[14]等。为国内研究者更好地掌握应用学习空间理论,JCF和JPD所著的学习空间中译本已于2016年由胡祥恩教授和王泰合作完成[15]。2019年,牟智佳等开发了基于知识空间理论的学习预警工具[16]。(3)部分学者把学习空间理论与其他学科建立联系,高纯从粒计算的视角将知识空间理论与粗糙集理论建立起有意义的联系[17];2019年,李进金教授综述了通过知识基建立知识空间和形式背景之间的联系[18]。
目前学习空间理论应用主要集中在逻辑性强的理工专业领域的学习和教学,但是该理论的应用前景非常远大,它还可以用于竞赛。竞赛比教学更具挑战性,因为竞赛综合了多门专业课知识,不仅知识点多而且难度大,例如ACM考核知识点达300多个。因此,应用学习空间理论对竞赛解答情况分析尤其重要。
主要贡献包括4个方面:
1) 推测关系确定题目难度等级;
2) 提出两种方案:学习路线方案和学习路径方案:学习路径是最大链,一次掌握一个问题;学习路线并非最大链,一次可能掌握两三个问题,比路径粒度更粗。当问题规模很大时选择知识基导出若干学习路线更快速,且无须算法,操作更方便;
3) 设计MaxPath算法查寻关键、一般和个别学习路径,实验结果证明关键学习路径适合大众认知过程;
4) 关键学习路径结合OJ平台创新评价机制激发做题兴趣和挑战高难题,并用于评估选手水平,为后期重现赛和新赛定制个性化高效训练计划。
1 ACM竞赛知识
ACM竞赛是国际计算机协会(Association for Computing Machinery,ACM)组织的年度赛,始于1970年,是全球历史最悠久、规模和影响力最大的国际大学生计算机程序设计竞赛,被誉为计算机软件领域的奥林匹克。在2018-2019赛季,全球6大洲的115个国家和地区,共有3 233所大学的52 709名学生、5 411名教师、参加ACM-ICPC的各级预赛。根据规则,为了保证比赛的公平公正,每个学生每年只能参加2个赛点的比赛,终生只能参加5次大赛、2次世界总决赛,这些规则为选拔更多计算机优秀人才创造了条件,使大赛成为培养未来计算机领军人物的重要平台之一。
受此启发,中国2015年始办大学生程序设计竞赛(China Collegiate Programming Contest,简称CCPC),CCPC是由教育部高等学校计算机类专业教学指导委员会主办的面向全国高校大学生的年度学科竞赛,旨在激发学生学习计算机领域专业知识与技能的兴趣,鼓励学生主动灵活地运用计算机知识和技能解决实际问题,有效提升算法设计、逻辑推理、数学建模、编程实现和计算机系统能力,培养团队合作意识、挑战精神和创新能力。自从2015年首届CCPC竞赛以来,赛事规模发展迅猛,已经有国内600余所高校的20 000余名大学生和1 500余名一线教练参与赛事,竞赛影响力持续提升,为我国IT业的发展培养和选拔了大批人才。
ACM考核的知识点涵盖四部分:(1)程序设计语言:输入、处理、输出;(2)数据结构:线性表、树、图;(3)算法:模拟、数论、组合数学、贪心、动态规划、高级数据结构、计算几何、博弈论;(4)程序设计解题策略:特定数据结构或者优化算法。竞赛题一般采用六级难度:Ⅰ简单题:程序设计语言题。Ⅱ准简单题:数据结构题。Ⅲ中等难度偏下:基础算法、数学题。Ⅳ中等难度:算法、数学综合题。Ⅴ中等难度偏上:含解题策略的算法、高级数学题。Ⅵ难题:高级综合算法及复杂含解题策略的算法、大代码量的模拟题。(本段引自ICPC亚洲第一训练委员会吴永辉主任课件)
2 学习空间理论基本定义在ACM竞赛的应用
JCF和JPD认为某一专业领域知识可以量化为精心设置的一系列难易不同问题,所有问题称为域,用Q表示,学生能够解决某个问题表示掌握了相应知识,因此问题的设置具有代表性。学生在理想条件下能正确解答的部分问题集构成一个知识状态,多个知识状态加上Q和空集ø形成知识结构,若有限知识结构满足封闭性就是知识空间,若知识空间还满足两个公设:学习的顺畅性(Learning Smoothness)和学习的持续性(Learning Consistency),称为学习空间。
每场比赛命题组一般会出8~13题。赛后有最终排行榜(解答情况),先按答对题数排名,题数相同按做对题目时间总和排名,总时间小的排前,若答对题目多次提交才通过,每一次未通过的提交要加20分钟罚时,罚时加到总时间。根据解答情况把每队选手的答对题集转为一个知识状态,所有选手的知识状态加上ø和Q构成ACM知识结构,在该知识结构上做封闭运算得到ACM知识空间,对知识空间应用学习空间理论定理补充部分知识状态张成ACM学习空间。
2.1 ACM解答情况数据集
数据集来源于2019年7月7日ACM-CCPC江西省程序设计大赛,该大赛由中国教育部计算机类专业教学指导委员会、中国大学生程序设计竞赛组委会主办,南昌大学承办,是江西省首届CCPC省赛,省内高校83支队伍展开激烈角逐,同时还吸引了来自省外高校的21支队伍参加,一共有104支队伍,每支有三名队员。比赛出11道题目A-K组成问题域Q,A:Cotree联合树;B:Math数学;C:Trap陷阱;D:Wave波浪;E:Packing包装;F:String字符串;G:Traffic交通;H:Rng随机数发生器;I:Budget预算;J:Worker工人;K:Class上课。采用二进制表示和存储ACM数据集,选手答对某道题记录为1,答错为0,从而得到选手在各道题的解答情况。例如,某队在11道题中答对前五题和最后题,该队知识状态为[1,1,1,1,1,0,0,0,0,0,1]。将解答情况转换为形式背景,如表1所示。
2.2 ACM数据集的推测关系和题目难度等级
推测关系表示问题间的位次(precedence)关系,问题有高低位次之分,低位次是高位次的基础,因而掌握高位次问题也就可以解决低位次问题[19]。从表1得知问题域Q={A, B, C, D, E, F, G, H, I, J, K}的知识空间X={ø, {K}, {F, K}, {I, K}, {F, I, K}, {F, J, K}, {I, J, K}, {F, I, J, K}, {F, G, J, K}, {D, F, I, J, K}, {F, G, I, J, K}, {D, F, G, I, J, K}, {A, D, F, G, I, J, K}, {D, F, G, H, I, J, K}, {A, D, F, G, H, I, J, K}, {A, C, D, F, G, H, I, J, K}, Q},共17个知识状态。公设[19]:如果K是Q的一个属于族X的非空子集,那么K中存在某个q,使得K{q}是X的一个状态。根据公设X增加了两个知识状态,得到学习空间X’=X∪{A, B, C, D, F, G, H, I, J, K} ∪ {A, C, D, E, F, G, H, I,J, K},共19个知识状态。计算可得学习空间推测关系:∩KK={K};∩KF={F, K}⟹KF;∩KI={I, K}⟹KI;∩KJ={J, K}⟹KJ;∩KG={G, K, F, J}⟹KG, FG, JG;∩KD={D, K, F, I, J}⟹KD, FD, ID, JD;∩KA={A, K, F, I, J, G, D}⟹KA, FA, IA, JA, GA, DA;∩KH={H, K, F, I, J, G, D}⟹KH, FH, IH, JH, GH, DH;∩KC={C, K, F, I, J, G, D, A, H}⟹KC, FC, IC, JC, GC, DC, AC, HC;∩KB={B, K, F, I, J, G, D, A, H, C}⟹KB, FB, IB, JB, GB, DB, AB, HB, CB;∩KE={E, K, F, I, J, G, D, A, H, C}。E推测关系同B略。参见表2和图1。
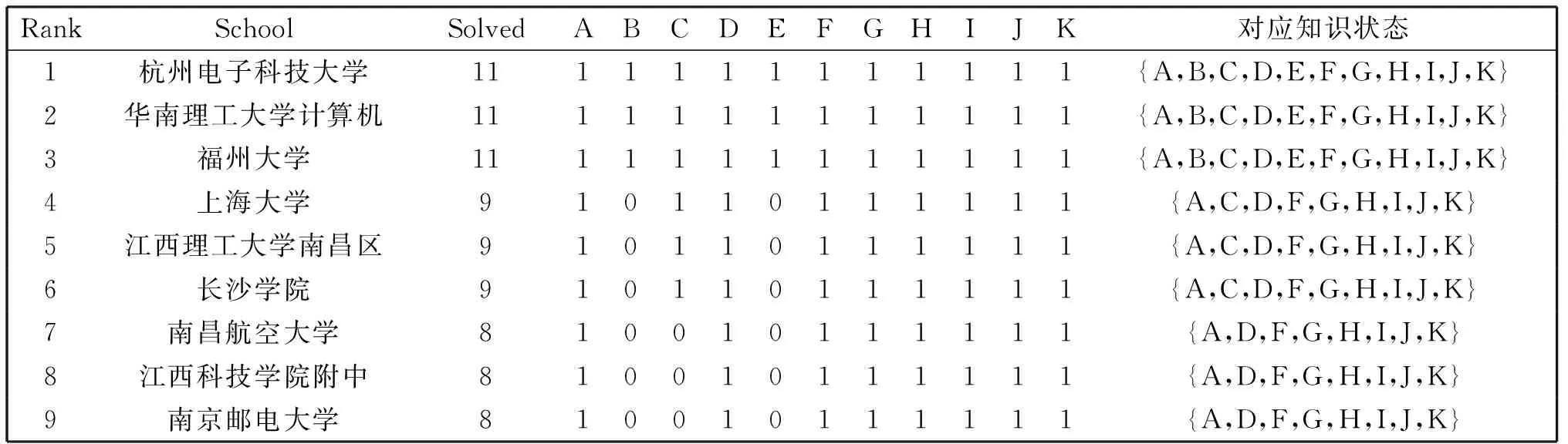
表1 2019 CCPC江西省程序设计正式赛排行榜
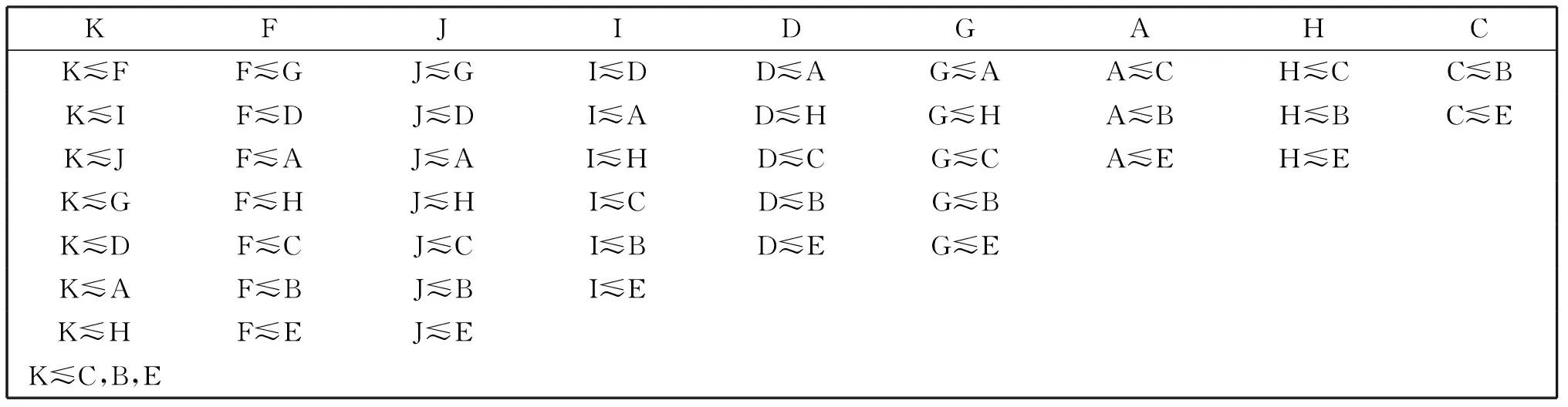
表2 竞赛题的推测关系
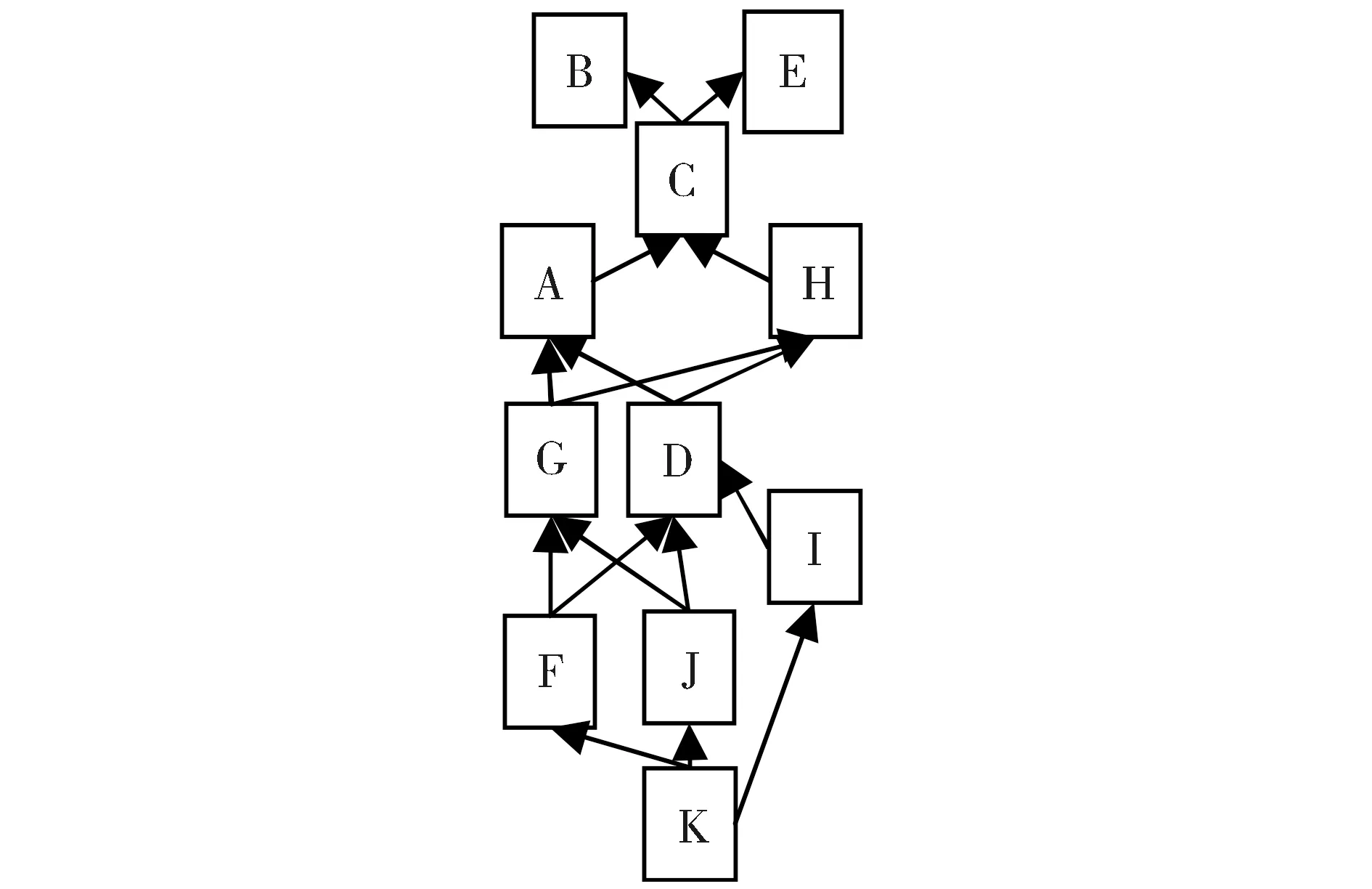
图1 竞赛题的推测关系Fig.1 Surmise relation of contest questions
特别注意的是图1中I和G没有推测关系,但I和D有推测关系,故I无法严格划分难度等级,把I难度稍微提高,得到ACM数据集的推测关系学习路线:K→F,J→I,G,D→A,H→C→B,E。根据该路线结合命题组的试题分档规则分七级难度:Ⅰ中下简单题K是基础程序设计解方程。Ⅱ中等简单题F是程序设计字符串加乘法原理、中简单题J是按比例分配。Ⅲ中上简单题I是程序设计浮点数。Ⅳ中等难度偏下D和G都是基础数据结构线性表加上基础算法暴力法。Ⅴ中等难度A是数据结构树加上深度优先算法、H是数学求逆元。Ⅵ中等难度偏上C是高级数学互质、容斥原理加上暴力法。Ⅶ难题B是高级数据结构图上随机游走的模型加上概率动态规划法、难题E是高级算法动态规划法。
2.3 ACM数据集的知识基学习路线
下面定义四个重要概念:
定义1学习路径[19]。一个知识结构(Q,K)(有限或者无限)的学习路径是偏序集(K,⊆)中一个最大链L。
定义2最大链[19]。对于所有的C,C’∈L,C⊆C’或者C’⊆C,对于某个状态链L’,只要L⊆L’,都有L=L’。
一个最大链必然包含ø和Q。例如,当有限域Q包含m个问题时,一条学习路径的形式可能是这样:ø⊂{q1}⊂{q1,q2}⊂ …⊂{q1,q2, …,qm}=Q,即满足任意相邻知识状态中右状态真包含左状态的从ø(零知识)到Q(所有知识)最长知识状态序列,从ø到Q之间的学习路径有很多条。
定义3关键学习路径(critical learning path)[12]。根据知识状态的数量通过一系列概率计算,具有最大概率的学习路径。
关键学习路径是反映学生群体学习某领域知识情况的重要方面。
定义4学习路线。一个知识结构(Q,K)(有限或者无限)的学习路线是偏序集(K,⊆)中一个非最大链。
知识空间的基简称知识基,它是知识空间的最小生成组,蕴含了知识空间所有信息。所有问题的原子得到知识基Base={{K}, {F, K}, {I, K}, {F, J, K}, {I, J, K}, {F, G, J, K}, {D, F, I, J, K}, {A, D, F, G, I, J, K}, {D, F, G, H, I, J, K}, {A, C, D, F, G, H, I, J, K}, {A, B, C, D, F, G, H, I, J, K}, {A, C, D, E, F, G, H, I, J, K}},共12个状态。当问题规模很大时,可以考虑由基直接得到类似学习路径的学习路线,因为知识基通常规模比知识空间小很多,可以节约计算量和存储空间。学习路线比学习路径粒度更粗,本案得到4条学习路线参见表3。
2.4 知识结构图
图2采用R语言绘制知识结构图:fs<-kfamset(set(set("K"), set("I", "K"), set("F", "K"),set("F", "I", "K"), set("F", "J", "K"), set ("I", "J", "K"), set("F","I", "J", "K"), set("F", "G", "J", "K"), set("D", "F", "I", "J", "K"), set("F", "G", "I", "J", "K"), set("D", "F", "G", "I", "J", "K"), set("A", "D", "F", "G", "I", "J", "K"), set("D", "F", "G", "H", "I", "J", "K"), set("A", "D", "F", "G", "H", "I", "J", "K"), set("A", "C", "D", "F", "G", "H", "I", "J", "K"), set("A", "B", "C", "D", "F", "G", "H", "I", "J", "K"), set("A", "C", "D", "E", "F", "G", "H", "I", "J", "K")))if(require("Rgraphviz")){plot(fs)}。
2.5 ACM数据集的MaxPath学习路径算法
为了查寻学习路径,首先用一个有向图模型G=(V, E)来描述知识空间图,即从图2抽象出数据结构的有向图,其中:V是图G中顶点的集合,E是图G中边的集合,每个顶点表示一个知识状态,每条边表示两个距离最近知识状态的真包含,边上的权值表示上面知识状态的队伍数,如图3所示,v2到v4({K}到{F, K})权值为4,表示有四支队伍成绩为{F, K}。V(G)={v1,v2, …,v19},E(G)={

图2 竞赛题的知识结构图Fig.2 The knowledge structurediagram of contest questions

表3 学习路线与学习路径比较

图3 带权有向图GFig.3 Directed graph with weight
MaxPath算法思想:设置一个集合Set存放已经找到最长路径的顶点,Set的初始状态只包含源点v1(即ø),对vi∈V-Set,假设从源点v1到vi的有向边为最长路径。以后每求得一条最长路径v, …,vk,就将vk加入集合Set中,并将路径v, …,vk,vi与原来的假设相比较,取路径长度较大者为最长路径。重复上述过程,直到集合V中全部顶点加入集合Set中。该算法时间复杂度为O(n^2),属于多项式有效时间,其中n为顶点数。
MaxPath算法:查寻关键、一般和个别学习路径。
Input:竞赛题知识空间有向图
Output:从ø到Q的最长路径
1)初始化数组dist、path、num;
2) while(元素个数num 3) 在dist[n]中求最大值,其下标为k; 4) 输出dist[k]和path[k]; 5) 修改数组dist和path; 6) dist[k]=0表示已找到源点ø到顶点k的最长路径。 (注:数组dist[n]:每个分量dist[i]表示当前所找到的始点v1到终点vi的最长路径的长度。初态为v1到vi弧上权值;无弧dist[i]=-∞。 数组path[n]:path[i]是一个字符串,表示当前所找到的始点v1到终点vi的最长路径顶点串。初态为v1vi;无弧path[i]=“ ”,空串。) 首先,程序运行非带权图找到两条一般学习路径(非带权指所有边的权值为1)。其次,在带权图上分别查找更符合大众和少数人认知规律的关键学习路径和个别路径,还是应用MaxPath算法求解从ø到Q的带权最长路径。最多选手(权值总和最大)的学习路径就是关键学习路径,而最少选手(权值总和最小)的学习路径是个别学习路径。运行结果找到一条关键学习路径和一条个别学习路径,因此,加权学习路径比一般学习路径更收敛。 本次比赛共11题,每题答对得一分,104支队伍的平均分为5.298分,标准差为1.961,成绩服从正态分布,该场比赛成绩改变以往的宝塔状分布,尤其是K题,百分百通过,得到一致好评。以下结合学习空间理论的关键学习路径,指导如何在竞赛中提高大学生程序设计创新与解决实际问题的能力。 从实验结果得知各有五条学习路径和路线,共十条,如表3所示。分别以答对率降序学习路径和推测关系学习路线作为参考基准,若两个问题顺序与它们在参考基准的顺序前后相反称一个逆序,同级别问题或者两个无推测关系问题出现一前一后均不算逆序。首先,以答对率路径作为基准,关键学习路径:0逆序;个别学习路径3个逆序:J→I、G→I和A→H;一般学习路径一:4个逆序:I→F、J→F、D→G和A→H;一般学习路径二:3个逆序:I→F、J→F和D→G;推测关系路线:1个逆序:I→J;知识基学习路线一:2个逆序G→I和A→H;路线二:3个逆序:J→I、D→G和A→H;路线三:3个逆序:J→F、D→G和A→H;路线四:2个逆序:J→F和D→G。其次,以推测关系学习路线作为参考基准,答对率降序和关键学习路径有同1个逆序:I→J;个别学习路径0逆序;一般学习路径一和二有相同2个逆序:I→J、I→F;知识基路线一和二0逆序;三和四有同1个逆序:I→J。统计共29个逆序:7个I→J、5个A→H和D→G、4个I→F和J→F、2个G→I和J→I,分析原因:1. 作为基准的答对率和推测关系本身有一个逆序I→J或者J→I,I比较特殊无法严格划分难度级;2. IJ、AH、DG、IF、JF、GI之间本来就都没有推测关系,原因是两题考查内容没有逻辑关系难度却相似,比如,A是数据结构树加深度优先算法H是数学求逆元,AH考查内容不同,同理DG、FJ、GI和FI,所以出现以上逆序。因此有些题目难度很相似不容易区分,这些题目集中在中等难题及中等简单题之间。 除了一般学习路径,个别和关键路径均加入概率计算,从图4可得,概率效果更好,尤其是关键学习路径,与推测关系和答对率完全符合,采用关键学习路径研究ACM竞赛学习,这也与麦裕华[12]和何庆辉[13]在高中化学的氧化还原反应和离子反应的研究结果一致。麦认为知识空间理论提供的关键学习路径是基于学生知识和能力具体表现的量化建议,它可以在“补救”和“预防”这两方面产生作用,教师可以依据节点(题目)的出现顺序,依次对排列较后的节点进行补救教学,补救不是从学科知识的逻辑结构出发,而是从学生实际的认知需求出发,这更加适合学生的学习需求和产生预期的学习效果;在预防方面,教师备新课时参考关键学习路径,调整常规教学顺序和优化教学设计,从源头降低学习难度。何讨论了从两方面进行补救教学,一是根据关键学习路径优化教学设计,二是制作离子反应的系列微课供学生个性化自学,微课有助于解决教师教学目标定位和学生学习需求存在落差的教学矛盾;再者何也发现关键学习路径可为教师的新课备课提供参考。 ACM竞赛题型只有编程题,每一道题都是一个实际应用问题,要求每支队伍三位选手互相配合在五个小时内综合运用所学知识分析和解决问题,编写并提交可运行程序。这体现ACM竞赛理念,重点考察知识的综合运用和编程能力。难点在于知识的运用和编程能力的培养,为了攻克难点,大部分高校都有自己的ACM竞赛平台——Online Judge,简称OJ。OJ是ACM竞赛的在线评判网站,第一次使用需注册账号和密码,然后用自己熟悉的语言(Python/Pascal/C/C++/Java)写好源代码提交,网站实时自动返回判别结果:正确通过AC(Accepted)或者错误返回,常见错误:编译错(Compilation Error)、答案错WA(Wrong Answer)、格式错PE(Presentation Error)、超时TLE(Time Limit Exceeded)等,只有AC才算做对一题。选手在第一时间知道答题结果,并根据网站提示信息进行程序的再次修改与提交。通常每个平台提供了成千上万道编程题,题目多且杂。选手一般选择几个平台来刷题,国内知名平台有北大POJ、浙大ZOJ、杭电HDU、计蒜客和牛客等,国外知名平台有俄罗斯的Ural州立大学(http:∥acm.timus.ru/)和俄罗斯萨拉托夫大学(https:∥codeforces.com/)。后来出现虚拟在线评判VJ(Virtual Judge,https:∥vjudge.net/https:∥vjudge.net/),VJ并非常规OJ平台,它通过爬取其他OJ网站题目,选手可以直接在VJ上查找并提交各种OJ网站的题目,然后将题目通过VJ账号在真正的OJ上提交并把结果返回,相当于OJ平台的中介,目前VJ网站已经包含了35个OJ平台,选手使用VJ较为普遍。 从表4可知竞赛题关键学习路径上每题对应的答对率、难度和具体知识点(详见附录)。ACM竞赛题目涵盖了程序设计语言、数据结构、算法、数学四门学科的理论知识和方法,更重要的是将这四门学科的知识融合在一起分析和解决问题。首先,采用本案的技术对更多历年赛题查寻关键学习路径,从易到难解析具体知识点及其相关应用题目,通过关键学习路径结合选手的等级和积分(后面介绍)从易到难地推送适合选手个人水平的题目,即先AC简单题才能做难题,循序渐进地培养选手从计算机角度思考和解决问题的能力,这是参考ALEKS网站。其次,AC每一道题根据题目难度奖励积分,每做完一个专题升一级并按积分兑换奖品,奖品是进阶的学习资料包括模拟比赛、测试数据、解题分析、视频、微课和标准解答程序等,类似游戏机制激发选手做题兴趣,改变传统评价机制,选手通过等级和积分了解个人实力。游戏之所以吸引人,一个重要原因就是它能够激发人战胜困难的勇气,越是有挑战,挑战的难度越大,就越能激发勇者的斗志[20]。总之,关键学习路径结合OJ平台的创新使得选手不依赖教练的提醒和监督,完全能对自己的训练现状进行准确的分析和评价,并进一步培养选手的做题兴趣、挑战勇气和实战能力。 关键学习路径与OJ线上平台充分结合。首先,统计选手们在OJ平台的历史竞赛和平时训练数据,从AC题型和数量两个维度对选手知识水平特征进行向量化描述,评估选手水平并进行等级划分;然后,根据选手群体的竞赛成绩构建学习空间;而后,采用贪心算法MaxPath从学习路径中挖掘出关键学习路径,并推送合适难度等级题给相应等级的选手,为其平时训练提供个性化支持服务,关键学习路径可有效提升选手的训练效率、竞赛成绩和训练满意度,有利于选手对知识的主动建构、内化及迁移,仅靠个人的精力与智慧难以找到关键学习路径;最后,在OJ平台上设置奖励积分和升级激励引发选手做题兴趣,像玩游戏一样地训练。该方法可以从爆炸式增长的繁复的学习资源和活动中生成简洁、精准的个性化学习路径,既能有效解决选手的学习迷航与认知过载问题,还能促进学习资源的高效利用。知识空间理论的发展为学习路径的实现提供了理论指引和技术支撑,使每位选手获得最适合自己知识水平的学习资料,从而实现精准训练。然而对双方结合还处在探索阶段,对于如何结合双方以获得更高效训练效果,仍要从更多细节进一步研究和实践。 提出学习空间理论在ACM竞赛的应用框架和技术路线,主要有三个方面:(1)竞赛解题情况转换为形式背景,答对为1,答错为0,得到二维数据表。(2)由(1)得到所有学生知识状态,加上ø和Q构成知识结构,知识结构并封闭形成知识空间,最后根据公设张成学习空间。(3)在(2)得到的学习空间上应用贪心算法MaxPath查寻学习路径,应用关键路径结合OJ平台激发选手做题兴趣和挑战勇气。未来工作继续学习空间理论在ACM的应用,结合关键学习路径与OJ平台以获得更好的训练效果,进一步完善技术细节以及改进算法。 致谢 胡祥恩教授指导搭建R语言平台,配置运行KST程序环境,下载所需要的程序包。胡教授作出重要贡献,特致谢忱。 附录 问题B:Math数学(解析:图上随机游走的模型、概率动态规划法) Avin向客户出售机器人,在第二个0时,Avin拿着机器人位于数字轴位置(0,0),他想和机器人一起去(L,0),他每秒走一单位距离,并且只能停在整数坐标,现在他决定遵循以下步行规则直到他和机器人一起到达(L,0):(1)如果Avin随身携带机器人,则机器人可能会以概率p掉落。(2)如果Avin丢下了机器人,他将以q的概率捡起它,如果Avin到达(L,0)没有机器人,他将立即转身。(3)如果Avin的机器人没有掉落,则向右走一步;不然他就往左走直到他和机器人在同一位置。现在求Avin和机器人到达(L,0)所需步行时间的期望? 问题C:Trap陷阱(解析:数论互质、容斥原理、暴力法) Avin正在研究等腰梯形,等腰梯形是凸四边形有两条相对平行的线,两条等长的腰和正面积。在这个问题中,我们要进一步求两个腰不平行(就是标准等腰梯形)。给定n条线,请你找出等腰梯形的数量,这些等腰梯形都要满足:他们的4条边长度的最大公约数是1。两个全等等腰梯形仅计数一次。 问题D:Wave波浪(解析:基础数据结构线性表、暴力法)Avin正在研究系列(series),如果满足以下条件则一个系列称为“Wave”:(1)它至少包含两个元素;(2)奇数位置的所有元素都相同;(3)偶数位置的所有元素都相同;(4)奇数位置的元素与偶数位置的元素不同。你得到的序列长度为n,Avin请你找到最长“Wave”子系列,子系列是系列的子序列。 问题E:Packing包装(解析:高级算法动态规划法)Avin的仓库有一条带m个出口的包装线,总共有n种货物都不在包装线上,第i个货物将在时间ti发送到xi出口,Avin每秒可以从一个出口发送最多一个货物到包装线。对于出口i,有一个关联的缓冲区大小为ai,货物可以放在缓冲区中。但是,在每秒结束时,如果出口的货物数量b大于ai,Avin必须支付使用费b-ai。由于Avin想省钱,他请你找到一个方案,以最低的使用费将所有货物发送到包装线。为了完成今天的工作,Avin必须将所有货物送至包装线,在时间ti到达的货物可以立即在ti时刻送到包装线上。 问题F:String字符串(解析:乘法原理)Avin有一个字符串,他想从中均匀随机地选择四个字符(允许选择重复的字符),请你计算出四个字符为“avin”的概率(顺序不可颠倒)。 问题G:Traffic交通(解析:基础数据结构线性表、暴力法)Avin在十字路口观察汽车,他发现有n辆汽车在东西方向上行驶,第i辆汽车在ai时刻通过交叉路口,南北方向也有m辆车在跑,第i辆汽车在时刻bi经过交叉路口,如果两辆车同时经过交叉路口,将会发生交通事故,为了实现世界爱与和平,所有在南北方向的车都会等待相同的一段时间,使得任何一辆车都不会发生相撞,请问最短的等待时间。 问题H:Rng随机数发生器(解析:数学线性求逆元)Avin正在研究如何分析数据,给定一个整数n,他使用以下公式来构造一个区间:首先随机等概率地生成一个介于1和n(含1和n)之间的整数r,然后均匀地生成另一个介于1和r(含1和r)之间的整数l,这样就构造出了一个区间[l,r]。Avin使用上述方法构造了两个区间,他问你两个区间相交的概率是多少?你应该输出p·(q^(-1))(MOD1,000,000,007)(如果你不知道这意味着什么,请百度逆元),而p/q表示这两个区间相交的概率。 问题I:Budget预算(解析:最低位决定答案)Avin的公司有许多正在进行的项目且预算不同,他公司的预算四舍五入到小数点后三位。但是,该公司正在更新系统,所有预算都会四舍五入到小数点后两位,例如,1.004将四舍五入至1.00,而1.995将四舍五入至2.00,Avin想知道由更新引起总预算的差值。 问题J:Worker工人(解析:按比例分配)Avin今天遇到一位有钱客户,如果Avin能解决一个难题,他将获得一百万美元。现在有n个仓库和m个工人,第i个仓库中的任何工人每天都可以处理ai个订单,客户想知道是否存在一种方案满足每个仓库都处理相同数量的订单,请注意每个工人都要被分配到仓库,没有工人可以偷懒。 问题K:Class上课 (解析:基础程序题解方程)Avin有两个数a和b,给出x=a+b,y=a-b,你能计算出a×b吗?3 实验结果与讨论
3.1 学习路线与学习路径比较
3.2 三种竞赛学习路径与答对率比较
3.3 OJ平台介绍
3.4 关键学习路径结合OJ平台创新评价机制激发做题兴趣
3.5 效果分析
4 结论与讨论

