Multi-scale Set-valued Information System and Its Optimal Scale Selection

CHEN Yan,HU Jun,ZHANG Qinghua,WANG Guoyin

(Chongqing Key Laboratory of Computational Intelligence,Chongqing University of Posts and Telecommunications，Chongqing 400065, China)

Abstract：The multi-scale information system is often studied as a special information system. The existing researches only discuss the information system that each object only takes a single value at all scales of an attribute. However, in some real-world data sets, the attribute value of an object is not limited to a single-value, but may take multiple values, namely a set-value. We propose the concept of multi-scale set-valued information system. The rough approximation at different scales and its related properties can be obtained via the similarity relation between objects in a multi-scale set-valued information system. In addition, the definition of optimal scale is proposed based on the generalized decision, upper approximation distribution, lower approximation distribution, and positive region in a multi-scale set-valued decision system. The relationships among these optimal scales based on different criterions are further analyzed from the perspectives of consistency and inconsistency.

Key words： multi-scale set-value information system; rough approximation;similarity relation; optimal scale

0 Introduction

Multi-scale analysis has been widely applied in many fields[1-4]. In a multi-scale information system, the data is represented on multiple levels of scale and has the information granule transformation process from the fine to the coarse scale. The optimal scale selection is a significant issue in multi-scale information systems. Wu and Leung discussed optimal scale selection and rule acquisition problems in multi-scale decision systems based on the classical rough sets and dual probabilistic rough sets[5-6]. From the perspective of consistency of decision systems, Xuetal.[7]and Wuetal.[8]respectively characterized optimal scale selections of consistent and inconsistent multi-scale decision systems by the belief and plausibility functions in the Dempster-Shafer theory of evidence. Considering the change of information systems, Chenetal.[9]studied the optimal scale selection of dynamic multi-scale decision systems when adding/deleting objects by using three-way decision. These studies are based on the assumptions that all attributes have the same scale level, and the selection of optimal scale is at the same scale. For different attributes have different levels of scale, Lietal.[10]introduced generalized multi-scale decision systems and proposed two new methods about the optimal scale combination in generalized multi-scale decision systems, and then proposed a stepwise optimal scale selection method that can effectively reduce time loss[11]. Then, Wu and Leung[12]discussed the relationship between several optimal scale combinations in generalized multi-scale decision systems. Luoetal.[13]studied three decision updating problems based on multi-scale information systems.

The present studies only consider that each object takes a single value at all scales of an attribute in multi-scale information systems. However, it may happen that some of the attributes have multiple values for an object. For example, when we evaluate the language ability of a student, the value under this attribute is a set-value because the student can speak several languages. In recent years, there are many researches about knowledge discovery and attribute reduction of set-valued information systems[14-19]. However, none of these studies have studied set-valued information systems from a multi-scale perspective. As the example mentioned above, if several groups of experts are asked to assess students from different stan-dards, then the results can be regarded as evaluating students’ language ability from different scale. In addition, the attribute value of it may be a set value. To address this kind of problem, the multi-scale set-valued information system is firstly proposed and the selection of the optimal scale of a multi-scale set-valued information system is discussed in this paper.

Some basic concepts of multi-scale information systems are introduced. In Section 1, the definition of multi-scale set-valued information system is proposed and the related concepts are introduced. Then we propose four functions of a multi-scale set-valued decision system and discuss their relationship among different scales in Section 2. Section 3 investigates the selection of optimal scale in multi-scale set-valued decision systems based on different constraint functions and discuss the relationship between them from the perspective of consistency and inconsistency. Finally, we summarize the paper and outlook the further research in Section 4.

1 Preliminaries

This section reviews some basic concepts of Pawlak’s rough set[20]and multi-scale information systems[5,21].

1.1 Pawlak’s rough set

Definition1[20]Let (U,R) be a Pawlak approximate space andXbe an arbitrary subset ofU. Then one can characterizeXby a pair of upper and lower approximations which are defined as follows:

The accuracy ofXin (U,R) is defined as follows:

Where |·| indicates the cardinality of the set. Clearly,0≤αR(X)≤1. IfXis definable, thenαR(X)=1.

1.2 Multi-scale information systems

Multi-scale information system is a kind of system where objects can take different values under an attribute according to different measurement scales. In this section we review some basic concepts of multi-scale information systems.

Definition3[6]LetUbe a nonempty set, andψ1,ψ2be two partitions ofU. For eachφ1∈ψ1, if there existsφ2∈ψ2such thatφ1⊆φ2, then we say thatψ1is finer thanψ2orψ2is coarser thanψ1, and is denoted asψ1⊆ψ2.

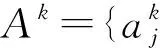
RA1⊆RA2⊆…⊆RAI,

ForX⊆U, a nested sequence of rough set approximations ofXcan be obtained:

Hence, a sequence of accuracies ofXunder different scales can be obtained:

αAI(X)≤αAI-1(X)≤…≤αA2(X)≤αA1(X).

It shows that the finer scale, the higher approximation accuracy ofX.

2 Multi-scale set-valued information systems

In some practical problems, an object may take multiple values at some scales of an attribute. To address this kind of problem, we propose the concept of multi-scale set-valued information systems in this section.

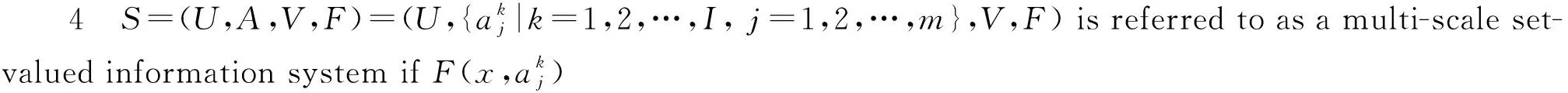
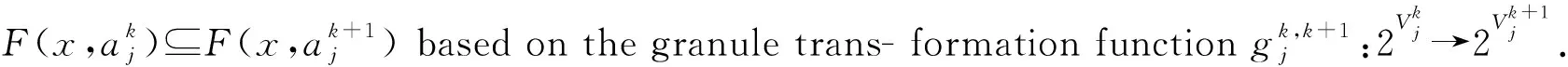
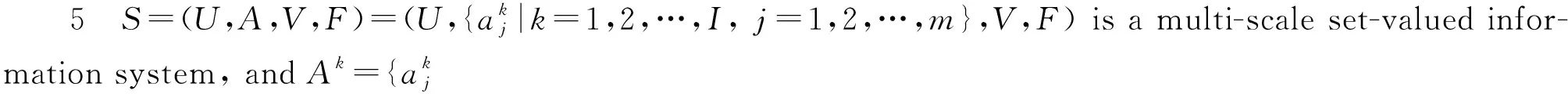
∀a∈Ak}.

it shows the relationship about similarity relations under different scales, and we can obtain that the coarser the scale is, the coarser covering ofUis.

Moreover, the accuracy of rough set approximation is defined as follow:

Therefore, a sequence of accuracies ofXat different scales can be obtained:

That is, the finer the scale is, the higher approximation accuracy ofXis inS.

3 Multi-scale set-valued decision systems

Decision system is a special information system which has both conditional and decision attri-bute. Here are some basic concepts and definitions about a multi-scale set-valued decision system.

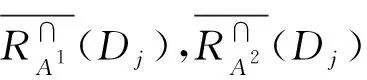
HA1(d)⊆HA2(d)⊆…⊆HAI-1(d)⊆HAI(d)

LAI(d)⊆LAI-1(d)⊆…⊆LA2(d)⊆LA1(d)

POSAI(d)⊆POSAI-1(d)⊆…

⊆POSA2(d)⊆POSA1(d).

It indicated that as the scale becomes coarser, the upper approximation distribution becomes finer, the lower approximation distribution becomes finer, and the positive domain becomes smaller.

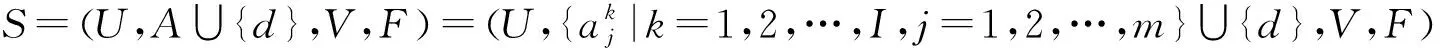
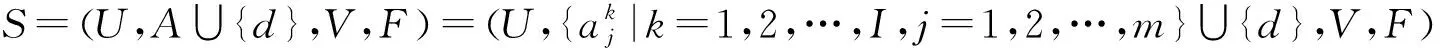
∂A1(x)⊆∂A2(x)⊆…⊆∂AI-1(x)⊆∂AI(x).

It shows that the coarser the scale is, the larger the generalized decision value ofxis.

Example1 Table 1 is an example of a multi-scale set-valued decision systemS=(U,A,V,F), whereU={x1,x2,…,x10},A={a1,a2,a3}. The system has three levels of scale, so it can be decomposed into three single-scale set-valued decision systems. We can calculate at the first level of scaleS1(as shown in Table 2):

Meanwhile, at the 2nd level of scaleS2(as shown in Table 3):

At the 3rd level of scale S3(as shown in Table 4):

LetX={x2,x3,x8,x9}, then

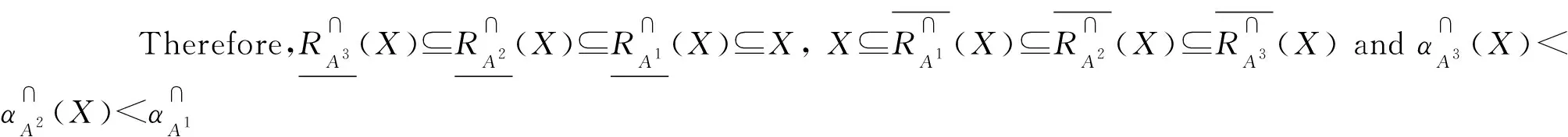
4 Optimal scale selection in multi-scale set-valued decision systems

It can be found from the above discussion that the approximation accuracy is the highest at the finest scale in a multi-scale set-valued decision system. However, the finer scale of data means the higher cost. Thus, it is a main issue to select the optimal scale such that the objective result obtained at that scale is consistent with the finest scale and the cost is relatively lower. Next, we give several optimal scale definitions based on different criterions.

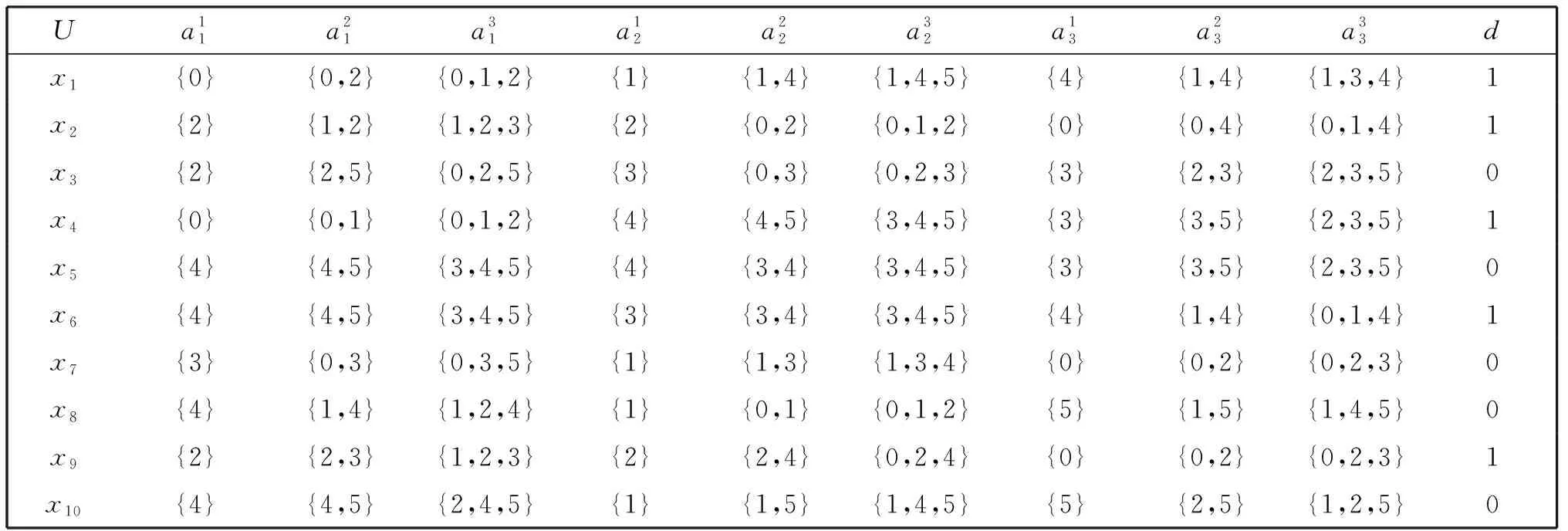
Table 1 A multi-scale set-valued decision system S

Table 2 The 1st scale set-valued decision system S1

Table 3 The 2nd scale set-valued decision system S2

Table 4 The 3rd scale set-valued decision system S3

(1)MAk(x)=MA1(x),

(2)MAk+1(x)≠MA1(x).

whereMAkis a kind of constraint function in a multi-scale set-valued decision system. The definition means that the objective result at thekth scale is consistent with the finest scale, and the objective result at thek+1 th scale is inconsistent with the finest scale. Namely,kis optimal scale ofSif and only if it is the coarsest scale in which the result of the constraint functionMAkinSkis consistent with the finest scaleS1.

The constraint functionMAkcan be the generalized decision function ∂Ak, upper approximation distribution functionHAk, lower approximation distribution functionLAk, or positive region functionPOSAk. Meanwhile,kis called the generalized decision optimal scalek∂, upper approximate optimal scalekH, lower approximate optimal scalekL, and positive region optimal scalekP.

Next, the relationship between these optimal scales mentioned above are discussed in consistent and inconsistent multi-scale set-valued decision systems.

4.1 Optimal scale selection in consistent multi-scale set-valued decision systems

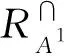
k∂=kH=kL=kP.

That is, the generalized decision optimal scale, the upper approximate optimal scale, the lower approximate optimal scale, and the positive region optimal scale are the same in a consistent multi-scale set-valued decision system.

From the similarity class calculated by example 1, at the 1st scaleS1(as shown in Table 2):

∂A1(x1)=∂A1(x2)=∂A1(x4)=

∂A1(x6)=∂A1(x9)={1}

∂A1(x3)=∂A1(x5)=∂A1(x7)=

∂A1(x8)=∂A1(x10)={0},

HA1(d)=LA1(d)=({x1,x2,x4,x6,x9},

{x3,x5,x7,x8,x10}),POSA1(d)=U.

At the 2nd scaleS2(as shown in Table 3):

∂A2(x1)=∂A2(x2)=∂A2(x4)=

∂A2(x6)=∂A2(x9)={1}

∂A2(x3)=∂A2(x5)=∂A2(x7)=

∂A2(x8)=∂A2(x10)={0}

HA2(d)=LA2(d)=({x1,x2,x4,x6,x9},

{x3,x5,x7,x8,x10}),

POSA2(d)=U.

At the 3rd scaleS3(as shown in Table 4):

∂A3(xi)={1,2},i=1,2,…,10.

HA3(d)=(U,U),LA3(d)=(ø,ø),POSA3(d)=ø.

4.2 Optimal scale selection in inconsistent multi-scale set-valued decision systems

In an inconsistent multi-scale set-valued decision systemS, it can be observed that the finest scale set-valued decision systemS1is inconsistent, we cannot get the maximum scale which keeps the classification or decision making consistent withSor obtain the equivalence relation with other optimal scales as above. However, there is still a correlation between the generalized decision optimal scalek∂, the upper approximate optimal scalekH, the lower approximate optimal scalekL, and the positive domain optimal scalekP.

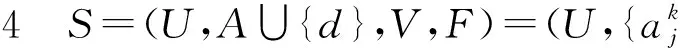
k∂=kH≤kL=kP.

It shows that the generalized decision optimal scale is the same with the upper approximate optimal scale; the lower approximate optimal scale is the same with the positive domain optimal scale, and the former is not more than the latter.

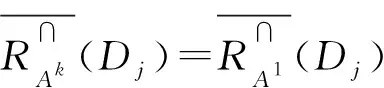
It shows that ifSkis upper approximate distribution consistent toS1then it must be lower approximation distribution consistent toS1. More-over, ifk1is the upper approximation optimal scale ofSandk2is the lower approximation optimal scale ofSthenk1≤k2, alternatively, the lower approximation optimal scale ofSis, in general, not less than the upper approximation optimal scale ofS. It can be proved by example 3.

(3)kL=kP: The conclusions can be directly proved by the definition of the lower approximation distribution and the positive domain.

Example3 Table 5 is an example of an inconsistent multi-scale set-valued decision systemS, which have two attributes and each attribute has two scales.

Table 5 An inconsistent multi-scale set-valued decision system S

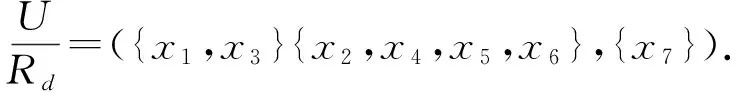
At the 1st scaleS1:

∂A1(x1)=∂A1(x7)={0,2},

∂A1(x2)=∂A1(x4)={1},

∂A1(x3)=∂A1(x5)=∂A1(x6)={0,1},

then, we haveHA1(d)=({x1,x3,x5,x6,x7},{x2,x3,x4,x5,x6},{x1,x7})LA1(d)=(ø,{x2,x4},ø),POSA1(d)={x2,x4}.

At the 2nd scaleS2:

∂A2(x1)={0,1,2},∂A2(x2)=∂A2(x4)={1},

∂A2(x3)=∂A2(x5)=∂A2(x6)={0,1},

∂A2(x7)={0,2},

then, we haveHA2(d)=({x1,x3,x5,x6,x7},{x1,x2,x3,x4,x5,x6},{x1,x7}),LA2(d)=(ø,{x2,x4},ø),POSA2(d)={x2,x4}.

Through analysis, ∃x∈Usuch that ∂A2(x)≠∂A1(x); and for all decision class we haveHA2(d)≠HA1(d),LA2(d)=LA1(d),POSA2(d)=POSA1(d). So,k=1 is the generalized decision optimal scale, the upper approximate optimal scale, andk=2 is the lower approximate optimal scale and the positive domain optimal scale of the inconsistent multi-scale set-valued decision systemS.

5 Conclusions

In this paper, we introduce the concept of multi-scale set-value information systems. Then, we defined different optimal scales based on different criteria. In a consistent multi-scale set-valued decision system, these optimal scales are equivalent; in an inconsistent multi-scale set-valued decision system, the generalized decision and upper approximate optimal scale are always not more than the lower approximate and positive domain optimal scale. In the paper, we only study multi-scale set-valued information systems in the context of conjunctive semantics.For further study, the multi-scale set-valued information system in the context of disjunctive semantics will be studied. And the current work is only based on theory which assumed that all attributes have the same scale, we will further consider the generalized multi-scale set-valued information system with different scales for different attributes and applying them to practical problems