P 波和SV 波耦合入射饱和软土动力特性试验研究
2021-01-08赵瑞斌李瑞源刘中宪徐志涛
赵瑞斌,李瑞源,刘中宪,c,徐志涛
(天津城建大学a.土木工程学院;b.天津软土特性与工程环境重点实验室;c.土木建筑结构防护与加固重点实验室,天津300384)
地震引起的土体软化、变形、破坏以及震陷一直是土动力学研究的重点问题.随着实验仪器的发展,越来越多的学者开始采用实验来模拟地震荷载作用下土体的动强度、动孔压、动模量以及软化系数等.
目前,大多数模拟地震的土动力学实验采用Seed等[1-2]将地震荷载简化为垂直向上的剪切波,通过在试样上施加等效的正弦波来模拟地震荷载作用在土体中的动力特性.但大量地震实测数据表明,近场地震中地震波将不在垂直入射,而以一定的角度倾斜入射.比如,Takahiro 等[3]根据发生在日本东京的24 个近场强震记录,反演分析得出地震波在近地表的入射角度为12.4°~54.1°.尤红兵等[4]研究了水平层状场地在斜入射地震波作用下的动力响应,得出大多数实际地震波的入射角度为30°左右,采用垂直入射时计算结果可能偏于不安全.
以往大多数地震波的模拟主要是以横(S、SV)波为研究对象,鲜有考虑P 波的影响.这是由于P 波在远场地震中衰减很快,在地表产生动力特性微小.但是,随着近年来全球地震频发,城市直下型地震发生时,其产生的P 波在地表的作用不容忽略.例如,对2008 年四川汶川地震的研究[5-6]表明,地表建筑物的破坏是纵波和横波共同作用的结果,P 波在近地表的波速可达5.35 km/s.Rascol[7]通过实验研究表明P 波和S波耦合能够显著加快孔隙水压力的提升,导致砂土液化.谷川[8]通过变围压动三轴设备采用循环剪应力和循环正应力耦合来模拟P 波和S 波耦合对饱和软黏土动力特性的影响,发现在特定情况下土体的强度明显降低,传统seed 方法高估了土体的动强度,但实验并未考虑入射角度和耦合相位差的影响.同时由于城市直下型地震带来的经济损失不可估量,因此研究P波与SV 波耦合入射时,入射角和耦合相位差对土体动力特性的影响十分重要.
基于此,本文利用GCTS 空心圆柱扭剪仪[9]开展了不同入射角和相位差下P 波与SV 波耦合入射饱和软土的动力特性试验.研究了不同入射角和相位差下应力路径的区别与联系,获得了不同试验条件下的滞回曲线、广义剪应变、孔压变化规律,并建立动孔压的增长模型,为P 波与SV 波耦合入射滨海软土的土体动力特性提供科学依据.
1 试样制备及试验土样
1.1 试验土样

表1 天津滨海试验用土物理力学指标
1.2 试样制备及受力状态
利用切土器先将整个土样削成高200 mm,直径100 mm 的圆柱试样,然后将圆柱试样置于护筒中,在内径切土器上将土样切取成内径50 mm 空心圆柱试样,如图1 所示.

图1 空心圆柱土样
土样试验时受力状态如图2 所示,W、MT、Pi、P0为地震荷载作用于土体的力,其在试样上产生的应力结果如图3 所示.轴向应力σz,径向应力σr,环向应力σθ,扭剪应力τzθ,在理论分析过程中,将平面应力状态下的水平向作用力等效为空心圆柱试样的环向应力,即σx=σθ;剪应力等效为切向正应力,即τxy=τzθ.
1.3 饱和与固结条件
饱和:采用反压饱和.将削好的空心圆柱试样装样于空心圆柱扭剪仪反压饱和系统,进行饱和试验[10].试验饱和参数设置为:最终围压为120 kpa;反压为100 kpa;时间设置为30 min;检测B 值时围压增量为30 kpa;当B 值达到0.97 时认为饱和完成.
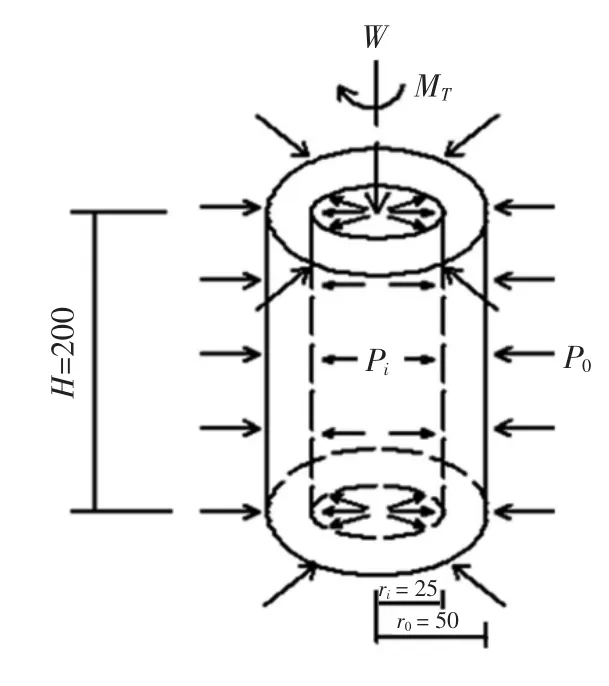
图2 空心圆柱样受力状态

图3 空心圆柱试样薄壁单元体受力状态
固结:本次试验,用GCTS 系统中的固有模块进行k0固结.其设定方法为通过控制反压控制器吸/排水的体积,使其等于试样的体应变,最终达到k0固结状态.最终试样竖向有效固结应力为120 kpa.固结过程中土样1 h 排水量不超过0.1 cm3,即可视为固结完成.
2 试验方案
根据地震波在半无限弹性空间中的传播理论[11-12]得知,P 波在传播过程中主要引起土体正应力变化,SV 波在传播过程中导致土体的剪应力变化. 因此,P波和SV 波耦合入射会导致土体正应力和剪应力同时变化,如图4 所示.在实际地震中,SV 波总是滞后于P波,通过考虑P 波和SV 波的相位差来模拟SV 波的滞后性.

图4 地震波引起的应力场
以P 波和SV 波频率相同(1 Hz)为条件,通过MATLAB 编程对相同的入射角的P 波和SV 波单独作用在饱和软土中动力特性求解,得到各自的围压应力、扭转应力和轴向应力,再采用矢量叠加得到施加在空心圆柱试样上的荷载,而矢量叠加的夹角即为相位差.通过GCTS 系统输入应力峰值、频率进行试验获得土体的应力、应变和孔压等数据.表2 为施加在空心圆柱试样上的应力.

表2 基于理论计算施加在空心圆柱试样上的应力
3 试验结果及分析
3.1 应力路径
当地震波频率为1 Hz 时,不同试验方案的应力路径如图5 所示.
我根本不知道私奔是什么意思,可李姐姐说,那是世上最美妙的一件事。我喜欢跟刘佳做美妙的事,我要和刘佳把世上美妙的事都做一遍。后来我爹妈和他爸妈一起找到了在田埂里睡得正香的我们,那是我头一次见我妈手里没拿着锅铲,她见了我,手掌拍拍地落在我身上,把我的迷糊劲都打没了,她边叫边哭,陈胖子,我倒底是欠了你什么哟,你个混帐东西!

图5 q-τ 应力路径
图5 中偏应力q=σ1-σ3.入射角为0°即垂直入射时(见图5a)相位差对应力路径的影响比较明显,相位差为0°和180°时应力路径为一条倾斜直线,相位差为45°、90°、135°的应力路径为椭圆. 入射角为15°时(见图5b),应力路径均为椭圆,相位差对应力路径的影响较小.入射角30°时(见图5c),相位差对应力路径影响较大,不同相位差的偏应力保持不变,但剪应力成倍增加,导致了土体的剪切破坏.整体上看,应力路径方向保持顺时针分向,与相位差和入射角度无关.
3.2 剪应力-剪应变发展模式
在地震荷载作用下土体循环软化、动强度降低的过程中,剪应力具有明显的作用效果.为探究不同入射角度和相位差耦合的P 波和SV 波对土体强度和循环软化的影响,绘制出全振动过程的剪应力-剪应变曲线,如图6-8 所示.由于篇幅所限,本文仅选取相位差为90°时不同入射角的滞回曲线,说明相位差对剪应力-剪应变曲线的影响.
引用Seed 等[13]提出的回弹模量概念,参考邓鹏[14]的研究对应于本文中的定义,即

式中:τcy为循环剪应力;γcy为循环剪应变即第N 次循环荷载作用产生的最大剪应变与最小剪应变差值.回弹模量表述的几何意义是滞回圈的斜率,当滞回圈的斜率随着振次增加而减小时,说明回弹模量也在逐渐减小,表明土体此时发生了循环软化现象[14].
从图8a、8b、8c 可以看出,入射角为15°时,循环加载下的滞回圈不封闭,加载初期,塑性累积较快发展,随振次的增加,滞回圈面积逐渐变大并左移,剪应变逐渐累积,破坏时最大剪应变约为10%;随着振次的增加,滞回圈的斜率逐渐减小,土体刚度逐渐减小,回弹模量越来越小,土体发生循环软化.
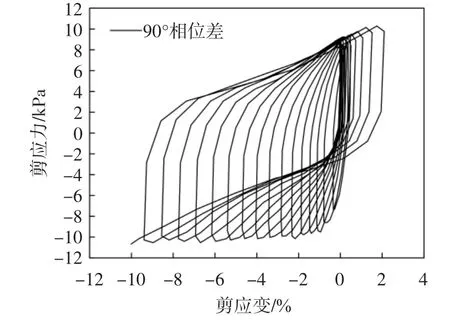
图6 0°入射角的滞回曲线

图7 30°入射角的滞回曲线

图8 15°入射角滞回曲线
对比研究图6、图7、图8b 可知,随着入射角的增加,滞回曲线斜率(即回弹模量)减小的速率在逐渐减小,土体软化现象减缓;在相同入射角下(见图8),不同相位差下的滞回曲线保持较好的一致性,表明相位差对滞回曲线影响较小.
3.3 广义剪应变发展模式
考虑到地震荷载作用下土体不仅产生剪应变,而且也有轴向应变的产生,为了更好地描述土体的变形情况,本文采用广义剪应变γg分析试验过程中的土体应变发展情况.参考郭莹[15]对广义剪应变γg的表达式,即

式中:ε1、ε2、ε3分别为单元体的大、中、小主应变.
不同方案的广义剪应变-振次曲线如图9 所示,由试验结果来看,广义剪应变曲线可以分为两种类型,稳定增长型和快速增长型.从图9a、图9b 可以看出,加载初期应变缓慢累积,当达到某一振次时广义应变开始迅速增加,直至强度完全丧失,此类应变发展类型为快速增长型.从图9c 可以看出广义剪应变随振次的增加先快速增长后缓慢增长最后趋于平缓,此类应变发展类型为稳定增长型.
在P 波与SV 波耦合入射时,地震波入射角对广义应变发展具有显著影响,地震波小角度入射时土体应变发展更为迅速,破坏振次更少.原因是地震波在小角度入射时,土体主要承受剪切荷载,土体的抗剪切能力较弱,故较早出现土体破坏.在同一入射角下,不同相位差下的剪应变遵循一定的规律:在相同振次下,随着相位差增大,广义剪应变先增大后减小,在90°相位差时广义剪应变达到最大值.以入射角15°为例,振次为25 次时,在耦合相位差为0°时为2.5%,耦合相位差为45°时为4.7%,耦合相位差为90°时最大,达到7%,耦合相位差为135°时为3.8%,耦合相位差为180°时为3%.
对比图9a、9b 和9c 可以看出,广义剪应变在耦合相位差为90°时累积最快,土体变形最大,对建筑结构的影响最严重.同时可以看出,在0°和15°入射下,土体的破坏振次为30 次左右,而在30°入射下,土体的破坏振次可达120 次.综上,入射角度对软土变形影响较大,小角度斜入射时土体动强度最小;其次相位差对软土变形有较大影响,地震波耦合相位差为90°时,土体应变发展相对迅速.
3.4 动孔压的应力模型
定义动荷载作用下饱和软土的孔压u 与平均有效固结应力σc′的比值为孔压比ru.图10 分别给出饱和软土在不同入射角度下P 波和SV 波耦合作用时孔压比ru与耦合相位差α、振次N 的曲线.

图9 不同入射角下不同相位差的广义剪应变

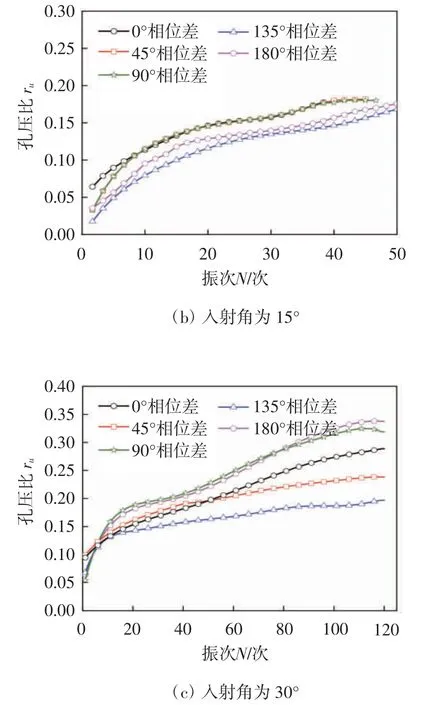
图10 不同入射角不同相位差下的孔压比-振次曲线
由图10a、10b 和10c 可以看出,入射角度为30°时,土体破坏的孔压比明显大于其他情况,同时破坏振次也明显增加.但在相同振次下,各种试验下的孔压比相差不大,这表明地震波入射角度对土体的孔隙水压力影响不大.可能是由于土层均取在软黏土层,而且试样高度仅为200 mm,其沉积时间相差不大,土体的各项异性不能充分展现.
整体上随着试验振次的增加,孔压比逐渐增大,直至最后土样破坏,但是其增长速率逐渐减小,最后趋于平缓.P 波和SV 波耦合相位差对孔压比ru的影响没有展现出特定的规律,但相位差为90°时土样破坏时的孔压比都相对较大,据试验的孔压发展规律,采用双参数的双曲线孔压发展模型[16-18]拟合孔压发展规律,即

式中:A、B 均为拟合参数(见表3-5).
根据相关系数R2可以看出双参数的双曲线模型可以很好地拟合软土在地震荷载作用下的孔压比-振次曲线.

表3 0°入射拟合结果
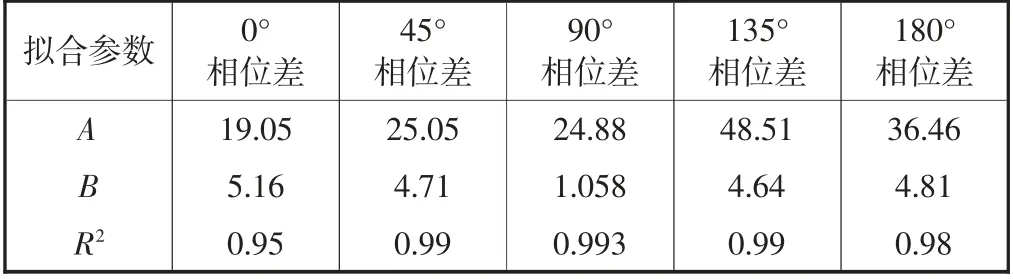
表4 15°入射拟合结果
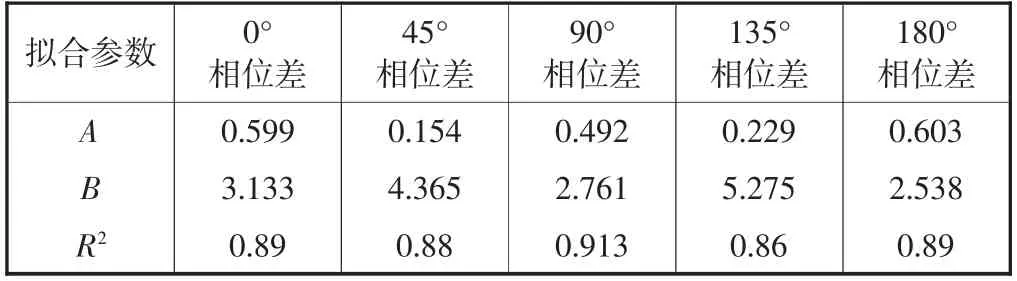
表5 30°入射拟合结果
4 结 论
针对天津滨海软土,利用空心圆柱扭剪仪开展了一系列四项耦合振动的不排水循环加载试验,研究了不同入射角不同相位差下耦合波(P 波和SV 耦合)对饱和软土的动力特性.主要结论如下.
(1)P 波和SV 波耦合入射时,地震波入射角度对土体变形具有明显的影响.随入射角度的增加,饱和软土的广义剪应变由“快速增长型”向“稳定增长型”转变,耦合相位差为90°时,土体的广义剪应变最大,土体变形最大;入射角为15°时滞回圈发展最快,土体软化明显.综合来看,15°入射角90°耦合相位差时,土体的变形最大,最容易发生破坏.
(2)当地震波入射角度一定时,耦合相位差对孔压比的影响并未遵循特定规律,但相位差为90°时,孔压的累积速度最快,土体最容易遭到破坏;其次天津滨海软土的孔压比-振次曲线符合双参数的双曲线模型.
