正交匹配追踪算法的迭代残差重建方法

付 敏, 王金平

正交匹配追踪算法的迭代残差重建方法

付 敏, 王金平*

（宁波大学 数学与统计学院, 浙江 宁波 315211）

正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法是一种重要的压缩感知重构算法. OMP算法在每次迭代中选择与当前残差最相关的原子. 针对每次迭代需要重新计算残差的问题, 本文考虑偶数次迭代下残差未知的情况. 首先, 研究了奇数次迭代的残差与下一次迭代的残差之间的关系, 得到了一种偶数次迭代时选择原子的标准. 然后, 引入一种回溯机制来处理前面所得的迭代结果, 这种机制通过剔除其中多余的原子来实现精确重建. 据此, 提出了可减少计算残差的改进型正交匹配追踪算法.

稀疏重构; OMP算法; 回溯

压缩感知(Compressed Sensing, CS)理论[1]作为一种新的信号采样理论突破了传统Nyquist采样定理的限制, 它充分利用信号的稀疏性, 将高维信号没有损失地压缩采样成低维信号, 最后通过重构算法精确或高概率地重建原始信号. CS理论主要涉及稀疏表示、测量矩阵、重构算法等3个核心方面. 其中, 重构算法是将CS理论推向实用化的关键之一. 目前, 重构算法主要分为3类: (1)基追踪算法, (2)贪婪算法, (3)组合算法. 这些算法中, 贪婪算法因其结构简单易实现的优势而得到了广泛应用. OMP算法[2]是一种常用的压缩感知贪婪算法. 以OMP算法为原型, 研究者们提出了很多改进算法, 例如对原子正则化的正则化正交匹配追踪(Regularized OMP, ROMP)算法[3], 使用回溯思想的压缩采样匹配追踪(Compressive Sampling MP, CoSaMP)算法[4]和子空间追踪(Subspace Pursuit, SP)算法[5], 采用门限阈值的分段正交匹配追踪(Stage- wise OMP, StOMP)算法[6], 还有稀疏度自适应的自适应匹配追踪(Sparsity Adaptive MP, SAMP)算法[7]以及利用统计学方法来进行迭代预测的迭代预测匹配追踪(Iterative Forecast OMP, IFOMP)算法[8]. 在前人研究的基础上, 本文对OMP算法加以改进, 得到相关结果.

1 预备知识

该解不惟一, 而CS理论: 如果一个信号是稀疏的, 那么就可以用具有约束等距性(Restricted Isometry Property, RIP)的测量矩阵来观测该信号, 然后通过求解一个优化问题就可重构原始信号[1].

由CS理论可知, 恢复稀疏信号即求解最优化问题:

OMP算法的基本思想是在每次迭代过程中, 选择与残差最相关的原子, 并将测量信号正交投影到已选原子集合生成的超平面上, 剩余部分作为新的残差, 继续迭代, 直到达到设置的迭代次数为止. OMP算法的阶模型为

正交匹配追踪算法过程如下.

循环执行各步骤:

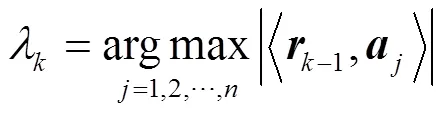
步骤3 由最小二乘得到

由步骤1, OMP算法原子选择标准是选择与残差内积绝对值最大的那个原子, 即

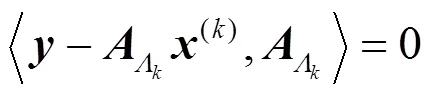
可得

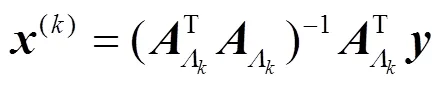
由结论2, 发现残差与前面已选的原子都是正交的, 这可避免重复选用原子.

2 主要结果

本节主要研究相邻两次迭代残差间的关系, 从而给出一种等价的原子选择标准, 迭代结束后, 加入一种回溯机制来处理迭代结果.

证明 (i)由定义1得

(ii)由定义1及内积定义得

(iii)由定义1得

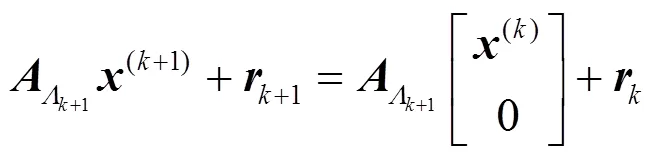
将矩阵分块得

宪法学研究要立足于新时代坚持和发展中国特色社会主义的伟大实践。积极回应社会发展中重大的宪法关切，更加注重原创性和本土性研究，把宪法学的宏大叙事与具象表达、研究的开放性与自主性结合起来。坚持中国特色社会主义的政治优势和制度优势，努力提炼并不断丰富发展具有中国特色和中国气派的宪法学理论体系、概念体系、话语体系，不断增强中国宪法学的解释力、传播力和影响力。

进一步地,

故有

将式(7)代入式(6), 得到

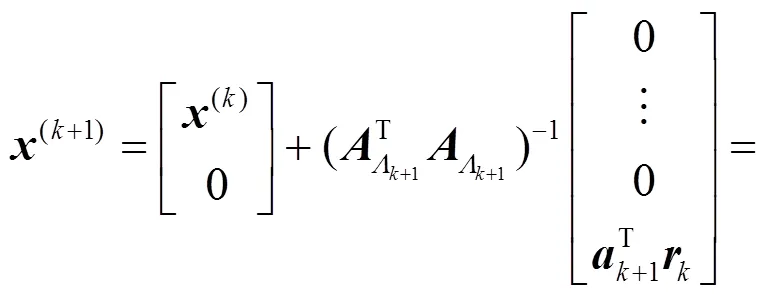
从而有

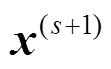
改进的正交匹配追踪算法如下.

3 总结

本文利用Cholesky迭代式分解, 得到OMP算法中相邻两次迭代残差间的关系, 可减少计算残差的次数. 迭代结束后, 通过引入回溯机制来对原子进行二次筛选, 从而实现精确重构.

[1] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4):1289-1306.

[2] Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12):4655- 4666.

[3] Needell D, Vershynin R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2):310-316.

[4] Needell D, Tropp J A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2009, 26(3):301-321.

[5] Dai W, Milenkovic O. Subspace pursuit for compressive sensing signal reconstruction[J]. IEEE Transactions on Information Theory, 2009, 55(5):2230-2249.

[6] Donoho D L, Tsaig Y, Drori I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2012, 58(2):1094-1121.

[7] Do T T, Gan L, Nguyen N, et al. Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]. Asilonar Conference on Signals, Systems, and Computers, 2008:581-587.

[8] 刘学文, 肖嵩, 王玲, 等. 迭代预测正交匹配追踪算法[J]. 信号处理, 2017, 33(2):178-184.

[9] Baraniuk R G. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4):118-121.

An iterative residual reconstruction method of the orthogonal matching pursuit algorithm

FU Min, WANG Jinping*

( school of Mathematics and Statistics, Ningbo University, Ningbo 315211, China )

Orthogonal Matching Pursuit (OMP) is an important compressed sensing reconstruction algorithm. The OMP algorithm selects the atoms which are most associated to the current residual in each iteration. For the problem of recalculating the residual in each iteration, we consider the case where the residual of even number iterations is unknown. First, we study the relationship between the residuals of odd number iterations and the residuals of the next iteration followed by obtaining a benchmark for selecting atoms in even number iterations. Then we introduce a backtracking mechanism to process the results of previous iterations. The mechanism achieves the precise reconstruction by removing the extra atoms. An improved orthogonal matching pursuit algorithm is thus presented in this study.

sparse reconstruction; OMP algorithm; backtracking

O177.92

A

1001-5132（2021）01-0050-05

2020−06−01.

宁波大学学报（理工版）网址: http://journallg.nbu.edu.cn/

国家自然科学基金（62071262）.

付敏（1997－）, 女, 安徽合肥人, 在读硕士研究生, 主要研究方向: 积分变换与图像处理. E-mail: 2818391447@qq.com

王金平（1962－）, 男, 湖北武汉人, 博士/教授, 主要研究方向: 积分变换与图像处理. E-mail: wangjinping@nbu.edu.cn

（责任编辑 韩 超）