环境约束下珠三角区域能源效率评价及演变趋势

赵敏 赵鑫

摘 要：坚持以能源绿色发展与清洁利用为导向，提高能源效率是促进珠三角区域绿色低碳循环发展的关键手段。选取珠三角区域9个现代都市2005～2018年的面板数据，使用规模报酬可变的超效率DEA模型和Malmquist生产率指数探寻环境资源约束下该区域全要素能源效率的特征差异与动静态演变趋势。研究表明，2005～2018年珠三角区域的TFEE水平小幅下降后稳步上升，平均TFEE值为0.89，仅深圳和珠海位于最优生产前面上，具有一定节能减排空间。平均TFPCH为0.12%，变动幅度很小，技术效率和技术进步的变动增长率分别为0.21%和0.76%，呈现出稳定波动趋势，表明两者均是能源效率增长的主要驱动因素。总体来讲，珠三角区域的能源效率水平较为稳定，但内部各城市间效率水平的差异较为明显，整体节能减排目标的实现仍有一定提升空间，因而在制定能源环境政策时要考虑因城制宜。

关键词：绿色发展;能源效率;珠三角区域;超效率DEA

中图分类号：F224;O242  文献标识码：A  文章编号：1673-260X（2021）12-0084-08

《新时代的中国能源发展》白皮书（2020）中将提高能源效率、促进节能减排、能源清洁低碳生产作为推动绿色发展的实现途径。我国在推动能源消耗方式變革的过程中，实行能源消费总量和能源强度的双控制度，按行政区域设定控制目标。作为中国改革先行区的珠三角区域，应率先在能源方面实施创新驱动战略，深化重点领域和关键产业的市场化改革，推动能源高质量发展，提升能源使用效率，加快构建清洁低碳、安全高效的新型能源体系，逐步推动区域能源结构转型和经济结构优化。

本文以环境约束下珠三角区域的能源效率评价及演变趋势分析为重点研究对象，以期为该区域提高能源效率和制定节能减排目标提供有价值的政策建议。

1 文献梳理与评述

能源效率的常见评价方法是全要素指标法，其中最具代表性的是参数法和非参数法。参数法中的随机前沿分析（Stochastic Frontier Analysis，简记SFA）方法使用频率较高，它是由Meeusen et al和Aigner et al共同提出的一种可以考虑随机因素影响的SFA模型，其优点是依据具体生产函数形式来考虑影响能源效率的有关变量[1，2];非参数法中最为常用且最具代表性的是数据包络分析（Data Envelopment Analysis，简记DEA），最初由Charnes和Cooper共同提出，通过生产过程中形成的线性规划模型来测算评价单元效率的非参数方法[3]。其优势在于无须提前假定生产函数形式，设定的“多投入-多产出”指标体系不受数据单位影响，可通过数学步骤确定各要素的权重关系，具有很强的客观性[4]。DEA方法规避了SFA方法强假设生产函数形式的偏误，在效率评价中得到了研究学者更为广泛的认可[5-7]。

Chung et al在测算造纸业生产率时首次提出环境规制行为模型（AAM），将包含环境因素的非合意产出纳入生产过程中进行考量，使用方向性距离函数定义Malmquist-Luenberger指数法[8]，从而自由设定产出增加或污染减小的合意方向，使环境污染物的实际测度变为现实。吴军选用M-L法时将环境因素加入产出指标体系之中，测算我国1998～2007年工业全要素能源效率，结果表明技术进步对各省份工业TFP的增长起到关键作用[9]。Wu et al使用一种新型共享输入的两阶段DEA模型对包含环境污染问题的中国工业阶段全要素能源效率和整体效率进行评价，进而比较能源消耗和污染处理两个阶段的优劣[7]。范秋芳等在产出指标中加入SO2排放量作为非合意产出，选用BC2模型和Malmquist指数法对中国四大区域的全要素能源效率进行评价，实证分析表明各地区必须结合自身实际发展情况制定同供给侧改革相适宜的能源政策[10]。高鹏等结合非竞争型投入产出模型和超效率SBM模型，研究了中国产业部门的全要素直接能源效率和全要素隐含能源效率及其节能潜力[11]。田泽等、孙策等、孟晓等分别使用共同前沿动态SBM模型、Malmquist指数法和超效率DEA模型对我国重要城市群落的能源效率进行全面分析和评价，并探寻能源效率低下的原因[12-14]。Rong et al和Wu et al分别使用超效率DEA和网格DEA对中国各省份的能源效率水平进行评价，并探寻能源效率低下的原因[15，16]。

综上所述，学者在能源效率评价方面的研究成果颇丰。从测算方法来看，多数文献仅采用静态或者动态方法来进行效率评价，动静态方法结合的研究较少;从研究目标来看，多数学者选择国家或省际层面展开研究，而对区域和城市等单元的研究较少。鉴于此，本文聚焦环境约束下珠三角区域的能源效率，一是从区域角度进行细化研究，避免了省份之间存在的客观条件差异，能更有针对性地进行能源效率评价;二是使用动静态结合的方式进行综合分析，弥补了以往仅从动态视角或静态视角评价效率的单一性;三是依据全要素生产框架，在投入要素固定时选取“三废数据”作为非合意产出，更好衡量生产过程对环境造成的污染因素影响。

2 研究方法与模型

在Hu和Wang首次对全要素能源效率的度量做出综合界定的基础上，将珠三角区域包含的广佛肇、深东惠、珠中江作为评价单元[17]，对全要素能源效率及其变化率进行实证分析。首先使用基于投入导向型的超效率DEA模型测算环境约束下珠三角区域9个现代都市2005～2018年的全要素能源效率值;然后在环境方向性距离函数的基础上，使用Malmquist生产率指数法测度能源效率变化率，并分解为技术进步增长率和技术效率增长率;最后从动静态两方面对能源效率进行评价，综合分析二者的演变趋势，为区域节能减排政策的制定提供实证建议。另外，由于规模报酬不变（CRS）假定适合厂商在最优规模状态下运行，考虑到现实情境受政府管制、市场约束和信息不完全等因素的制约，本文选取规模报酬可变（VRS）的超效率DEA模型。

2.1 超效率DEA方法

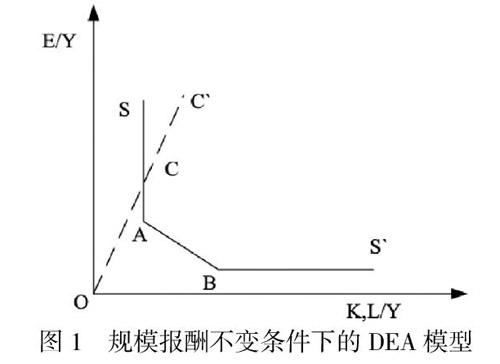
经典DEA模型在评价生产决策单元（DMU）的能源效率时，主要通过线性规划模型来判断DMU是否处于最优生产前沿面，从而对无效或低效的DMU进行效率测算。如图1所示，基于投入导向型的CRS-DEA模型，投入要素分别为能源（E）、资本（C）和劳力（L），且决策单元DMUA、DMUB和DMUC均处于数据包络线SS’上。Farrell建立的技术效率公式为θ=OC/OC’，当θ=1时，表明DMU技术有效且位于生产前沿面;若θ<1，则表明存在1-θ的效率损失[18]。例如，C’点位于包络线外且需要的投入比C点多，因此属于效率损失点，另外C点可以减少的能源投入量为CA（松弛变量），那么无效DMUC’实现最优效率的投入量为E=OC/CA=θOC’/CA。在全要素能源效率的分析框架中，测算每个DMU的效率值以及距离生产前沿面的能源投入调整量，可以表示实际投入的无效部分。因此，全要素能源效率（Total Factor Energy Efficiency，简记TFEE）通常定义为DMU实现最优效率时潜在（或理论、最佳）的能源投入与实际能源投入的比例关系，即TFEE=理论能源投入量/实际能源投入量。

上述经典DEA方法可能会出现多个DMU均位于同一生产前沿且相对有效的情形，从而无法对一系列相对有效的DMU进行后续的评价与比较。Andersen和Petersen建立的超效率DEA模型可以有效地解决这个难题[19]，通过运用DEA有效单元排序法便可对相对有效的DMU进行效率比较，具体做法是把目标评价DMU置于决策单元集合以外。如图2所示，投入导向型的超效率DEA模型，在测算DMUA的效率值时可以不必考虑整个决策单元集，A的数据包络线由原来的SABS’移动到SCBS’，此时A的效率值为θ=OA’/OA>1，其中无效率点C’的效率值和生产前沿面依旧不发生变化，可见超效率DEA模型使相对有效的评价单元的效率评价成为可能。

根据Fare et al提出的方向距离性函数（DDF）来构建珠三角区域的环境方向性产出函数，将环境约束因素加入能源效率分析框架，得到包含合意产出与非合意产出的生产性可能集[20]。Fare和Grosskopf对多个DMU投入产出的P（x）给出定义，指出其满足以下四点可处置性特性[21]：（1）投入要素的自由可处置;（2）产出项的弱可处置;（3）合意产出与非合意产出的联合生产性;（4）合意产出的强可处置。在超效率DEA模型框架下，假定k个决策单元（即城市）利用n种投入要素集xij=（x1k，x2k…xnk）∈RN，生产出m种合意产出集yrj=（y1k，y2k…ymk）∈RM与z种含环境污染物的非合意产出集ulj=（u1k，u2k…uzk）∈RZ，其环境生产可能性集合为：P（x）={（y，u;x→（y，u））}。若（y，u）∈P（x），且0<θ<1，则（θy，θu）∈P（x），表示投入固定时，两种产出的增减方向和比例相同，即u=0，y=0表示两种产出均为0。在输入输出指标确定的情况下，存在松弛变量时投入导向型超效率DEA模型的线性规划演变形式如下：

式（1）中θ表示全要素能源效率值，λj为决策单元的比例关系，松弛变量S-和S+分别代表投入过量或产出不足，ε为非阿基米德无穷小量，通常在计算中当作正无穷小进行处理。当θ*=1且S-=S+=0时表明该DMU0有效，同时能源效率最佳，即在产出不变时无法等比例减少整体或者部分投入量;当θ*=1且S-或S+不为零时，此时DMU0为弱有效，也可以说是由k个决策单元构成的生产系统中，产出固定情况下可以对投入向量实行结构性调整，此时的生产规模不是最优规模;当θ*<1且S-和S+两者均不为零或某项不为零的情况下，决策单元DMU0为非DEA有效，即在同等产出条件下存在投入过多的现象，可以对投入量加以调整和改进以达到最优。在（1）中加入条件Σλj=1即为规模报酬可变模型，因此，将评价DMU0排除在生产可能性集合外的超效率DEA线性规划形式可描述如下：

2.2 Malmquist指数法

Malmquist指数法对分析DMU位于不同时期的动态能源效率变化提供了极大便利。假定投入要素x自由可处置且规模报酬可变，用Malmquist生产率指数继续考察包含环境因素的能源效率变化率及其分解值。Paul et al改进生产率分析法并建立测算跨期生产率变化的Malmquist指数，通过计算距离函数（DF）的比率来衡量能源效率，进而评价两个时期DMU的动态生产率变化[22]。相对于Tomqvist指数和Fisher指数，Malmquist指数可以将能源效率变化分解为技术进步变化与技术效率变化[23]，公式中不包含价格信息可避免信息不对称产生的影响，此外多元指标体系无须假设其他条件。基于不同时期技术水平的Malmquist指数模型定义式为：

式（3）中M0代表生产过程中的投入产出矩阵，xt、yt、xt+1、yt+1分别为第t期和t+1期的投入量产出量，Dt和Dt+1表示以不同时期技术水平衡量的方向性距离函数。全要素能源效率变化率（TFPCH）可分解为规模报酬可变条件下的技术效率变化（EFFCH）和技术进步变化（TECH），另外EFFCH可二次分解为规模效率变化（SECH）与纯技术效率变化（PECH），同理（3）式可进一步表述为：

M0=TFPCH=TECH×EFFCH

=TECH×SECH×PECH  （4）

在统计学概念中，上述三个指标均为环比发展指数。当M0>1时，DMU的TFPCH呈现出增长趋势，TFEE较前期有所增加;当M0<1时，DMU的TFPCH呈现出降低趨势，TFEE较之前有所减少。其中EFFCH代表每个评价单元从时期t到t+1距离生产可能性前沿面的远近程度，指数值大于或小于1分别表示跨期的技术效率提高或降低;TECH代表每个评价单元从时期t到t+1在生产可能性前沿面上的移动情况，指数值大于或小于1分别表示跨期的技术进步或退步;PECH表示规模报酬可变时的技术效率变化情况;SECH表示规模经济对能源效率变化率的影响大小，可见TFPCH中不同指标的效率变化是决定M0提高或降低的根本原因。另外，需明确TFEE和TFPCH测量方法的区别之处，TFEE考察生产过程中某一固定期的DMU与最优生产前沿面的相对位置关系，隶属于静态分析范畴;而TFPCH通过测度DMU距最优生产前沿面的距离远近关系来表示技术效率变化，抑或是通过测度最优生产前沿面的位置变动关系来衡量技术进步变化，隶属于动态分析范畴[24]。

3 数据收集与变量说明

本文的研究范围为2005～2018年度珠三角区域9个现代都市的面板数据。结合参考文献的理论基础与方法模型，假定生产过程中的投入要素为资本、劳动力和能源三项，合意产出为生产总值，非合意产出为环境污染排放物。

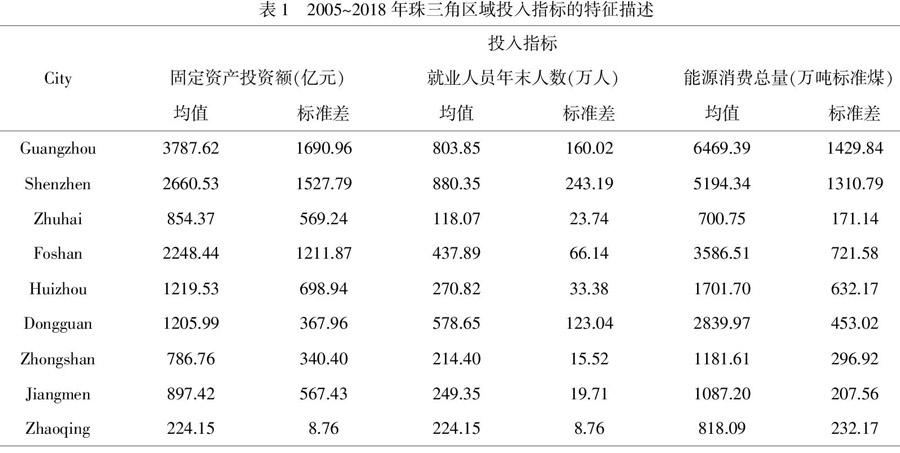
（1）资本。参照吴军的数据处理方法[9]，将各市的固定资产投资额（亿元）作为资本投入指标，根据2005年不变价格进行折算。

（2）劳动力。劳动人员的素质与劳动消耗时间是衡量劳动投入的关键指标，鉴于数据的难获取性，使用各市历年的就业人员年末人数（万人）作为劳动投入指标。

（3）能源。通常做法是将评价单元的全部能源消耗数量作为能源投入。鉴于不同城市所消耗的能源种类有差别，可以将石油、天然气、电力、煤炭等主要资源的消耗量统一转换加总为新单位“吨标准煤”，另外，还应包括部分煤炭资源使用时有二次转换的消耗量。为保证各变量统计口径的统一性，将各市的单位GDP能耗系数统一换算为能源消耗总量（万吨标准煤），使用能源消耗总量表示能源投入指标。

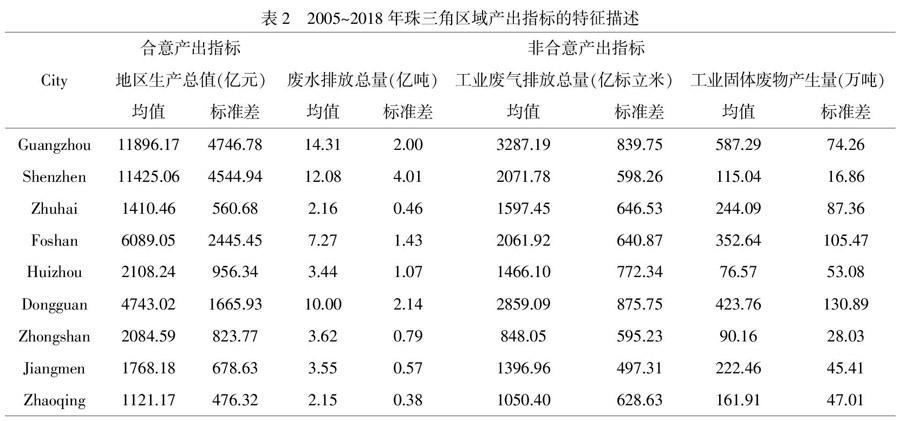
（4）合意产出。李双杰等在构建效率测算的指标体系时指出，为保持投入与产出的一致性并符合实际生产过程，若投入指标选取资本和劳动力，则产出指标应选择增加值;若投入指标选择资本、劳动力和中间投入，则产出指标应选择总产值[4]。文章使用以2005年不变价格计的实际地区生产总值（亿元）为合意产出。

（5）非合意产出。国内外学者对非合意产出的选择中涵盖了众多污染物种类[24]，由于能源在实际消耗中产生的污染物会直接影响大气和水质，因此使用工业“三废”排放量来表示非合意产出。广东省在2013年起不再提供工业固体废物排放量数据，鉴于统计口径的改变，现选用工业固体废物产生量进行替代，其中2005年部分城市的固废产生量缺失数据采用线性插补法补齐。综上，选取废水排放总量（亿吨）、工业废气排放总量（亿标立米）与工业固体废物产生量（万吨）的“三废”指标为非合意产出。

以上投入产出指标数据均来源于历年的《广东统计年鉴》，其描述性统计如表1和表2所示。

4 能源效率结果实证分析

根据珠三角区域的投入产出面板数据，运用投入导向的VRS超效率DEA方法，固定资本额、劳动力和能源消耗量作为投入要素，合意产出与非合意产出共同作为产出要素，使用MaxDEA7.1软件测算环境约束下各城市的TFEE和TFPCH及其分解值变化情况，全面分析各都市能源效率的变动规律和本质特征。

4.1 环境约束下的全要素能源效率

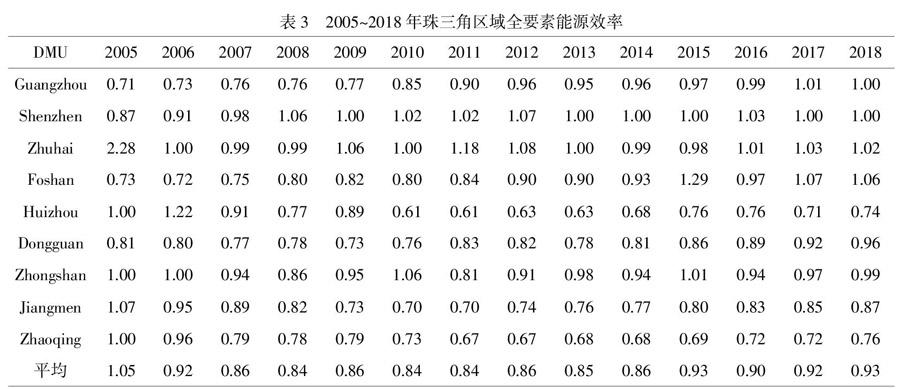
珠三角区域9个现代都市2005～2018年的TFEE结果见表3。

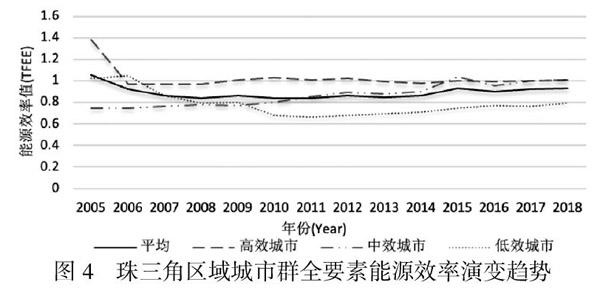
从经济区域角度来看，珠三角区域2005～2018年的TFEE的变动规律特征为：（1）整体来看，14年的平均值为0.89，表明该地区尚存在11%的节能潜力;（2）在能源效率的演变趋势方面，2005～2018年珠三角经济区的TFEE从2006～2008年出现小幅度下降后一直处于平稳状态，2009～2014年间能源效率始终在0.84-0.86间稳定波动，这与叶祥松等得出的能源效率在2000～2013间有所提升不相符[25]，究其原因可能是其评价指标体系中未包括非合意产出。2015年后能源效率出现明显上升趋势，除2016年外其余年份的效率值均大于0.92，表明珠三角经济区实行“腾笼换鸟”的产业升级政策有效，转移或淘汰高耗能产业使得能源效率有所提升。此外，加快经济结构调整也是效率提升原因之一。

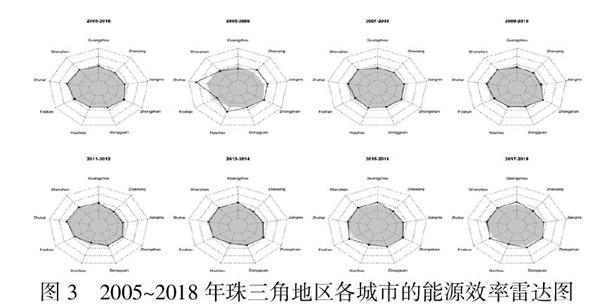
从城市层面来看，珠三角区域的9个城市在2005～2018年间的TFEE存在显著差异，如图3所示，雷达图可直观对比出各城市间相近两年的TFEE变化。其主要演变特征：（1）珠三角区域仅有个别城市的平均TFEE在评价年份达到有效生产前沿面水平，其中深圳和珠海在若干年份处于有效前沿面上，属于相对有效的城市，珠海的TFEE最高，2005～2018年的平均值达到1.12;深圳次之，14年来的TFEE均值为1。能源效率最低的城市依次为肇庆和惠州，14年平均值仅为0.76和0.78。（2）在TFEE的演变趋势方面，TFEE呈现出“稳态收敛”趋势的城市有深圳、珠海和中山，这些城市的城市化水平始终处于珠三角前列;呈现出“螺旋稳步上升”趋势的城市有广州、佛山和东莞，表明产业升级和结构调整逐步趋于完善;表现为“先降低后上升”趋势的城市有惠州、肇庆和江门，这些城市的重工业产业占比依旧较高，根据TFEE演变趋势可将上述城市分为“高、中、低”三个层次，效率值变化如图4所示。（3）城市间的TFEE变化幅度明显，处于有效生产前沿面的城市从2005年的5个变为2018年的4个，但区域整体能源效率水平有显著提高，处于中间水平城市的效率值在0.80～0.95之间波动，具备一定的节能潜力和效率提升空间。综上所述，珠三角经济区的节能减排应注重不在有效前沿面的城市，尤其是应重点关注惠州市、肇庆市、江门市三个低效率城市，需加强城市领域相关能源政策的有效落实，加大对科技创新和人才培养的支持力度，推动低能耗、低质量产业结构优化升级。

4.2 Malmquist能源效率增长率指数

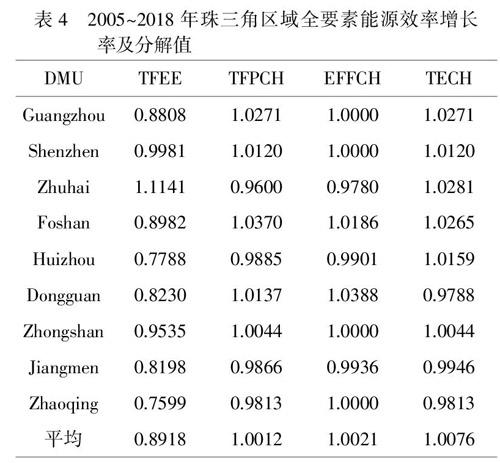
Malmquist能源效率增长率指数的测算结果详见表4。注意此处测算的TFPCH是动态变化趋势，可二次分解为技术效率变化（EFFCH）与技术进步变化（TECH）。

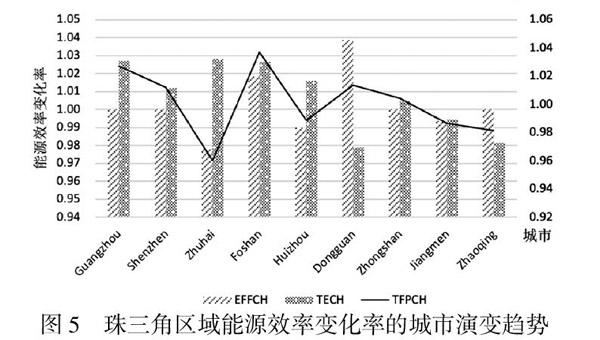
珠三角区域各城市的TFPCH演变趋势如下：（1）TFPCH呈现出曲折上升趋势，变化幅度从2006年的-4.81%上升到2018年的1.72%;EFFCH先上升后下降，從2006年-5.81%最高升至2015年的10.96%，然后降至2018年的-2.17%;TECH较为平稳，除2017年的值为7.58%外，其余年份始终在5%范围内上下波动，无显著增长趋势。（2）2006～2018年间三者的平均增长率均≥1，在TFPCH较为稳定的情况下，技术效率改善和生产技术进步处于一种此消彼长的状态，但二者均对TFPCH的提升做出贡献，其中技术效率对2015年的整体增长率升高起关键作用，技术进步对2017～2018年整体增长率提升有强推动作用。（3）EFFCH和TECH的平均变化率差异较小，除个别年间出现显著升高（2015、2017年）或降低（2006、2007年）的情况外，二者皆可反映为TFEE提升的主要驱动要素。

图5很好地反映了珠三角区域城市群TFPCH及其分解值的贡献比重和演变趋势，在文章的测算时间范围内，TFPCH提升幅度较为平稳，表明该区域能源消耗方式相对合理、污染物排放监管长期有效，能源政策实施、新技术引进和产业升级起到良性循环促进作用。技术进步和技术效率的推动作用不一，珠海、深圳等高效城市的技术进步贡献大于技术效率，有着更强的推动作用，肇庆、江门等低效城市的分解值始终处于低水平，推动作用较弱，需要得到重点关注，也可为情况类似的其他地区提供参照借鉴，以便寻求实现可持续发展的可行路径。

5 结论性研究建议

本文从环境约束视角出发，在非合意产出中引入的“三废”排放量拓宽了产出指标体系，使用投入导向的超效率DEA模型考察了珠三角区域2005～2018年的静态TFEE，同时利用Malmquist指数测算动态TFPCH及其分解值，分析各城市能效差异和演变趋势，得到一些现有研究之下的新结论。第一，从整体角度来看。考虑环境约束下珠三角区域的TFEE呈现出先降低后升高的趋势，说明该区域实施的节能减排政策对提升能效水平有效。TFPCH变化起伏不一，总体上呈现小幅下降的收敛趋势，技术进步和技术效率均为能源效率改善做出重要贡献，是区域绿色发展的主要驱动因素;第二，从各城市层面来看。城市间TFEE差异较为显著，没有城市在14年来一直处于有效前沿面上，除深圳和珠海外，其余城市具有不同程度的节能空间，两个分解值的贡献水平和作用大小因城市而异。

提高能源效率，缩小城市差距，应考虑城市定位、产业结构等客观条件，是珠三角区域在经济新常态下能源发展过程中的重点关注问题。文章从区域视角出发，有针对性地提出以下几点建议。

实证性研究建议如下。首先，应根据城市间TFEE水平差异，考虑优化城市间资源配置，加强产业互助合作，强化国际先进技术水平交流，结合多种因素达到提高能源效率、优化产业结构，打造区域城市群的比较优势与核心竞争力，以期趋同并超越国际高水平区域发展模式。其次，对于深圳、中山和佛山三个高效城市，需继续实施能源创新驱动战略，发展新能源行业，关注市场化改革等重点领域，探寻能源效率提升的新途径，建设清洁高效的能源消耗体系;对于佛山、广州、东莞三个中效城市，需要进一步优化要素投入比例、加大技术进步和技术效率方面的资金注入、提高要素利用率和边际产出率等;对于江门、惠州和肇庆三个低效城市，应该以提升TFEE为核心，转变以往的高消耗和粗放发展模式，逐步取消产能落后行业，大力发展服务业等，共同促进城市能源和产业结构转型。最后，技术进步和技术效率皆是珠三角区域TFPCH提升的主要动力，尤其是2016年以来，珠三角地区的技术效率贡献率很小甚至为负值，应该注重投入要素结构和生产技术的优化配置，力求实现技术进步和技术效率的同步促进提升，最终打造区域经济高质量发展、节能减排效果显著提高的共赢局面。

参考文献：

〔1〕W. Meeusen and J. Broeck. Technical efficiency and dimension of the firm： Some results on the use of frontier production functions[J]. Empirical Economics， 1977， 2（02）： 109-122.

〔2〕Aigner Dennis and Lovell C.A.Knox and Schmidt Peter. Formulation and estimation of stochastic frontier production function models[J]. 1977， 6（01）： 21-37.

〔3〕Charnes A. and Cooper W.W. and Rhodes E.. Measuring the efficiency of decision making units[J].1978， 2（06）： 429-444.

〔4〕李雙杰，李春琦.全要素能源效率测度方法的修正设计与应用[J].数量经济技术经济研究，2018， 35（09）：110-125.

〔5〕Malin Song et al. Environmental efficiency and economic growth of China： A Ray slack-based model analysis[J]. European Journal of Operational Research， 2018， 269（01）： 51-63.

〔6〕Toshiyuki Sueyoshi and Yan Yuan and Mika Goto. A literature study for DEA applied to energy and environment[J]. Energy Economics， 2017， 62： 104-124.

〔7〕Jie Wu et al. Total-factor energy efficiency evaluation of Chinese industry by using two-stage DEA model with shared inputs[J]. Annals of Operations Research， 2017， 255（1-2）： 257-276.

〔8〕Y.H. Chung and R. F？re and S. Grosskopf. Productivity and Undesirable Outputs： A Directional Distance Function Approach[J]. Journal of Environmental Management， 1997， 51（03）： 229-240.

〔9〕吴军.环境约束下中国地区工业全要素生产率增长及收敛分析[J].数量经济技术经济研究，2009， 26（11）：17-27.

〔10〕范秋芳，王丽洋.中国全要素能源效率及区域差异研究——基于BCC和Malmquist模型[J].工业技术经济，2018，37（12）：61-69.

〔11〕高鹏，岳书敬.中国产业部门全要素隐含能源效率的测度研究[J].数量经济技术经济研究，2020， 37（11）：61-80.

〔12〕田泽，张怀婧，任芳容.环境约束下中国三大城市群能源效率评价与影响因素比较研究[J].软科学，2020，34（12）：87-95.

〔13〕孙策，成金华，孙莉.长江中游地区能源效率评价研究：与京津冀、长三角和珠三角地区的比较[J].中国矿业，2017，26（08）：69-74+111.

〔14〕孟晓，孔群喜，汪丽娟.新型工业化视角下“双三角”都市圈的工业能源效率差异——基于超效率DEA方法的实证研究[J].资源科学，2013，35（06）：1202-1210.

〔15〕Wang Rong and Wang Qizhen and Yao Shuangliang. Evaluation and difference analysis of regional energy efficiency in China under the carbon neutrality targets： Insights from DEA and Theil models[J]. Journal of Environmental Management， 2021， 293.

〔16〕Geng Wu et al. Using a network DEA model to assess the energy efficiency of regions in China[J]. IOP Conference Series： Earth and Environmental Science， 2020， 546（02）： 022054.

〔17〕Hu J. ，Wang S.， Total Factor Energy Efficiency of regions in China[J]. Energy Policy， 2006， 34（17）： 3206-3217.

〔18〕Farrell M. J.. The Measurement of Productive Efficiency[J]. Journal of the Royal Statistical Society. Series A （General）， 1957， 120（03）： 253-290.

〔19〕Per Andersen and Niels Christian Petersen. A Procedure for Ranking Efficient Units in Data Envelopment Analysis[J]. Management Science， 1993， 39（10）： 1261-1264.

〔20〕R. Fare and S. Grosskopf and Jr. Pasueka. Environmental Production Functions and Environmental Directional Distance Functions[J]. Energy， 2007， 32， 1055-1066.

〔21〕Rolf Fare and Shawna Grosskopf and Dimitris Margaritis. Advances In Data Envelopment Analysis[M]. SG Singapore： World Scientific Publishing Company， 2015.

〔22〕Paul W. Bauer. Decomposing TFP growth in the presence of cost inefficiency， nonconstant returns to scale， and technological progress[J]. Journal of Productivity Analysis， 1990， 1（04）： 287-299.

〔23〕馬海良，黄德春，姚惠泽.中国三大经济区域全要素能源效率研究——基于超效率DEA模型和Malmquist指数[J].中国人口·资源与环境，2011，21（11）：38-43.

〔24〕王兵，吴延瑞，颜鹏飞.中国区域环境效率与环境全要素生产率增长[J].经济研究，2010，45（05）：95-109.

〔25〕叶祥松，刘敬，王江波.经济增长质量与能源效率研究——以珠三角地区为例[J].江西财经大学学报，2017，19（05）：3-13.