Multiple of Solutions for a Class of KirchhoffType Problems

LI Guofa(李国发)

(College of Mathematics and Statistics，Qujing Normal University，Qujing 655011，China)

Abstract: In this paper，we study the existence of multiple of solutions for a class of Kirchhofftype problems with 4-superlinear nonlinearity via the minimax methods.An example is given to verify the main results.

Key words: Kirchhofftype problem; Multiple of solution; Mountain pass theorem;Superlinear nonlinearity

1.Introduction and Main Results

In this paper，we concern the existence of nontrivial solutions for the following Kirchhofftype problem

where Ω ⊂RN(N =1，2，3)is a bounded domain with smooth boundary ∂Ω，and a，b are two positive constants and f :R →R is continuous.

In the past several decades，the Kirchhofftype problems like (1.1) have been studied in bounded domain or whole space RNvia variational methods.XIE，et al.[1-6]obtained the nontrivial solutions or nodal(sign-changing)solutions of Kirchhofftype problem(1.1)with the nonlinearity f(t) is asymptotically 4-linear at infinity.When f(t) is 4-superlinear at infinity，SUN and TANG，et al.[7-9]have studied the existence of nontrivial solutions sign-changing solutions and infinitely many large energy solutions for (1.1).

Moreover，HE and ZOU[10]have obtained a sequence of a.e.positive weak solutions tending to zero in L∞(Ω)for(1.1).ZHANG and Perera[11]have obtained the positive，negative and sign-changing solution for (1.1) when f(t) is 4-sublinear，asymptotically 4-linear，or 4-superlinear.CHEN and OU[12]have studied the existence of sign-changing and nontrivial solutions for (1.1) when f(t)=αt+βt3，where α，β ∈R are two real parameters.

Note that，for the case f(t) is superlinear，the authors have considered the following variant Ambrosetti-Rabinowitz(short as AR)condition to get the boundedness of the Palais-Smale (short as PS) sequence

µF(t)≤tf(t)，µ＞4，∀t ∈R，

(H1) f(t)=o(|t|) uniformly as |t|→0;

(H2) There exists a positive constant C such that |f(t)| ≤C(1+|t|p-1) for all t ∈R，where 2 ＜p ＜2*when N =3，and 2 ＜p ＜+∞when N =1，2;

(H4) 0 ＜4F(t)≤tf(t) for all t ∈R，where

(H5) f(t)=-f(-t) for all t ∈R.

RemarkThere are many functions satisfying (H1) to (H5).For example，f(t) =t3ln(1+t2)，t ∈R.

Now，we state our main results as follows:

Theorem 1.1Assume that f(t) satisfies (H1)-(H4).Then the problem (1.1) has one nontrivial solution.

Theorem 1.2Assume that f(t)satisfies(H1)-(H5).Then the problem(1.1)has infinity many nontrivial solutions.

The methods of this paper are the minimax principles which are established in [13].Moreover，we need some techniques which are studied in [14].First，we give the mountain pass geometry of the energy functional of the problem (1.1) and prove the (PS)csequence satisfies PS condition in Section 2.Second，we prove our main results by mountain pass theorem and symmetric mountain pass theorem in Section 3.Throughout this paper，we will denote the following notations: ‖u‖p(1 ＜p ≤∞) is the norm in Lp(Ω); →and ⇀denote strong and weak convergence，respectively;〈·，·〉denotes the duality pairing between a Banach space and its dual space; on(1) denotes on(1) →0 as n →∞and BRdenotes a ball with radius R ＞0.

2.Variational Setting and Preliminaries

Set

with the inner product 〈u，v〉=Ω∇u∇vdx and the norm

We observe that the energy functional J :X →R corresponding to (1.1) is given by

Clearly，critical points of J are the weak solutions of (1.1).Now，we state some lemmas.

Lemma 2.1The functional J satisfies (PS)ccondition.

ProofLet{un}⊂X be any(PS)csequence of J，i.e.J(un)=c+on(1)and J′(un)→0 in X-1，where X-1is the dual space of X.First，we prove {un} is bounded in X and {un}has strong convergence subsequence.By (H4)，we have

4c+1+on(1)‖un‖≥4J(un)-〈J′(un)，un〉

which shows that {un} is bounded.

Since {un} is bounded in X，up to a subsequence of {un}，denoted as {un}，there exists u ∈X such that un⇀u in X，un→u in Lp(Ω) and un(x) →u(x) a.e.x ∈Ω.Then，we know

Moreover，we mention that

From the conditions (H1) and (H2)，for each ε ＞0 there exists a constant Cε＞0 such that

Then，by the previous convergence and the arbitrariness of ε，we have

By (2.1) and (2.3)，we have

Hence，

Then ‖un-u‖2→0，as n →∞，that is，un→u in X.This completes the proof.

Lemma 2.2Assume that(H1)-(H4)hold.Then there exist β，ρ ＞0 such that J(u)≥β for all ‖u‖=ρ.

ProofIt deduces from (2.2) and (H3) that

Since Ω is a bounded domain，it deduces from the embedding XLp(Ω) that there exist constants γp＞0 such that

Setting Sρ={u ∈X :‖u‖=ρ}，and choosing ε ＞0，by (2.4) and (2.5)，we have

Lemma 2.3Assume that (H1)-(H4) hold.Then there exists e ∈such that J(e)≤0.

ProofFor given nonzero functionchoose M ＞0 such thatBy (H3)，there exists constant C ＞0 such that F(t)≥M|t|4-C for all t ∈R.Then，we obtain

It follows that J(tφ)≤0 as t →+∞.Hence，let e=tφ，we have J(e)≤0 for large t ＞0.

3.Proof of Main Results

Proof of Theorem 1.1By Lemmas 2.1-2.3 and Theorem 2.2 in[13]，we get the results.

Proof of Theorem 1.2Since XL2(Ω) and L2(Ω) is a separable Hilbert space，X has a countable orthogonal basis {ei}，i = 1，2，···.Let Vk= span{e1，e2，··· ，ek} and Ek=then X =Vk⊕Ek.Hence，by Lemma 2.2，we have

Indeed，for any finite dimensional subspace⊂X，there is a positive integral number k such that⊂Vk.Suppose to the contrary that there exists a sequence {un} such that{un}⊂⊂Vkand ‖un‖→∞as n →∞，but

Then

Set wn=un/‖un‖.Then，{wn}is bounded in X，up to a subsequence，we can assume that wn⇀w in X，wn→w in Lp(Ω)and wn(x)→w(x)a.e.x ∈Ω.Let Ω1={x ∈Ω :w(x)0}and Ω2={x ∈Ω :w(x)=0}.If meas(Ω1)＞0，by (H3) and Fatou’s Lemma，we have

which is a contradiction with (3.1).Hence，wn→0 in Lp(Ω).Since all norms are equivalent on the finite dimensional space，there exists a constant C ＞0 such that

Hence，

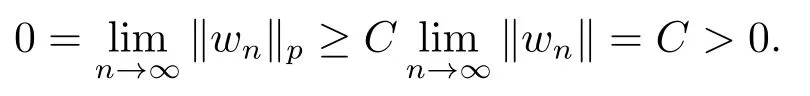
This is a contradiction and the desired conclusion is obtained.This means that there is a constant R=R()＞0 such that J ＜0 on.Moreover，by the conditions (H1) and(H5)，we know J(0) = 0 and J is even.Therefore，from Theorem 9.12 in [13]，we complete the proof.