带有线性记忆的波方程在Rn上的时间依赖吸引子

吴晓霞，马巧珍

( 西北师范大学数学与统计学院，甘肃 兰州730070)

1.引言

我们考虑如下带有线性记忆的波方程

时间依赖吸引子的存在性，其中u(x，t)是未知函数，h(·) ∈L2(Rn).η = ηt(x，s) := u(x，t)-u(x，t-s)，s ∈R+，ε(t)和f(u)分别满足下面的条件:

(F1) ε是单调递减的并满足:

特别地，存在L ＞0使得

(F2) 非线性项f ∈C1(R)，f(0)=0并满足

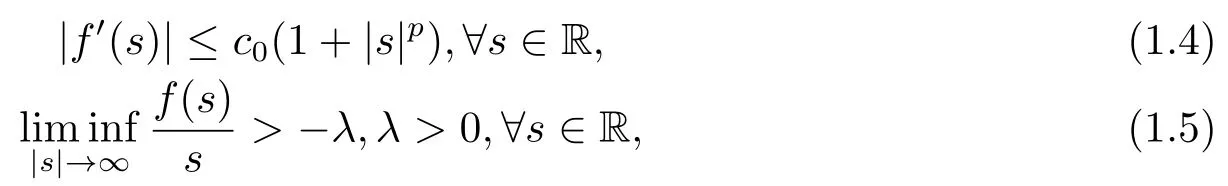
其中，当n=1，2时，0 ≤p ＜∞; 当n ≥3时，0 ≤p(n-2)≤2.

如文[1-3]，对ηt(x，s) = u(x，t)-u(x，t-s)两边分别关于t和s求导，计算后可将(1.1)化为下面的系统:

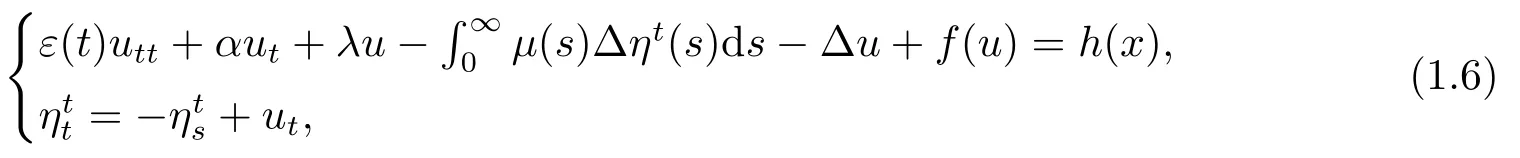
相应的初始条件为

其中

记忆核µ(·)满足以下条件:

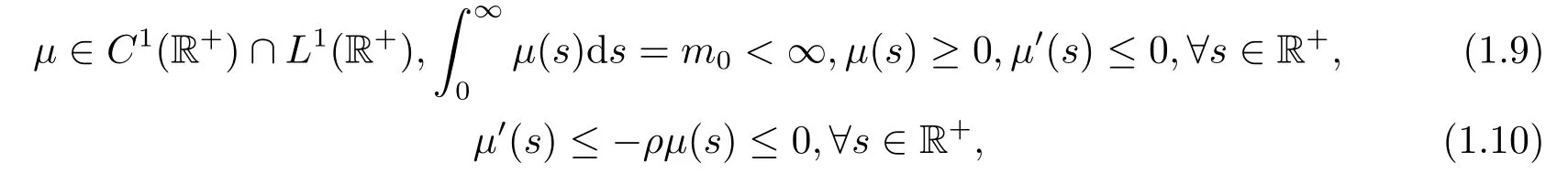
其中ρ是正常数.

方程(1.1)可以用来描述具有衰减记忆的粘弹性固体，其中耗散性由固体周围的介质，混合材料，相场以及波现象所体现，见文[4-6].

µ恒等于零时，方程(1.1)为阻尼波方程，这类问题已经被许多作者研究过.例如，当ε为常数时，文[7-12]在半群的框架下，利用全局吸引子的概念研究了解的长时间行为.而当ε依赖于时间且为正递减函数时，我们知道即使外力项不依赖于时间，系统(1.1)仍然为非自治的，其吸引子仍在非自治的框架下理解，见文[13-18].作者在文[19-20]中研究了有界域上带有非线性阻尼和线性记忆的波方程时间依赖吸引子的存在性，文[21-23]考虑了无界域上波方程解的长时间行为.无界域上plate方程时间依赖吸引子的存在性在文[24]中被研究.然而，时间依赖全空间Rn上带有线性记忆的波方程时间依赖吸引子的存在性目前还没有任何结果，因此我们在本文研究这一问题解的长时间行为.

2.准备知识

不失一般性，记H =L2(Rn)，内积和范数分别为〈·，·〉和‖·‖.对于s ∈R+，记Hs=Hs(Rn)=并赋予以下内积和范数:

特别地，

对于t ∈R，s ∈R+，有下面的时间依赖空间=Hs+1×Hs×(R+;Hs+1).

当s = 0时，记时间依赖空间为: Ht= H1×H ×(R+;H1)，对应的范数为:=

对∀t ∈R，设Xt是一族赋范线性空间，下面介绍Xt的R-球:

两集合(非空) B，C ⊂Xt的Hausdorff半距离表示为:

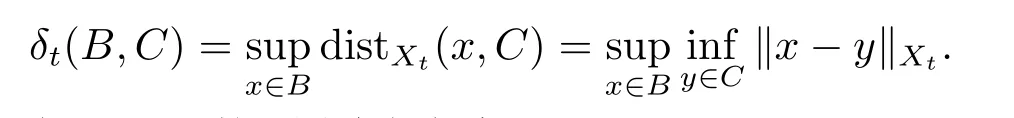
对于任意给定ϵ＞0，集合B ⊂Xt的ϵ-领域定义为

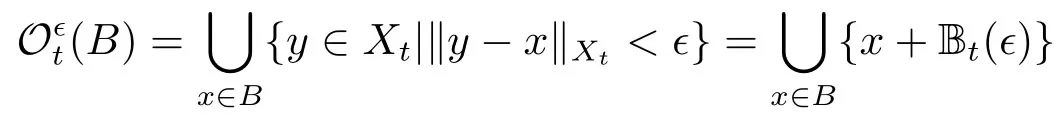
下面给出基本概念和抽象结果，详见文[13，18，24].

定义2.1设{Xt}t∈R是一族赋范线性空间.称双参数算子族{U(t，τ):Xτ→Xt，t ≥τ，τ ∈R}是一过程，如果它满足:

i) U(τ，τ)=Id是Xτ上的恒等映射，∀τ ∈R;

ii) U(t，s)U(s，τ)=U(t，τ)，∀t ≥s ≥τ.

定义2.2设有界集Ct⊂Xt，我们说集合族C = {Ct}t∈R是一致有界的，如果存在常数R ＞0，使得Ct⊂Bt(R)，∀t ∈R.

定义2.3一致有界集族B = {Bt}t∈R是过程U(t，τ)的时间依赖吸收集，如果对任意的R ＞0，存在常数t0，使得τ ≤t-t0⇒U(t，τ)Bτ(R)⊂Bt.

定义2.4一致有界族K={Kt}t∈R是拉回吸引的，若对所有ϵ＞0，族{(Kt)}t∈R是拉回吸收的.

定义2.5过程U(t，τ)的时间依赖吸引子是满足以下性质的最小的族U={At}t∈R:

i) 任意的At在Xt中是紧的;

ii) U是拉回吸引的，即对任意一致有界族C={Ct}t∈R，成立:

定理2.6[24]设{Xt}t∈R为一族Banach空间且C = {Ct}t∈R为{Xt}t∈R中的一致有界子集族.称定义在{Xt}t∈R×{Xt}t∈R上的函数，(·，·)为Ct×Ct上的渐近压缩函数是指:对任意t ∈R与任意序列⊂Ct，存在一个子序列使得:

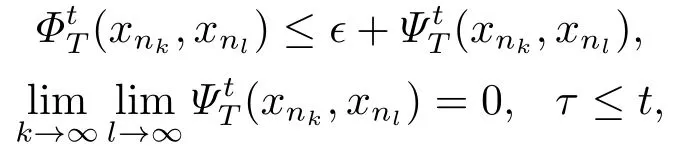
其中τ ≤t.我们用C(Ct)表示{Ct}t∈R×{Ct}t∈R上的渐近压缩函数全体.

定理2.7[24]设U(·，·)为{Xt}t∈R中的一族过程且对任意ϵ＞0，存在τ ＜T(ϵ) ≤t，∈C(CT)，使得对任意固定t ∈R，

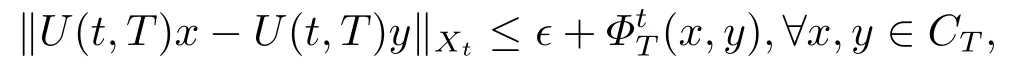
则U(·，·)是渐近压缩过程.

定理2.8[24]若过程U(·，·)是渐近压缩的，则它是拉回渐近紧的.

定理2.9[24]设U(·，·)是Banach空间族{Xt}t∈R中的过程，则{Xt}t∈R中U(·，·)有一个时间依赖全局吸引子U*={t∈R如果它满足下面的条件:

i) U(·，·)有拉回吸收族B={Bt}t∈R;

ii) U(·，·)是Bt上的拉回渐近压缩过程.

引理2.10[3]令F(u) =f(y)dy.根据(1.7)，取0 ＜ν = min{1，λ}，则存在ϱ(ν) ＞0，ci(ν)＞0(i=1，2)，使得

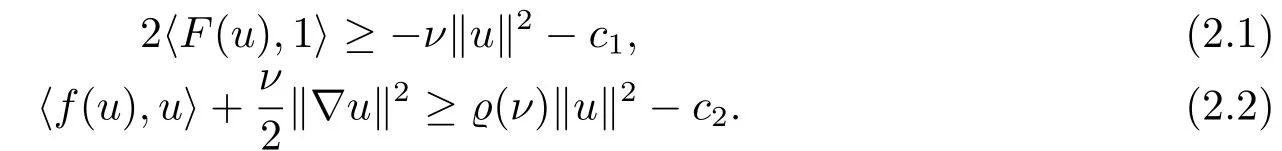
引理2.11[3]设ψ，r1，r2是非负局部可积函数，对δ ＞0，满足下面的微分不等式:

同时设定

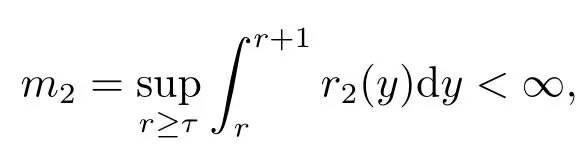
则

3.适定性和时间依赖吸收集

定理3.1[25-26]设(1.2)-(1.5)成立，则对任意初值zτ= (u0，u1，η0) ∈Hτ，在Ht中存在问题(1.1)的唯一解z(t)=(u(t)，ut(t)，ηt(s))，且对任意τ ∈R，t ≥τ，满足

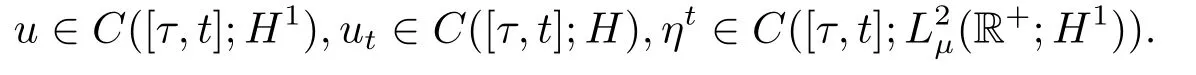
此外，设zi(τ) ∈Hτ是满足‖zi(τ)‖Hτ≤R(i = 1，2) 的两个初值，且zi(t)是(1.1)的解.则存在在C =C(R)＞0，使得

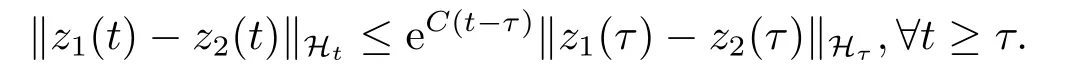
因此，系统(1.6)-(1.7)生成一个强连续过程U(t，τ)，其中U(t，τ) : Hτ→Ht，即U(t，τ)z(τ) ={u(t)，ut(t)，ηt(s)}.

引理3.2假设(1.2)-(1.5)成立，当初值z(τ)∈Hτ，存在C ＞0，使得

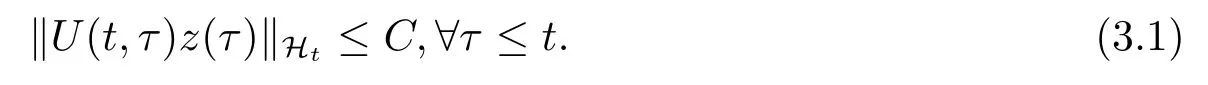
证设δ ＞0，取j =0，1定义

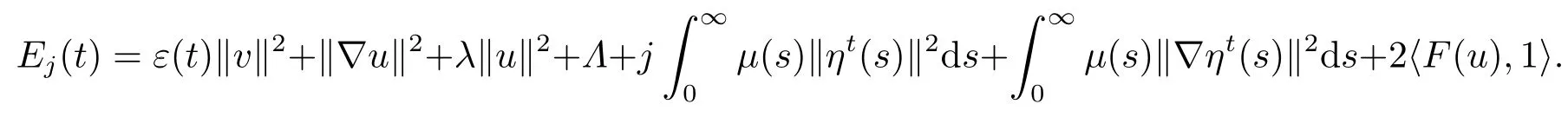
选取足够大的常数Λ ＞0，使得对任意t，Ej(t)≥0.此外，定义

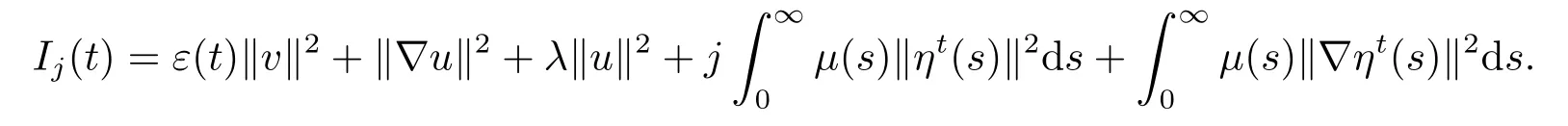
用v =ut+δu与(1.6)在L2(Rn)中做内积，得到

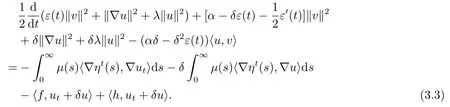
先用jηt与(1.6)2在(R+，H)上做内积，再用ηt与(1.6)2在R+，H1)上做内积后相加得到

根据(1.10)有

由(1.2)且将(3.3)和(3.4)加起来，并利用(3.5)有

根据Young不等式，(1.9)和(3.2)则有

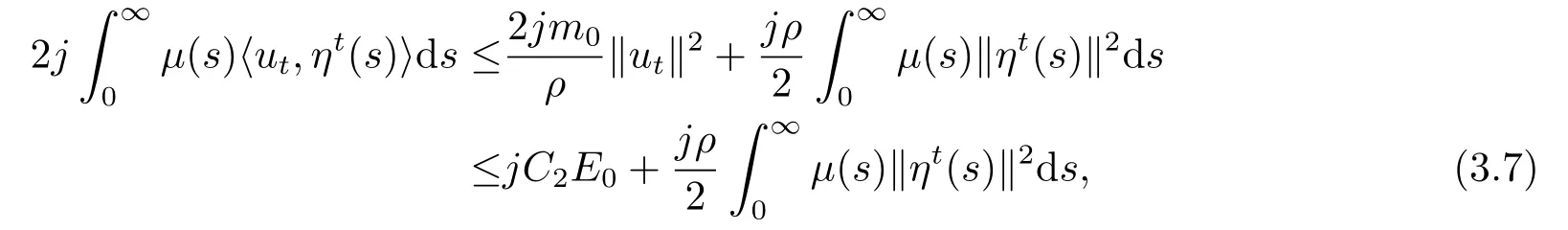
其中C2=2m0/ρC1且

利用(2.2)，有

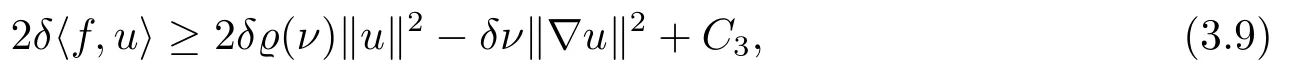
其中C3=2δc1.

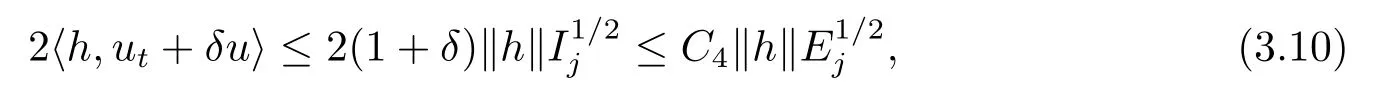
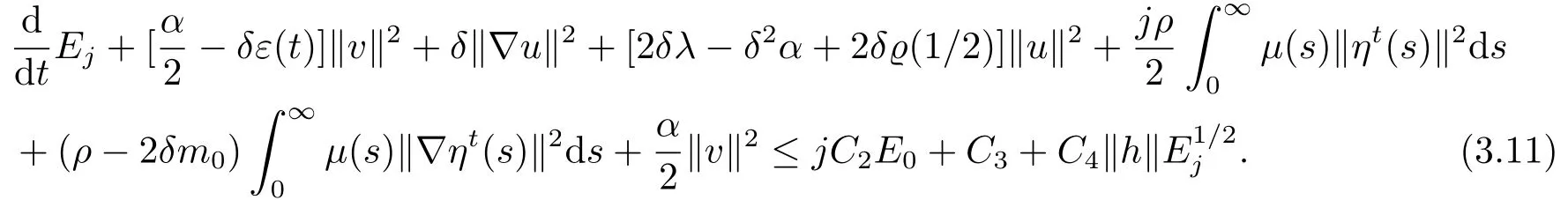
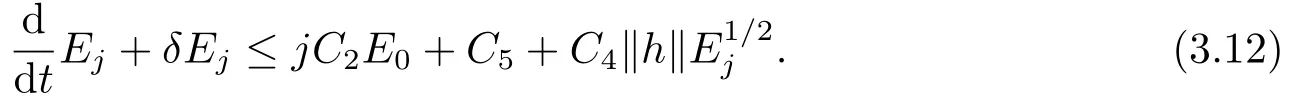
现在设j =0，1，利用引理2.11，得

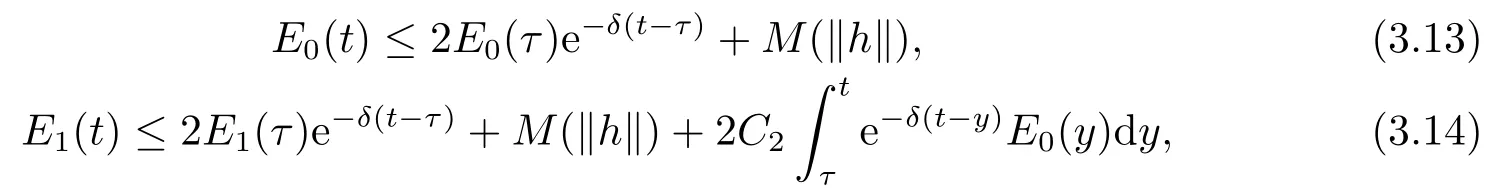
其中M :R+→R+是依赖于C4，C5，δ的递增函数.结合(3.12)有

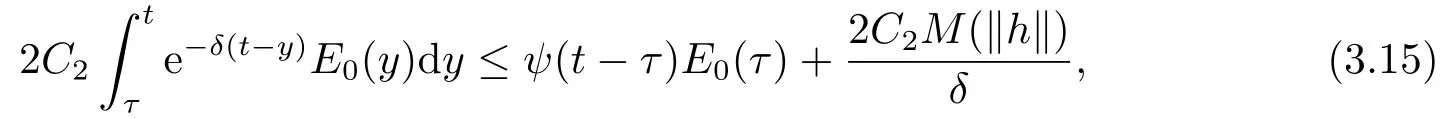
其中ψ(y)=4C2ye-δy(当y →∞，ψ(y)→0).由于E0(τ)≤E1(τ)，从(3.14)-(3.15)得到

因此，根据Young不等式及嵌入H1L4(Rn)，存在正常数C6，使得

从而，对z(τ)∈Hτ，存在C ＞0以及两个有界递增函数C1i: R+→R+，i =1，2，以及(3.16)中的函数ψ，根据(3.16)和(3.17)可得

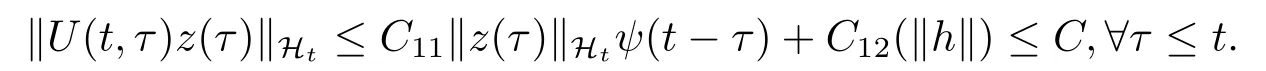
从引理3.2，我们可以得下面的结果:

引理3.3设条件(1.2)-(1.5)成立，对于引理3.2中的C ＞0，B = {Bt(C)} 为问题(1.1)生成过程{U(t，τ)}的时间依赖吸收集，且对R ≥C，有

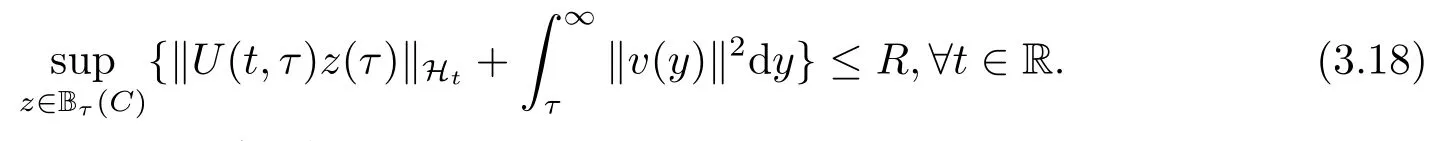
证结合(3.11)，且δ =0，得到

在[τ，t]上积分，当t →∞时，(3.18)就得到了证明.

对于非线性项f，为了得到无界域上过程的渐近紧性，我们还需要下面的条件:

其中l ＞0.

4.尾部估计

引理4.1设条件(1.2)-(1.5)成立，则对任意的ϵ＞0，存在T1= T1(ϵ)，使得当t ≥T1且k =k(ϵ)＞0，成立

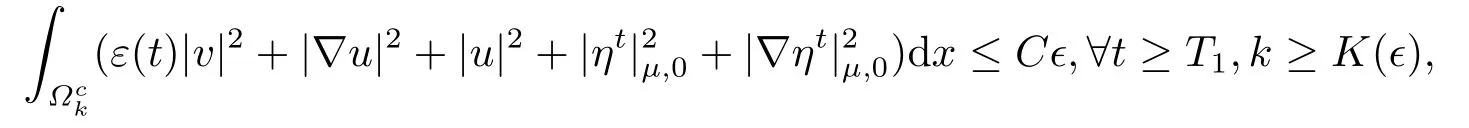
证选择合适的光滑函数θ，使得对任意的s ∈R+，有0 ≤θ(s) ≤1.具体地，当0 ≤s ≤1时，有θ(s)=0; 当s ≥2 时，有θ(s)=1，且存在一正常数使得max{|θ′(s)|，θ′′(s)|}≤

先给(1.6)2乘以并在Rn上做积分，然后用ηt与(1.6)2在(R+，H) 上做内积，最后用ηt与(1.6)2在(R+，H1)上做内积，记算后相加得

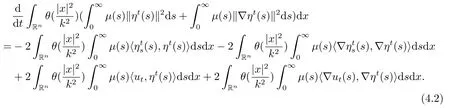
根据(1.10)有

将(4.1)和(4.2)加起来，并利用(4.3)有

根据Young不等式，(1.9)和(3.2)则有

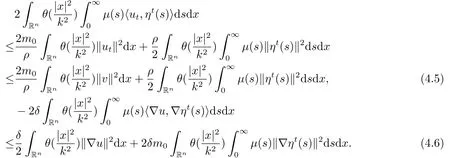
接下来，我们处理上述方程中的每一项，首先我们有

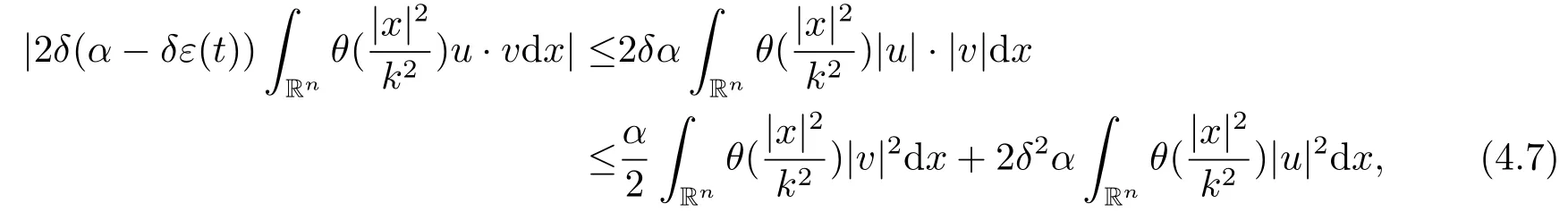
此外有

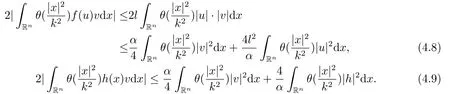
结合上面的估计得到

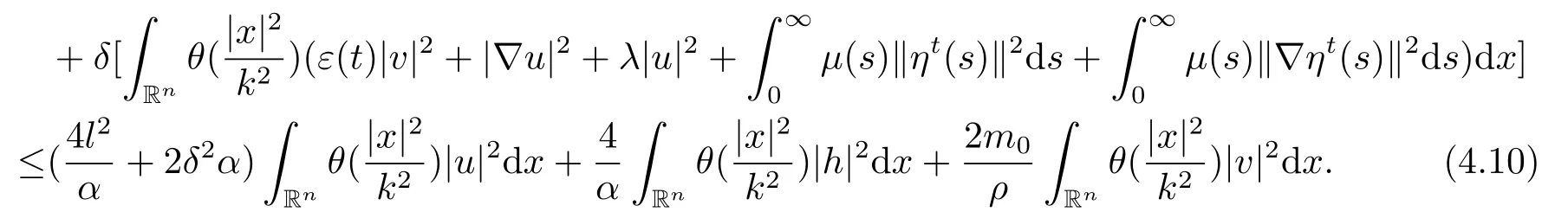
设k1(ϵ)＞0，且∀0 ＜ϵ＜1，使得k ≥k1(ϵ)，则

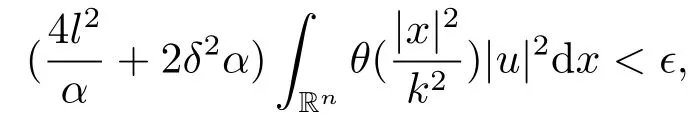
同理，设k2(ϵ)＞0，且∀0 ＜ϵ＜1，使得k ≥k2(ϵ)，则

此外，存在k3(ϵ)＞0，当k ≥k3(ϵ)，使得

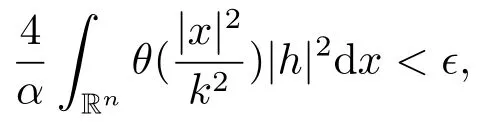
选取k0=max{k1(ϵ)，k2(ϵ)，k3(ϵ)}，当k ≥k0时，有

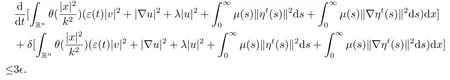
在[τ，t]上应用Growall引理，并结合引理3.3，得到

对给定ϵ＞0，设K =K(ϵ)，存在T1=T1(ϵ)，当t ≥T，且k ≥K(ϵ)，有

则得到

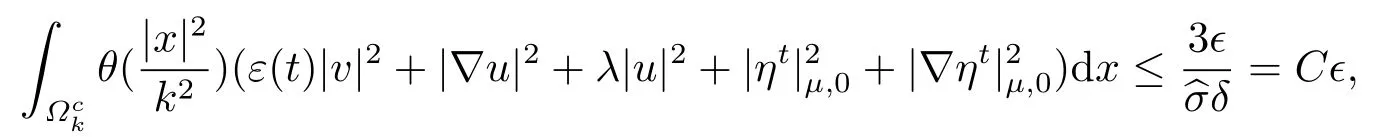
5.时间依赖全局吸引子的存在性

定理5.1设条件(1.2)-(1.5)成立，问题(1.6)生成的过程U(t，τ) : Hτ→Ht在H1(Rn)×L2(Rn)×(R+;H1(Rn))中存在一个不变的时间依赖全局吸引子U={At}t∈R.

接下来，我们利用渐近压缩函数方法得到系统(1.6)时间依赖吸引子的存在性.

引理5.2设条件(1.2)-(1.5)成立，h ∈L2(Rn)，问题(1.6)的解(un，unt，(s))对应的初值∈BT.则对任意k ＞0 及T(ϵ)＞0，令Ωk={x ∈Rn:|x|＜k}，成立:

在L∞(T，t;L2(Ωk))中，unt→ut弱*收敛.

在L∞(T，t;(Ωk))中，un→u弱*收敛.

在L2(T，t;(Ωk))中，un(t)→u(t)强收敛.

在L2中，un(T)→u(T)和un(t)→u(t)强收敛.

先验估计设(ui(t)，uit(t)，(s))为(1.6)的解，对应的初值为(∈{Bτ}τ∈R，且

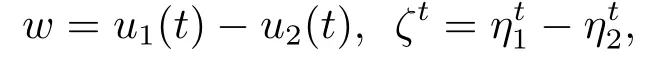
则ω(t)满足

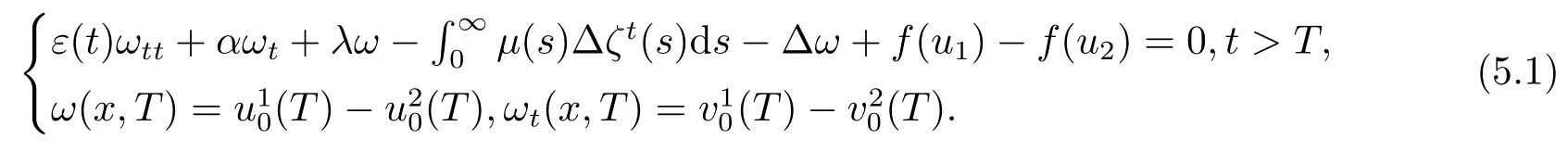
定义

用ωt与(5.1)在L2(Rn)上作内积，有

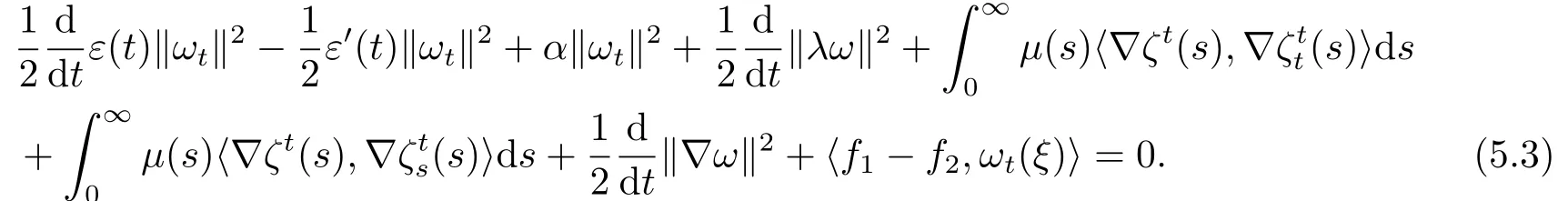
用ζt与在(R+，H)上做内积得到

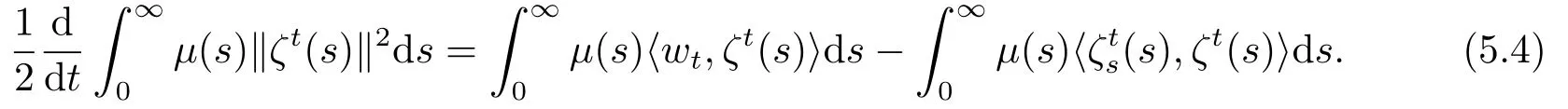
将(5.3)与(5.4)相加得

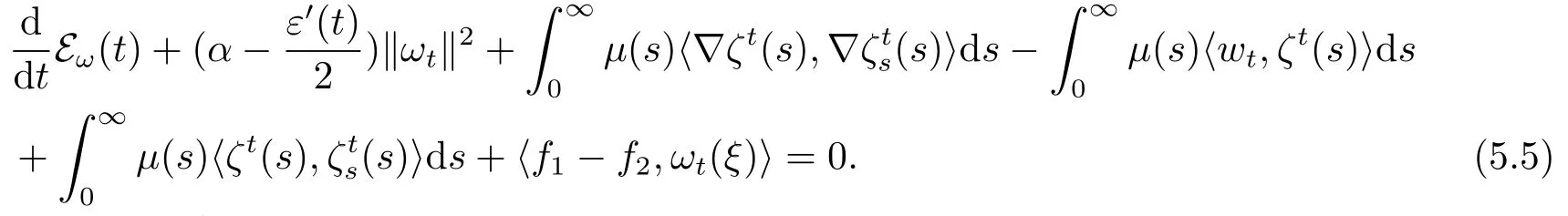
根据(1.10)，则有

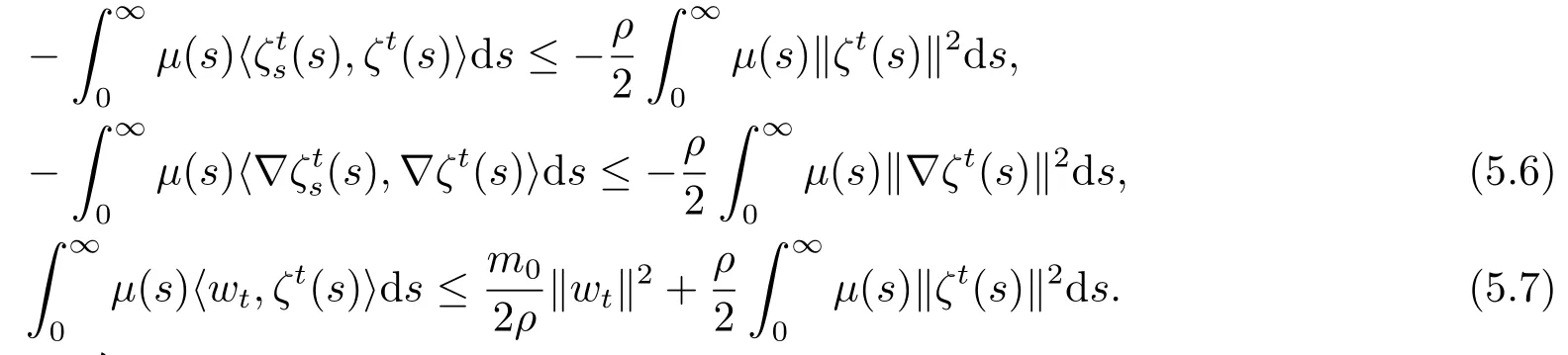
结合(5，5)-(5.7)有

对(5.8)在[s，t]上作内积，有

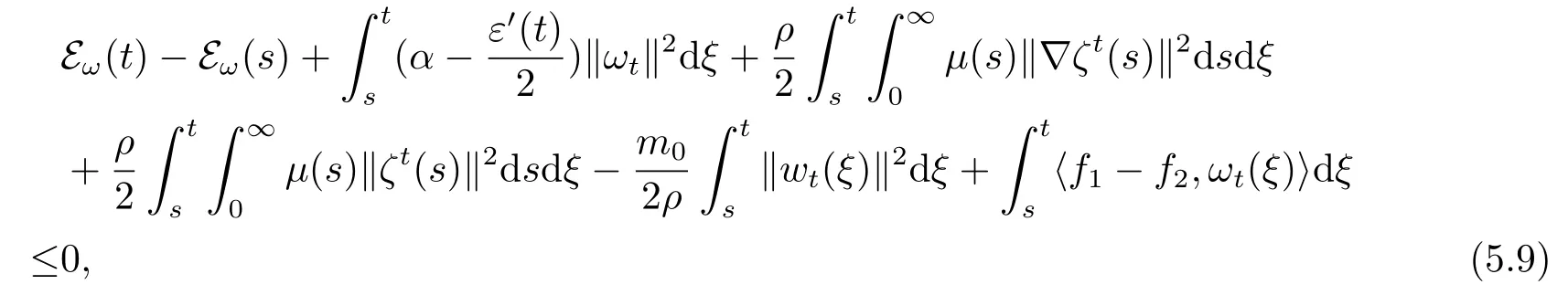
其中T ≤s ≤t，L ＜α，根据(1.3)式，得到

用ω与(5.1)式在Rn×[T，t]上作积分，得到

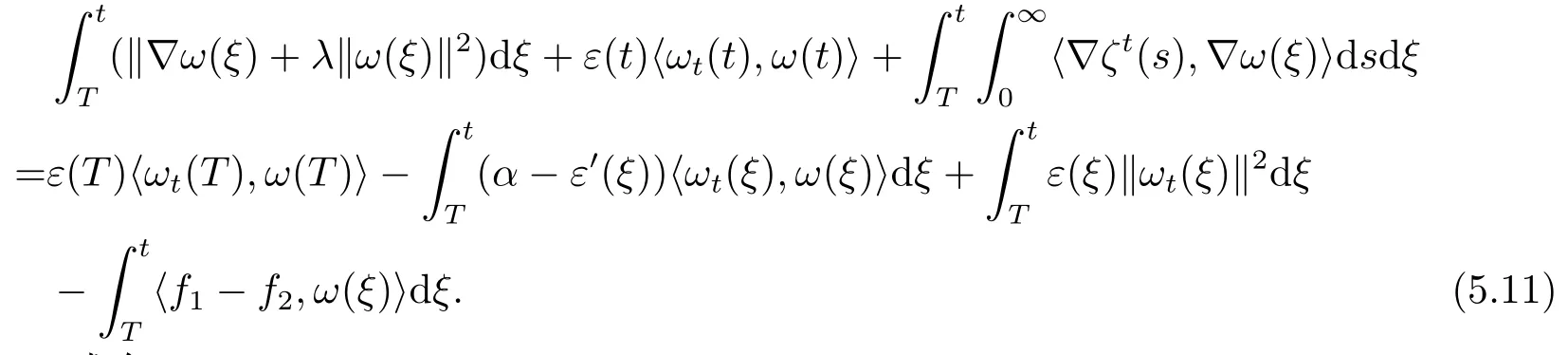
根据(1.10)式有

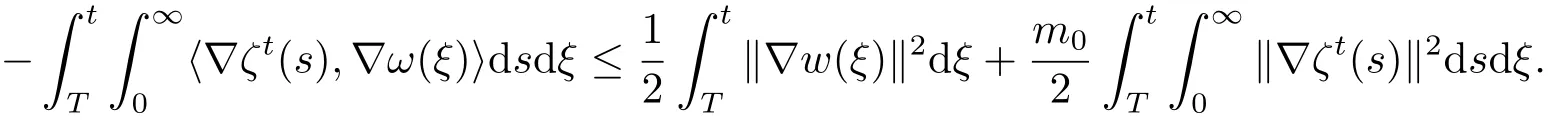
结合上式得

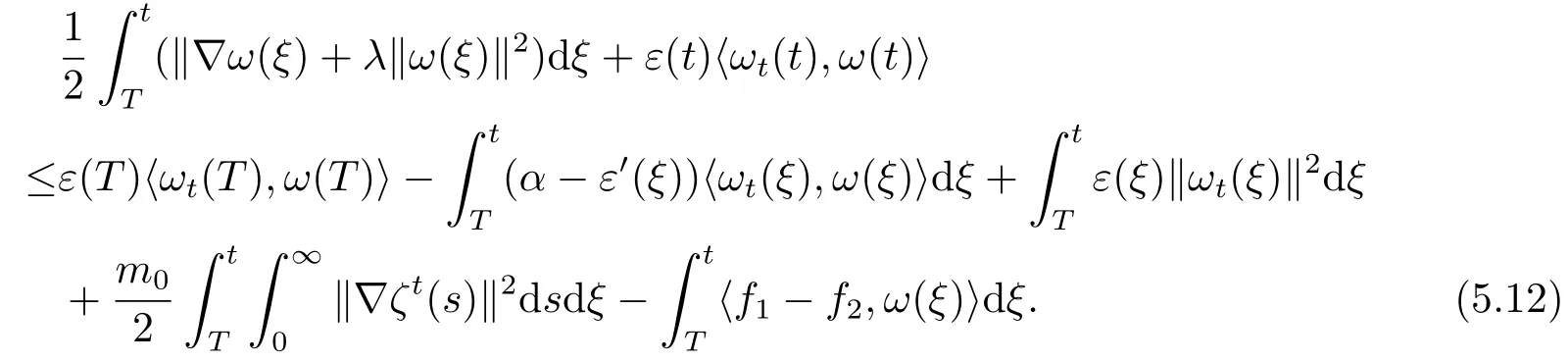
结合(5.11)(5.12)式，可得

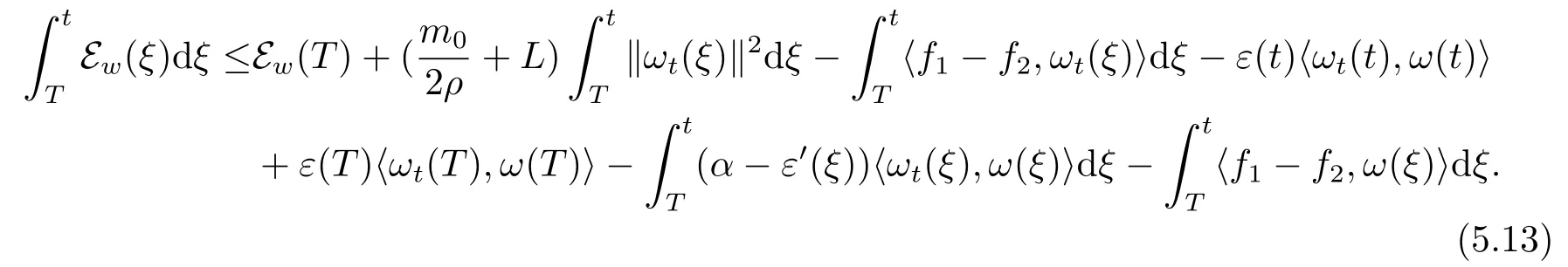
给(5.9)式在[T，t]上作积分，有

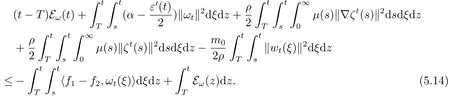
根据(5.13)和(5.14)有

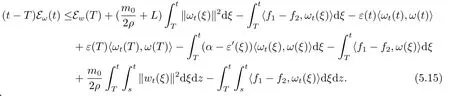
设

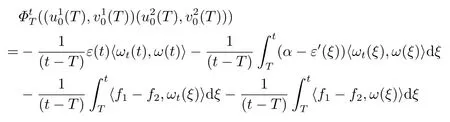
且

则有

定理5.3设条件(1.2)-(1.5)成立，则过程{U(t，τ)}是渐近压缩的，即，对任意固定t ∈R，有界序列且任意当n →∞时，τn→-∞，序列在H1(Rn)×L2(Rn)×(R+;H1(Rn))中是准紧的.

证设

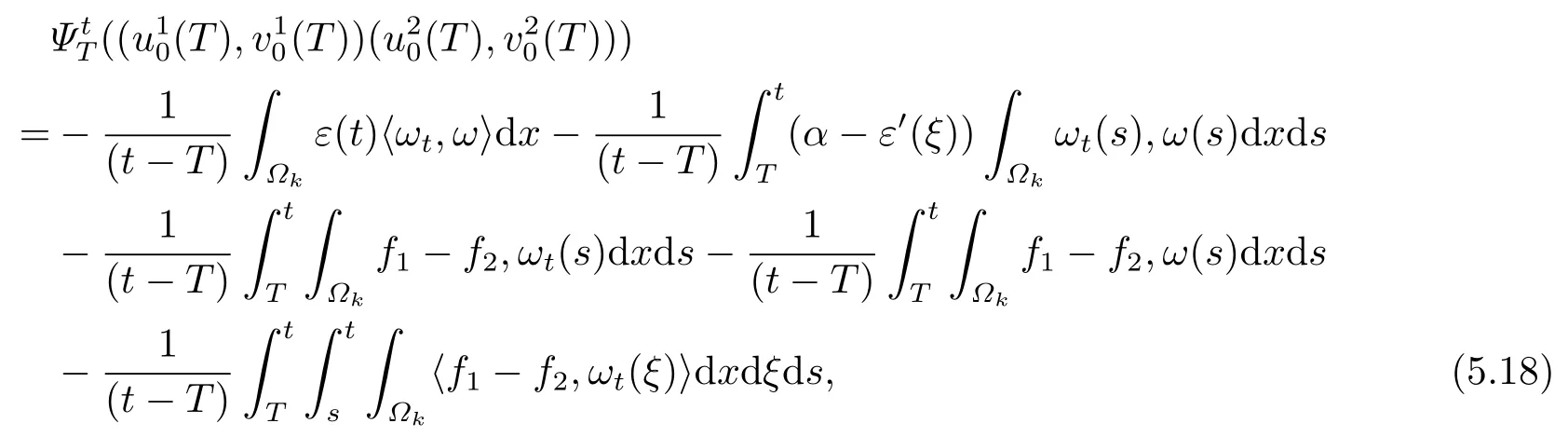
且

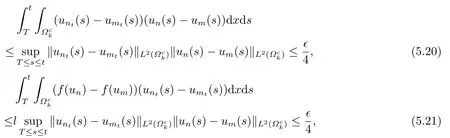
同样地当m，n足够大，我们可以得到

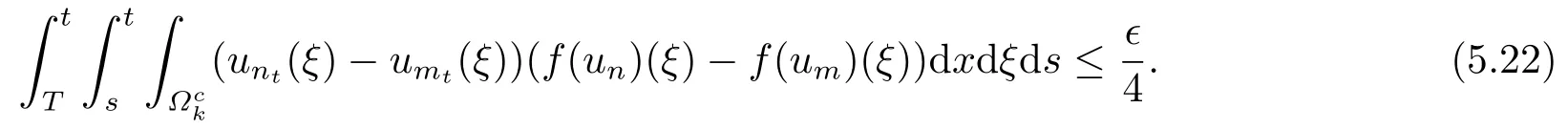
因此我们可以得到

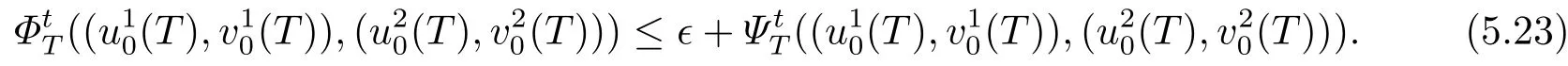
接下来，对任意固定ϵ＞0，令T ＜t使得t-T足够大，则

因此，根据定义2.6，2.7，对任意固定T，我们只需要证明(5.23)中是压缩函数.

现在，我们将处理(5.18)中的每一项.

首先，从引理3.2和引理5.2中，得到

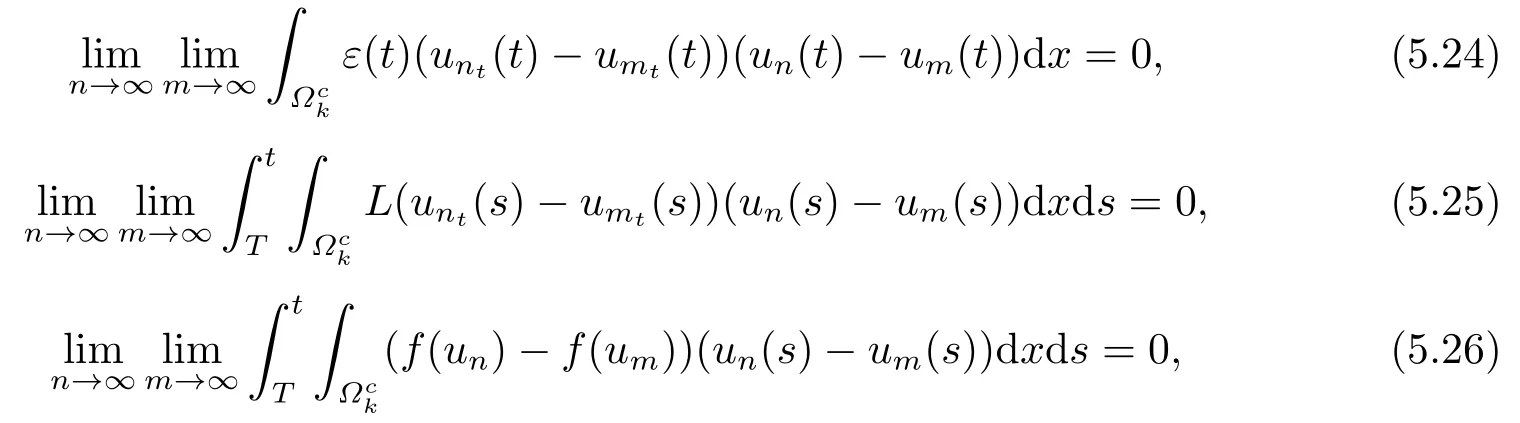
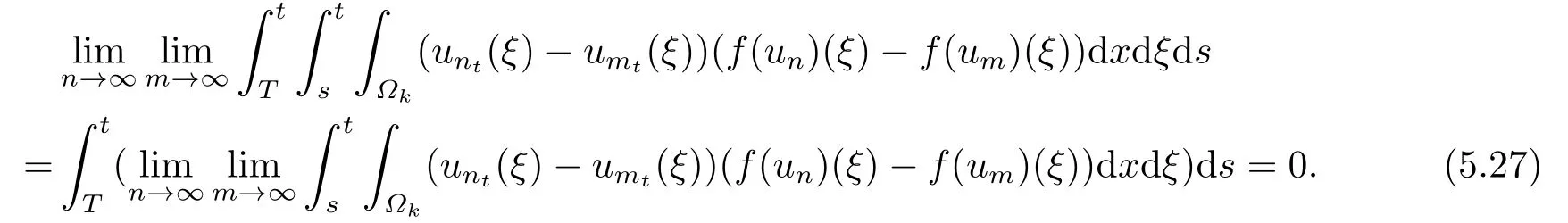
定理5.1的证明由引理3.2可知，U(t，τ)存在一致有界的时间依赖吸收集{Bt}t∈R.由引理4.1和引理5.3，可知U(t，τ)是渐近紧的，从而得到了H1(Rn)×L2(Rn)×(R+;H1(Rn))中时间依赖吸引子U={At}t∈R的存在性.