一种处理群体决策中个体偏好信息的新方法——部分共识模型

张曙阳，李 磊

（江南大学 商学院，江苏 无锡 214122）

0 引言

群决策（Group Decision Making，GDM）是一项普遍存在于各类组织的关键性活动，组织中人事、预算等业务的制定，通常需要群体讨论或会议完成。

在群决策中，多名决策者在沟通协商后表述自己的意见，并通过一定方法将个体观点整合为群体观点。决策者对群体观点的认可度越高，决策结果就更为合理，决策执行就更为顺利。因此在群决策中，促使决策者交流沟通，逐渐形成共识水平更高的群体观点，是非常有必要的。

共识是一个相对模糊的概念，在理想情况下，共识应是所有决策者的对某方案一致性观点，此一致性观点能完全代表群体意见。而实际上，完全共识是极难形成的。因此，更为温和、折衷的共识标准，如除去一人的一致共识、除去两人的一致共识，或是人的一致共识，在现实群体决策中是更为适用的。除去这些基于实数的共识测度，Kacprzyk引入了模糊多数的概念，利用模糊语言量词定义了“软共识（Soft Consensus）”测度［1，2］。

以数学方法达成共识的决策模型始于Coch及French的开创性研究，该研究表明，在制造业组织生产程序改变的决策中，如果受决策结果影响的个体能够参与到决策过程，组织的生产率将更高、离职率将更低［3］。自此，共识决策理论不断发展，其主要研究方向可以划分为三类：

第一，最大共识水平决策模型。在此类模型中，共识水平通过个体观点与群体观点的相似度、距离测度等指标计算得出，学者们求解最能被个体所接受、共识水平最高的群体观点。近年来此类模型发展的趋势，是将决策共识水平与个体偏好矩阵（模糊偏好关系、乘法偏好关系）的一致性水平共同优化。

Jacinto基于目标规划理论，来最小化个体观点与群体观点的不相似度，并提出在“多数人原则”及“少数人原则”之间平衡的共识框架［4～6］。Fedrizzi最小化“个体至群体观点的偏差”及“个体观点变动值”的加权之和［7］。Lee在基于梯形模糊数的群体性决策中，定义了梯形模糊数的相似度系数，通过优化专家权重，最小化个体评价矩阵与群体评价矩阵的加权不相似度［8］。Liu改进了Lee的模型，为各个专家可承受的不相似度（妥协度）设定不同的上限［9］。Pegrycz提出“信息粒度（information granularity）”概念，利用信息粒度，将AHP法中个体偏好关系由单值拓展至区间，在该区间内最大化共识水平及偏好矩阵一致性［10］，Cabrerizo将此法拓展至模糊综合评价［11］。Dong提出了犹豫语言群决策环境下的共识决策模型，以共识水平超出设定阈值为约束条件，利用混合0-1规划来最小化被调整观点的数量［12］。

第二，基于“moderator”的共识决策模型。此类模型将共识水平视为决策质量的指标，当群体观点的共识水平小于设定阈值时，“moderator”将会向共识水平较低的个体提供观点修改意见，并重新计算共识水平，当共识水平超出阈值则停止迭代。

Herrera基于软共识（Soft Consensus）理论，提出了面向语言及多粒度语言信息的共识支持系统（Consensus Support System，CSS），最早构建了基于“moderator”的共识决策的基本框架［13～15］。Xu设计了达成共识的自动算法，当相似度小于设定阈值时，程序将自动调整个体及群体偏好值，使共识水平超出设定阈值［16］。Alonso设计了一套基于“moderator”的共识决策支持系统，可以处理模糊、语言、多粒度语言偏好信息［17］。Chu定义了直觉模糊偏好关系的加性一致性，设计了自动迭代程序，使个体观点逐渐向群体观点靠拢，不断提升评价矩阵的共识水平及一致性水平［18］。Wu基于社会信任网络来计算个体权重，通过OWA算子集结得到群体观点，并找出共识水平较低的个体建议其修改评价意见［19］。Zhang提出个体观点的变动成本，应与专家观点质量相关，并提出了不完全语言分布评估（Incomplete Linguistic Distribution Assessments，ILDA）的概念，当个体观点与群体观点的共识水平不满足标准时，moderator会给个体反馈修改的意见［20］。

第三，最小共识成本决策模型。此类模型与最大共识水平模型较为相似，但优化目标并非共识水平最高，而是共识成本最低。共识成本是指改变个体观点至群体观点的所耗费的调解成本，其取值通常为个体观点与群体观点偏差的线性或二次函数。

Ben-Arieh最早提出最小共识成本模型（Weighted Consensus at Minimum Cost Problem，WCMC），该模型需要找出最优的群体观点，以最小化个体观点转移至群体观点的协调成本［21，22］。Ben-Arieh在WCMC基础上，提出新的约束条件：（1）最小共识成本，并限定个体观点与群体观点的偏差在设定范围内；（2）在成本限制下最大化形成共识的专家人数。Zhang将集结算子与WCMC相结合，使用集结算子将个体观点转为群体观点，Zhang主要研究了OWA 算子及其权重为的特例［23］。Zhang将结合OWA算子的WCMC模型转为0-1整数规划问题，并提供模型中OWA算子任意权重的解法［24］。Gong将区间数形式的个体观点与WCMC相结合，并以线性规划求解［25］。

本文研究对象为最小共识成本决策模型。本质上，在以Ben-Arieh为代表的最小共识成本决策模型中，共识更类似于追求“一致同意”的完全共识［21，22］，共识成本的计算、群体观点的形成，需要考虑所有个体观点，而这存在两个问题：

其一，部分因利益相关而拥有明显偏好的个体，可能恶意操控自己的观点，使得最终得出的群体观点对己方有益，使群体观点存在一定偏差。Zhang通过引入OWA算子，去除个体决策信息的极大与极小值，在一定程度上解决了此问题［23］。但OWA算子难以实现更为复杂的共识条件，更无法适用于难以排序的多维评价信息（区间数、直觉模糊数）。

其二，当群体中大部分个体向小部分个体观点妥协带来的共识调解成本，大于该小部分个体可为群体带来的收益时，考虑所有的个体观点反而会降低群体的总效益。

因此，本文承接 Ben-Arieh及Zhang的研究［21～23］，基于最小共识成本决策模型，提出部分共识模型，即：共识调解成本的计算，应只考虑满足一定数量关系的个体，群体观点的形成也应只与这些个体相关。本文将“一定数量关系的个体达成共识”定义为“共识条件（Consensus Condition）”。如在“80%的个体形成共识”的共识条件下，部分共识模型求得的群体观点，不仅共识调解成本最小，形成共识的个体数量，也会超出个体总数量的80%。

1 理论框架

1.1 最小成本的共识决策模型

假定群决策的决策者集为E＝｛e1，…，en｝，权重集为W＝｛w1，…，wn｝，oi表示第i名决策者的初始观点表示其改变后的观点，o表示基于n名决策者观点而得到的群体观点，ci为改变决策者i观点付出的单位成本。现有的几种衡量个体观点与群体观点偏差的方法中，距离测度是最常用的方法之一。在最小共识成本的决策模型中，决策者i的观点oi与群体观点o的差值，以p-范数计算：

p可取1或2，分别代表Manhattan距离和Euclidean距离，p＝∞时，公式取值等于oi与o在单维度上的最大差值。Ben-Arieh最小成本下的加权共识 （Weighted Consensus at Minimum Cost，WCMC）问题，可表示为求解最优观点［21，22］：

Ben-Arieh给出p＝1时，该模型的求解算法。考虑到决策者i在不同维度上的妥协成本不具备线性可加性，Ben-Arieh还给出观点偏差等于（‖oi-o‖2）2时，模型的求解算法［21］。

Ben-Arieh提出，决策者观点oi足够接近群体观点o时即可认为形成共识，并无需额外调解成本，将其定义为共识下的最小成本（εConsensus at Minimum Cost，εWCMC）问题［21］。此时，εWCMC可表述为：

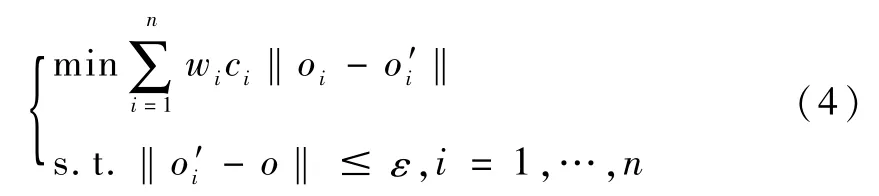
Zhang在εWCMC中引入OWA算子，新增约束条件，o＝Zhang利用权重为｛0，1／（n-2），…，1／（n-2），0｝的OWA算子，去除个体决策中的极大值及极小值，保障群体观点的科学合理。

在群决策中，决策参与者都有自己的个体目标，并且经常战略性地操纵偏好信息来实现自己的目标。如为避免此问题，在奥运体操项目中，在来自各国评委对运动员表现打分之后，最大及最小评分将被舍去，运动员的评分由剩余评委的评分算术平均得出［23］。

在WCMC中，衡量群体观点质量的标准，是调解所有个体观点所需耗费的成本。成本是相对于收益的概念，组织支付调解个体观点的成本，是因参与群决策的个体都会为组织带来显性或隐性的资源。基于WCMC决策过程中，部分个体将使群体观点产生的偏移，以及带来的调解成本，可能超出该部分个体为组织带来的资源收益。换言之，将这部分个体排除在决策之外，组织虽减少一些可调动资源，但是会减少更多的调解成本，总效益反而更高。

此两例表明，群决策中有意识的考虑在部分决策者内形成共识，是非常有必要的。

决策者权重，是个体调动资源能力的重要体现，也可视为个体带来收益的重要指标。若形成共识决策者的权重和超出设定值，即可认为组织可调动的资源满足决策实施的要求。因此，在决策者权重超出设定值的情况下，本文将最小化个体的共识调解成本，设为优化目标。

1.2 最小成本的部分共识决策模型

定义1部分共识

决策者集为E＝｛e1，…，en｝，权重集为W ＝｛w1，…，wn｝，若基于满足一定数量关系的、群体中的部分个体Q，得出群体观点o，则称o为部分共识：

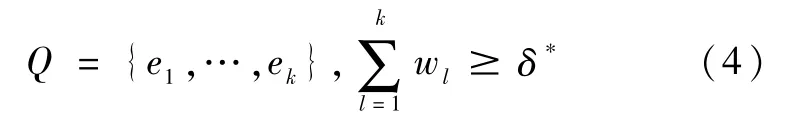
部分共识的核心思想，是基于部分个体的观点，得出综合效益最高的群体观点。

定义2共识条件

部分共识模型中，对部分决策者G1的数量关系要求，称共识条件δ*。

决策者幂集为P（E），对任意决策者幂集的元素P1，P1∈P（E），若：

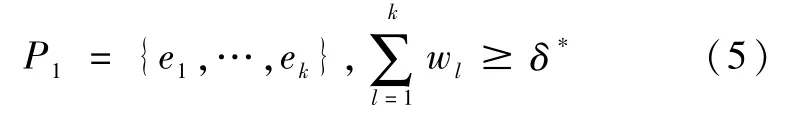
则称，P1满足共识条件，反之，则称P1不满足共识条件。共识条件δ*可视为决策实施所需要的、最低限度的可调度资源。若某一决策者组合P1满足共识条件，则认为其可调动足够的资源支持决策，反之，则认为P1并不拥有足够的资源。

定义3共识空间

所有满足共识条件δ*的、决策者幂集的元素为G（δ*），称G（δ*）为当前共识条件下的共识空间：

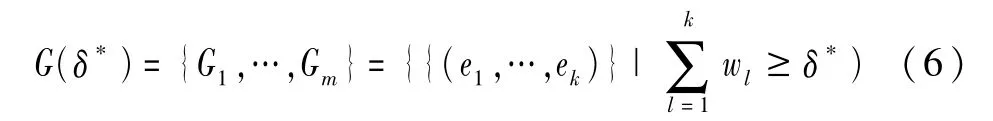
共识空间是所有满足共识条件的、决策者的组合，是部分共识模型的优化空间。共识空间内的任一决策者组合，都可调动足够的资源支持决策。

定义4部分共识模型

决策者观点为oi，单位观点偏差的调解成本为ci，共识条件为δ*，群体观点o在共识空间的调解成本为C（o）：

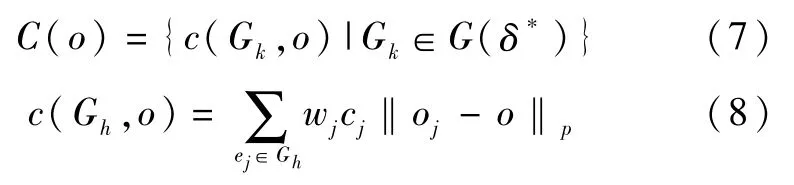
c（GK，o）为促使部分决策者Gh达成群体观点o需付出的调解成本。

部分共识模型下的最优群体观点为o*：

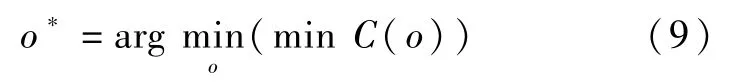
在形成共识的决策者中，达成群体观点o*将付出最少的调解成本，此部分决策者满足共识条件，其可调动的资源，也满足决策实施需求。

2 部分共识模型的求解

部分共识模型的求解可划分为三步：第一，生成满足共识条件δ*的共识空间；第二，确定部分决策者中的最优群体观点；第三，确定所有决策者组合中的最优群体观点。

2.1 生成共识空间

共识条件为δ*，决策者集为E＝｛e1，…，en｝，决策者权重集为W ＝｛w1，…，wn｝，生成共识空间，可以视为找出所有权重和超过δ*的决策者集的子集。

此问题类似于子集和问题（Subset Sum problem）：给定集合S，找出元素和为t的所有子集。子集和问题是背包问题（Knapsack problem）的特例，也是NP-hard问题。

本文问题为找出所有元素和超出t的子集，难度更高，同样为NP-hard问题，遍历集合元素的所有组合是目前唯一可行的解法。当t＝0时，算法需生成子集，算法时间复杂度为O（2n）。

在部分共识模型中，共识条件δ*代表决策可调用资源的水平，δ*一定大于0。因此针对δ*＞0时，本文对穷举算法进行优化，跳过生成一定不满足共识条件的子集，以提升算法的运行效率。

算法1初始化：

（1）将权重W＝｛w1，…，wn｝集内元素，按递增规则进行排序，得集合W′；

（2）设k＝0，B＝Ø，G＝Ø。

运行步骤：

计算集合W′中第0个至第k个元素的和，记为sum（1：k），当sum（1：k）≤1-δ*时：

结束：

将集合B内满足共识条件δ*的元素，添加至集合G：G←｛（e1，…，ek）｜Bi∈B，Bi＝｛w1，…，wk｝，

输出G。

证明sum（1：k）＞1-δ*时，集合内元素不满足共识条件δ*。

将权重W＝｛w1，…，wn｝集按递增进行排序，得集合W′＝｛wσ（1），…，wσ（n）｝，wσ（1）≤wσ（2）≤…≤wσ（n）。

将sum（A）定义为对集合A内元素求和，如sum（｛1，2，3｝）＝6。

因为sum（1：k）＞1-δ*，所以sum（｛wσ（1），…，wσ（k）｝）＞1-δ*，所以sum（｛wσ（n+1-k），…，wσ（n）｝）＜1-δ*。

因为集合 W ′中前 k个最大的元素为｛wσ（n+1-k），…，wσ（n）｝，所以对所有，所以中元素均不满足共识条件。

证毕

2.2 确定最优部分群体观点

群决策的评价方式包括排序、效用值、偏好关系等，评价载体可划分为单维度评价值（实数、模糊数等）及多维度评价值（区间数、直觉模糊数、梯形模糊数等）。

在Ben-Arieh与Zhang的共识决策模型中，决策者给出的均为单维度评价值［21～24］。但多维度评价值在共识决策的相关研究中常有出现，如Lee的梯形模糊数、Liu的区间模糊偏好关系、Chu的直觉模糊偏好关系等研究［8，9，18］。

因此，基于Ben-Arieh的研究，本文给出部分共识模型在单维度及多维度评价值下的求解算法。

决策者集为E＝｛e1，…，en｝，决策者权重集为W＝｛w1，…，wn｝，评价方案集为F＝｛f1，…，fm｝，评价属性集为A＝｛a1，…，ap｝，ci为改变决策者观点付出的单位成本。

2.2.1 单维度评价值

Chiclana的研究表明，在基于Moderator的共识决策模型中，相较于其它距离函数，Manhattan及Euclidean距离函数可加速群体共识的形成［26］。因此，本文与Ben-Arieh一致，以Manhattan距离计算决策者的观点与群体观点的差值：

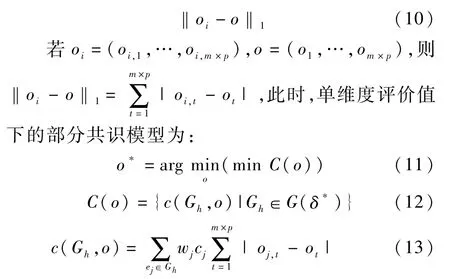
共识空间G（δ*）可由算法1求得，对共识空间G（δ*）内决策者组合Gh，该决策者组合的最优群体观点记为向量，向量的第t行值记为

算法2：

初始化：

将名决策者观点按递增规则进行排序，oσ（1），t≤oσ（2），t≤…≤oσ（u），t，设L＝｛1｝，R＝｛u｝，l＝1，r＝n。

运行步骤：

当L≠r时：

结束：

输出oσ（r），t，oσ（r），t为最佳群体观点。

算法的有效性证明见Ben-Arieh［21］。

2.2.2 多维度评价值

当决策者给出多维度评价值时，其评价向量记为oi＝（oi，1，…oi，m×p），第t行评价信息记为oi，t。若评价信息维度为d，则当d≥2时，无法直接用p范数计算向量oi与o的差值。因此，首先以p范数计算向量t行评价信息oi，t与ot的偏差：

p＝1时，评价信息各个维度上的偏差存在可加性。举例而言，若ot＝［0，1］，此时ot与［3，4］和［0，7］的偏差相同，均为6。但从概率角度，［0，7］的偏差显然要更高，取p＝1并不适当。p＝2时，oi，t与ot差值等同于其Euclidean距离，最优群体观点与所有个体观点的Euclidean距离之和最小。此问题等同与物流选址领域经典的Fermat点问题，虽已有成熟的方法予以解决（重心法、梯度下降法、牛顿法、模拟植物生长算法等），但计算消耗稍高，且会增大模型的复杂程度。

Ben-Arieh提出以2范数的平方，衡量个体观点与群体观点的偏差［21］，在此距离函数下，多维度评价值的偏差等于：

对共识空间G（δ*）内决策者组合Gh，该决策者组合的最优群体观点记为向量，向量t行值为等于：

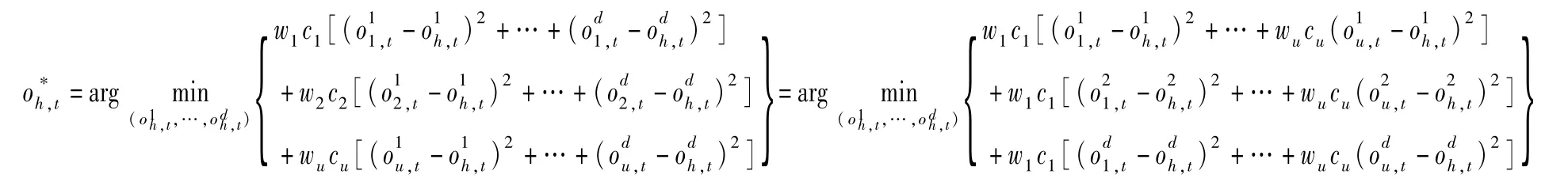
此时，该问题转为易于解决的最小二乘问题。设：

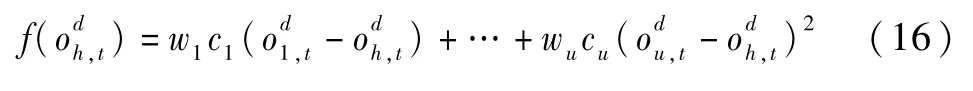
2.3 确定最优群体观点

部分共识模型下的最优群体观点，有着最小的共识调解成本。3.2节已完成在任意决策者组合Gh中，求解调解成本最小的、部分最优群体观点的共识调解成本为：

因此，确定最优的群体观点，仅需计算所有决策者组合、在其部分最优群体观点下的调解成本，并从中选出最小值即可：

3 基于部分共识模型的群决策方法

本文构建的部分共识模型框架适用于群决策中的单维度及多维度评价值，现分别给出实数及直觉模糊数的群决策方法。

决策者集为E＝｛e1，…，en｝，决策者权重集为W＝｛w1，…，wn｝，评价方案集为F＝｛f1，…，fm｝，评价属性集为A＝｛a1，…，ap｝，ci为改变决策者i观点付出的单位调解成本，δ*为群决策的共识条件。

3.1 基于实数的群决策方法

使用部分共识模型，处理基于实数的群决策问题，具体步骤如下：

Step 1使用算法1，得到共识条件δ*下的共识空间G（δ*）。

Step 2对共识空间内的任意决策者组合Gh，使用算法2，确定最优部分群体观点。

Step 3使用公式（19），计算所有决策者组合G（δ*）中的最小共识调解成本C。取C中最小值，并将最小值对应的评价向量确定为最优群体观点o*，从而得到最优决策方案。

3.2 基于直觉模糊数的群决策方法

首先给出直觉模糊数的基本定义。

定义5［27］设X是一个非空集合，则称

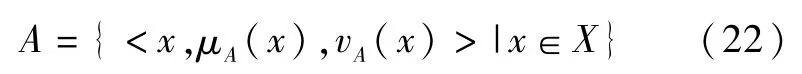
为直觉模糊集，其中μA（x），vA（x）分别是X中元素x属于A的隶属度和非隶属度：

为X中元素x属于A的犹豫度，称α＝（μα，vα）为一个直觉模糊数（IFN）。

定义6［28］对直觉模糊数α＝（μα，vα），其得分函数S为

s（α）∈［-1，1］，s（α）为α的得分值。

使用部分共识模型，处理基于直觉模糊数的群决策问题，具体步骤如下：

Step 1使用算法1，得到共识条件δ*下的共识空间G（δ*）。

Step 2对共识空间内的任意决策者组合Gh，使用公式（18），确定最优部分群体观点。

Step 3使用公式（19），计算所有决策者组合G（δ*）中的最小共识调解成本C，取C中最小值，将最小值对应的评价向量确定为最优群体观点o*。

Step 4使用公式，计算评价向量o*中各个选择项的得分，从而得到最优决策方案。

4 算例

算例1本算例改编自Zhang［23］，在准备购置一处公寓时，5名家庭成员对5个备选项进行评价，选择项记为fr，r＝1，…，5，5名家庭成员记为ei，i＝1，…，5权重向量为（0.2，0.3，0.1，0.2，0.2）T。家庭成员ei以区间［1，5］内实数评价备选项fr，记为，其取值越高，偏好程度越强。

共识调解成本为｛c1，c2，c3，c4｝＝｛1，1，1，2，2｝，共识条件为δ*＝0.8。以本文提出的部分共识模型处理决策信息，初始评价值为表1。

Step 1生成共识空间，使用算法1，求解权重和超过δ*＝0.7的所有决策者组合G（δ*），得表2。

表1 备选项评价值

表2 共识空间

表3 最优部分群体观点

表4 最小部分共识成本

Step 2使用Ben-Arieh提出的算法2，求解各决策者组合的最优部分群体观点，得表3。

Step 3使用公式，计算各决策者组合的最小部分共识成本，得表4。最小部分共识成本为3.5，因此为最优群体观点＝［3，4，2，2，4］，备选项2和4为最优选择。

值得注意的是，本算例中决策者组合G0包括全部决策者，其最优群体观点为，但共识调解成本却截然不同。这是因为部分共识模型以综合效益最大化为目标，仅对可调动资源满足决策需求的决策者群体进行调解。

算例2本算例改编自Ouyang［29］，一家制造公司需要选择某个关键零部件的供应商，假定存在5个选择项fr＝，r＝1，…，5，4名评审专家ei，i＝1，…，4，专家权重向量为（0.3，0.2，0.3，0.2）T。评审专家使用直觉模糊数（Intuitionistic Fuzzy Values，IFVs），从产品成本（a1）方面评估各个潜在供应商的表现，专家ei对供应商fr的评价记为

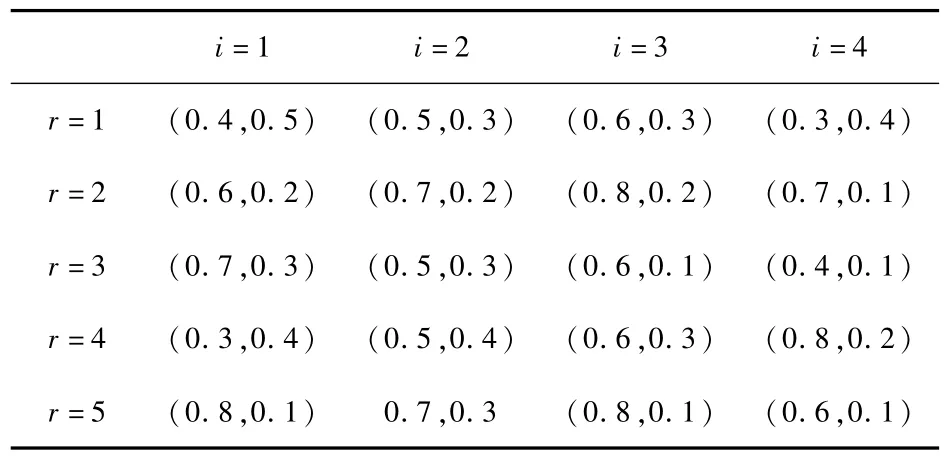
表5 备选项评价值

共识调解成本为｛c1，c2，c3，c4｝＝｛1，1，1，2｝，共识条件为δ*＝0.8。以本文提出的部分共识模型处理决策信息，初始评价值为表5。

Step 1生成共识空间，使用算法1，求解权重和超过δ*＝0.8的所有决策者组合G（δ*），得表6。

Step 2使用公式，求解各决策者组合的最优部分群体观点，得表7。

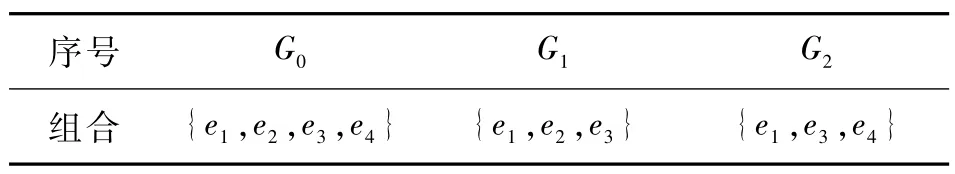
表6 共识空间

表7 最优部分群体观点

Step 3使用公式（19），计算各决策者组合的最小部分共识成本，得表8，最小部分共识成本为0.5，因此为最优群体观点。

表8 最小部分共识成本

Step4 使用公式（26）计算向量中模糊评价值的得分，得因此，供应商5是最优选择。

5 结论

本文改进了Ben-Arieh及Zhang的最小共识成本决策模型。在界定了部分共识、共识条件、共识空间的基础上，本文构建了部分共识模型，提出了一种处理群决策中单维度、多维度个体评价信息的新思路：群决策中群体观点的形成，应仅基于群体中、满足一定数量关系的部分个体。在保障形成共识的部分个体所调动资源满足决策实施的前提下，规避因利益相关而持有极端观点的个体，同时也避免绝大多数个体向少部分个体妥协造成的群体总效益下降。

本文给出了共识空间及最优群体观点的求解算法，证明了算法的有效性，同时还给出在部分共识模型框架下，基于实数及直觉模糊数两类评价值的群决策方法。实际案例的分析结果，表明了本文方法的实用性和可行性。