电流变方程解的稳定性
2021-01-07许文彬
许文彬
(集美大学理学院,福建 厦门 361021)
0 引言
文中将考虑进化方程

(1)

u|t=0=u0(x),x∈Ω,
(2)
总是需要的。若α=0,关于这个方程有一些研究结果:文献[3]研究了各向异性的变指数方程解的存在性;文献[4]假设在没有对数Hölder连续性的条件下,研究了方程变指数方程初边值问题解的存在唯一性;文献[5]研究了变指数含有时间变量的解的梯度估计;文献[6]研究了相关解的Hölder连续性。
如果p(x)=p,文献[7]研究了方程

(3)
发现,与通常的边界条件
u(x,t)=0,(x,t)∈∂Ω×(0,T)
(4)
相比,仅部分边界条件
u(x,t)=0,(x,t)∈∑p×(0,T)
(5)
与方程(3)相匹配。


1 定义

定义2 设u(x,t)为具有初值(2)的方程(1)的弱解。如果u在迹意义下满足部分边界条件(5),则称u(x,t)为具有初始边界条件(2)、(5)的方程(1)的弱解。

2 主要结果
首先,主要讨论基于部分边界值条件的弱解的稳定性。
定理1 设b(s)是Lipschitz函数,u和v分别是方程(1)具有相同的局部齐次边值条件
u|Σp×(0,T)=0=v|Σp×(0,T),
(6)
和不同的初值u0(x)、v0(x)的两个弱解。如果
(7)
α |g(x)|≤cρ(x), (8) 则 当然,定理1 的条件(7)只是证明了一类解的稳定性。其实从下面的证明可以看出,如果不是部分边界条件,而是整个边界条件(4),那么只要选取gn(u-v)作为检验函数,无需条件(7),可以得到下面的推论1。 如果α≥p+-1,方程(1)的弱解由于缺乏正则性而难以定义其在边界上的迹,必须研究不带边界值条件的弱解的稳定性。 定理2 设u和v分别是方程(1)具有不同初值u0(x)、v0(x)的两个弱解。如果α>p+-1,常数β≥max{α/p-,1},且 |g(x)|≤cρβ(x), (9) (10) 其中,Ωλ={x∈Ω:ρ(x)=dist(x,∂Ω)>λ}。 对于任意给定的正整数n,设gn(s)为奇数函数,且 如果u和v分别是方程(1)具有局部齐次边界值(6)和不同的初值u0(x)、v0(x)的两个弱解,可以选择Sn(φ(u-v))作为检验函数,则 φu-v)· (11) 于是, (12) (13) (14) 而由于bi(s)是Lipschitz函数,|g(x)|≤cρ(x),|bi(u)-bi(v)|≤c|u-v|。根据迹的定义,容易推导出 (15) 此外,同文献[11],可以证明 (16) 具体如下 (17) 如果{x∈Ω:|u-v|=0}是0测度的集合,则 如果集合{x∈Ω:|u-v|=0}有正测度,则 因此,在这两种情况下,当η→0时,式(17)趋于0。 其次, (18) 对于任意固定的s,τ∈[0,T),通过取极限,可以选择χ[τ,s](u-v)φ作为检验函数,其中χ[τ,s]是[τ,s]上的特征函数,φ(x)由文献[10]定义,有: ∬Qτsg(x)[bi(u)-bi(v)][(u-v)φ]xidxdt-∬Qτs[bi(u)-bi(v)]gxiφ(u-v)dxdt, (19) 其中Qτs=Ω×[τ,s]。 可以把式(19)重新整理得到: 2∬Qτsg(x)[bi(u)-bi(v)][(u-v)φ]xidxdt-∬Qτs[bi(u)-bi(v)]gxiφ(u-v)dxdt≤ 2∬Qτsg(x)[bi(u)-bi(v)][(u-v)φ]xidxdt-∬Qτs[bi(u)-bi(v)]gxiφ(u-v)dxdt。 (20) 首先,因为 (21) 由α>p+-1和α-p(x)>-1及式(21)得 (22) 其次, ∬Qτsg(x)[bi(u)-bi(v)][(u-v)φ]xidxdt=∬Qτsg(x)[bi(u)-bi(v)][(u-v)φxi+(u-v)xiφ]dxdt。 由于|ρxi|≤|ρ|=1,根据式(9),|g(x)|≤cρ(x),则: (23) 这里u,v∈L∞(QT),根据式(9),|g(x)|≤cρβ(x)及β≥α/p-,有 |∬Qτsg(x)[bi(u)-bi(v)](u-v)xiφdxdt|≤ (24) 根据引理1的ⅲ),p1=p+或p-,q1=maxp(x)/(p(x)-1)或minp(x)/(p(x)-1)。 令Ω1={x∈Ω:p(x)/(p(x)-1)≥2},Ω2={x∈Ω:p(x)/(p(x)-1)<2},则 (25) 且 (26) 其中q2=max 2(p(x)-1)/p(x)或min 2(p(x)-1)/p(x)是根据引理1的ⅲ)来确定。 结合式(24)~式(26),得到 (27) 其中l<1。 还有, (28) 在式(20)中让λ→0,由式(22)~式(23)及式(27)~式(28),可得 (29)


3 定理1和定理2的证明
3.1 定理1的证明

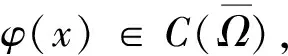
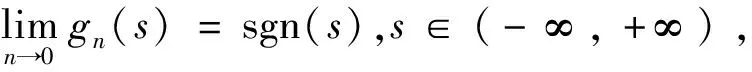
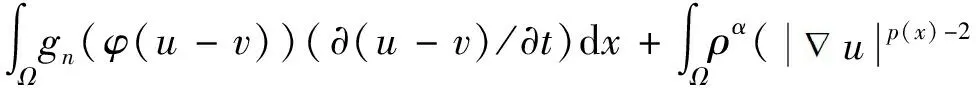

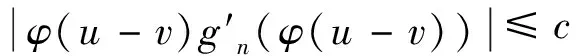


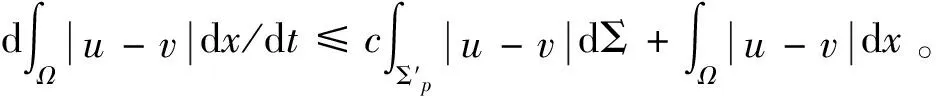
3.2 定理2的证明