可满着色图的一种结构

赵小玲

(上海电机学院 文理学院, 上海 201306)

对于可满着色图，吕长虹等[7]进行了一些深入研究，证明了以下的结论。

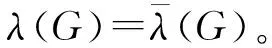
1 理论基础

对于一般图的广义Mycielski图，首先给出如下定义：

定义1G=(V,E)是一个简单图，|G|=n,V(G)={v01,v02,…,v0n}，p≥2为给定的整数，Mp(G)称为图G广义Mycielski图，如果满足:

V(Mp(G))={v01,v02,…,v0n,v11,v12,…,

v1n,…,vp1,vp2,…,vpn}

E(Mp(G))=E(G)∪{vijv(i+1)k|v0jv0k∈E(G),

1≤j,k≤n,i=0,1,…,p-1}

下面讨论一般图的广义Mycielski图的连续标号问题。下述定理可以说明连续标号的性质。

引理3[3]对于任意n阶的图G，下列命题是等价的:

(1)图G具有连续标号。

(2)G的补图中具有Hamilton路。

引理4[7]令Mp(Kn)是Kn的广义Mycielski图，则

2 主要结论

定理1对于任意的图G，Mp(G)一定具有连续标号。

由广义Mycielski图的定义，可以得到广义Mycielski图Mp(G)的补图Mp(G)C的结构:

结论1令Ai={vi1,vi2,…,vin}(i=0,1,…,p)，则A0的生成子图是GC，其他Ai(i=1,2,…,p)的生成子图都是完全图Kn。

结论2vijv(i+1)j∈E(Mp(G)C),(i=0,1,…,p-1;j=1,2,…,n)。

结论3若v0jv0k∈E(Mp(G)C)，则

vijv(i+1)k∈E(Mp(G)C)，

(i=0,1,…,p-1;1≤j,k≤n)

由此，得到定理1的证明:

情况1当GC中有一条Hamilton路，不妨设为v01v02…v0n。则可以用如下方法找到Mp(G)C的一条Hamilton路:

(1)当p为偶数时，这条Hamilton路为

v01v02…v0n→v1nv1(n-1)…v11→

v21v22…v2n→……→vp1vp2…vpn

(2)当p为奇数时，这条Hamilton路为

v01v02…v0n→v1nv1(n-1)…v11→

v21v22…v2n→……→vpnvp(n-1)…vp1

情况2当GC的路覆盖数为r(r≥2)，这r条路分别为P1,P2,…,Pr，设P1为v01v02…v0n1，P2为v0(n1+1)v0(n1+2)…v0(n1+n2)，…，

Pr为v0(n1+n2+…+nr-1+1)v0(n1+n2+…+nr-1+2)…

v0(n1+n2+…+nr-1+nr)。其中

n1+n2+…+nr-1+nr=n

则可以用如下方法找到Mp(G)C的一条Hamilton路:

v0n1v0(n1-1)…v01→v11v12…v1n1v1(n1+1)

→v0(n1+1)v0(n1+2)…v0(n1+n2)→v1(n1+n2)v1(n1+n2+1)

→v0(n1+n2+1)v0(n1+n2+2)…v0(n1+n2+n3)→…

→v0(n1+n2+…+nr-1+1)v0(n1+n2+…+nr-1+2)…

v0(n1+n2+…+nr-1+nr)v1(n1+n2+…+nr-1+nr)

→v2(n1+n2+…+nr-1+nr)v2(n1+n2+…+nr-1+nr-1)…v22v21

→v31v32…v3(n1+n2+…+nr-1+nr-1)v3(n1+n2+…+nr-1+nr)

→v4(n1+n2+…+nr-1+nr)v4(n1+n2+…+nr-1+nr-1)…v42v41

→…

(当p为奇数时)→vp1vp2…

vp(n1+n2+…+nr-1+nr-1)vp(n1+n2+…+nr-1+nr)。

(当p为偶数时)→vp(n1+n2+…+nr-1+nr)

vp(n1+n2+…+nr-1+nr-1)…vp2vp1。

对任意图G，沿着Mp(G)C的该Hamilton路的轨迹进行标号，由引理3，Mp(G)一定有一个连续的L(2,1)标号。

证毕。

由广义Mycielski图的定义，可得到广义Mycielski图Mp(G)的如下一些结构特征:

结论4令Ai={vi1,vi2,…,vin}(i=0,1,…,p)，则A0的生成子图是G，其他Ai(i=1,2,…,p)的生成子图都是独立集。

结论5dMp(G)(vijv(i+1)j)≥3,(i=1,…,p-1;j=1,2,…,n)，dMp(G)(vijv(i+m)j)≥m,(i=0,1,…,p-m;j=1,2,…,n;m≥2)。

定理2的证明当p=2时，观察图G的二串广义Mycielski图M2(G)。假设图G的顶点集为A0，M2(G)的第1串和第2串的顶点集分别为A1、A2，显然，A0的生成子图即为G。记A0∪A1的生成子图为G′，A0∪A1∪A2的生成子图为G″。

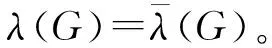
当p≥3时，由结论5

dMp(G)(vijv(i+3)j)≥3

(i=0,1,…,p-3;j,k=1,2,…,n)

证毕。