DYNAMIC FOR A STOCHASTIC MULTI-GROUP AIDS MODEL WITH SATURATED INCIDENCE RATE*
2021-01-07QixingHAN韩七星
Qixing HAN (韩七星)
School of Mathematics, Changchun Normal University, Changchun 130032, China School of Mathematics, Jilin University, Changchun 130012, China E-mail : hanqixing123@163.com
Daqing JIANG (蒋达清)†
Nonlinear Analysis and Applied Mathematics (NAAM)-Research Group, Department of Mathematics,King Abdulaziz University, Jeddah, Saudi Arabia College of Science, China University of Petroleum (East China), Qingdao 266580, China E-mail : daqingjiang2010@hotmail.com

The AIDS population is often divided into three parts:the susceptible population(S),the infected population(I),and the AIDS patient population(A).Here,Iis subdivided intongroupsI1,I2,···,In.We all know that incidence rate plays an important role in modelling epidemics.Some authors employ the bilinear incidence rateβSI[6,7].The classical deterministic multi-group AIDS epidemic model with bilinear incidence rate is described by the followingn+2 dimensional ODE:
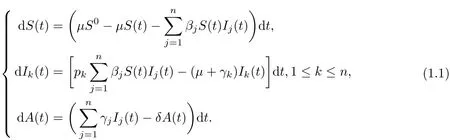
HereS(t)denotes the density of the population of susceptible individuals at timet,Ik(t)is the density of HIV-infected individuals in thek-th group at timet,andA(t)is the density of AIDS patients at timet.
The quantitiesS0,µ,βk,pk,γk,δare defined as follows:
S0:a constant steady state of the susceptible populationS.
µ:the rate of inflow and outflow.

Capasso and Serio[10]introduced a saturated incidence rateinto epidemic models in 1978,whereβImeasures the infection force of the disease,and 1+αImeasures the inhibition effect owing to the crowding of the infective;hereαis a positive constant.In fact,the real world is full of stochasticity[11–17].The transmission of diseases are always affected by environmental noise which can provide an additional degree of realism when compared to deterministic counterparts.In[18],Dalal,Greenhalgh and Mao considered the effect of environmental stochasticity in a model of AIDS,and found that the introduction of stochastic noise may change the basic reproduction number of the disease and stabilize an otherwise unstable system.Ding et al.[19]discussed a stochastic model for AIDS,studying two kinds of stabilities:almost surely exponential stability,and pth moment exponential stability.Liu et al.[20]proposed a stochastically perturbed DI SIR epidemic model with saturated incidences,and the asymptotic behavior of the stochastic model was obtained.Liu and Jiang[21]studied stochastic multigroup S-DI-A epidemic models for the transmission of HIV,obtaining sufficient conditions for the existence of a unique ergodic stationary distribution of the positive solutions and sufficient conditions for exponential extinction of the system with regime switching.Research on the stochastic model of AIDS has become much more popular and important on recent times,and the research in this area is still going on.
In this paper,we will focus on a reasonable analogue of system(1.1),that is,the multigroup AIDS epidemic model with saturated incidence rate and white noise.We get the following stochastic system:

2 Preliminaries


3 Persistence in the Mean
In this section,we will discuss the persistence of system(1.3),which demonstrates that the disease will be permanent under some conditions.



4 Existence of Stationary Distribution



Then (4.16), together with (4.10), yields LV <−1.
According to the discussion above,we have LV < −1 for any(S,I1,I2,··· ,In)∈U.Hence condition A2in Lemma 2.1 is satisfied. In addition, choosing
where ξ = (ξ0,ξ1,··· ,ξn). This means that condition A1is satisfied. By Lemma 2.1, the desired results can be derived.
Remark 4.2In Ref [20], Liu and Yang investigated the asymptotic behavior of system(1.3). They showed that the system is ergodic and converges weakly to the unique invariant distribution provided that the following conditions hold:
(H1) R0>1, σs>0,σi>0,i=1,2,··· ,n;
(H2)

where E∗= (S∗,,I2,··· ,In) is the interior equilibrium of the deterministic system (1.1).The existence of stationary distribution depends heavily on the positive equilibrium of the corresponding deterministic system. Theorem 4.1 in our investigation shows that the condition for the existence of the invariant distribution of system (1.3) is R∗> 1, without any other conditions imposed on the coefficients. Therefore, Theorem 4.1 greatly improves Theorem 4.2 in [20].
5 Numerical Simulation
In this section, we will perform some numerical simulations to illustrate our theoretical results. We simulate the solution of system (1.3) with k =2. By using Milstein’s higher-order method [26], we obtain the following discretization system:

where ε1,k, ε21,kand ε22,kare N(0,1)-distributed independent Gaussian random variables. We take parameters of the system as S0= 2,µ = 0.3,β1= 0.3,β2= 0.4,α1= 1,α2= 1, γ1= 0.1,γ2=0.2,p1=0.4,p2=0.6,σs=0.1,σ1=0.1,σ2=0.1.In this case,

so the condition in Theorem 4.1 is satisfied.Theorem 4.1 indicates that there is a stationary distribution for system(1.3).Fig.1 confirms this conclusion.

Fig.1 Left:the solutions of the stochastic system(red)and the corresponding deterministic system(blue).Right:the density functions the solutions.
6 Conclusion
Research on AIDS models that incorporates environmental noise and different incidence rates is becoming one of the important areas in the mathematical theory of epidemiology.In this paper,we present a stochastic AIDS epidemic model with a saturated incidence rate to describe the transmission of HIV/AIDS.With the help of a stochastic Lyapunov analysis method,we obtain the sufficient conditions for persistence in the mean,and further show that if1,there is an ergodic stationary distribution for the system.Our results indicate that the existence of an ergodic stationary distribution does not rely on the interior equilibrium of the corresponding deterministic system,which improves upon previous results.We also note that ifαj=0,j=1,2,···,n,system(1.3)is the stochastic version of system(1.1).ComparingR0withR∗,we obtain thatR∗
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- ITˆO DIFFERENTIAL REPRESENTATION OF SINGULAR STOCHASTIC VOLTERRA INTEGRAL EQUATIONS∗
- ON THE NUCLEARITY OF COMPLETELY 1-SUMMING MAPPING SPACES*
- EXISTENCE AND UNIQUENESS OF THE POSITIVE STEADY STATE SOLUTION FOR A LTKA-VTE PEDPY MD WIH CING*
- ASYMPTOTICS OF THE CROSS-VARIATION OF YOUNG INTEGRALS WITH RESPECT TO A GENERAL SELF-SIMILAR GAUSSIAN PROCESS∗
- THE DECAY ESTIMATES FOR MAGNETOHYDRODYNAMIC EQUATIONS WITH COULOMB FORCE*
- VAR AND CTE BASED OPTIMAL REINSURANCE FROM A REINSURER'S PERSPECTIVE*
