EXISTENCE AND MULTIPLICITY OF SOLUTIONS FOR A COUPLED SYSTEM OF KIRCHHOFF TYPE EQUATIONS∗
2021-01-07YaghoubJALILIAN
Yaghoub JALILIAN
Department of Mathematics,Razi University,Kermanshah,Iran
E-mail:y.jalilian@razi.ac.ir
Abstract In this paper,we study the coupled system of Kirchhoff type equationswhere a,b>0,α,β>1 and 3<α+β<6.We prove the existence of a ground state solution for the above problem in which the nonlinearity is not 4-superlinear at infinity.Also,using a discreetness property of Palais-Smale sequences and the Krasnoselkii genus method,we obtain the existence of infinitely many geometrically distinct solutions in the case when α,β≥2 and 4≤α+β<6.
Key words Kirchhoff equation;Nehari-Poho˘zave manifold;constrained minimization;ground state solution
1 Introduction
In this article,we investigate the existence and multiplicity of solutions to the coupled system of Kirchhoff type equations
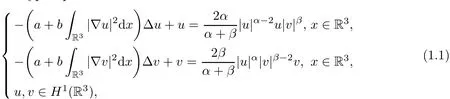
wherea,b>0,α,β>1 and 3<α+β<6.
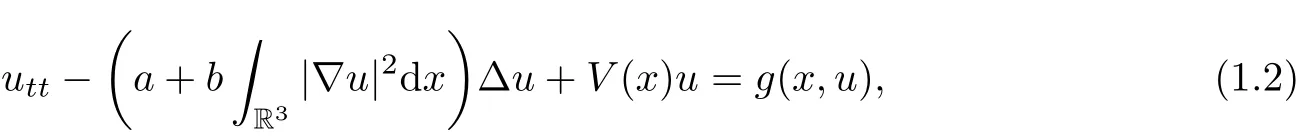
Kirchhoff type equations are related to the stationary analogue of the equation proposed by Kirchhoff[1]which is an extension of the classical D’Alembert’s wave equation for free transversal vibrations of a clamped string.Equation(1.2)arises in various physical and biological systems.For example,in biological systems,ucould describe the population density in a biological phenomena such as bacteria spreading(see[2]).

The assumptions considered in[5]imply the Cerami compactness condition for the energy functional.As far as we know[5]is the only paper considering the existence of infinitely many solutions for(1.3)in whichf(x,u)may not be 4-superlinear at infinity.To the best of our knowledge,there are a few results concerning the existence of solutions for coupled Kirchhoff type systems.Shi and Chen[16]investigated the existence of a ground state solution for the system
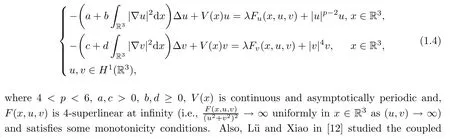
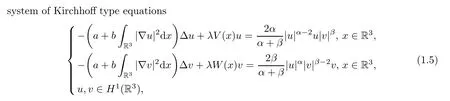
wherea,b>0,λ>0 is a real parameter,α>2,β>2,α+β<6 andV(x),W(x)are nonnegative continuous functions on R3.They established the existence and multiplicity of solutions to(1.5)forλ>λ0>0.In this paper,the assumption 4<α+βis crucial to prove the boundedness of Palais-Smale sequences.This assumption implies the 4-superlinearity of the nonlinearity at infinity.Therefore,the results of[12,16]are not applicable for(1.1)when 3<α+β≤4.
The aim of this paper is to prove the existence of a ground state solution to the coupled Kirchhoff type system(1.1)when 3<α+β<6.We use an argument developed by[11],to obtain a natural constraint via the Nehari manifold and the Poho˘zave identity.Moreover,using the Krasnoselskii genus,we investigate the existence of infinitely many geometrically distinct solutions in the case whenα,β≥2 and 4≤α+β<6.
In our first main result we prove the existence of a ground state solution for(1.1).
Theorem 1.1Assumeα,β>1 and 3<α+β<6.Then problem(1.1)has a ground state solution.
In our next result we study the multiplicity of solutions for(1.1).Letw=(u,v)be a solution of(1.1).Define the orbit ofwunder the action of Z3as O(w):={w(·−k):k∈Z3}.Two solutionsw1andw2are said to be geometrically distinct if O(w1)and O(w2)are disjoint.
Theorem 1.2Letα,β≥2 and 4≤α+β<6.Then problem(1.1)has infinitely many geometrically distinct solutions.
NotationsC,C1,C2,···are positive constants.B(r,x):={y∈R3:|x−y| We also recall the definition of the Krasnoselskii genus[19].A setF⊂Xis said to be symmetric ifF=−F.Let ForF≠∅andF∈Σ,the Krasnoselskii genus ofFis the least integernsuch that there exists an odd functionf∈C(F,Rn{0}).The genus ofFis denoted byγ(F).Setγ(∅):=0 andγ(F):=∞if there exists nofwith the above property for anyn. According to Theorem 1.1 the setKis nonempty.Let G be a subset ofKsuch that G=−G and each orbit O(u)⊂Khas a unique representative in G.We shall show that G has infinitely many elements.In the sequel,by contradiction,we assume that G is a finite set and this will lead to a contradiction. Lemma 4.1κ:=inf{‖v−w‖:v,w∈K∪{0},v≠w}>0. ProofThe proof is exactly the same as Lemma 2.13 in[20]and we omit it.We have to mention that in[20]the infimum is taken over allv,w∈K.Since 0 is an isolated critical point,κremains positive.2 Nehari-Poho˘zave Manifold










4 Proof of Theorem 1.2

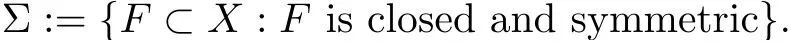






杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- CONTINUITY PROPERTIES FOR BORN-JORDAN OPERATORS WITH SYMBOLS IN H¨ORMANDER CLASSES AND MODULATION SPACES∗
- ASYMPTOTIC STABILITY OF A BOUNDARY LAYER AND RAREFACTION WAVE FOR THE OUTFLOW PROBLEM OF THE HEAT-CONDUCTIVE IEAL GAS WH SY*
- ON REFINEMENT OF THE COEFFICIENT INEQUALITIES FOR A SUBCLASS OF QUASI-CONVEX MPPG RL L RB*
- EXISTENCE OF SOULUTIONS FOR THE FRACTIONAL (p,q)-LAOLACIAN PROBLEMS INVOLVING A CRITICL SOBLEV EXPNN*
- RADIALLY SYMMETRIC SOLUTIONS FOR QUASILINEAR ELLIPTIC EQUATIONS INVOLVING NONHOMOGENEOUS OPERATORS IN AN ORLICZ-SOBOLEV SPACE SETTING∗
- ON VORTEX ALIGNMENT AND THE BOUNDEDNESS OF TH Lq-NORM OF VIRUICITY IN INCOMPRESSBLE VU FUD*
