RADIALLY SYMMETRIC SOLUTIONS FOR QUASILINEAR ELLIPTIC EQUATIONS INVOLVING NONHOMOGENEOUS OPERATORS IN AN ORLICZ-SOBOLEV SPACE SETTING∗
2021-01-07JaeMyoungKIM
Jae-Myoung KIM
Department of Mathematics Education,Andong National University,
Andong 36729,Republic of Korea E-mail:jmkim02@andong.ac.kr
Yun-Ho KIM†
Department of Mathematics Education,Sangmyung University,Seoul 03016,Republic of Korea
E-mail:kyh1213@smu.ac.kr
Jongrak LEE
Department of Mathematics,Jeju National University,Jeju 63243,Republic of Korea
E-mail:jrlee@jejunu.ac.kr
Abstract We investigate the following elliptic equations:where N≥2,1 Key words radial solution;quasilinear elliptic equations;variational methods,Orlicz-Sobolev spaces In recent years,great attention has been paid to the study of certain nonlinear equations,including non-homogeneous operators of the type The interest in such operators has consistently increased in light of the relevence of the pure or applied mathematical theory to some concrete phenomena,such as nonlinear elasticity,fluid mechanics,plasticity theory,biophysics problems,and plasma physics;see[22–25,28]and the references therein.In the case of nonlinear quasilinear elliptic equations,a functional setting is achieved by using Sobolev spaces to treat the problem variationally.In contrast,the study of nonhomogeneous differential operators is based on the theory of Orlicz-Sobolev spaces.In this direction,variational problems for elliptic equations of this type have been widely studied in recent years;for example,see[1,2,10,13–15,18–20,26,27,37,43,44,46],and see[8,11,47,56]for problems with variable exponents.We also refer the reader to[21,40,41,53,54]for further reading on the existence and multiplicity results for nonlocal problems. The interest of the present paper in analyzing problems involving nonhomogeneous operators in divergence form is motivated by the recent works of Azzollini et al.[5,6].Employing the mountain pass theorem and its Z2-symmetric version,the authors in[6]dealt with the existence and multiplicity of non-negative radially symmetric solutions for problems associated with a new class of differential operators in an Orlicz-Sobolev space whenφhas a different behavior near zero and at infinity;for instance, As noted in[6],the theory of classical Sobolev spaces is not applicable,because the different growth of the principal part and an unbounded domain are considered.Thus,in order to obtain the existence results,the authors of[6]introduced an adequate functional framework based on the paper[7].This approach to the sum of Lebesgue spaces is new and different from the previous related works[1,2,10,14,15,20,26,27,37],although the functional setting is considered in an Orlicz-Sobolev space.Inspired by the results in[5,6],Chorfi and R˘adulescu[12]obtained the result that the quasilinear Schr¨odinger equation, possesses at least one nontrivial solution where the potential functionais singular.For this,the mountain pass theorem has been employed which is originally proposed by the paper[4],and it is a basic tool in looking for solutions to elliptic equations of variational type.In particular,the authors of[4]ensured the boundedness of the Palais–Smale sequence of the Euler-Lagrange functional when the nonlinear termfsatisfies the Ambrosetti and Rabinowitz condition(AR condition).Even if this condition onfis somewhat natural and essential in guaranteeing the compactness condition of the Euler-Lagrange functional,it is very limited and removes many nonlinearities.For this reason,many authors have tried to eliminate the AR condition for elliptic equations involving thep-Laplacian;see[33–36,39].Liu[34]obtained the existence result of solutions for thep-Laplacian equation under the following assumption: (f)There existsη≥1 such that The condition above was initially proposed by Jeanjean[29]in the case ofp=2.In the last few decades,there were extensive studies dealing withp-Laplacian problems by assumption(f);see[33,35]for thep-Laplacian and[3,30,55]for thep(x)-Laplacian.In particular,the authors of[33]provided many examples that did not fulfill the condition of the nonlinear termhgiven in[3,34–36,55];for instance, wherem∈C(RN,R)and 0 This paper is devoted to the study of the existence of radially symmetric solutions for the following quasilinear elliptic equations with general nonlinearities in Orlicz-Sobolev spaces: whereφandMwill be specified later,h:RN×R→R is a Carath´eodory function andh(·,u)is radial.The primary tools for obtaining our results are the mountain pass theorem and the fountain theorem under the Cerami condition,which is slightly weaker than the well-known Palais–Smale condition.As we know,the boundedness of a sequence of the Palais–Smale type plays a central role in applying these theorems.However,in comparison with[3,6,12,33–35],it is difficult to obtain this compactness condition because the Kirchhoff functionMis not convex and our function space is an Orlicz-Sobolev space,which is endowed with the sum of weighted Lebesgue spaces. The first aim of this paper is to present the existence of at least one nontrivial radially symmetric solution for our problem when the condition forhhas mild and different assumptions from the condition on(f),which comes from[33].Second,we obtain the multiplicity of largeenergy radially symmetric solutions for problem(1.1)by employing the fountain theorem instead of the symmetric mountain theorem,which is a key tool for obtaining the multiplicity results in[6].Finally,considering the dual fountain theorem,we guarantee that our problem admits a sequence of small-energy radially symmetric solutions.Such multiplicity results for nonlinear elliptic equations of variational type can be found on[16,51],and the references therein.To the best of our knowledge,the present paper is the first to study the existence of multiple largeor small-energy solutions for our problem with the Kirchhoff functionM(even ifM≡1),the different growth conditions onφand the various conditions onh. The remainder of this paper is organized as follows:in Section 2,we review the well-known facts for the sum of Lebesgue spaces and Orlicz-Sobolev spaces.Based on this background,we show that there exist nontrivial weak solutions to the problem(1.1)under various conditions onh,using the mountain pass theorem.In Section 3,we prove the multiplicity result of nontrivial large-and small-energy radially symmetric solutions to problem(1.1)via the fountain lemma and the dual fountain theorem,respectively. In this section,we study some definitions and essential properties of the sum of Lebesgue spaces and an Orlicz-Sobolev space.We show the existence of nontrivial weak solutions to our problem using this background.For a deeper treatment of these spaces,we refer to[1,48].For simplicity,C is used to represent a generic constant,which may change from line,to line unless otherwise noted. Accounting to the convexity and continuity ofΦ,we can apply the same technique as in the proof of Proposition 3.3 in[6]to obtain that∇vn→∇vinLp(RN)+Lq(RN)asn→∞.With this fact,along with(2.18),we finally obtainvn→vstrongly in Wr. Next,under assumption(F6)instead of(F5),we show that Jλ|Wrsatisfies the Cerami condition. Lemma 2.15Assume that(F1),(F2),(F4),and(F6)hold.Then,the functional Jλ|Wrsatisfies the(C)c-condition for anyλ>0. ProofForc∈R,let{un}be a(C)c-sequence in Wrwith(2.2).Then,the relation(2.3)holds.As in the proof of Lemma 2.14,we only prove that{un}is bounded in Wr.To this end,arguing by contradiction,suppose that||un||W>1 and||un||W→∞asn→∞.Letvn=un/||un||W.Then,||vn||W=1.In passing to the limit,we may assume thatvn⇀vasn→∞in Wr,thenvn→vinLs(RN),α which implies Hence,it follows from(2.22)thatv≠0.From the same argument as to that of Lemma 2.14,we can check the relations(2.6)–(2.8)and induce the relation(2.9).Therefore,we have a contradiction,and thus,{un}is bounded in Wr. Using Lemma 2.14,we prove a nontrivial weak solution for problem(1.1)under these assumptions. Theorem 2.16Assume that(F1)–(F5)hold.Then,problem(1.1)admits a nontrivial radially symmetric solution for allλ>0. ProofNote that Jλ(0)=0.By Lemmas 2.11 and 2.14,the energy functional Jλpossesses all conditions of the mountain pass theorem.Therefore,we can find a nontrivial critical pointuof Jλin Wr.By the principle of symmetric criticality[42],uis also a critical point of Jλin W.Therefore,uis a nontrivial radially symmetric solution of problem(1.1)for allλ>0. Using Lemma 2.15,we have the same consequence for our problem under assumption(F6). Theorem 2.17Assume that(F1)–(F4)and(F6)hold.Then,problem(1.1)has a nontrivial radially symmetric solution for allλ>0. ProofIf we apply Lemma 2.15,the proof is almost the same as in Theorem 2.16. In this section,we guarantee the existence of a sequence of infinitely many large or small radially symmetric solutions to problem(1.1).To do this,we employ the fountain theorem in[52,Theorem 3.6]and the dual fountain theorem as the primary tools. Proposition 3.1(Fountain Theorem[52,Theorem 3.6])Let X be a separable and reflexive Banach space.For anyc>0,letΘ∈C1(X,R)fulfill the(C)c-condition,and letΘ be even.If,for each sufficiently largek∈N,there existsρk>δk>0 such that the following conditions hold: (1)bk:=inf{Θ(u):u∈Zk,||u||X=δk}→∞ask→∞; (2)ak:=max{Θ(u):u∈Yk,||u||X=ρk}≤0,then the functionalΘhas an unbounded sequence of critical values. Using Proposition 3.1,we establish the existence of infinitely many nontrivial weak solutions. Theorem 3.2Assume that(F1)–(F2)and(F4)–(F5)hold.Ifh(x,−t)=−h(x,t)holds for all(x,t)∈RN×R,then for anyλ>0,problem(1.1)has a sequence of nontrivial radially symmetric solutions{vn}such that Jλ(vn)→∞asn→∞. Remark 3.3It is obvious from Proposition 2.5 in[6]that space W is a reflexive Banach space.To employ the fountain theorem,we need the separability of this space.To this end,define for allt≥0 and set which contradicts(3.1). Note by Remark 3.3 that W is a separable and reflexive Banach space.By Lemma 2.14,Jλ|Wrsatisfies the(C)c-condition for everyc>0 and is an even functional.Hence,we look for a sequence of nontrivial critical points{vn}of Jλin Wr,via Proposition 3.1.As in the proof of Theorem 2.16,{vn}is a sequence of nontrivial radially symmetric solutions for problem(1.1).This completes the proof. Remark 3.4In the assumption of Theorem 3.2,if we replace(F5)with(F6),then the problem(1.1)possesses a sequence of nontrivial radially symmetric solutions{vn}in Wr(RN)such that Jλ(vn)→∞asn→∞. Finally,considering the dual fountain theorem,which was initially provided in[9],we show the existence of multiple small-energy radially symmetric solutions to problem(1.1).1 Introduction



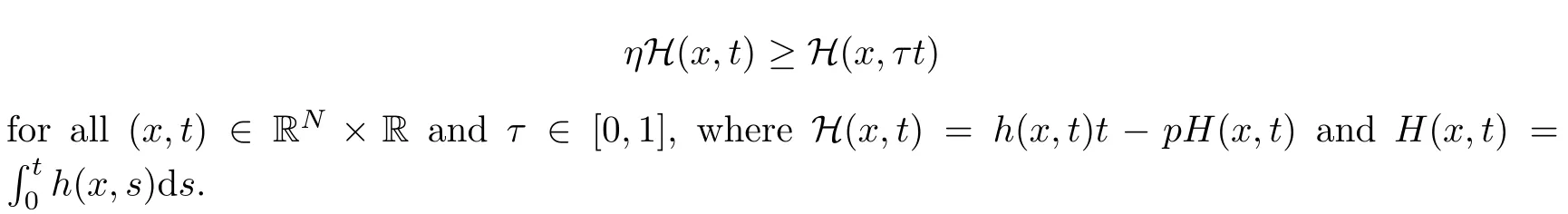
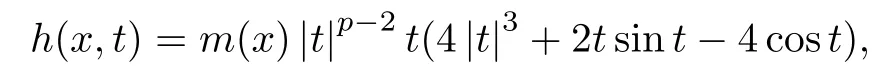

2 Preliminaries and Existence of a Weak Solution









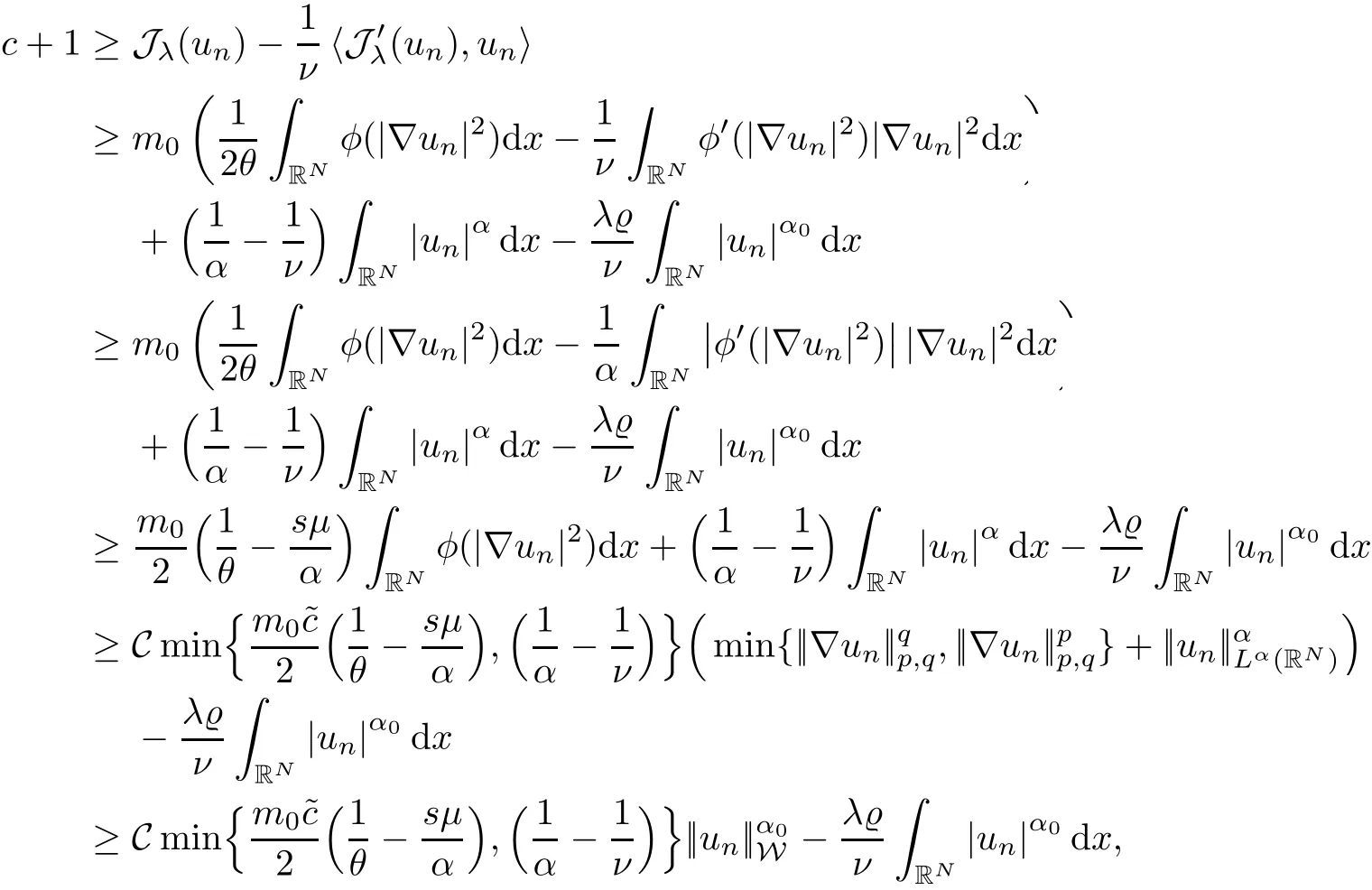
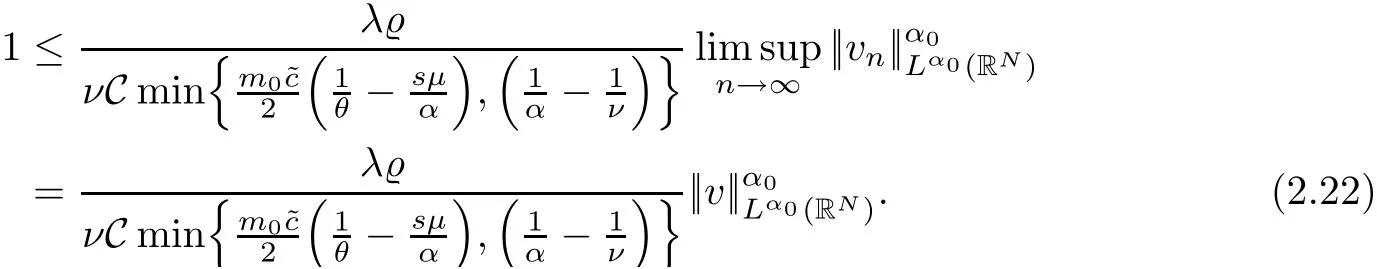
3 Existence of Infinitely Many Weak Solutions


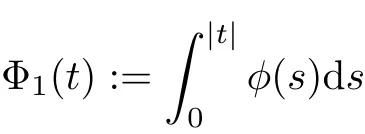





杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- ITˆO DIFFERENTIAL REPRESENTATION OF SINGULAR STOCHASTIC VOLTERRA INTEGRAL EQUATIONS∗
- ON THE NUCLEARITY OF COMPLETELY 1-SUMMING MAPPING SPACES*
- EXISTENCE AND UNIQUENESS OF THE POSITIVE STEADY STATE SOLUTION FOR A LTKA-VTE PEDPY MD WIH CING*
- ASYMPTOTICS OF THE CROSS-VARIATION OF YOUNG INTEGRALS WITH RESPECT TO A GENERAL SELF-SIMILAR GAUSSIAN PROCESS∗
- THE DECAY ESTIMATES FOR MAGNETOHYDRODYNAMIC EQUATIONS WITH COULOMB FORCE*
- VAR AND CTE BASED OPTIMAL REINSURANCE FROM A REINSURER'S PERSPECTIVE*
