CONTINUITY PROPERTIES FOR BORN-JORDAN OPERATORS WITH SYMBOLS IN H¨ORMANDER CLASSES AND MODULATION SPACES∗
2021-01-07MauricedeGOSSON
Maurice de GOSSON
Faculty of Mathematics,NuHAG,University of Vienna,Vienna,Austria
E-mail:maurice.degosson@gmail.com
Joachim TOFT†
Department of Mathematics,Linnæus University,V¨axj¨o,Sweden
E-mail:joachim.toft@lnu.se
Abstract We show that the Weyl symbol of a Born-Jordan operator is in the same class as the Born-Jordan symbol,when H¨ormander symbols and certain types of modulation spaces are used as symbol classes.We use these properties to carry over continuity,nuclearity and Schatten-von Neumann properties to the Born-Jordan calculus.
Key words quantization;Schatten-von Neumann;Feffermann-Phong’s inequality
1 Introduction
A fundamental question in quantum mechanics concerns quantization.That is,finding rules which takes observablesain classical mechanics into corresponding observablesTain quantum mechanics.Usuallyais a function of the locationx∈Rd(the configuration variable)and the momentumξ∈Rd,andTais a linear operator which acts between suitable Hilbert spaces of functions onRd.
The Born-Jordan quantization
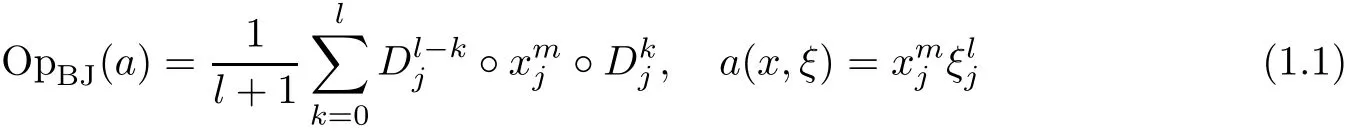
introduced in early days by Born and Jordan in[7],is nowadays considered as an important quantization rule(see e.g.[16–18]).(See also[30]and Section 2 for notations.)In a context of the calculus of pseudo-differential operators,Born-Jordan quantization is given by

where the symbola(x,ξ)is allowed to belong to more general classes compared to(1.1)(see Section 2 for details and notations).Here Opt(a)is the(t-Shubin)pseudo-differential operator with symbola,given by
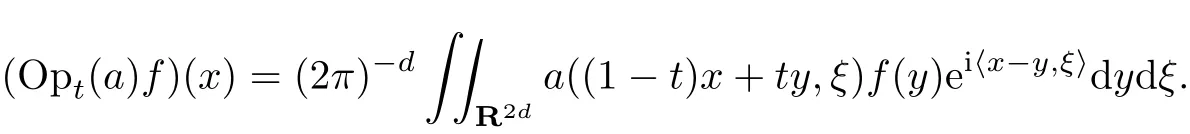
We have that Op0(a)=a(x,D)(i.e.,t=0)is the standard or Kohn-Nirenberg representation,and that Op1(a)(i.e.,t=1)is the adjoint representation.By choosingi.e.,the mean-value of these standard situations,we deduce the Weyl operator(or Weyl quantization)Opw(a)=Op1/2(a),given by
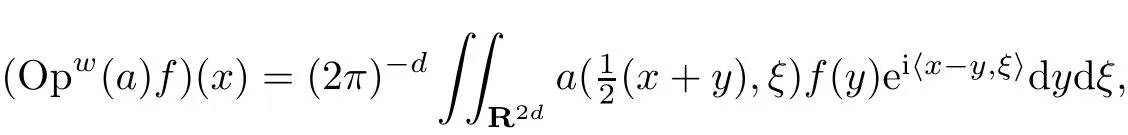
which is also considered as a suitable quantization rule.For example,among the operator representations above,only OpBJ(a)and Opw(a)possess the property to necessarily being self-adjoint(Hermit operators)whenais real-valued.
By using

the formula(1.2)becomes
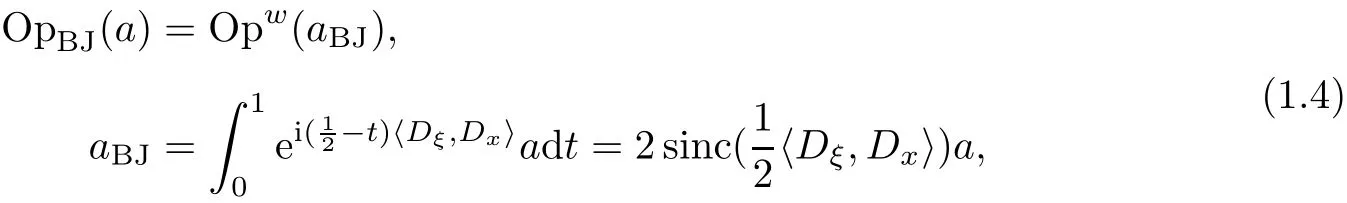
which puts the Born-Jordan quantization within the frame of the Weyl calculus of pseudodifferential operators.Here sinctis the sinc function,given by
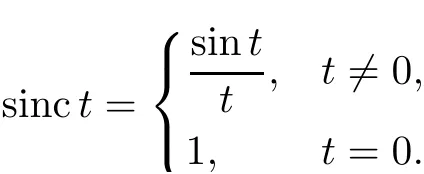
During the last 10 years,Born-Jordan quantization is also recognized in time-frequency analysis.In this field,time-frequency resolutions by Wigner distributions,i.e.,simultaneously localizations of the time and frequency for signals,are essential.A problem here concerns interpolating frequencies or so-called ghost frequencies,which originate from interference of existing frequencies but are absent in the signal,but are present in the graphs of their resolutions(see[4,5,48]).Especially we remark that in[48],Turunen showed that the time-frequency resolutions usually becomes significantly more clear when using Born-Jordan versionsWBJ(f,g)in place of classical time-frequency resolutions like the Wigner distributionsW(f,g).For example,it was shown in[48]that the ghost frequencies miraculously almost disappear when using suitable resolutions based on theWBJtransform.See also[14]for other related facts.
The impact of Born-Jordan operators in quantization and time-frequency analysis leads to questions on continuity for such operators.In quantization,it is suitable to consider general H¨ormander classesS(m,g)on the phase space.Recall thatS(m,g)agrees with classical symbol classes likeSG-classes or Shubin classes,by choosing the Riemannian metricgand the weight functionmin appropriate ways.In time-frequency analysis,it is suitable to use(classical)modulation spaces,as symbol classes,because they are especially adapted for energy estimates for time-frequency representations(cf.e.g.[38]).These spaces were introduced in[19]by Feichtinger and are obtained by imposing ancondition on the shorttime Fourier transform on the involved functions and(ultra-)distributions.(See also[20,22,25]and the references therein for more facts on modulation spaces.)
In Sections 3–6 we deduce several types of continuity properties for Born-Jordan operators.In similar way as in e.g.[11–13],the main idea is to use(1.2)to carry over continuity properties in pseudo-differential calculus to Born-Jordan operators.In Section 3 we consider Born-Jordan operators with symbols in the Schwartz space or in certain Gelfand-Shilov spaces and their duals.For example,we regain the fact from[11]that(1.2)leads to
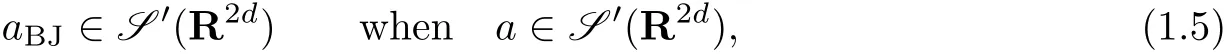
where S′(R2d)is the set of tempered distributions onR2d.(See Theorems 3.2 and 3.3.)In Section 3 it is proved that the same holds true with Ss(R2d),Σs(R2d)or their duals in place of S′(R2d),where Ss(Rd)(Σs(Rd))is the Fourier invariant Gelfand-Shilov space of Roumieu(Beurling)type of orders>0 onRd.In particular it follows that the following holds true:
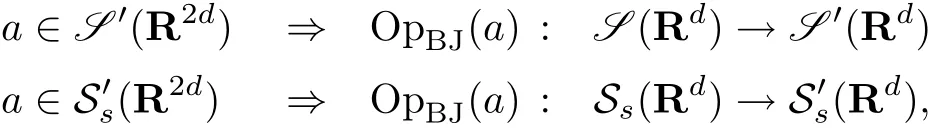
and
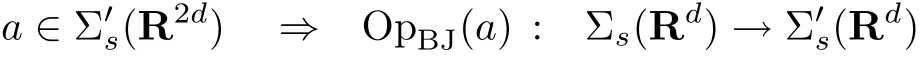
(whith continuous mappings),because the same continuity properties hold true with Opt(a)in place of OpBJ(a)for everyt.We remark that our investigations include more general Gelfand-Shilov spaces and their distributions,which do not need to be Fourier invariant(see Theorem 3.2).These properties give a solid basement of our investigations.
In Section 4 we consider Born-Jordan operators with symbols in modulation spaces,and prove that
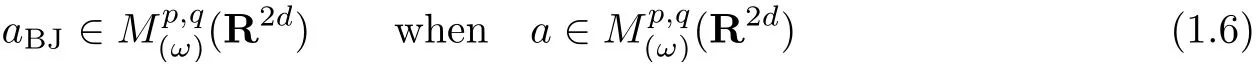
whenp,q∈(0,∞],provided the weightω(x,ξ,η,y)is constant with respect to thexandξvariables(see Theorem 4.1).It is well-known that for suchω,the map eit〈Dξ,Dx〉is continuous onfor everyt.(Cf.[46,Proposition 1.9].)In the special case whenp,q≥1,then(1.6)is deduced by a straight-forward combination of(1.2),(1.3)and Minkowski’s inequality.For such choices ofpandqand if all weights are trivially equal to one,then these investigations are related to those in[12].For example Theorem 4.3 in Section 4 overlaps with[12,Theorem 5.1].
In order to reach(1.6)in the general case,the possible lack of local-convexity of involved spaces,impose a more comprehensive analysis compared to the restricted casep,q≥1.In our approach,the symbolain(1.6)is expressed in terms of its Gabor expansion,using the fact that Gabor theory works properly for modulation spaces whenpandqare allowed to be smaller than 1.(Cf.[22,43].)By inserting such expansions in(1.2),(1.3)and performing some refined computations,we finally land on(1.6).
As a consequence of(1.6)we get,e.g.,

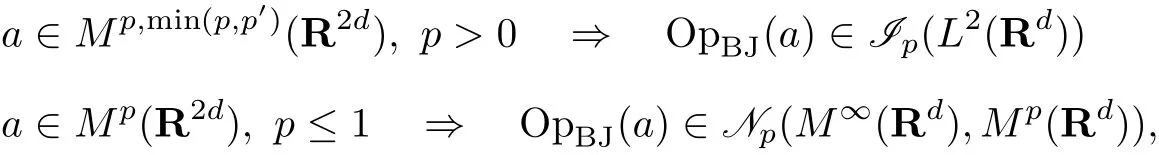
because the same hold true with Opt(a)in place of OpBJ(a)(cf.[45,46]).Herep′is the conjugate exponent ofp∈(0,∞],given by
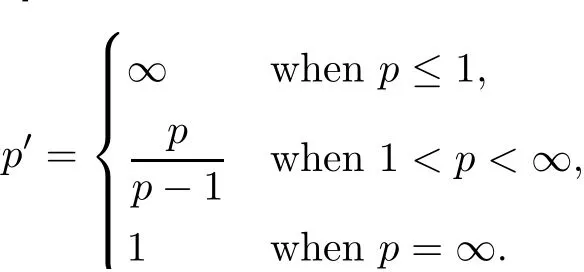
In Section 5 we deduce continuity properties for Born-Jordan operators with symbols in the(general)H¨ormander classS(m,g),wheregis a strongly feasible Riemannian metric andmis(σ,g)-temperated metric on the phase spaceR2d.We prove that if in additiongis split in the sensegX(y,−η)=gX(y,η),then
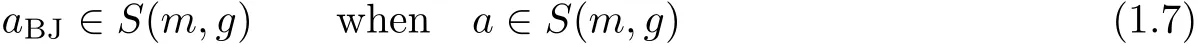
In particular,all continuity properties for pseudo-differential operators in[8,29,39,45]with symbols inS(m,g),carry over to Born-Jordan operators with symbols in the same class.In particular it follows that
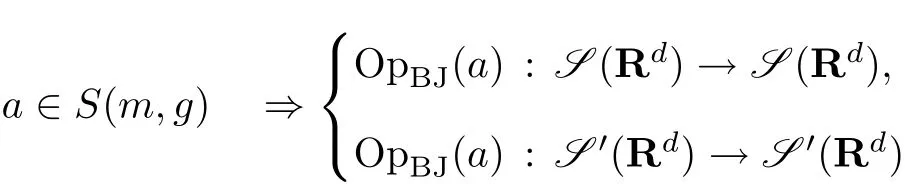
(see Theorem 5.4),and that
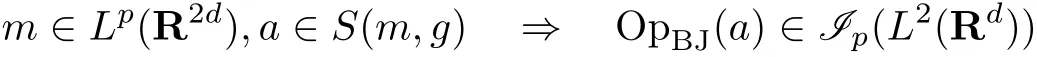
(see Theorems 5.6 and 5.7),because the same hold true with Opw(a)in place of OpBJ(a)(see[30,Theorem 18.6.2],[8,Theorem 2.9],[39,Theorem 4.4]and[45,Theorem 4.1]).
In the last part of Section 5 we deduce classical lower bound estimates for Born-Jordan operators.In fact,by asymptotic expansions it follows that ifa,aBJ∈S(m,g)satisfy(1.4),then

wherehgis the Planck’s function.This leads to that fundamental lower bound results carry over from the Weyl case to Born-Jordan case.In fact,Sharp G˚arding’s and Feffermann-Phong’s inequalities as well as H¨ormander’s improvement of Melin’s inequality,given by Theorems 18.6.7 and 18.6.8 in[30]and Theorem 6.2 in[28],are some of the most well-known lower bound results in pseudo-differential calculus.It follows from the small difference betweenaandaBJin view of(1.8)that these lower bound results carry over to Born-Jordan operators(see e.g.Theorem 5.9 in Section 5).
In Section 6 we consider Born-Jordan operators of so-called infinite orders.That is,in contrast to the H¨ormander classes,S(m,g),the involved symbols are allowed to grow faster than polynomials.On the other hand,it is assumed that the symbols obey stronger regularity conditions than what is required in the classS(m,g).We consider operators with symbols inconsidered in[1](see Definition 6.1 in Section 6).In[1]it is deduced that pseudo-differential operators with symbols in such classes are continuous on suitable Gelfand-Shilov spaces and their duals.In Section 6 we use(1.4)to carry over these continuity properties to Born-Jordan operators with symbols in
2 Preliminaries
In this section we start by recalling some facts about Gelfand-Shilov spaces of functions and distributions.Thereafter,we recall the definition of pseudo-differential operators and Born-Jordan operators.Some basic properties for Schatten-von Neumann and nuclear operator classes are then discussed in Subsection 2.3.We conclude the section by recalling some facts on modulation spaces.
2.1 Gelfand-Shilov spaces and their duals

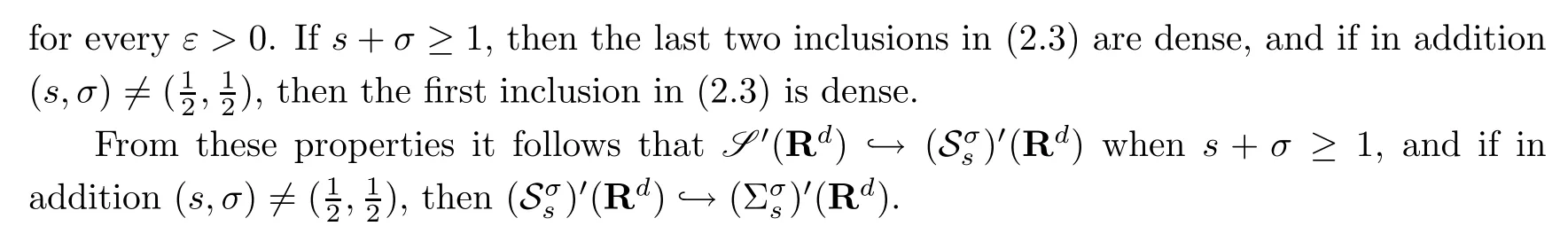
The Gelfand-Shilov spaces possess several convenient mapping properties.For example they are nuclear and invariant under translations,dilations,and to some extent tensor products and(partial)Fourier transformations(cf.[23,33,35]).

Next we recall some mapping properties of Gelfand-Shilov spaces under short-time Fourier transforms andt-Wigner distributions.Letφ∈S(Rd)be fixed.For everyt∈R,f∈S′(Rd),the short-time Fourier transformVφfis the distribution onR2ddefined by the formula
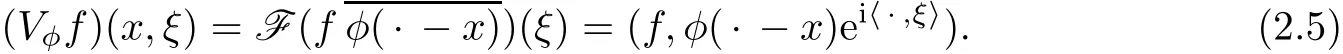
Thet-Wigner distribution is given by

We observe that iff,φ∈S(Rd),thenVφfandWt(f,φ)are given by
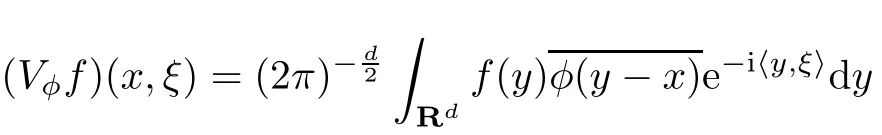
and
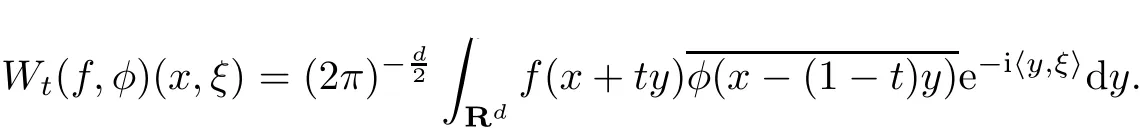
The definition of short-time Fourier transforms and Wigner distributions extend in different ways,and possess various kinds of continuity properties.In the context of test function spaces and distribution spaces we have the following.
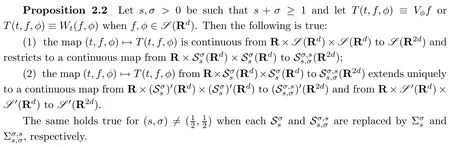
Proposition 2.2 is essentially available in the literature(see e.g.[15,41]).Since in contrast we have included the parametertas a variable,we here recall the arguments for thet-Wigner distribution.
ProofWe only prove(2).The other cases follow by similar arguments and are left for the reader.
By the definition we have
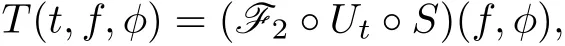
where
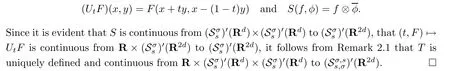
Remark 2.3By the previous proof it also follows that the mappings in Proposition 2.2 are locally uniformly bounded.
We also notice that ifTis the same as in Proposition 2.2,then the mappings
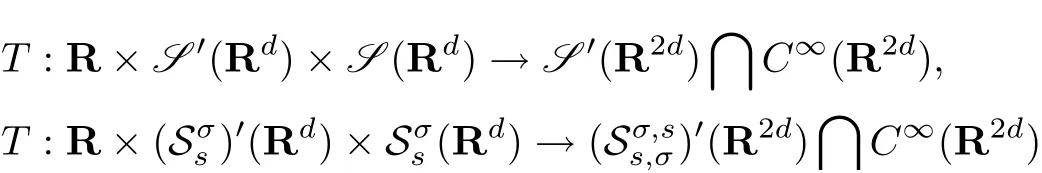
and

are continuous(cf.[1,15,41,44]).
There are several ways to characterize Gelfand-Shilov spaces and their distribution spaces.For example,they can easily be characterized by Hermite functions and other related functions(cf.e.g.[24,31,34,35]).They can also be characterized by suitable estimates of their Fourier and Short-time Fourier transforms(cf.[10,27,41,44]).
2.2 Pseudo-differential and Born-Jordan operators
Lett∈Rbe fixed.For anya∈S(R2d)(the symbol),the pseudo-differential operator Opt(a)is the linear and continuous operator on S(Rd),defined by
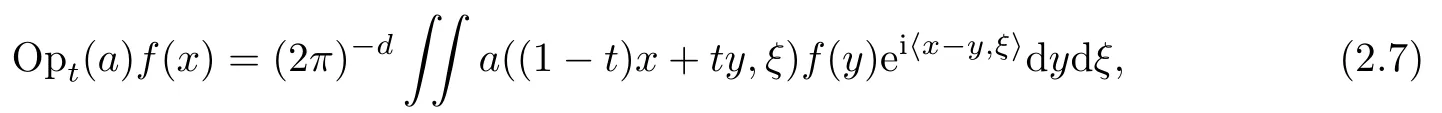
whenf∈S(Rd).By straight-forward computations it follows that

We recall that the Born-Jordan operator OpBJ(a)with symbolais given by(1.2).It follows from(2.8)that
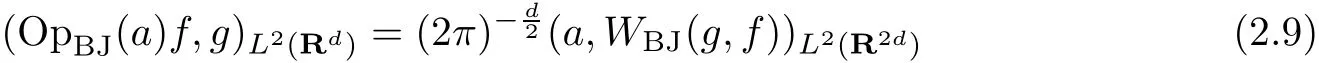
with

2.3 Schatten-von Neumann classes and nuclear operators
Before giving the general definition of Schatten-von Neumann classes we recall some facts on quasi-Banach spaces.A quasi-norm‖·‖B of orderr∈(0,1]on the vector-space B is a nonnegative functional on B which satisfies
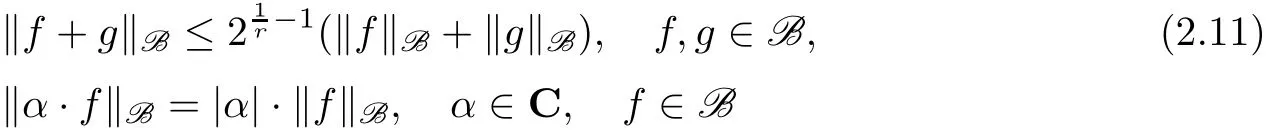
and

The vector space B is called a quasi-Banach space if it is a complete quasi-normed space.If B is a quasi-Banach space with quasi-norm satisfying the weak triangle inequality(2.11),then by[2,36]there is an equivalent quasi-norm towhich additionally satisfies
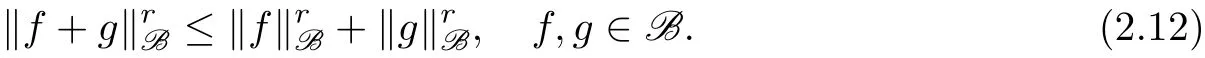
From now on we always assume that the quasi-norm of the quasi-Banach space B is chosen in such a way that both(2.11)and(2.12)hold.
Let B1and B2be(quasi-)Banach spaces and letTbe a linear operator from B1to B2.The singular value ofTof orderj≥1 is defined as
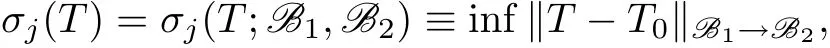
where the infimum is taken over all linear operatorsT0from B1to B2of rank at mostj−1.(Cf.e.g.[3,37,42].)The operatorTis said to be a Schatten-von Neumann operator of orderp∈(0,∞]if
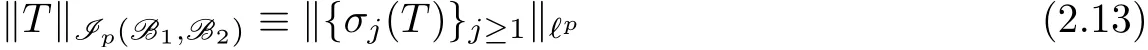
is finite.The set of Schatten-von Neumann operators from B1to B2of orderp∈(0,∞]is denoted by Ip(B1,B2).We observe that Ip(B1,B2)is contained in K(B1,B2),the set of compact operators from B1to B2,whenp<∞.Furthermore,I∞(B1,B2)agrees with B(B1,B2),the set of linear bounded operators from B1to B2.For conveniency we set I∞(B,B)=I∞(B).
Next we define nuclear operators.Let B0be a Banach space with dual,B be a quasi-Banach space,r∈(0,1]and letTbe a linear and continuous operator from B0to B.ThenTis calledr-nuclear from B0to B,if there are sequencesandsuch that

with convergence in B(B0,B),and

HereTin(2.14)should be interpreted as the operator
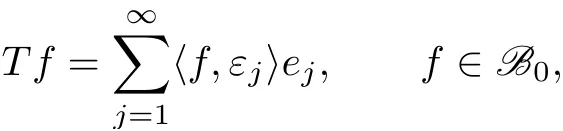
which is well-defined when(2.15)holds.The set ofr-nuclear operators from B0to B is denoted by Nr(B0,B),and we equip this set by the quasi-norm
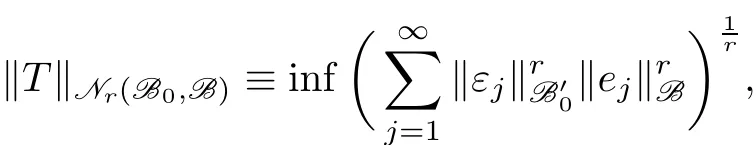
where the infimum is taken over all representatives⊆B such that(2.14)and(2.15)hold true.
Later on we need the following result which shows thatp-nuclearity is stable under linear continuous mappings.Here and in what follows we writeg≲hwheng(θ)≤ch(θ)for some constantc>0 which is independent ofθin the domains ofgandh.We also letg≍hwheng≲handh≲g.
Proposition 2.4Letp∈(0,∞],r∈(0,1],Bkbe quasi-Banach spaces of orderr,B0,kbe Banach spaces,Hkbe Hilbert spaces,k=1,2,and let
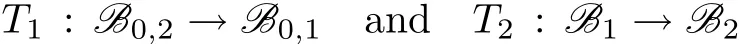
be continuous.Then the following is true:
(1)ifT∈Ip(B0,1,B1),thenT2◦T◦T1∈Ip(B0,2,B2),and
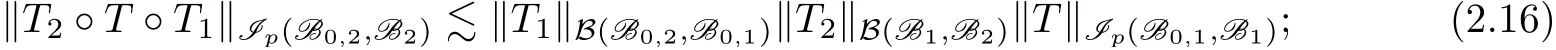
(2)ifT∈Nr(B0,1,B1),thenT2◦T◦T1∈Nr(B0,2,B2),and
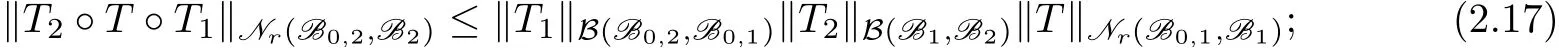
(3)Nr(H1,H2)=Ir(H1,H2),with equality in quasi-norms.
Proposition 2.4 is well-known in the literature(cf.[3,37,46]and the references therein).
2.4 Modulation spaces
Next we discuss basic properties for modulation spaces,and start by recalling the conditions for the involved weight functions.A functionωonRdis called a weight(onRd),ifω>0 andLetωandvbe weights onRd.Thenωis called moderate orv-moderate if
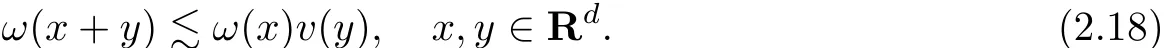
The weightvis called submultiplicative,ifvis even and(2.18)holds whenω=v.We note that if(2.18)holds,then
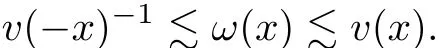
Furthermore,for suchωit follows that(2.18)is true when
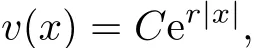
for some positive constantsrandC(cf.e.g.[26]).
The set of all moderate weights onRdis denoted by PE(Rd).

The proof of the following proposition is omitted,since the results can be found in[19–22,25].
Proposition 2.5Letp,q,pj,qj∈(0,∞]forj=1,2,r≤min(p,q,1),andω,ω1,ω2,v∈PE(R2d)be such thatvis submultiplicative,ωisv-moderate andω2≲ω1.Then the following is true:

3 Born-Jordan Operators with Distribution Symbols
In this section we deduce various kinds of mapping properties of OpBJ(a)whenabelongs to suitable test-function or distribution spaces.In particular we show that OpBJ(a)makes sense as a continuous operator from S(Rd)to S′(Rd)whena∈S′(R2d).
We begin with the following analogy of Proposition 2.2 in Born-Jordan situation.
Proposition 3.1Lets,σ>0 be such thats+σ≥1 and letT(f,φ)≡WBJ(f,φ)whenf,φ∈S(Rd).Then the following is true:
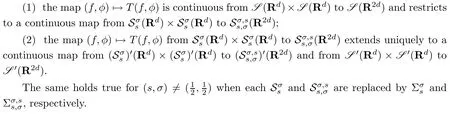
ProofWe use the same notations as in the proof of Proposition 2.2.We recall thatWBJ(f,g)is given by(2.9)whenf,g∈S(Rd).By Proposition 2.2 and Remark 2.3 it follows that the map(f,φ)|→WBJ(f,φ)is continuous from S(Rd)×S(Rd)to S(R2d),and that the same holds true if each S is replaced by Ssor byΣs.
In the same way,Proposition 2.2 and Remark 2.3 show that the map

where the last equality follows from the fact that
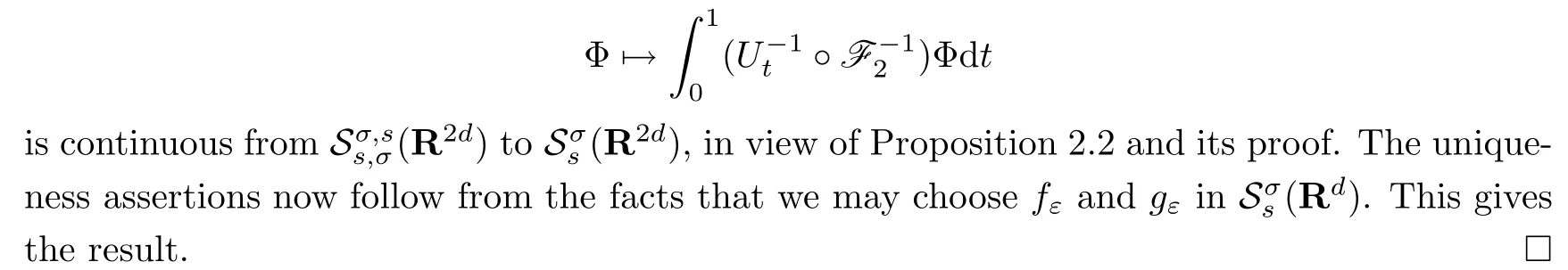
We have now the following.Here L(V1,V2)is the set of all linear and continuous mappings from the topological vector spaceV1into the topological vector spaceV2.
Theorem 3.2Lets,σ>0 be such thats+σ≥1.Then the following is true:
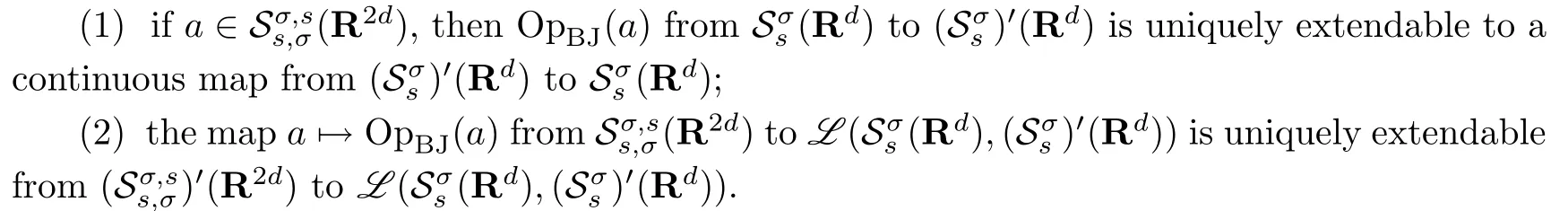

4 Born-Jordan Operators with Modulation Space Symbols

For the proof we recall that ifµandνare positive measures on measurable spaces,p,q∈(0,∞]satisfyq≤pandfisµ×νmeasurable,then Minkowski’s inequality asserts that
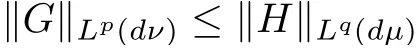
when
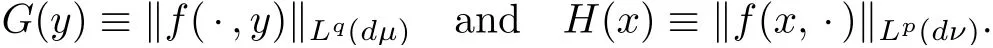
In order to treat the casep∈(0,1]in suitable ways,we need the following lemma.
Lemma 4.2Lety∈Rd,Λ⊆Rdbe a lattice andp∈(0,∞).Then
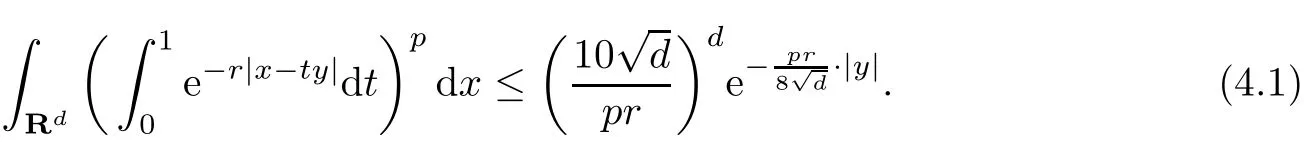
and
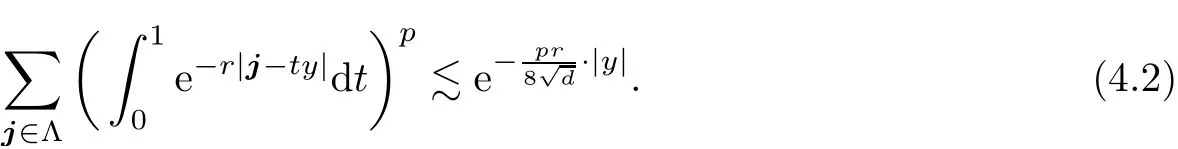
ProofIt is clear that both sides of(4.1)are even functions with respect to eachyjiny=(y1,···,yd).Hence we may assume thatyj≥0 for everyj,when proving(4.1).We prove only(4.1).The estimate(4.2)follows by similar arguments and is left for the reader.
Sinceu|→e−ruis a convex function,H¨older’s and Jensen’s inequalities give
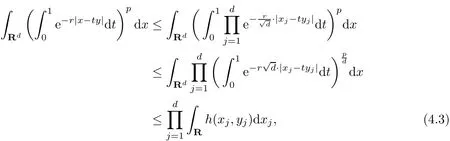
where
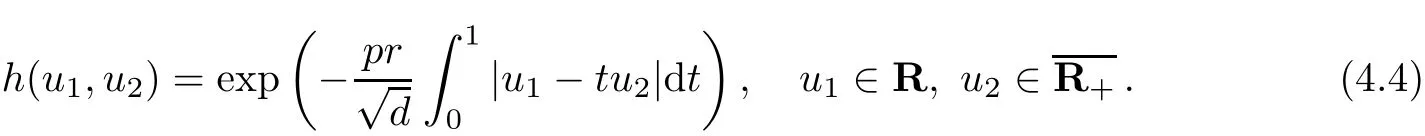
We need to evaluate the integral in(4.4).By straight-forward computations we get
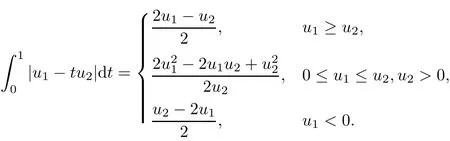
This gives
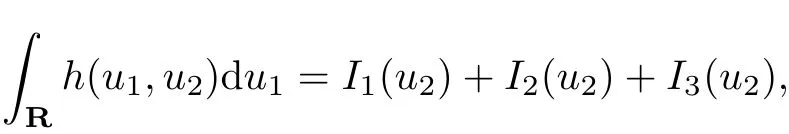
where
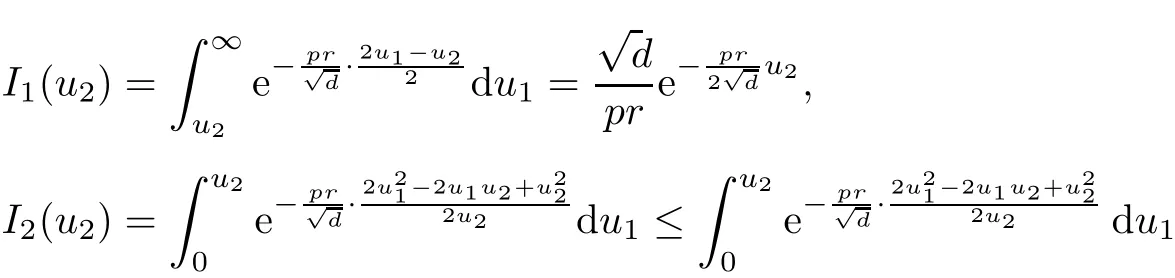



The last result in this record concerns Schatten-von Neumann properties for Born-Jordan operators when acting on modulation spaces of Hilbert type.Forp∈(0,1],the result follows from Theorem 4.5 and the fact that
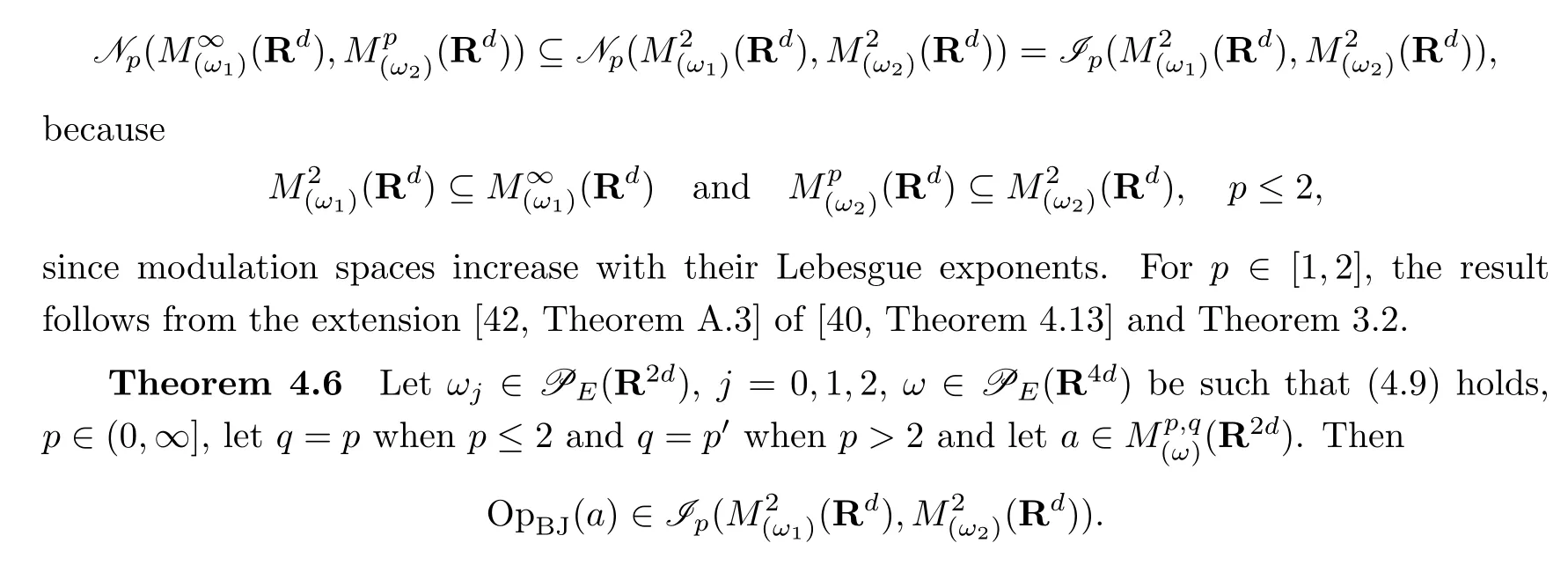
5 Born-Jordan Operators with H¨ormander Symbols
In this section we show that any Born-Jordan operator with symbol in a suitable H¨ormander class is a pseudo-differential operator with symbol in the same class.Furthermore,we deduce Schatten-von Neumann properties and lower bound estimates for such operators.Especially we deduce Feffermann-Phong’s inequality for Born-Jordan operators.


For the proof we need the following proposition.We omit the proof,since the result is essentially a restatement of Proposition 18.5.10 in[30].
Proposition 5.3Letgbe strongly feasible and split metric onR2d,mbeg-feasible,I⊆Rbe bounded,N>0 be an integer,a∈S(m,g),and letat∈S′(R2d)be such that

which gives(5.1).The proof is complete.
Theorem 5.2 shows that several continuity properties in the Weyl calculus in Chapter XVIII in[30]carry over to Born-Jordan operators.For example,the following results are immediate consequences of Propositions 18.6.2 and 18.6.3 in[30],and Theorem 5.2.
Theorem 5.4Letgbe strongly feasible and split metric onR2d,mbeg-feasible,and leta∈S(m,g).Then OpBJ(a)is continuous on S(Rd)and is uniquely extendable to a continuous operator on S′(Rd).
Proposition 5.5Letgbe strongly feasible and split metric onR2d,and leta∈S(1,g).Then OpBJ(a)is continuous onL2(Rd).
The following two theorems extend the previous result.Here and in what follows we letbe the set of allf∈L∞(Rd)vanishing at infinity,i.e.,fshould satisfy
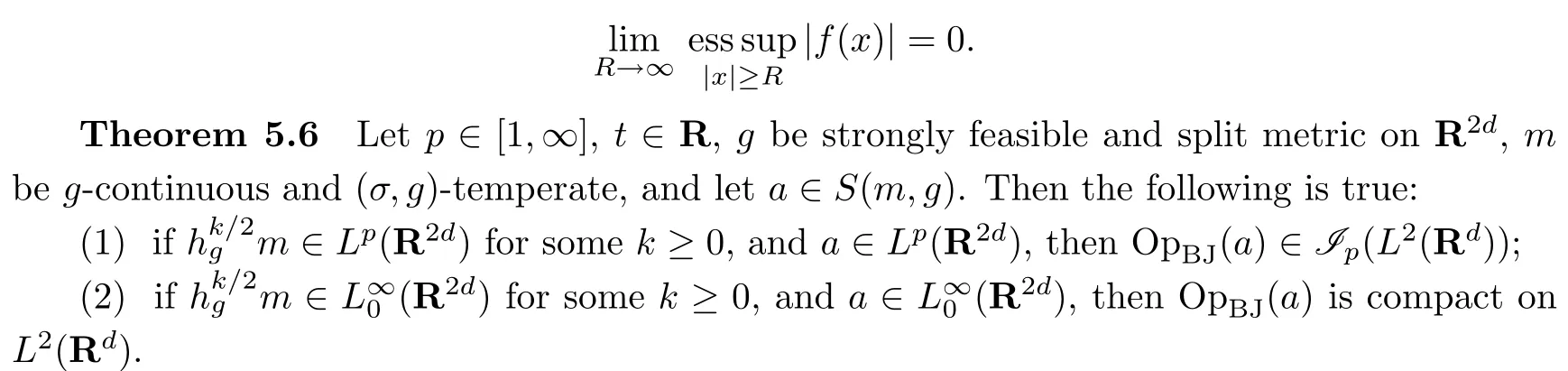
Theorem 5.7Letp∈(0,∞],t∈R,gbe strongly feasible and split metric onR2d,mbeg-continuous and(σ,g)-temperate,and leta∈S(m,g).Then the following is true:
(1)ifm∈Lp(R2d),then OpBJ(a)∈Ip(L2(Rd));
(2)ifmthen OpBJ(a)is compact onL2(Rd).
For the proof of Theorem 5.6 we need the following result which is a slight extension of[8,Proposition 2.10].The proof is omitted,since the result follows by the arguments in the proof of[8,Proposition 2.10].

Proof of Theorem 5.7The result is a special case of Theorem 4.6 in the casep≥1.If insteadp<1,then the result follows by combining[45,Theorem 4.1]with Theorem 5.2.
Finally we also have the following Feffermann-Phong’s inequality for Born-Jordan operators,which in particular shows that Sharp-G˚arding’s inequality is also true for such operators.
Theorem 5.9Letgbe strongly feasible and split metric onR2d,and let 0≤a∈Then OpBJ(a)≥−Cfor some constantC≥0.
ProofBy lettingbbe defined by Opw(b)=OpBJ(a)choosingN=2 in Theorem 5.2,it follows thatb=a+c,wherec∈S(1,g).The result now follows from the facts that Opw(a)is lower bounded onL2by the Feffermann-Phong’s inequality for Weyl operators(cf.[30,Theorem 18.6.8]),and the fact that Opw(c)is bounded onL2in view of[30,Proposition 18.6.3].
Remark 5.10By similar arguments as in the proof of Proposition 5.9,it follows that H¨ormander’s improvement of Melin’s inequality given in Theorem 6.2 in[28],holds true with Born-Jordan operators in place of Weyl operators.That is,ifgis strongly feasible and split metric onR2dandasatisfies the same conditions as in Theorem 6.2 in[28],then OpBJ(a)is bounded from below.(See also the introduction.)
Remark 5.11In[6],Bony and Chemin introduced a broad family of Sobolev type spaces,where each spaceH(m0,g)is a Hilbert space and depends on the choice of the strongly feasible metricgand theg-feasible weightm0.By Th´eor`eme 4.5 and Corollaire 6.6 in[6]it follows thatH(1,g)=L2and that there area∈S(m0,g)andb∈S(1/m0,g)such that corresponding pseudo-differential operators are inverses to each others and liftH(m·m0,g)andH(m/m0,g),respectively,toH(m,g).That is,
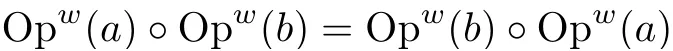
equals to the identity operator on S′(Rd)and
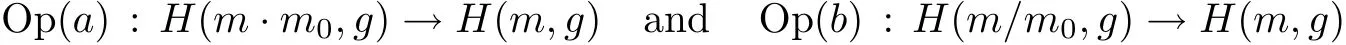
are bijections for everyg-feasible weightm.
From these results it follows that Theorems 5.6,5.7 and 5.9 can be generalized to involveH(m,g)spaces.For example,it follows from these results and Proposition 5.5 that ifgis a strongly feasible and split metric onR2d,mandm0areg-feasible,anda∈S(m0,g).Then OpBJ(a)is continuous fromH(m0,g)toH(m0/m,g).
Remark 5.12Evidently,all continuity and compactness results above applies on the symbol classes in Remark 5.1.For example,ifais symbol in a SG-class or Shubin class and belongs toLp(R2d)for somep∈[1,∞],then Theorem 5.7 shows that OpBJ(a)∈Ip(L2(Rd)).
6 Born-Jordan Operators of Infinite Orders
In this section we consider Born-Jordan operators with symbols belonging to classes considered in[9],or more generally,classes considered in[1].This means that the symbols obey ultra-regularity conditions(i.e.,certain types of Gevrey regularity),but are allowed to grow superexponentially.In particular,they are allowed to grow faster than polynomials.It is proved in[1,9]that corresponding pseudo-differential operators are continuous on suitable Gelfand-Shilov spaces and their duals.Here we use(1.2)to carry over these continuity properties and to Born-Jordan operators.
The symbol classes which we shall consider are given in the following definition.
Definition 6.1Forsj,σj>0,j=1,2,h,r>0 andf∈C∞(Rd1+d2),let

杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- ASYMPTOTIC STABILITY OF A BOUNDARY LAYER AND RAREFACTION WAVE FOR THE OUTFLOW PROBLEM OF THE HEAT-CONDUCTIVE IEAL GAS WH SY*
- ON REFINEMENT OF THE COEFFICIENT INEQUALITIES FOR A SUBCLASS OF QUASI-CONVEX MPPG RL L RB*
- EXISTENCE OF SOULUTIONS FOR THE FRACTIONAL (p,q)-LAOLACIAN PROBLEMS INVOLVING A CRITICL SOBLEV EXPNN*
- RADIALLY SYMMETRIC SOLUTIONS FOR QUASILINEAR ELLIPTIC EQUATIONS INVOLVING NONHOMOGENEOUS OPERATORS IN AN ORLICZ-SOBOLEV SPACE SETTING∗
- ON VORTEX ALIGNMENT AND THE BOUNDEDNESS OF TH Lq-NORM OF VIRUICITY IN INCOMPRESSBLE VU FUD*
- SPECTRA OF COMPOSITION GROUPS ON THE WEIGHTED DIRICHLET SPACE OF THE UPPER HALF-PLANE∗
