非等间距改进加权GM(1,1)模型在基坑变形监测中的应用

张 东，杨 静,葛继空

(1.诚邦测绘信息科技(浙江)有限公司，浙江 宁波 315000；2.中国水利水电第八工程局有限公司科研设计院，湖南 长沙 410000)

随着社会经济的发展，众多大型基础设施建设不断涌现，这些基础建设都伴随着基坑工程。基坑的开挖深度越深，技术难度也就越高，在开挖过程中，土体卸荷使受力平衡遭到破坏，导致基坑施工变形对城市周边环境影响日益突出，因此，对基坑变形实时有效监控是基坑工程成败的关键[1]。此外在施工过程中会受到施工因素、环境因素和时间因素的影响，给基坑变形预测带来一些困难[2]。由于地铁、建筑物等的众多基坑工程位于人口密集区域，一旦发生事故会造成严重后果，因此，对基坑变形预测的研究显得尤为重要。

近年来，众多变形监测研究学者对基坑监测做了大量研究，其主要应用建模方法有回归分析、时间序列分析、BP神经网络、支持向量机等[3-5]。以上研究方法通常需要的样本很大，且特点为典型概率分布，在实际工程监测应用中很难实现，因此，一定程度上限制了应用范围。灰色模型针对小样本数据处理具有一定的优越性，其GM(1,1)模型在工程领域应用最为广泛，模型大多数是基于等时间间隔的数列，而在实际工程中受环境等多方面因素影响，监测数据很难做到等时间间隔。因此，建立非等间隔GM(1,1)模型在监测应用上具有很大的实用价值。廖展宇等[6]在非等间距模型中引入等时间差系数，对差值进行分析后序列还原，最后将非等间隔序列转化成等间距序列，对基坑进行变形预测。李勇等[7]在非等间距模型中引入一种带有适应性的λ因子，然后对模型中的背景值进行优化改进。魏玉明等[8]和梁新美等[9]利用加权GM(1,1)模型分别对滑坡工程于深基坑进行变形预测。何为等[10]针对监测过程可能含有粗差情况，提出一种抗差加权非等时距GM(1,1)模型应用于大型建筑物沉降预测。

基坑工程监测点受基坑开挖的影响，往往会在短时间内产生较大的变形，现有的非等间距灰色模型在基坑应用中无法处理突变数据的影响，导致精度很低。本文在现有的非等间隔灰色模型基础上对时间做平滑，提出一种改进的加权非等间距GM(1,1)模型，并以实际基坑监测数据为例，对其方法进行实际应用。

1 非等间距改进加权GM(1,1)建模

1.1 灰色系统理论

灰色理论(Grey Theory)是由我国著名学者邓聚龙教授于1982年首次提出。它是基于关联空间、光滑离散函数等概念，定义了灰导数、灰微分方程，进而用离散数据建立了微分方程型的动态模型[11]。GM(1,1)模型是灰色系统理论中最为核心的内容，具有“小样本”的研究特质和简单实用的优点，模型建立只需要一个单变量的一阶微分方程。建立步骤具体如下：

(1)设有n个非负原始观测数据序列X(0)=[x(0)(1),x(0)(2)，…，x(0)(n)]，则由X(0)序列累加(1-AGO)得到序列X(1)为

X(1)=[x(1)(1),x(1)(2)，…，x(1)(n)]

(1)

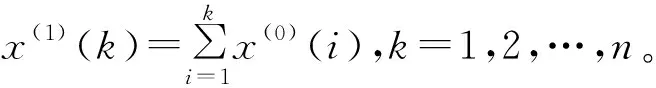
(2)由序列X(1)构造背景值序列Z(1)为

Z(1)=[z(1)(1),z(1)(2),…z(1)(n)]

(2)

式中，Z(1)取X(1)紧邻均值生成序列，即Z(1)(k)=0.5[x(1)(k)+x(1)(k-1)],k=2,3,…,n。

(3)建立灰色GM(1,1)模型的一级白化微分方程为

(3)

(4)根据最小二乘原理，灰色GM(1,1)模型的参数列为

A=[a,b]T=(BTB)-1BTY

(4)

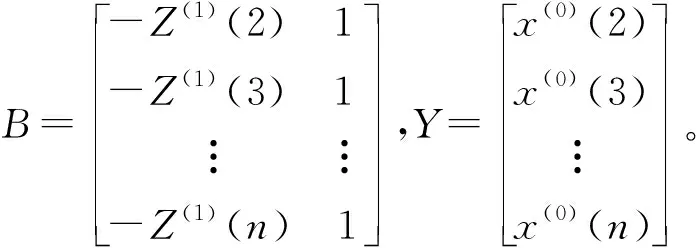
将计算求得的参数a，b带入式(3)，并求解微分方程，取初始条件x(0)(1)，得X(1)的时间响应函数为

(5)

(5)对式(5)再作一阶累减函数还原计算(1-IAGO)，得到原始序列X(0)的还原值为

(6)

1.2 非等间距改进加权GM(1,1)模型

现有非等间距GM(1,1)模型中主要是以相邻时间间隔进行加权处理，进行原始数据一次累加。现实监测过程中会受到施工扰动影响，在施工期间会受到外力作用产生较大变形，如果采用简单的加权处理这些突变数据会使残差变大，影响预测精度。 因此，本文建立非等间距改进加权GM(1,1)模型，具体建立步骤如下：

(1)设非等间距原始观测序列为

X(0)={x(0)(t1),x(0)(t2)…，x(0)(tn)}

(7)

式中，tn-tn-1≠常数；x(0)(ti)为ti时刻监测点的变形值。

(2)对原始序列做一次累加处理

(8)

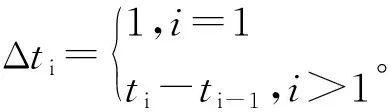
(3)对原始累加序列改进赋权处理，单位时间内变形为

(9)

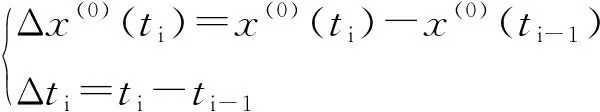
令ρi=βvi

(10)

式中，ρi为原始序列叠加权，ρ1=1;β是为了保证原始序列最大时间间隔的一致。

(11)

通过以上定权的优点在于适应基坑突变问题，当变形速率较大时，即施工期间，累加序列可以适当放宽；当变形速率较小时，即停工期间，累加序列适当压缩时间；当变形速率为负数，累计序列变小，可以认为是时间的回退。

(12)

得到序列

X(1)={x(1)(t1),x(1)(t2),…,x(1)(tn)}

(13)

(4)同理式(3)、式(4)，建立一阶微分方程，估计参数列。将求取参数代入微分方程，可得离散解

(14)

还原数据

(15)

(5)因为预测序列n+1…的ρk是未知的，需要做如下近似：

取j=1,2,…，m表示时序号，则有

(16)

还原数据

(17)

若︳ρn︳比较小，表明变形已经趋于稳定，可以把tn以后的每个时刻变形值拟合出来，即：

(18)

2 模型的精度检验

为判断非等间距改进加权GM(1,1)模型预测的可靠性，需要对模型的精度进行检验，通常是通过后验差法。本文采用相对误差、绝对误差(残差)、均方差比值C及小误差概率P四个指标来评价拟合预测效果。

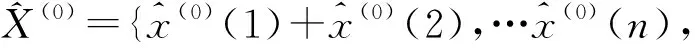
e=[e(1),e(2),…,e(n)]

(19)

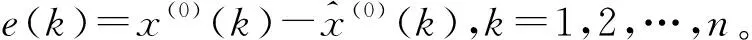
e表示拟合值、预测值与原始数据的接近程度，因此e值越小越好。

相对误差序列为：

(20)

相对误差Δ表示预测残差占原始数据的比例，因此，越小越好。

原始数列X(0)及残差数列e的方差为：

(21)

(22)

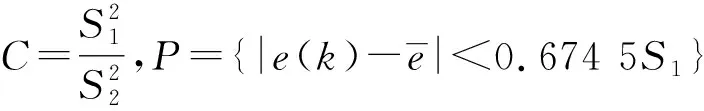
(23)

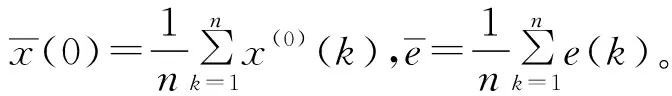
后验方差比值C和小误差概率P共同决定模型精度。C值越小则预测精度越好，P值越大说明误差较小的概率越大，模型精度越高。具体精度等级参照如表1所示。

表1 后验差检验法精度等级参照表

3 实例与分析

本文以某高速跨铁路转体桥的钻孔灌注桩基坑基础监测数据为例[12]，来验证非等间距改进加权GM(1,1)模型对基坑监测的可行性和有效性。具体监测数据如表2所示。

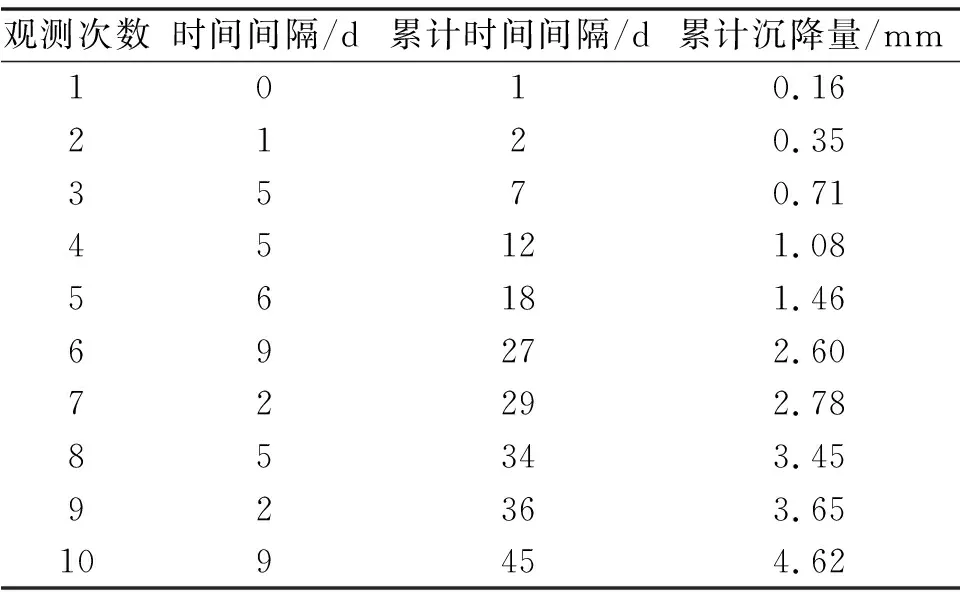
表2 基坑测点监测数据

首先，选取前7期监测数据作为原始序列分别建立传统非等间隔加权GM(1,1)模型和非等间距改进加权GM(1,1)模型，用第8～10期数据来验证预测结果，两种模型对监测数据拟合与预测结果如表3所示。

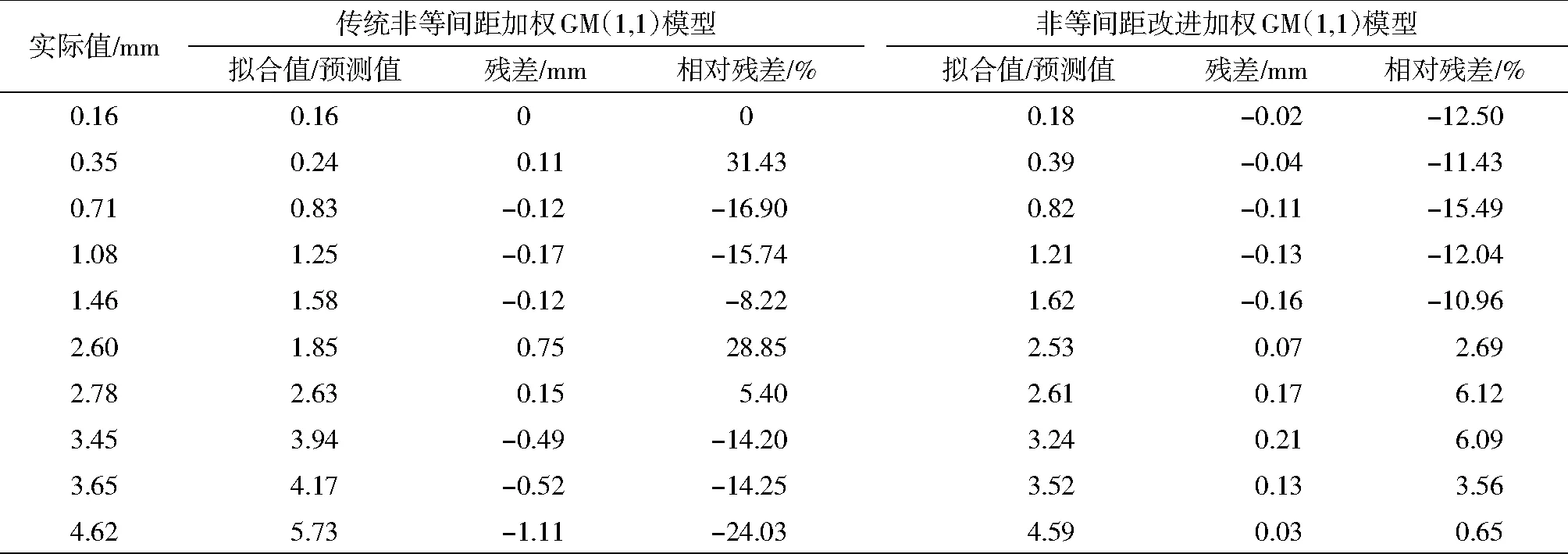
表3 监测点拟合预测结果检验表

由图1可知，非等间距加权改进GM(1,1)模型相比传统的非等间距加权GM(1,1)模型拟合预测曲线更加光滑，变化波动更小。在前5期中，传统模型与改进模型拟合精度都较高，但是随着时间推移，第6期以后出现转折，改进模型越来越接近实际值，而传统模型则离实际变形曲线偏差变大。

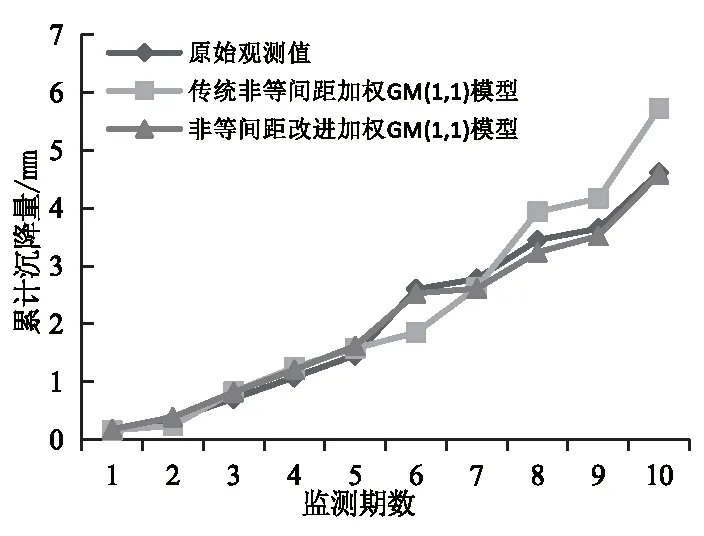
图1 实测值与拟合预测值对比图

由图2和表3可知，非等间距改进加权GM(1,1)模型相比传统的非等间距加权GM(1,1)模型残差有明显的提高，特别在第5期以后两种模型出现很大的差异。改进模型在第5期以后残差由0值以下变为0值以上，从第8期开始越来越接近0值，即残差越来越小。传统模型在第5～6期残差发生突变，由负值变为正值最高峰，第6期以后，残差变小，经过0值到达负值最高峰。

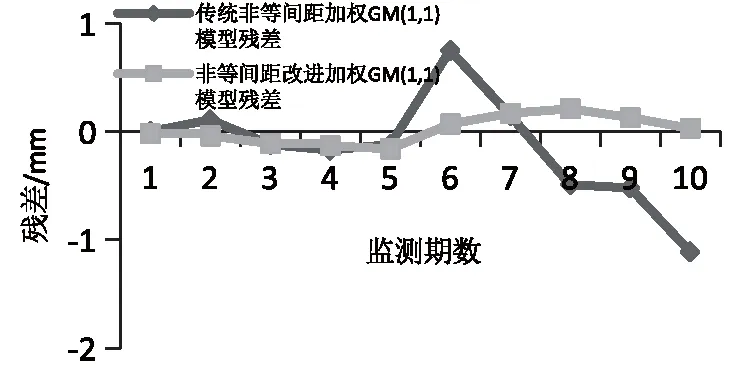
图2 两种模型残差曲线图

将两种模型进行精度对比分析，由表4可知，无论是后验差比值还是小误差概率，非等间距改进加权GM(1,1)模型都优于传统非等间距加权GM(1,1)模型，且精度等级达到1级。

表4 两种模型分别所在的精度等级

综合以上分析，若基坑变形处于不稳定状态，如基坑开挖中，传统非等间距加权GM(1,1)模型预测精度较差，而非等间距改进加权GM(1,1)模型在基坑开挖结束后，在预测下一时刻的变形时，加入上一时刻的变形预测值，去除老的信息的时刻变形值，进行重建模型，实现动态预测。

4 结 语

本文针对现有的非等间距模型在基坑监测应用中的不足，提出一种非等间距改进加权GM(1,1)模型，该模型弥补了基坑监测中动态变化预测精度低、残差大的缺点。结合具体基坑监测数据，进行建模，通过精度对比分析，结果表明，本文所述模型精度更高，在时间跨度较短区域改进加权处理动态灰色模型更加有优势，突变后变平稳时精度有所降低。综上所述，本文所述模型在基坑工程的变形处理中值得推广，对基坑监测应用有很好的实用价值。