基于改进Canny算法的噪声图像边缘检测

赵子润,高保禄,郭云云,田 力

(太原理工大学 软件学院，太原 030024)

0 引言

边缘检测[1-2]是图像处理的基本操作，边缘检测的质量直接决定高级图像处理的性能。在过去十几年中，已经提出了数百种用于数字图像中的边缘检测的方法。根据边缘检测器所基于的原理，可以将其分类为基于分化的方法[3]、统计方法[4]、机器学习方法[5]、主动轮廓法[6]、多尺度方法[7-8]，以及各向异性扩散方法[9-10]等。Canny算法[11]相比于其他的边缘检测算法具有较高的性能。但是经典算法采用线性的高斯滤波器对图像进行平滑，并从整体上对图像进行模糊，没有考虑像素间的相似程度，使得去噪效果不好且精度下降，同时对双阈值的选取是依据人的经验预先确定，导致检测结果丢失边缘或者检测出虚假边缘。

针对Canny算法存在的问题，研究者提出了许多的改进算法。文献[12]提出基于双边滤波的Canny算法，该算法同时考虑了图像的空间信息和灰度信息，提升了低浓度含噪图像的边缘检测效果，但对于较高浓度含噪图像的检测效果不佳。文献[13]采用了预定义尺度的各向同性高斯核对Canny算法进行优化，但该算法产生了边缘检测和定位精度之间的二重性，导致噪声无法被有效去除。文献[14]提出基于偏微分方程的方法，该方法对含有低浓度噪声图像的边缘检测效果清晰，但由于平滑图像时进行迭代操作比较复杂，因此随着噪声浓度的提高，检测到的边缘很快变得模糊。文献[15]提出了尺度不变和对比度不变的多尺度差分边缘检测器，噪声被过滤为低对比度特征后能够准确地提取边缘特征，但它只对几种退化的真实世界图像数据集进行了实验，缺乏普适性。文献[16]提出基于曲率估计的检测算法，在小尺度高斯核的Canny算法中引进曲度算子对图像卷积，然后再利用大尺度高斯核对卷积图像进行修正，但两次计算仍然采用预定义尺度的高斯滤波器，无法适应图像本身的特征，导致一些噪声不能有效地剔除。

综上所述，本文提出了基于改进Canny算法的噪声图像边缘检测方法，通过构建自适应高斯滤波器改进了曲度算子，使图像的局部平滑效果达到最佳，得到优化的二值边缘图；在双阈值选取上，基于最大类间方差法，充分考虑图像的灰度信息与梯度信息构造了灰度梯度映射函数，获得最佳双阈值，进行双阈值检测以及边缘连接。实验结果表明，该算法在有效去噪的同时，所提取的边缘更加清晰准确，并且具有自适应性强和算法效率高的优点。

1 传统Canny边缘检测算法

传统Canny算法的实现包括以下4个步骤：1)对图像进行高斯平滑滤波；2)对平滑后的图像I(x,y)计算梯度强度和方向；3)使用非极大值抑制操作，保留邻域内最大梯度强度值，且对其他梯度强度值进行抑制。抑制结果为M；4)使用高低双阀值(高阀值Thmax和低阀值Thmin)检测边缘像素。

郑子华等人[16]提出基于曲率估计的 Canny 边缘检测算法(简称曲率估计算法)，该算法中定义了边缘曲度算子CURV，算法的处理过程如下：

1)计算高斯滤波函数，如式(1)所示，取σ=2，得到原始图像边缘图，记为Kmax。

(1)

2)取σ=1，得到原始图像边缘图，记为Kmin。

3)对Kmin求取CURV，并利用Kmax对CURV进行修正。

4)根据K=M-CURV得到更新后的边缘图K。

5)根据人工设置的双阈值对K进行边缘判断，得到边缘检测结果。

以上的算法流程中分别使用两个空间尺度的高斯滤波器得到边缘图。但两次计算的空间尺度系数都是根据经验选择的常用值，没有根据图像局部特征进行降噪，使得降噪效果不佳，自适应性不好。算法结果如图1所示。

图1 加入椒盐噪声的检测结果

2 改进Canny边缘检测算法

本文在郑等人的基础上作了两方面的改进:1)构建自适应高斯滤波器，改进了曲度算子，对噪声图像进行降噪；2)基于最大类间方差法又引入了图像的梯度信息，进而构造了灰度梯度映射函数获取最佳双阈值。

2.1 自适应高斯滤波器的曲度算子

2.1.1 构建的自适应高斯滤波器

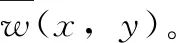
(2)

用当前像素灰度值与窗口的平均值作差得到σ，计算以下3种情况的σ值。

1)当像素点位于非边缘区时，筛选器窗口中的灰度值相差不大，σ值由式(3)所示:

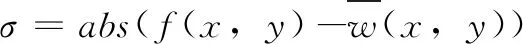
(3)

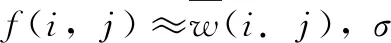
2)当像素点是图像的边缘时，根据边缘的连续性，筛选器窗口中至少有3个点属于边缘。设非边缘点为f(x-1,y-1)。σ值由式(4)所示：

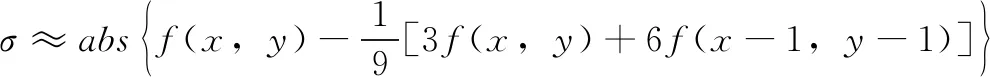
(4)

计算得到的σ值仍然是较小的，由于实际的滤波器窗口中经常多于3个边缘像素点，计算后得到的σ值会更小。

3)当像素点是图像中的噪声点时，σ值由式(5)所示：

abs{f(x,y)-f(x-1,y-1)}

(5)

此时得到的σ值比较大。

根据式(6)和式(7)计算高斯函数在x和y方向上的一阶偏导。

(6)

(7)

用二维的高斯函数对整个图像滤波，并分析σ值。在非边缘区域时，σ值接近0，滤波器只做简单平滑处理；在边缘上时，σ值比较小，边缘被识别并保留；对于噪声像素点，由于它是孤立的，所以σ值很大。经过滤波后，σ值很大像素点音被剔除。

通过上述步骤方法实现自适应的高斯滤波，能够针对图像本身特点进行平滑和降噪。

2.1.2 计算边缘像素的曲度算子CURV

1)梯度方向θ(x,y)对应二值边缘图K中的点K(x,y)，以K(x,y)为中心中取5×5的邻域。

2)取x-2≤p≤x+2，y-2≤q≤y+2，遍历5×5邻域中的点K(p,q)，记α(p,q)为过K(x,y)与过K(p,q)的两切线的夹角。

当K(p,q)=0时，K(p,q)为非边缘点，α(p,q)=0；

当K(p,q)=1时，K(p,q)为边缘点，令:

θ1(p,q)=|θ(x,y)-θ(p,q)|

(8)

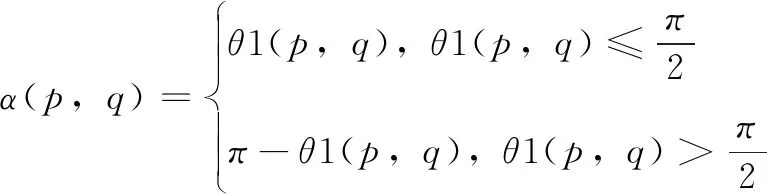
(9)

其中:梯度方向θ(x,y)是 Canny 算法的中间结果。

3)计算CURV(x,y)。

(10)

其中:N是K(x,y)邻域中边缘点个数。

通过基于改进的自适应高斯滤波器计算曲度算子，实现图像的降噪工作，但在双阈值检测及连接边缘的阶段中，双阈值的选取是根据经验设置的，固定的双阈值不能充分考虑每幅图像所特有的像素特征，导致边缘丢失或虚假边缘被检出。对此，本提出灰度梯度映射函数的双阈值选取方法。

2.2 灰度梯度映射函数的双阈值选取

在双阈值的选取上很多研究者引入了最大类间方差法[17]，它是一种简单便捷的自动阈值选取方法。但是最大类间方差法仅采用灰度均值表示阈值，这会导致有偏的差估计结果。而图像梯度能很好地反映图像的边缘信息，因此将梯度引入最大类间方差法中，能弥补单一灰度信息造成的阈值偏差。

本文结合了图像的灰度特征与梯度信息，提出基于最大类间方差法的灰度梯度映射函数获取最佳阈值的方法。过程如下：

2.2.1 计算最大类间方差法判别式

设一幅图像的L个灰度级[1,2,，L]。灰度级为i的像素数为ni，则像素总数为N=n1+n2++nL。根据阈值t，图像分为两部分：背景和目标，即C0=[1,2,t]和C1=[1,2,,L]。那么每个灰度级i出现的概率为：

(11)

总均值为：

(12)

C0和C1的概率和均值为：

(13)

(14)

(15)

(16)

最大类间方差法判别式如下：

(17)

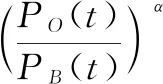
2.2.2 计算基于Canny算法的梯度函数

Canny算法的中间结果包含梯度值，本文用C(x,y)表示该梯度值。梯度函数由下式得到：

(18)

其中:Ri表示像素的集合Ri={(x,y)|f(x,y)=i}，T(i)表示灰度值为i时对应的平均梯度值。

2.2.3 构造灰度梯度映射函数

两种函数进行指数形式的融合调节效果最明显，在此处，即表明对边缘的判别和检出效果更好。

由此，本文构造的灰度梯度映射函数如下：

J1(t)=(J(t))T(i)

(19)

2.2.4 计算最佳阈值

以此得到的最佳分割阈值为：

(20)

通过以上方法获得的最佳阈值为高阈值，根据双阈值判定的步骤可知，当被判别的像素点梯度强度值大于高阀值时，则确定为边缘点，由于这里选取的为最佳阈值，因此仅通过这一次判别，便可在最大范围内判定大部分的边缘点。高低阈值的设定，两者通常为二倍或三倍的关系，获得的最佳分割阈值已使大部分边缘点被确定，因此本文采用二倍关系选取低阈值。

2.3 本文算法流程

该算法完整的步骤描述如下：

1)首先根据第2.1节自适应高斯滤波器运算得到优化的二值边缘图K，并保留梯度值的计算结果C(x,y)以及非极大值抑制后的计算结果M；

2)根据第2.1节改进的曲度算子的计算步骤，对K求取CURV；

3)更新K值，K=M-CURV；

4)根据第2.2节中算法步骤构造灰度梯度映射函数，设置双阈值；

5)对K进行判断；

6)进行边缘连接，完成检测。

本文详细的算法步骤如图2所示。

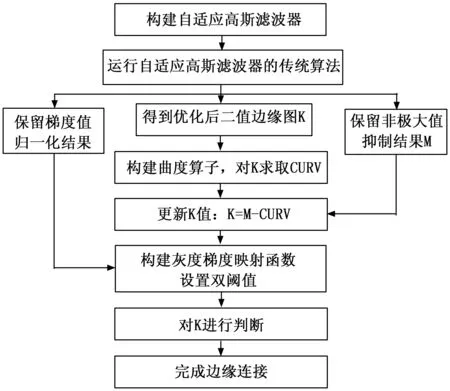
图2 本文算法步骤图

3 实验结果与分析

本文进行实验的平台配置为：Intel 2.6 GHz CPU、4 GB 内存、Microsoft Windows7 64位操作系统，在 Matlab R2017a 软件下进行实验。选取了BSDS500自然图像数据集，本文在该数据集上进行了广泛的实验和评估，从定性和定量两个方面分析对比了本文算法、传统Canny算法以及曲率估计算法的性能。实验结果如下。

3.1 定性分析

3.1.1 不同类型噪声环境下的边缘检测

图3中选取了3幅图片，分别对原图像3(a)加入浓度较低的高斯白噪声，所得噪声图如图3(b)所示。固定空间尺度系数σ=1，通过传统Canny算法对噪声图的边缘检测结果如图3(c)所示，通过本文的改进算法对噪声图进行边缘检测的结果如图3(d)所示。

图3 加高斯白噪声的实验结果比较

图4中选取相同的3幅图片，分别对原图像4(a)加入浓度较低的椒盐噪声，所得噪声图如图4(b)所示。固定空间尺度系数σ=1，通过传统Canny算法对噪声图的边缘检测结果如图4(c)所示，通过本文的改进算法对噪声图进行边缘检测的结果如图4(d)所示。

图4 加椒盐噪声的实验结果比较

从图3和图4边缘检测结果观察得出，本文的改进算法对高斯白噪声图和椒盐噪声图，均检测出清晰连贯的边缘，很好地抑制了噪声。例如图3(d)和图4(d)中人物面部的眼窝、嘴巴和手指部分的边缘被完整保留，建筑物的棱角和圆顶部分的边缘清晰；而传统Canny算法对高斯白噪声图和椒盐噪声图的处理，噪声与图像的边缘轮廓混合到一起，边缘被噪声淹没，无法确认有效的边缘。综上所述，本文算法性能极大的优于传统Canny算法。

3.1.2 同一噪声在不同浓度下的边缘检测

为进一步验证在较高浓度噪声下本文算法的优势，实验中选择椒盐噪声，然后设置不同的浓度加入原图像，获得噪声图。与曲率估计算法比较，实验结果如图5所示。

图5 浓度为0.02椒盐噪声环境下的实验结果比较

图6 浓度为0.1椒盐噪声环境下的实验结果比较

图7 浓度为0.2椒盐噪声环境下的实验结果比较

图5、图6和图7依次对人物图片加入不同浓度的椒盐噪声后，曲率估计算法与本文算法的实验结果比较。图5(b)为加入浓度0.02的噪声图，曲率估计算法的边缘检测如图5(c)所示，本文算法的边缘检测如图5(d)所示。两者的检测结果均比较理想，但是，曲率估计算法会检测出错误的边缘细节信息，并且检测出来的线条较粗、不平滑；图6(b)为加入浓度0.1的噪声图，曲率估计算法检测结果如图6(c)所示，开始出现了变异，特别是人物袖口和肩部出现噪声点，影响了正确边缘的检测，本文算法的检测结果如图6(d)所示，边缘的检测依旧保持稳定，没有出现噪声干扰正确边缘的情况；图7(b)为加入浓度0.2的噪声图，由于噪声浓度高，曲率估计算法的检测结果如图7(c)所示，噪声点分布密集，与正确边缘混合在一起，导致边缘淹没在噪声中，很难辨认有效边缘，而本文算法的检测结果如图7(d)所示，边缘仍然比较连贯，尽管有噪声被标出，但没有影响正确边缘的确认。

3.2 定量分析

3.2.1 均方误差和图像峰值信噪比的定义

对于图像质量的量化评价指标通常是均方误差(MSE，mean squared error)MSE和峰值信噪比(PSNR，peak signal to noise ratio)PSNR。MSE和PSNR均表示两幅图像的相似程度。在本文中MSE的值越小，表示对噪声图像的降噪效果越好。MSE的定义如下：

(21)

PSNR的定义如下：

(22)

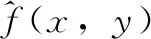
3.2.2 各算法MSE值和PSNR值的比较

表1是传统Canny算法、曲率估计算法与本文算法的MSE值、PSNR值比较。

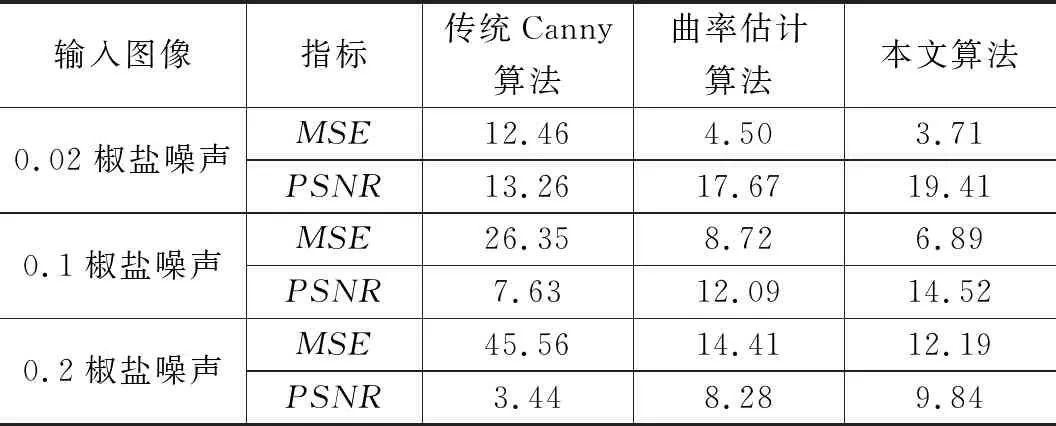
表1 各算法检测结果的MSE值、PSNR值比较

从表1中得出，本文算法在三种情况下都有最小的MSE值和最大的PSNR值，相比于曲率估计的算法，PSNR值平均提高了1.9%，MSE值平均降低了1.6%。

本文算法构造自适应高斯滤波器改进了曲度算子，得到了优化的边缘图，在双阈值的选取上，基于最大类间方差法构建了灰度梯度映射函数，确定了最佳的双阈值。比曲率估计算法中固定的空间尺度系数和人工选取的双阈值能更好地适应图像本身特征，因此本文算法降低了MSE值，提高了PSNR值。

3.2.3 各算法运行时间的对比

表2对比了传统Canny算法、曲率估计算法与本文算法的运行时间。分析表2得到，本文算法在0.02高斯白噪声、0.02椒盐噪声、0.1椒盐噪声和0.2椒盐噪声4种情况下运行的时间均比曲率估计算法运行时间短。由于曲率估计算法在降噪后，又采用大尺度空间系数的计算修正小尺度下的结果，两次计算使得运行时间增长一倍多。由于本文对双阈值选取的过程也进行了改进，而其中含有迭代计算，使得本文算法总运行时间略长于传统Canny算法，两者基本接近，能很好地满足有实时性要求的应用场景。综上所述，定量分析的结果与定性分析结果一致，充分表明本文算法的优越性。

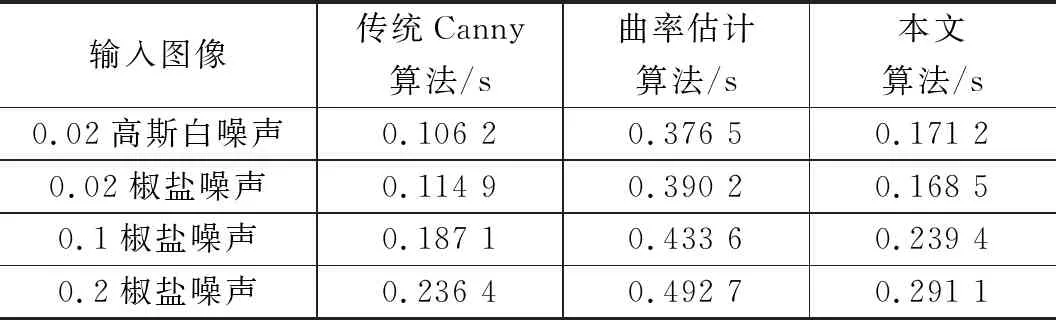
表2 3种算法在不同情况下的运行时间

4 结束语

本文针对传统Canny边缘检测算法对噪声图像的去噪效果不佳，以及双阈值需要预先设定的问题，提出了一种基于改进Canny算法的噪声图像的边缘检测。首先构建自适应的高斯滤波器对曲度算子进行改进，得到优化的二值边缘图；然后在双阈值选取上，基于最大类间方差法构建了灰度梯度映射函数，确定了最佳的双阈值；最后对二值边缘图进行双阈值检测和边缘连接，从而实现对图像的边缘特征提取。

从定性和定量两方面的对比实验表明，本文算法很好地解决了传统Canny算法对噪声图像的去噪效果不佳，以及固定的双阈值的问题，保存了连续完整的轮廓边缘，算法的运行效率也较高。然而，本文算法也存在一些不足，在最大类间方差法的判别式中指数参数α的确定是一个问题，它的选取还可以进行更具体化的改进；另一个是针对边缘提取的细节部分，比如图像中角点部分的连接效果不佳，存在断裂。今后的工作将在此基础上进一步研究解决这两个问题。